Gottstein G., Shvindlerman L.S. Grain Boundary Migration in Metals: Thermodynamics, Kinetics, Applications

Подождите немного. Документ загружается.

324 3 Grain Boundary Motion

ΙΙ

ΙΙΙ

ΙΙ

ΙΙΙ

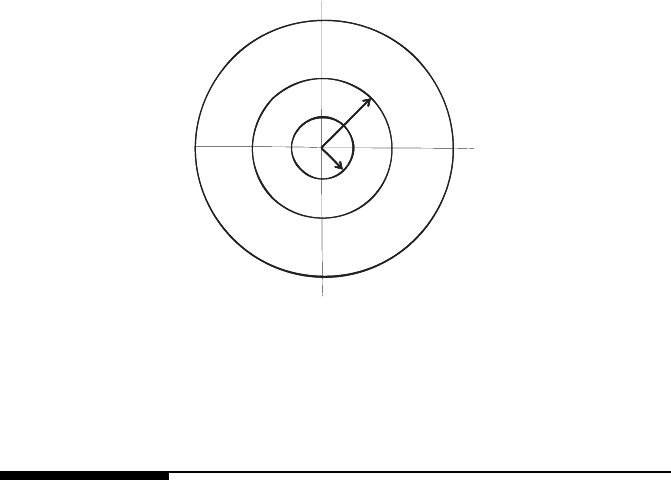
FIGURE 3.137

Cylindrical tricrystal of Al under hydrostatic pressure at 500

◦

3.9 Problems

PROBLEM 3.1

Evaluate the driving force of grain growth in a sample with boundary excess

volume V

under hydrostatic pressure P .

PROBLEM 3.2

A hydrostatic pressure 10

Pa (∼ 10

atm) is applied to an Al cylindrical

specimen at 500

◦

C (see Fig. 3.137).

The grain boundary excess free volume of the grain boundary GB

is equal

to 1.4 ·10

−10

, of the grain boundary GB

=0.6 ·10

−10

,re-

spectively. The mobility of grain boundaries GB

and GB

under atmospheric

pressure are: m

= m

=2· 10

−6

/J.s. The activation volume of grain

boundary migration is equal to V

=10

−5

/mol for both grain boundaries

(Eq. 3.159).

Calculate the time when the grain II will disappear, in other words, the

time when grain boundary GB

will catch the boundary GB

PROBLEM 3.3

Solve Problem 3.2 for the case that the grains are spheres. The values of all

other parameters remain unchanged.

PROBLEM 3.4

Determine the driving force for grain boundary migration in a polycrystal

3.9 Problems 325

Direction of

the motion

Grain

boundary

Rotation

axis

Direction of

the motion

Grain

boundary

Rotation

axis

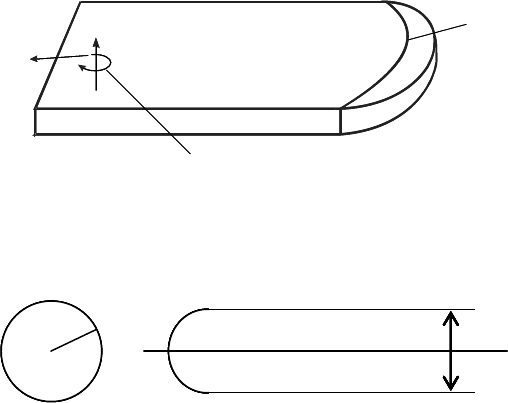
FIGURE 3.138

A turbine blade with a grain boundary during angular motion.

(a) (b)

FIGURE 3.139

Circular grain (a) and grain boundary half-loop (b).

(e.g. turbine blade) during angular motion (Fig. 3.138).

PROBLEM 3.5

Compare the rate of reduction of the surface free energy for two 2D conﬁgu-

rations: a circle with radius R and a half-loop of the size a = R (see Fig. 3.9).

PROBLEM 3.6

Use the so-called weighted mean curvature approach to determine the driving

force for grain boundary motion of the following conﬁgurations:

(1) a circular cylinder of radius R;

(2) a sphere of radius R;

(3) a grain boundary quarter-loop;

(4) a grain boundary system with triple junctions;

(5) a 2D regular n-sided polygon under junction kinetics. How does the driv-

ing force change with the topological class n of the grain?

Hint: Grains in a 2D system at junction kinetics are bordered by straight lines

and tend to form regular polygons.

PROBLEM 3.7

(a) Derive the L¨ucke-Detert relation for grain boundary motion in a system

with impurities in the case of negative adsorption.

326 3 Grain Boundary Motion

(b) Examine when the system satisﬁes the principle of maximal rate of free

energy reduction.

PROBLEM 3.8

Consider the eﬀect of grain boundary detachment of a 38

◦

111 tilt grain

boundary from impurities in Al bicrystals. The driving force for grain bound-

ary motion is 6·10

J/m

; the concentration of impurities (at. %): Si = 1·10

−5

;

Zn = 1 · 10

−5

;P< 3 · 10

−4

;Cu=7· 10

−5

;Ti< 3 · 10

−6

;K=1· 10

−4

;Cl

=1· 10

−4

. The temperature dependence of grain boundary mobility is given

in Fig. 3.70.

Use the L¨ucke-Detert, Cahn, L¨ucke-St¨uwe approaches to ﬁnd:

(1) the impurity which dominates solute drag;

(2) the diﬀusion characteristics of this impurity;

(3) the kinetic properties of the grain boundary;

(4) the adsorption characteristics of the grain boundary and the impurities.

PROBLEM 3.9

Consider grain growth in a system with mobile particles. The radius of the

particles is r, the volume fraction of the particles is c.Thenumberofthe

particles is constant and the particles are distributed uniformly in the bulk of

the sample.

(1) Derive an expression for the grain growth kinetics when the grain bound-

ary sweeps up the particles during its motion.

(2) Calculate the time dependency of the mean grain radius.

PROBLEM 3.10

Estimate the eﬃciency of retardation of grain growth in an Al polycrystal

at 673 K by mobile particles. The radius of the particles r = 50 nm, grain

boundary mobility at 673 K m

=2·10

−12

/J·s, γ =0.5J/m

.Thevolume

fraction of the particles is c =10

−4

PROBLEM 3.11

Consider a polycrystal with mobile second-phase particles. Show that there is

a certain radius of the particles which makes the particle drag most eﬃcient.

Hint: Consider a single size particle distribution.

PROBLEM 3.12

Consider three grain boundaries with the following activation parameters of

grain boundary migration [404]:

Grain Boundary I (GBI): H =1.4eV,A

=10

Grain Boundary II (GBII): H =2.2eV,A

=10

Grain Boundary III (GBIII): H =1.67 eV, A

=10

/s (1) Prove that the

compensation plots of all three grain boundaries intersect in one point.

(2) Determine the compensation temperature of this system.

(3) Calculate the ratio of the grain boundary mobilities at 380

◦

C and 520

◦

3.9 Problems 327

PROBLEM 3.13

Consider the migration of a grain boundary in a magnetic ﬁeld as the motion

of an electric conductor. This causes an electromotive force, i.e. generates a

drag force on the grain boundary. The change of grain boundary mobility m

can be described as

Δm

σv



(3.234)

where σ is the conductivity,  is the thickness (or the width) of the sample, c

is the speed of light, v is the velocity of grain boundary motion.

Find the time dependency of the mean grain size of a polycrystal during

grain growth in a magnetic ﬁeld.

Thermodynamics and Kinetics of Connected

Grain Boundaries

“... You’re the only one who seems to understand

about tails. They don’t think — that’s what’s the

matter with some of these others. They’re no

imagination. A tail isn’t a tail to them, it’s just a

Little Bit Extra at the back.”

— A.A. Milne

“Expediency, therefore, concurs with Nature in stamping

the seal of its approval upon Regularity of conformation;

nor has the Law been backward in seconding their eﬀorts.

‘Irregularity of Figure’ means with us the same as,

or more than, a combination of moral and criminality with you,

and is treated accordingly.”

— Edwin A. Abbott

4.1 Microstructural Elements of Polycrystals

The major elements of a polycrystalline structure are grain boundaries. The

energy of these grain boundaries is the source of the driving force of grain

growth; their motion and interaction either mutually or with crystal disloca-

tions constitute the mechanisms of recrystallization. The main properties of

the boundaries, which are essential for the migration process, are the surface

tension γ and mobility m

. As repeatedly mentioned, these properties are

likely to diﬀer for diﬀerent grain boundaries. Furthermore, grain boundary

surface tension and mobility can depend on the boundary orientation (incli-

nation). The motion of a grain boundary segment is determined by the grain

boundary shape in its closer vicinity.

In the course of motion grain boundaries interact with other grain bound-

aries. These interactions occur along the lines of intersection of grain bound-

aries, which are called triple junctions (Fig. 4.1). Besides grain boundaries and

triple junctions there is only one more topological element of a 3D arrangement

329

330 4 Thermodynamics and Kinetics of Connected Grain Boundaries

triple line

quadruple

point

grain boundary

triple line

quadruple

point

grain boundary

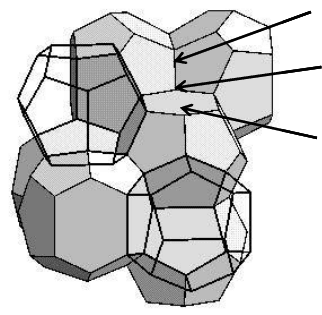
FIGURE 4.1

Grain structure with grain boundary triple lines and quadruple points.

of connected boundaries, a grain boundary quadruple point at the location

where four grains meet. At the same time this point is the location where

four grain boundary triple lines intersect (Fig. 4.1). There is a large variety

of potential triple lines and quadruple junctions in polycrystalline materials

since their geometry is determined by the constituting grain boundaries, each

of which has ﬁve degrees of freedom. Hence, a triple line is deﬁned by 12 in-

dependent geometrical parameters; a quadruple point requires 21 quantities

for a unique geometrical characterization. Six grain boundaries, four grains

and four triple junctions meet in one quadruple point (junction). All other

intersections are energetically unproﬁtable and as a consequence unstable.

These junctions possess speciﬁc physical properties (line tension γ



[1, 400,

402], triple junction and quadruple point mobility m

and m

[403]) and

move under the action of the surface tension of grain boundaries which join

at the junction and, in the case of triple lines, by their own line tension [401].

In the context of triple junctions we will consider only the intersection

of three boundaries. It is obvious that a line of intersection of two bound-

aries does not make sense physically. More than three boundaries might, in

principle, intersect along one line; however, such conﬁguration is energetically

unproﬁtable and splits into several triple junctions. More than three grain

boundaries do not intersect along a line, but can meet in one point, the so-

called quadruple point or quadruple junction of grain boundaries.

4.2 Thermodynamics of Triple Junctions 331

4.2 Thermodynamics of Triple Junctions

The thermodynamics of triple junctions might be treated in analogy to Gibbs’

thermodynamics of interfaces. We may here remark that a nearer approxima-

tion in the theory of equilibrium and stability might be attained by taking

special account, in our general equations, of the lines in which surfaces of

discontinuity meet. These lines might be treated in a manner entirely anal-

ogous to that in which we have treated surfaces of discontinuity. We might

recognize linear densities of energy, of entropy, and of the several substances

which occur about the line, also a certain linear tension. With respect to these

quantities and the temperature and potentials, relations would hold analogous

to those which have been demonstrated for surfaces of discontinuity ([1]). The

properties of the triple junction line can be determined formally according to

Gibbs as a diﬀerence between a real system, in which the triple junction line

is a distinct conﬁguration, connected to three boundaries (interfaces) and an

ideal system, where the structure and the properties of the three boundaries

are assumed to be unaﬀected by their line of intersection. However, gener-

ally a change in the length of a triple junction line and in the area of the

grain boundaries are rigidly connected. Therefore, changes of triple junction

and boundary extensions should be considered in conjunction. Namely, if M

is a certain extensive parameter of the system (energy, volume, etc.), then

the triple junction and the boundary part can be determined as a diﬀerence

between the total value of M and its bulk part



+ M

= M −



+ M



(4.1)

where M

+ M

= M

is the bulk part of the system, α and β are two parts

of the system, in particular, the grains; M



and M

are the triple junction

and boundary parts of the system, respectively.

In accordance with the concepts considered (Chapter 1), we assume that

not only the excess surface volume is equal to zero (V

= 0), but also the

excess triple junction volume V



is equal to zero: V

+ V

= V ,whereV is

the total volume of the system. Geometrically it means that its 3-D shape,

e.g. (column or prism) of a triple junction, is replaced by a line. In analogy to

Eq. (1.27) we obtain

M = m

+ m

A + m



 (4.2)

where m

and m

are the bulk densities, m

is the surface excess density, m



is the triple junction line excess density of the property M,

A is the area of

the boundaries (interfaces) in the system,  is the length of the triple junction

line. Let us introduce one of the most important surface and linear excesses

— the adsorption. For the i-th component in accordance with Eq. (1.28) we

obtain

= n

+ n

+Γ

A +Γ



 (4.3)

332 4 Thermodynamics and Kinetics of Connected Grain Boundaries

is the number of atoms of the i-th component, n

is the respective atomic

densities, Γ

is the boundary adsorption, Γ



is the triple junction (triple line)

adsorption.)

The fundamental thermodynamic characteristic of a triple junction is the

tension line γ



. The work required for a reversible increase of the triple junc-

tion length  by δ is

δW



= γ



δ (4.4)

As mentioned above, it is more reasonable to consider the joint change of the

length of the triple junction line and the area of the boundaries

δW

s



γ + γ



∂

∂



A (4.5)

For a constant temperature T ,volumeV , and the invariant chemical potentials

of the components (i=1,2,...k)

δW

s

= dΩ

T,V,μ

(4.6)

where Ω is the Gibbs grand potential.

For a system with a boundary and a triple junction

dΩ=−pdV −SdT −



dμ



γ + γ



∂

∂



A (4.7)

or (see Eqs. (1.5) and (1.6))

Ω=−pV + γ

A + γ



 (4.8)

For the surface-junction parameters Eq. (1.17) reads

dΩ

s

= −pdV

s

− S

s

dT −



s

dμ



γ + γ



∂

∂



A (4.9)

Then, from Eqs. (1.41) and (4.9)



dγ + dγ



∂

∂



= −S

s

dT −



s

dμ

+ V

s

dp (4.10)

Introducing the speciﬁc values s

s

s

, Γ

s

s

, v

s

s



dγ + dγ



∂

∂



= −s

s

dT −



s

dμ

+ v

s

dp (4.11)

Eq. (4.11) is the triple junction variant of the well-known Gibbs equation

4.2 Thermodynamics of Triple Junctions 333

which in this instance connects the change of boundary and triple junction

surface tension with a variation in temperature, pressure and chemical poten-

tials. For example, for a binary system at constant temperature and pressure,

using the Gibbs-Duhem relation (1.55) we arrive at



dγ + dγ



∂

∂



= −Γ

s

dμ

− Γ

s

dμ

= −



s

−

1 − c

s



dμ

(4.12)

where c is the concentration. In the framework of this approach, we cannot

achieve more. There is no dividing surface, either between the grain bound-

ary and the bulk (see Chapter 1), or between the boundaries and the triple

junction, and it is not possible to make one adsorption Γ

s

equal to zero by

changing the position of the dividing surface.

Let us consider a binary system with the concentrations c

and c

under

the assumption that the triple junction is in thermodynamic equilibrium with

its constituent boundaries and with the bulk. Then







,T,c





= μ



γ,T,c



= μ

(p, T, c

)







,T,c





= μ



γ,T,c



= μ

(p, T, c

) (4.13)

where μ



, μ



, μ

are the chemical potentials of the ﬁrst and

second component in the triple junction, at the grain boundaries, and in the

bulk, respectively, c



, c



, c

denote the respective triple junction and grain

boundary concentrations. The line tension stretches (or compresses, depending

on whether the line γ



is positive or negative) the triple junction, and the

equilibrium conditions can be written as

(p, T, c

)=μ





T,c





− γ





; (4.14)

(p, T, c

)=μ





T,c





− γ





isthelengthofanatomofthei-th component in the triple junction line.

Ifitcanbeassumedthat



,then

(p, T, c

) − μ





T,c





= μ

(p, T, c

) − μ





T,c





(4.15)

Taking both the bulk and triple junction as ideal solutions

= μ

+ kT ln c

(4.16)



= μ



+ kT ln c



The diﬀerence μ

− μ



= −γ





, inasmuch as the value γ





is the excess

energy of an atom of the ﬁrst component in the triple junction in compari-

son with the same atom in the bulk; γ



and γ



are the line tensions of the

triple junction in pure ﬁrst and second component, respectively. Combining

Eqs. (4.15) and (4.16)



1 − c

+ c



(4.17)

334 4 Thermodynamics and Kinetics of Connected Grain Boundaries

where B



=exp





−γ







. More complicated isotherms of triple junction ad-

sorption can be derived in analogy to the interface adsorption [197].

It is of interest to ﬁnd a relation between interface (in particular, grain

boundary) concentration and adsorption on a triple junction. Let us consider

the equilibrium between the grain boundary and triple junction constitution,

taking into account that the boundary is stretched by the surface tension γ

and the triple junction is stretched (or compressed) by the line tension γ



Then from Eqs. (4.14) and (4.15)

(T,c

) − γ

= μ





T,c





− γ





(T,c

) − γ

= μ





T,c





− γ





(4.18)

where A

is the area of an atom of the i-th component in the grain boundary.

Considering both the grain boundary and triple junction chemistry as ideal

solutions

= μ

+ kT ln c

(4.19)



= μ



+ kT ln c



By subtraction we obtain μ

− μ



= −







− γ



and μ

− μ



−







− γ



. These values represent the diﬀerence of the excess energy of

an atom of the ﬁrst and second component, respectively, in the triple junction

andintheinterface;γ

and γ

are the grain boundary surface tensions in the

respective pure components. For the simplest situation, when



,

A combining (4.18) and (4.19), we arrive at



s

1 − c

+ c

s

(4.20)

where

s

=exp







− γ





 − (γ

− γ

)



One can see from Eqs. (4.17) and (4.20) that the concentration in the triple

junction is rigidly bound not only to the concentration in the bulk of the

sample, but to the concentration in the interface, in particular, in the grain

boundary. It is felt that the detachment of adsorbed atoms from the grain

boundary should initiate the same phenomenon in the triple junction. In this

case the triple junction will no longer be in equilibrium with the bulk, but,

nevertheless, and what is of importance, is that it might still be in equilibrium

with the boundaries.

As already mentioned by Gibbs [1], although the line tension of a triple

junction might be negative, still the line of the triple junction (termed “ﬁla-

ment” by Gibbs) should be stable, and the phase of the triple junction would

diﬀer from the phase in the interfaces. “We may here add that the linear