Gottstein G., Shvindlerman L.S. Grain Boundary Migration in Metals: Thermodynamics, Kinetics, Applications
Подождите немного. Документ загружается.


294 3 Grain Boundary Motion
3.7 Compensation Effect in Grain Boundary Motion
3.7.1 The Fundamental Rate Equation
It is textbook knowledge that the temperature dependence of the absolute
rate ρ of thermally activated processes is governed by the Arrhenius relation
ρ = ρ
0
exp
−
H
kT
(3.188)
where ρ
0
denotes the preexponential factor, H the enthalpy of activation and k
is the Boltzmann constant. For evaluation of experimental data the activation
enthalpy is commonly determined from the slope −H/k of an Arrhenius plot
ln ρ vs. 1/T . Little attention is usually paid to the preexponential factor ρ
0
,
although it has been long known that ρ
0
changes, if the system is biased
such as to vary H. However, as we will show below, there is overwhelming
experimental evidence that the preexponential factor is strongly related to
the activation enthalpy: ρ
0
increases or decreases if H increases or decreases
according to the relation
H = α ln ρ
0
+ β (3.189)
Here α and β are constants, the meaning of which will be dealt with below.
Eq. (3.189) is referred to as compensation effect (CE), since it strongly moder-
ates the effect of a variation of H on the value of the absolute reaction rate ρ,
such that above a so-called compensation temperature, T
c
= α/k, the process
with the highest activation enthalpy has the highest reaction rate, while for
T<T
c
the process with the lowest value of H proceeds fastest.
Although the CE has been also reported for bulk processes, e.g. bulk diffu-
sion of solute atoms in a crystalline matrix [336, 337] or diffusion in whiskers
of different size [338], it is most pronounced in surface and interfacial reac-
tion phenomena, since in such cases the changes of H and ρ
0
can be quite
substantial. This was found for diffusion along grain boundaries and inter-
faces [339, 359, 367], grain boundary migration [274, 303] and spreading of
extrinsic grain boundary dislocations [368].
The CE probably was first reported by Constable [369] for dehydrogenation
of ethanol on a copper catalyst. More recently it has been found in other ther-
mally activated chemical, physical and biological processes and systems [370]–
[372]. The compensation effect in surface reactions and catalysis has been
associated with the interaction of adatoms in adsorbed surface layers [373]–
[377]. The variation of enthalpy and preexponential factor was attributed to
the number of ways in which the heat bath can furnish the energy needed
to overcome the barrier [378]. This, however, is closely connected with the
interactions in the adsorbed layers.
In this section we will review much of the existing data on the compensation
effect in thermally activated interface processes, although the fundamental
© 2010 by Taylor and Francis Group, LLC

3.7 Compensation Effect in Grain Boundary Motion 295
concepts hold for surfaces and bulk processes as well. Since it is difficult to
track details of data published by other authors, we shall restrict ourselves to
the considerable body of data obtained in our own interface research activi-
ties.
We will show that the compensation effect can be rationalized from ther-
modynamic fundamentals and how it applies to select solid state kinetics, in
particular grain boundary migration.
3.7.2 Examples
The CE manifests itself by a linear relation between the preexponential factor
ρ
0
and the activation enthalpy H, as expressed by Eq. (3.189). This equation
implies the existence of a temperature T
c
= α/k, the compensation temper-
ature (CT), where all reaction rates ρ of the considered group of thermally
activated processes are the same, i.e. the lines for the corresponding Arrhe-
nius plots intersect at temperature T
c
. Inserting Eq. (3.189) into Eq. (3.188)
at T = T
c
yields
ρ (T
c
)=exp
−
β
kT
c
(3.190)
In effect, the “Arrhenius coordinates” T
c
and β govern the kinetics of the
thermally activated process, since they uniquely link H and lnρ
0
according to
Eq. (3.189). In the following we present some pertinent examples for different
grain boundary processes.
The compensation lines H(lnA
0
) for the reduced mobility A = A
0
exp
(−H/kT) of 111 [274] and 100 [379] tilt boundaries in Al, 11
¯
20 tilt
boundaries in Zn [380] and 001 tilt boundaries in Sn [302] are given in
Figs. 3.113–3.116. The corresponding compensation temperatures are for Al
111: 450
◦
C, Al 100: 770
◦
C, Zn 11
¯
20: 420
◦
C, and Sn 001: 236
◦
C.
Fig. 3.117 shows results for Zn diffusion along tilt and twist boundaries in
Al [381]. In this case T
c
is in the range 450–500
◦
C. The CE is not confined
to single phase systems as is obvious from Figs. 3.118-3.120 [359, 382]. For
interface diffusion in 001 twist boundaries between Sn and Ge monocrys-
tals in two temperature ranges, namely 40
◦
C and 184
◦
C, the compensation
temperature equals 27
◦
C in the former and 220
◦
C in the latter temperature
regime. It is noted in this context that the gray-white phase transition in tin
takes place at a temperature of 20
◦
C.
3.7.3 Thermodynamics of the Activated State
3.7.3.1 Nature of the Activated State
The preexponential factor in the Arrhenius relation (Eq. (3.188)) consists of
some geometrical constants ρ
1
, a frequency factor ν andanentropyterm
exp(S/k), which depend on the kinetic quantity under consideration, like dif-
© 2010 by Taylor and Francis Group, LLC
296 3 Grain Boundary Motion
3
1
2
0
10
-5
10
-3
10
-1
10
3
10
1
10
5
10
9
10
7
A
0
[m
2
/s]
H
m
[eV]
3
1
2
0
10
-5
10
-3
10
-1
10
3
10
1
10
5
10
9
10
7
A
0
[m
2
/s]
H
m
[eV]
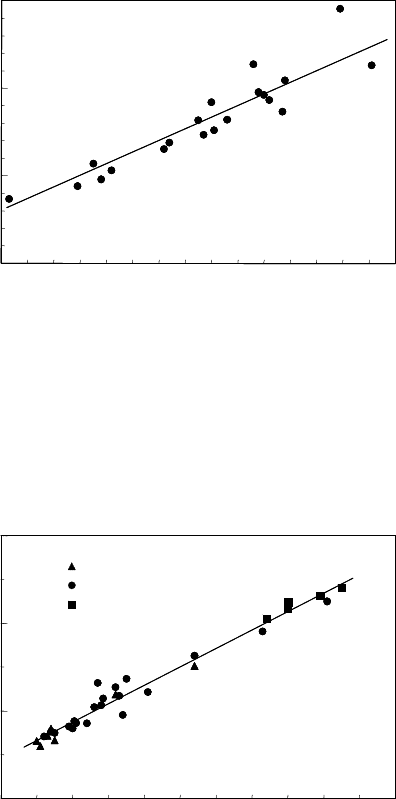
FIGURE 3.113
Dependence of migration activation enthalpy H
m
on the (reduced) pre-
exponential mobility factor A
0
for 111 tilt grain boundaries in Al.
H
m
[eV]
0
10
0
10
-6
10
-2
10
4
10
2
10
-4
A
0
[m
2
/s]
1
2
3
1
2
3
H
m
[eV]
0
10
0
10
-6
10
-2
10
4
10
2
10
-4
A
0
[m
2
/s]
0
10
0
10
-6
10
-2
10
4
10
2
10
-4
A
0
[m
2
/s]
1
2
3
1
2
3
FIGURE 3.114
Dependence of migration activation enthalpy H
m
on the (reduced) preex-
ponential mobility A
0
factor for 100 tilt grain boundaries in Al; 1 — Al
99.99995at.%; 2 — Al 99.9992at.%; 3 — Al 99.98at.%.
© 2010 by Taylor and Francis Group, LLC
3.7 Compensation Effect in Grain Boundary Motion 297
H
m
[eV]
10
-5
0.0
1.2
1.6
0.4
0.8
10
-7
10
-9
10
-1
10
-3
10
1
10
3
A
0
[m
2
/s]
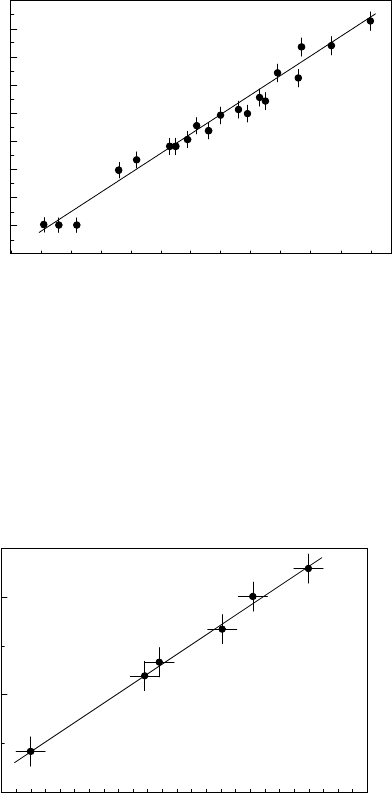
FIGURE 3.115
Dependence of migration activation enthalpy H
m
on the (reduced) preexpo-
nential mobility factor A
0
for 11
¯
20 tilt grain boundaries in Zn.
H
m
[
e
V
]
1
2
3
10
5
A
0
[m
2
/s]
10
10
10
15
10
20
10
25
10
30
FIGURE 3.116
Dependence of migration activation enthalpy H
m
on the (reduced) preexpo-
nential mobility factor A
0
for 001 tilt grain boundaries in Sn.
© 2010 by Taylor and Francis Group, LLC
298 3 Grain Boundary Motion
Twist GB
Tilt GB
Al / Zn
(s
δ
D
b
)
0
[m
3
/s]
Al / Zn
Twist GB
Tilt GB
10
-9
10
-11
10
-13
10
-15
10
-17
0.0 0.5 1.0 1.5
H
Db
[eV]
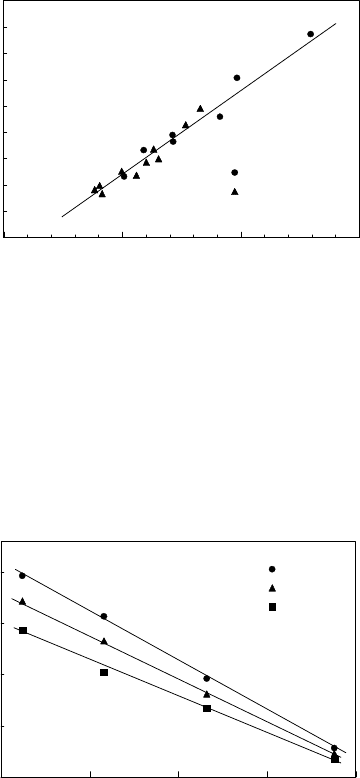
FIGURE 3.117
Dependence of the preexponential factor (sδD
b
) on activation enthalpy H
Db
for grain boundary diffusion of Zn along tilt and twist grain boundaries in Al.
1
2
3
D’
δ
[m
3
/s]
1
2
10
-18
3
10
-19
10
-20
10
-21
10
-22
2.25
2.50 2.75 3.00 3.25
1000/T [1/K]
FIGURE 3.118
Temperature dependence of the diffusional permeability of In in 001 twist
interphase boundaries in Sn-Ge. Misorientation angles: 1–2
◦
; 2–6
◦
; 0–3
◦
.
© 2010 by Taylor and Francis Group, LLC

3.7 Compensation Effect in Grain Boundary Motion 299
H
Db
[eV]
0.6
0.9
0.7
0.8
0.4
0.5
0.3
10
-17
D
b0
δ
[m
3
/s]
10
-13
10
-15
10
-11
10
-9
10
-7
FIGURE 3.119
Dependence of the activation enthalpy H
Db
for In diffusion along 001 twist
interphase boundaries in Sn-Ge on the preexponential factor D
b0
δ in the tem-
perature range 313–433K.
H
Db
[eV]
1.5
2.5
3.0
2.0
1.0
10
-5
10
0
10
5
10
10
D
bo
δ
[m
3
/s]
FIGURE 3.120
Same as Fig. 3.119, but in the temperature range 457–490K.
© 2010 by Taylor and Francis Group, LLC

300 3 Grain Boundary Motion
fusivity, mobility, chemical reaction rate etc. For a given material and ki-
netic process, ρ
1
ν is constant and for convenience the dimensionless quantity
ρ/ (ρ
1
ν)
∼
=
˜ρ canbeconsideredinstead,i.e.
˜ρ =exp
−
G
kT
=exp
S
k
exp
−
H
kT
=˜ρ
0
exp
−
H
kT
(3.191)
A linear relationship between H and log ˜ρ
0
is equivalent to the fact that the
entropy of activation is linearly related or even proportional to the activation
enthalpy. This observed coupling of entropy and enthalpy of activation sug-
gests that the activated state is not a random energy fluctuation in space and
time, but a defined and thus reproducible although unstable state, which is
described by its respective thermodynamic functions. Its attainment from the
stable ground state corresponds to a first-order phase transformation. In an
interface we can associate the activated state with a local change of the inter-
face structure, or more precisely, of a structure that the interface could attain
if a more stable state would not exist for the given thermodynamic conditions.
In this sense we consider the saddle point configuration of the activated state
as the minimum free energy configuration of all potential metastable states
for the given thermodynamic system (Fig. 3.121) and the attainment of the
activated state as a displacive phase transformation of first order. In this con-
cept the compensation temperature is the equilibrium temperature for such a
virtual phase transformation.
The compensation relation (Eq. (3.189)) can be easily derived under these
conditions. As an example we consider the grain boundary mobility m,which
is known to depend on grain boundary structure and chemistry. Application
of the Arrhenius relation (Eq. (3.191)) to the grain boundary mobility m
b
yields
ln m
b
=lnm
0
−
H
kT
=
S
k
−
H
kT
(3.192)
where S = klnm
0
and H represent the activation entropy and enthalpy of
grain boundary mobility, respectively.
Let the parameter λ denote some intensive structural or chemical specifica-
tion, like angle of misorientation, composition, surface tension etc. If λ changes
slightly from the reference state λ
0
,thenS and H change accordingly
ln m
0
(λ)=
S(λ)
k
=
1
k
S (λ
0
)+
dS
dλ
-
-
-
-
λ=λ
0
· (λ − λ
0
)+...
(3.193)
H(λ)=H (λ
0
)+
dH
dλ
-
-
-
-
λ=λ
0
· (λ − λ
0
)+... (3.194)
As S and H change only slightly, since G = H −T ·S is at minimum, a linear
approximation is sufficient, and solving Eq. (3.193) for λ − λ
0
yields
ln m
0
(λ)=
S (λ
0
) − H (λ
0
) /T
c
k
+
H(λ)
kT
c
(3.195a)
© 2010 by Taylor and Francis Group, LLC
3.7 Compensation Effect in Grain Boundary Motion 301
Γ
G*
Γ
’
G
G
o
G
*
Γ
Δ
x
′Γ
′
G
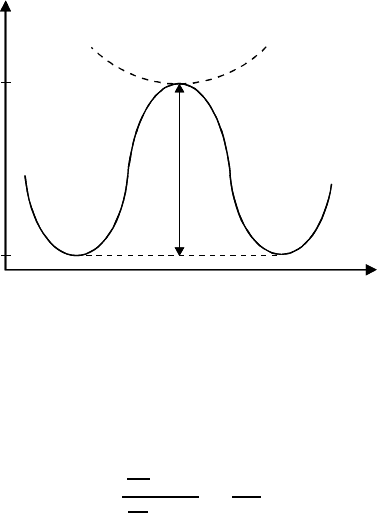
FIGURE 3.121
Simplified correspondence of thermally activated state Γ and thermodynami-
cally metastable state Γ
.
where
T
c
=
dH
dλ
-
-
λ=λ
0
dS
dλ
-
-
λ=λ
0
=
dH
dS
-
-
-
-
λ=λ
0
(3.195b)
is the compensation temperature, i.e. the equilibrium temperature between
ground state and activated state, or equilibrium phase and “barrier” phase.
This result implies that the barrier phase, i.e. the activated state, is a
metastable phase closely related to the equilibrium state. It corresponds to
a configuration of atoms with the smallest increase of potential energy with
respect to the ground state. It seems obvious that equilibrium states occur-
ring in the vicinity of the compensation temperature most easily satisfy this
requirement. These conclusions are supported by the observation that the
compensation temperature is often close to the equilibrium temperature of a
nearby phase transition [382]. Of course, when considering interface phenom-
ena, potential metastable phases need not be confined to bulk phases.
3.7.3.2 Equilibrium Thermodynamics Approach
The simplified treatment given above already delivers the CE, i.e. Eq. (3.189)
and defines the compensation temperature. In the following we shall give a
more complete treatment of the thermodynamics of the activated state, based
on the previously rationalized assumption that the transition from the equi-
librium state to the activated state is a first-order phase transition.
Let G
0
= H
0
− TS
0
denote the Gibbs free energy (referred to as free
energy in the following) of the equilibrium phase and G
= G
0
+ G
∗
≡
(H
0
+ H
∗
) − T (S
0
+ S
∗
) the respective function of the barrier phase. We
want to investigate the behavior of the barrier phase close to the point of
© 2010 by Taylor and Francis Group, LLC

302 3 Grain Boundary Motion
phase transformation. Enthalpy and entropy of the barrier phase are assumed
to depend on temperature, pressure and a constitutional parameter λ,asre-
ferred to in the previous section, which varies with modification of the inter-
facial system but does not noticeably affect the transformation temperature.
At a temperature T and pressure p near the transition point (T
c
,p
c
)
ΔG
=(G
− G
0
)=G
∗
∼
=
(ΔG
)
T
c
,p
c
+ (3.196a)
+
∂
∂T
(ΔG
)
T
c
,p
c
ΔT +
∂
∂p
(ΔG
)
T
c
,p
c
Δp + ...
where
ΔT = T − T
c
, Δp = p − p
c
(3.196b)
Introducing the thermodynamic functions
ΔG
= G
∗
= E
∗
−TS
∗
+pV
∗
∼
=
−S
∗
(T
c
,p
c
,λ)ΔT +V
∗
(T
c
,p
c
,λ)Δp (3.197)
we obtain
E
∗
= S
∗
(T
c
,p
c
,λ) T
c
+ T [S
∗
(T,p,λ) − S
∗
(T
c
,p
c
,λ)] − (3.198)
− V
∗
(T
c
,p
c
,λ) p
c
+ p [V
∗
(T
c
,p
c
,λ) − V
∗
(T,p,λ)]
Approximating the terms in the square brackets by a series expansion to first-
order
S
∗
(T,p
c
,λ) − S
∗
(T
c
,p,λ)
∼
=
C
∗
p
T
c
,p
c
,λ
T
c
ΔT +Δ
C
∗
p
T
ξ
T
c
,p
c
,λ
Δp + ...
because of c
p
/T =(dS/(dT ))
p,N
,whereN is the number of particles, and
introducing
ξ =
∂T
∂p
V,N
,η=
∂V
∂T
p,N
,ζ=
∂V
∂p
T,N
(3.199)
we arrive at
E
∗
∼
=
S
∗
(T
c
,p
c
,λ) T
c
+ T
C
∗
p
T
c
T
c
,p
c
,λ
ΔT + (3.200)
+ T
C
∗
p
T
ξ
T
c
,p
c
,λ
Δp − V
∗
(T
c
,p
c
,λ) p
c
+
+ p(η)
T
c
,p
c
,λ
ΔT + p(ζ)
T
c
,p
c
,λ
Δp
Then, if the intensive parameters of an experiment are not too different from
their value at compensation, i.e. ΔT/T
c
,Δp/p
c
1, Eq. (3.200) simplifies to
E
∗
∼
=
S
∗
(T
c
,p
c
,λ) T
c
− V
∗
(T
c
,p
c
,λ) p
c
(3.201)
© 2010 by Taylor and Francis Group, LLC

3.7 Compensation Effect in Grain Boundary Motion 303
Eq. (3.201) manifests a linear relation between the enthalpy and entropy (or
volume) of activation, i.e. there is a special, metastable, “barrier” phase, which
is attained by a first-order phase transformation at a critical temperature,
pressure, etc. and which we refer to as compensation temperature, pressure,
etc.
Thus, in analogy to the (temperature) compensation effect for constant
pressure at variable temperature, there is also a (pressure) compensation effect
for constant temperature at variable pressure. For a temperature T = T
c
close
to the transition temperature the free energy change owing to a change of
pressure from p
c
to p reads
ΔG
≡ G
∗
= E
∗
(λ) − TS
∗
(T,p
c
,λ)+pV
∗
(T,p
c
,λ)=V
∗
(T,p
c
,λ)Δp
(3.202)
Combining Eqs. (3.201) and (3.202)
TS
∗
(T,p
c
,λ) − T
c
S
∗
(T
c
,p
c
,λ)
∼
=
p
c
[V
∗
(T,p
c
,λ) − V
∗
(T
c
,p
c
,λ)] (3.203)
or in first-order approximation, introducing the coefficient of thermal expan-
sion α
∗
=1/V
∗
(dV
∗
/dT )
p,N
S
∗
(T,p
c
,λ)
∼
=
p
c
V
∗
α
∗
− c
∗
p
(3.204)
i.e. the entropy S
∗
is linearly related to the activation volume V
∗
.Infact,such
relation was experimentally verified (Fig. 3.122) [359]. In essence, the consid-
erations prove that the compensation effect can be derived from equilibrium
thermodynamics of the activated state which, in turn, can be associated with
a potential metastable state.
11
3.7.3.3 Irreversible Thermodynamics Approach
The activated state is not a stable equilibrium state and, therefore, the re-
turn of the system to the equilibrium state ought to comply with the laws of
irreversible thermodynamics. One of the fundamental principles of nonequi-
librium thermodynamics is the principle of maximum rate of change of the
thermodynamic potential of the system [260, 261, 383]. This means, as stated
by Ziegler [260], that a system with given thermodynamic forces strives for
equilibrium on the shortest way, i.e. at constant temperature and pressure
with the maximum rate of Gibbs free energy reduction. It is noted that this
pertains to relative rather than absolute minima of the thermodynamic po-
tential function, i.e. to the most stable intermediate state of the system.
In application of these principles to interface processes let us consider, as
11
It is noted that Eq. (3.196a) also holds if T is rather different from T
c
. Since the higher-
order terms d
n
S/dT
n
are practically zero, the series expansion of S(T ) can always be
truncated after the first-order term.
© 2010 by Taylor and Francis Group, LLC
