Gottstein G., Shvindlerman L.S. Grain Boundary Migration in Metals: Thermodynamics, Kinetics, Applications
Подождите немного. Документ загружается.


284 3 Grain Boundary Motion
correspondingly. is the thickness or width of the sample.
In this case the reduction in grain boundary mobility is equal to
Δm
m
≈
σv
c
2
(3.182)
The approach put forward in [340] permits us to analyze the different con-
figurations of a grain boundary in the magnetic field. For example, for the
configuration considered in Fig. 3.105a the relations for H
G
can be expressed
as
H
G
=
I
c
=
2σvd
m
ΔχH
c
2
(3.183)
The magnetic field H
G
(Eq.(3.183)) acts as a dragging force F which causes
a change in grain boundary mobility
Δm
m
≈
2σvd
m
Δχ
c
2
(3.184)
The magnetic thickness d
m
may be much larger than the “crystallographic”
grain boundary thickness, since it does not have to be smaller than the “for-
mation length” of the magnetic susceptibility.
Generally, the relative change in grain boundary mobility is reasonably de-
scribed by the order of magnitude given by Eq. (3.184). The comparatively
large magnetic field generated in the volume V ∼
3
(contrary to r
3
for the
microscopic approach, where r is in the range of the lattice constant) in the
course of grain boundary motion increases essentially the dragging force due
to the conversion of magnetic energy into Joule heat and in turn the change
of grain boundary mobility
F
Joule
=
σv
c
2
3
2
d
2
m
(ΔχH)
2
(3.185)
Δm
Joule
m
=
σv
c
2
3
d
m
2
Δχ
κ
(3.186)
where κ is the “configuration” coefficient of the magnetic driving force κ =
P
ΔχH
2
. One can see that the Joule dragging force F
Joule
is proportional to v
4
contrary to the Lenz dragging force F , which is associated exclusively with
the magnetic field induced by grain boundary motion F ∼ v
2
.
The numerical estimates do not render very high values of the magnetically
induced dragging force — in the range of 10
−3
:
Δm
m
≈ 10
−3
for the effect of
Joule dragging [340]. However, it is stressed that the very strong dependency
of the mobility reduction on the grain boundary velocity (Eq. (3.186)) can
tangibly affect the final result.
The approach put forward in [340] is one way to explain the strange results
of grain boundary mobility measured during the boundary motion in opposite
directions, as described in Sec. 3.5.9.3. The electromagnetic dragging force in
© 2010 by Taylor and Francis Group, LLC
3.6 Effect of Wetting Phase Transitions on Grain Boundary Migration 285
1.8 1.85 1.9 1.95 2 2.05 2.1
10
3
/T [K
-1
]
10
-8
10
-7
10
-6
m
[
m
4
/
J
s
]
1E-008
1E-007
1E-006
210
230250270
T [°C]
T
c
1.8 1.9 2.0 2.1
10
-8
10
-7
10
-6
270 250 230 210
T [°C]
1000/T [1/K]
m
b
[m
4
/Js]
1.8 1.85 1.9 1.95 2 2.05 2.1
10
3
/T [K
-1
]
10
-8
10
-7
10
-6
m
[
m
4
/
J
s
]
1E-008
1E-007
1E-006
210
230250270
T [°C]
T
c
1.8 1.9 2.0 2.1
10
-8
10
-7
10
-6
270 250 230 210
T [°C]
1000/T [1/K]
m
b
[m
4
/Js]
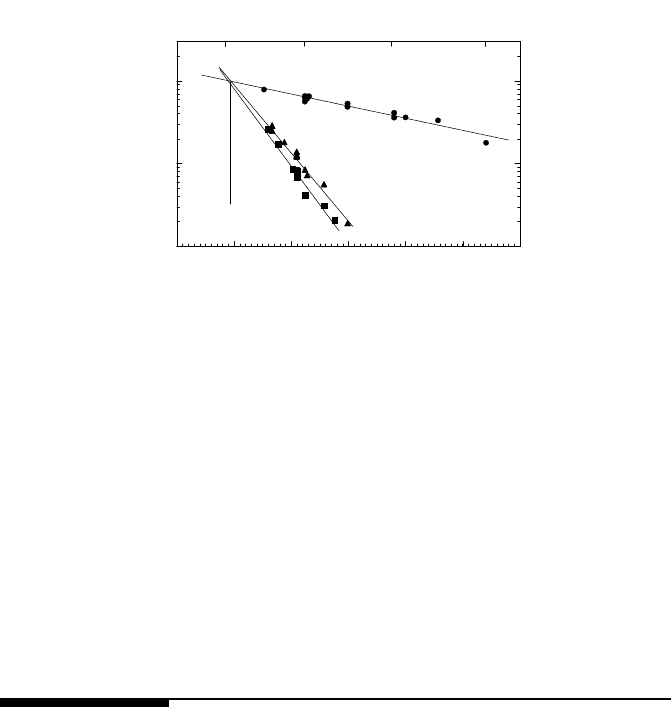
FIGURE 3.106
Temperature dependence of symmetrical and asymmetrical tilt boundaries in
Bi.
a strong magnetic field cannot quantitatively explain the observed results,
though. We would like to emphasize that the discussed effects are applicable
to the motion of any defect in solids, especially for the high speed movement
of dislocations in a magnetic field. In any event, if this asymmetry of grain
boundary mobility also holds for other metals, it would have a serious impact
on our understanding of grain boundary motion, since the mobility of a grain
boundary is commonly conceived not to depend on its direction of motion.
3.6 Effect of Wetting Phase Transitions on Grain
Boundary Migration
Grain boundaries are liable to undergo phase transitions under certain condi-
tions. The character of grain boundary structure may change from a strongly
ordered CSL type (special) to a disordered (non-special or random) type with
rising temperature as discussed in Chapter 2. This structural transition must,
of course, be reflected in a discontinuous mobility change at the transition
temperature as was indeed observed experimentally (Fig. 3.107) [329]. In the
presence of alloying elements the boundary may be loaded with impurities
or break free from its segregated solutes, which again corresponds to a grain
boundary phase transition and thus markedly affects grain boundary mobility
as discussed at length in Secs. 3.3, 3.5.3 and 3.5.5.
If the alloying elements can give rise to a chemical phase transformation
© 2010 by Taylor and Francis Group, LLC
286 3 Grain Boundary Motion
10
-8
10
-9
10
-10
10
-11
A
b
[m
2
/s]
T [°C]
2.052.05 2.10
215
2.10
205 210 200 215 205
1000/T
[1/K]
(a) (b)
(c)
2.10
10
-8
10
-9
10
-10
10
-11
A
b
[m
2
/s]
T [°C]
2.052.05 2.10
215
2.10
205 210 200 215 205
1000/T
[1/K]
(a) (b)
(c)
2.10
FIGURE 3.107
Temperature dependence of the reduced mobility of 001 tilt boundaries in
tin in the vicinity of a structural phase transition. Misorientation angles: (a)
28.2
◦
; (b) 29.0
◦
; (c) 29.5
◦
. Fig. 3.107b presents data for samples with different
migration driving force. The temperature T
c
of the structural transition is seen
to be independent of the migration driving force.
© 2010 by Taylor and Francis Group, LLC
3.6 Effect of Wetting Phase Transitions on Grain Boundary Migration 287
(dissociation) in the boundary, complex phenomena may arise due to the dif-
ferent properties of the bulk and boundary phase, e.g. in terms of composition
and melting. In this section we will consider grain boundary wetting phase
transitions in the systems Al-Ga and Al-Pb and their effect on grain boundary
mobility.
All known experiments on bicrystals have demonstrated a reduction in the
rate of grain boundary migration by impurities. Theoretically, this is ac-
counted for by the impurity drag theories, which predict a decrease in the
boundary mobility by adsorbed impurities. However, there are some remark-
able exceptions to the common rule that can cause unexpected and surprising
results. Examples of such unusual impurity effects on grain boundary mo-
tion were observed recently in aluminum doped with a minor amount of Ga
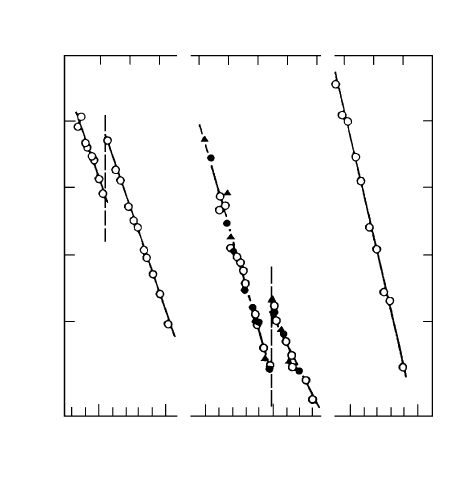
(10 ppm, Fig. 3.108) [330] or lead [331]. In contrast to other alloying elements
Ga (as well as Pb at high temperatures) raises the mobility and thus accel-
erates grain boundary migration in Al. This effect was studied on 111 tilt
grain boundaries with the angles of misorientation 38.2
◦
(Σ7) and 40.5
◦
.The
dramatic rise in grain boundary mobility with the addition of 10 ppm Ga was
interpreted in [330] as a consequence of a change in the boundary structure
and the mechanism of boundary migration owing to a pre-wetting phase tran-
sition and formation of a liquid (or quasi-liquid) Ga-rich layer on the grain
boundary.
In [332] this phenomenon was studied on the same 111 tilt grain bound-
aries (angles of misorientation are 38.2
◦
and 40.5
◦
), over a wide range of
Ga concentration. Fig. 3.108 demonstrates the temperature dependence of
boundary mobility for the boundaries investigated. The migration activation
enthalpy was found to be constant for a given grain misorientation over the
entire temperature range investigated for all Al alloys despite different Ga
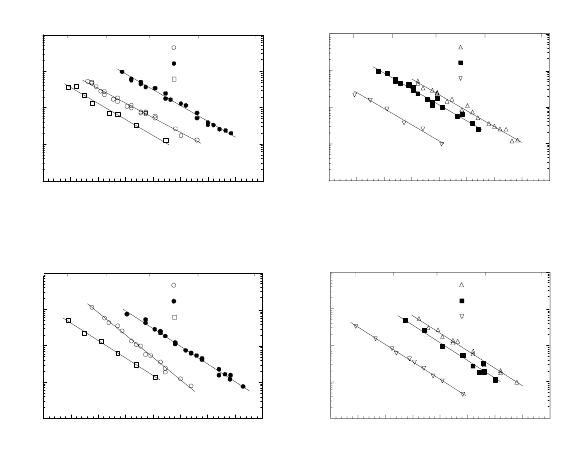
content. The concentration dependence of boundary mobility is presented in
Fig. 3.109. After the initial drastic rise, compared to pure Al, the boundary
mobility in Ga-doped aluminum decreases with increasing concentration of
Ga.
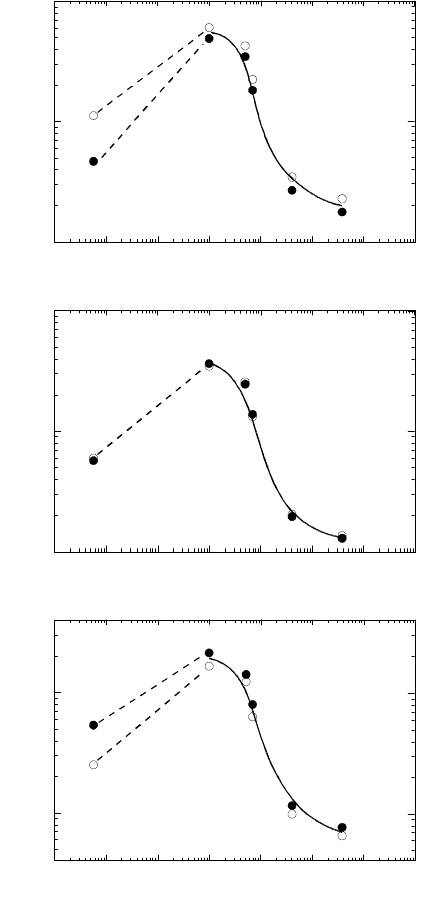
The behavior of a moving grain boundary in Al-Pb alloys differs substan-
tially from both the motion in pure Al and in Al-Ga alloys (Fig. 3.110). At a
certain temperature T
w
, which depends on the misorientation angle, the mi-
gration parameters (enthalpy of activation and pre-exponential factor) change
abruptly for both grain boundaries studied. Qualitatively, the same was ob-
served for 111 tilt boundaries with misorientation 38.2
◦
(special boundary
Σ7 and 40.5
◦
non-special boundary) [330]. The characteristic temperature T
w
is higher for the special boundary Σ7 than for the 40.5
◦
boundary. At rela-
tively low temperatures T<T
w
boundary motion is unstable (Fig. 3.110),
and the activation enthalpy of it in this temperature range is mostly smaller
than that for grain boundary migration in pure aluminum (Fig. 3.110). The
observed features of grain boundary motion in the Al-Pb alloy along with the
abrupt change in the boundary mobility and its parameters can be associated
with a grain boundary wetting phase transition [331]. The unstable boundary
© 2010 by Taylor and Francis Group, LLC
288 3 Grain Boundary Motion
1.2 1.3
1.4
1.5
1000/T [1/K]
1.2 1.3
1.4
1.5
1000/T [1/K]
1.1 1.2 1.3
1.4
1.5
1000/T [1/K]
1.2 1.3
1.4
1.5
1000/T [1/K]
A
b
[m
2
/s]
1.1
10
-10
10
-9
10
-6
10
-7
10
-8
1.1
10
-10
A
b
[m
2
/s]
10
-9
10
-6
10
-7
10
-8
600 550 500 450 400
T [°C]
600 550 500 450 400
T [°C]
600 550 500 450 400
T [°C]
600 550 500 450 400
T [°C]
Al + 70 ppm Ga
Al + 50 ppm Ga
Al + 0.38% Ga
Al (99.999%)
Al + 10 ppm Ga
Al + 410 ppm Ga
Al (99.999%)
Al +10 ppm Ga
Al +410 ppm Ga
Al + 50 ppm Ga
Al + 70 ppm Ga
Al + 0.38% Ga
1.1
10
-10
A
b
[m
2
/s]
10
-9
10
-6
10
-7
10
-8
(a)
10
-10
A
b
[m
2
/s]
10
-9
10
-6
10
-7
10
-8
(b)
1.2 1.3
1.4
1.5
1000/T [1/K]
1.2 1.3
1.4
1.5
1000/T [1/K]
1.1 1.2 1.3
1.4
1.5
1000/T [1/K]
1.2 1.3
1.4
1.5
1000/T [1/K]
A
b
[m
2
/s]
1.1
10
-10
10
-9
10
-6
10
-7
10
-8
1.1
10
-10
10
-9
10
-6
10
-7
10
-8
1.1
10
-10
A
b
[m
2
/s]
10
-9
10
-6
10
-7
10
-8
1.1
10
-10
A
b
[m
2
/s]
10
-9
10
-6
10
-7
10
-8
600 550 500 450 400
T [°C]
600 550 500 450 400
T [°C]
600 550 500 450 400
T [°C]
600 550 500 450 400
T [°C]
Al + 70 ppm Ga
Al + 50 ppm Ga
Al + 0.38% Ga
Al (99.999%)
Al + 10 ppm Ga
Al + 410 ppm Ga
Al (99.999%)
Al +10 ppm Ga
Al +410 ppm Ga
Al + 50 ppm Ga
Al + 70 ppm Ga
Al + 0.38% Ga
1.1
10
-10
A
b
[m
2
/s]
10
-9
10
-6
10
-7
10
-8
(a)
1.1
10
-10
A
b
[m
2
/s]
10
-9
10
-6
10
-7
10
-8
(a)
10
-10
A
b
[m
2
/s]
10
-9
10
-6
10
-7
10
-8
(b)
10
-10
A
b
[m
2
/s]
10
-9
10
-6
10
-7
10
-8
(b)
FIGURE 3.108
Temperature dependence of reduced boundary mobility for 111 tilt bound-
aries in Al with different contents of Ga (a) 38.2
◦
; (b) 40.5
◦
.
© 2010 by Taylor and Francis Group, LLC
3.6 Effect of Wetting Phase Transitions on Grain Boundary Migration 289
10
-8
10
-9
10
-10
10
-7
10
-8
10
-9
10
-7
10
-6
10
-8
10
-0
10
-2
10
-6
10
-4
c
Ga
[at.%]
10
-0
10
-2
10
-6
10
-4
c
Ga
[at.%]
10
-0
10
-2
10
-4
c
Ga
[at.%]
A
b
[m
2
/s]
A
b
[m
2
/s]
A
b
[m
2
/s]
(a)
(c)
(b)
10
-8
10
-9
10
-10
10
-7
10
-8
10
-9
10
-7
10
-6
10
-8
10
-0
10
-2
10
-6
10
-4
c
Ga
[at.%]
10
-0
10
-2
10
-6
10
-4
c
Ga
[at.%]
10
-0
10
-2
10
-4
c
Ga
[at.%]
A
b
[m
2
/s]
A
b
[m
2
/s]
A
b
[m
2
/s]
(a)
(c)
(b)
FIGURE 3.109
Dependence of reduced boundary mobility on Ga concentration for 38.2
◦
(◦)
and 40.5
◦
(•) 111 tilt boundaries in Al at different temperatures: (a) —
450
◦
C; (b) — 500
◦
C; (c) — 550
◦
C.
© 2010 by Taylor and Francis Group, LLC
290 3 Grain Boundary Motion
motion at somewhat lower temperatures is most probably related to the in-
teraction of the grain boundary with mobile liquid lead droplets. Above the
wetting transition temperature, the boundary is completely wetted by liquid
lead, and this drastically changes the mechanism of grain boundary motion.
Therefore, the observed temperature dependence of grain boundary migration
in Al doped with minor amounts (20 ppm) of Pb [331] suggests that the lead
solubility in Al is indeed negligible, so that even at concentrations as low as
20 ppm lead exists in aluminum as a second phase.
The size of lead particles can be estimated [331] using the experimentally
determined grain boundary mobilities at T<T
w
(Fig. 3.110). For fine parti-
cles their dominant mechanism of motion is the mechanism of surface diffusion
[207] (Table 3.2). The experimentally determined velocity of grain boundary
motion at T<T
w
can be considered as the critical velocity for the joint mo-
tion of grain boundary and particles. From this the radius of the particles was
estimated as 5 · 10
−8
≤ r ≤ 10
−7
m.
If grain boundary migration at T<T
w
is controlled by the mobility of
liquid lead droplets, then the activation enthalpy of grain boundary motion
should be close to the activation enthalpy of droplet motion [208]. This conclu-
sion is supported by the experimental data. As is well known, the activation
enthalpy for surface diffusion is significantly lower than that for the bulk dif-
fusion. The activation enthalpy for bulk self-diffusion in Al is H
D
∼ 1.5eV,
whereas the activation enthalpy for boundary migration at T<T
w
was found
to be 0.8–1.0 eV for both grain boundaries studied.
Wetting phenomena at grain boundaries require two phases (liquid and
solid) being in equilibrium with each other. The contact angle Θ depends on
the grain boundary surface tension γ and the surface tension of solid-liquid
interface γ
SL
: γ =2γ
SL
cosΘ (Fig. 3.111).
For γ ≥ 2γ
SL
the boundary is completely wetted by the liquid phase, and
Θ = 0. In the latter case the boundary cannot coexist with the liquid and is
replaced by a layer of the liquid phase. The temperature dependencies of the
surface tensions γ and γ
SL
are schematically shown in Fig. 3.112. The wetting
transition at the grain boundary occurs at the temperature T
w
,whereγ(T )
intersects 2γ
SL
(T ). If two grain boundaries have different surface tensions,
we may expect that their wetting transitions occur at different temperatures:
namely the lower the γ, the higher the T
w
. This agrees with experimental
results [331]: the energy of the Σ7 special boundary is lower than the energy
of the 40.5
◦
non-special boundary, and the wetting transition temperature for
the special grain boundary (T
w,s.
= 560
◦
C) is noticeably higher than that for
the non-special one (T
w,ns.
= 535
◦
C) (Fig. 3.110).
Usually the wetting transition at a grain boundary is observed under cir-
cumstances where a bicrystal is in contact (equilibrium) with a large amount
of liquid. Such type of wetting may be called an “external” wetting in contrast
to the “internal” wetting, when the wetting liquid is distributed as fine par-
ticles (droplets) in the bulk of the grains. For an internal wetting transition,
when the grain boundary becomes covered by a liquid layer of thickness λ at
© 2010 by Taylor and Francis Group, LLC
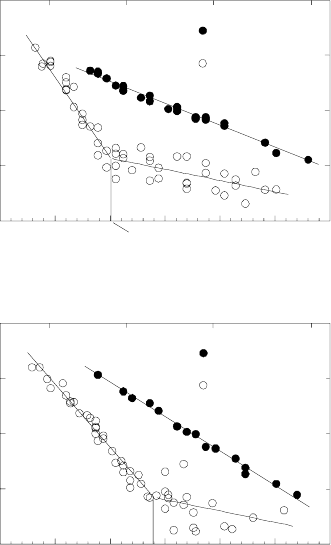
3.6 Effect of Wetting Phase Transitions on Grain Boundary Migration 291
1.1 1.2 1.3 1.4T
w
600
550 500 450
T [°C]
10
-6
10
-7
10
-8
10
-9
10
-10
A
b
[m
2
/s]
38.2°<111>
Al (99.999%)
Al + 20 ppm Pb
1.1 1.2 1.3 1.4T
w
600 550
500
450
10
-6
10
-7
10
-8
10
-9
10
-10
A
b
[m
2
/s]
40.5°<111>
Al (99.999%)
Al + 20 ppm Pb
T [°C]
1000/T [1/K]
1000/T [1/K]
FIGURE 3.110
Temperature dependence of reduced grain boundary mobility in pure Al and
Al-20 ppmPb.
© 2010 by Taylor and Francis Group, LLC
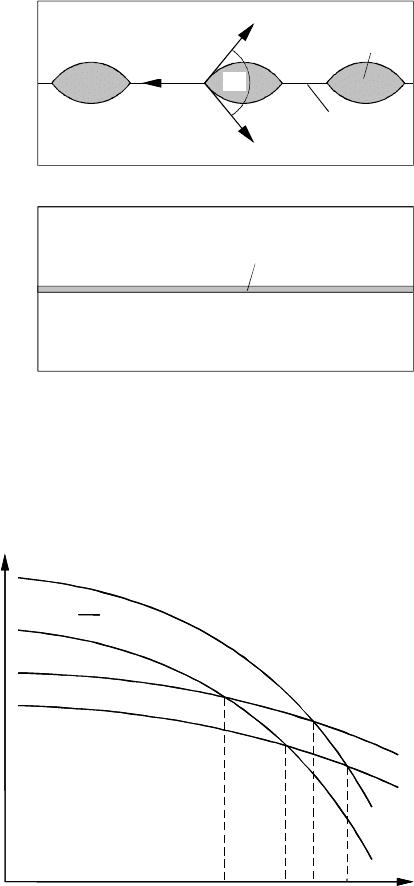
292 3 Grain Boundary Motion
crystal II
2θ
γ
GB
γ
SL
γ
SL
boundary
liquid
crystal I
crystal II
liquid
crystal I
(a)
(b)
crystal IIcrystal II
2θ
γ
GB
γ
SL
γ
SL
boundary
liquid
crystal I
crystal IIcrystal II
liquid
crystal Icrystal I
(a)
(b)
FIGURE 3.111
Illustration of the prewetting transition in a grain boundary. (a) Incomplete
wetting (2Θ > 0); (b) complete wetting (2Θ = 0).
γ
2γ
SL
2γ
SL
()1
3
2
−
λ
r
T
T
w
int
r
T
w
int
s
T
w
ext
s
T
w
ext
r
γ
r
γ
s
γ
2γ
SL
2γ
SL
()1
3
2
−
λ
r
2γ
SL
()1
3
2
−
λ
r
()1
3
2
−
λ
r
T
T
w
int
r
T
w
int
r
T
w
int
s
T
w
int
s
T
w
ext
s
T
w
ext
s
T
w
ext
r
T
w
ext
r
γ
r
γ
r
γ
s
γ
s
FIGURE 3.112
Schematic temperature dependence of surface tension at the solid/liquid in-
terface (2γ
SL
(T )), special boundary (γ
s
) and random grain boundaries (γ
r
).
© 2010 by Taylor and Francis Group, LLC

3.6 Effect of Wetting Phase Transitions on Grain Boundary Migration 293
the expense of droplets in the bulk, the change in free energy of the system
can be written as
ΔG = −γ +2γ
SL
−
3λ
r
γ
SL
(3.187)
The third term on the right-hand side of Eq.(3.187) describes the gain in free
energy due to the reduction of the total interphase (solid-liquid) area when
the liquid inclusions of radius r are transformed into a liquid boundary layer.
According to Eq. (3.187) and Fig. 3.112 the temperature of an internal wet-
ting transition should be lower than that of an external wetting transition,
which also corresponds to experimental observations [333].
In addition to the grain boundary wetting phase transition, where the
boundary is covered by a thin layer of a second phase, which is also a bulk
equilibrium phase under the given conditions, there is a prewetting (or pre-
melting) grain boundary transition when the grain boundary becomes covered
by a layer of definite thickness of a phase which is not an equilibrium bulk
phase under such conditions. The grain boundary phase transformation in
Al-Ga alloys is attributed to this kind of interfacial phase transitions. The ob-
tained results, i.e. decrease of boundary mobility and invariance of migration
activation enthalpy with increasing Ga concentration, are in agreement with
the hypothesis [330] that a change of boundary migration mechanism upon Ga
addition is associated with the formation of an interlayer of Ga-rich wetting
phase on the grain boundary. The rate controlling process of grain boundary
migration in this case cannot be the mass transport across the wetting phase
interlayer, because the activation enthalpy should then be on the order of 0.1
eV (activation enthalpy for diffusion in liquids), i.e. much smaller than ob-
served in experiment. Rather, grain boundary motion is apparently controlled
by the detachment of atoms from the shrinking grain, which occurs on the
crystal/interlayer interface. The magnitude of activation enthalpy is deter-
mined by the boundary migration mechanism, and must depend on structure
and properties of the crystal/interlayer interface, but obviously should be in-
dependent of the bulk impurity concentration. This was actually confirmed
by the experimental results (Fig. 3.108a).
A rise in the bulk Ga concentration leads to an increase in the bound-
ary thickness after the prewetting phase transition on the grain boundary, as
can be easily demonstrated in a quasi-chemical ideal solution approach of the
involved phases [334, 335].
© 2010 by Taylor and Francis Group, LLC
