Gottstein G., Shvindlerman L.S. Grain Boundary Migration in Metals: Thermodynamics, Kinetics, Applications

Подождите немного. Документ загружается.

264 3 Grain Boundary Motion

XI — Aleshin AN, Aristov VJ, Bokstein BS, Shvindlerman LS. Phys.

Stat. Sol. (a), 45:359, 1978.

XII — Beyeler M, Adda Y. J. P hys. (Paris), 345, 1978.

XIII — Makin SM, Rowe AH, Claire AD. P roc. P hys. Soc. Lond.,

70:545, 1957.

XIV — Gupta D. J. Appl. P hys., 44:4455, 1973.

XV — Wadja ES, Shirn GA, Huntington HB. Acta Metall., 3:39, 1955.

XVI — G¨unther F, Haessner A, Oppermann L. Isotopenpraxis, 5:461,

1969.

XVII — Buescher BJ, Gilder HM, Shea N. Phys. Rev., B7:2261, 1973.

XVIII — Okkerse B. Acta Metall., 2:551, 1954.

XIX — Nachtrieb NH, Resing HA, Rice SA. J. Chem. P hys.,

31:135, 1959.

XX — Hudson JB, Hoﬀman RE. Trans. Met. Soc. AIME,

221:71, 1961.

XXI — Lange W, Haessner A, Berthold I. P hys. Stat. Sol., 1:50, 1961.

XXII — Curtin HR, Decker DL, Vanﬂeet HB. Phys. Rev., A139:1551,

1965.

XXIII — Smithells CJ. Metals Reference Book, 5th ed, Butterworths,

London, 1976.

XXIV – Star, JP, Upthegrove WR. Trans. ASM, 59:479, 1966.

XXV — Hudson JB. in Aeronautical Research Laboratory T echnical

Report, Wright Air Development Center, Dayton,

OH, cited from Ref.XXIV, Report 60-321, 1966.

Moreover, Eq. (3.174) shows that high values of pressure are necessary to

obtain an impact on grain boundary motion by pressure comparable to the

measured temperature inﬂuence. To compensate for the eﬀect on grain bound-

ary mobility by a temperature change of the order of ∼250 K the pressure

should be changed by the order of ∼1 GPa. This demonstrates the serious

experimental problems which have to be overcome to properly measure the

pressure dependence of grain boundary mobility.

Grain boundary migration is the result of a net ﬂux of lattice sites across the

grain boundary. This means that the transfer of an atom across the boundary

causes a new lattice site to be produced on the grain boundary face of the

growing crystal, while a lattice site at the grain boundary face of the shrinking

crystal is removed. If the process of grain boundary migration occurs by both

the hopping of single atoms across the boundary for the diﬀusion migration

and activation volume, both close to an atomic volume is to be expected.

Owing to the substantial experimental diﬃculties, there are only few sources

in the literature that address this item. Hahn and Gleiter [305] studied grain

growth in pure Cd (99.9999%) under high pressure (up to 28 kbar (2.86 GPa))

and at annealing temperatures 180-260

◦

C. The activation volume was not

calculated by Hahn and Gleiter, but their data permit us to derive it [304].

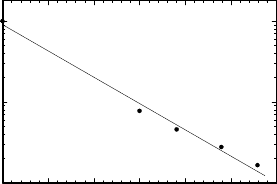
In Fig. 3.86 the rate of grain growth in Cd is given as a function of pres-

sure calculated in [124] from the data of [304]. It yields an activation volume

for grain growth, which can be associated with grain boundary migration:

3.5 Experimental Results 265

0 5 10 15 20 25 30

100

1000

100

1000

0 5 10 15 20 25 30

ln[(<D>

-<D

)/t]

p [10

MPa]

0 5 10 15 20 25 30

100

1000

100

1000

0 5 10 15 20 25 30

ln[(<D>

-<D

)/t]

p [10

MPa]

FIGURE 3.86

Pressure dependence of the mobility (∼ D

/t) during grain growth [304, 305].

∗

=6.39 cm

/mol, or V

∗

=0.49 · Ω

(Ω

— atomic volume). Since the

ratio V

∗

/Ω

for bulk self-diﬀusion in Cd ranges from 0.53 to 0.59, there is

reasonable agreement between V

∗

/Ω

and V

∗

/Ω

Lojkowski [306] studied grain growth in Al (99.99%) under a pressure up to

25 kbar (2.5 GPa) at 400

◦

C. The activation volume ranged from 0.65–0.8 Ω

and depended on the thermomechanical history, i.e. on crystallographic tex-

ture of the polycrystals. The values of the activation volume for self-diﬀusion

in Al given in the literature are contradictory and range from 0.52–1.35 Ω

(Table 3.7). The latter reference seems to provide more accurate data. In any

event, V

∗

≤ V

∗

As stressed many times, experiments on polycrystals provide only an aver-

age picture of the phenomenon. Also, as the majority of grain boundaries in

polycrystals have the character of random boundaries, the activation volume

of grain growth most likely reﬂects the activation volume of migration of ran-

dom grain boundaries.

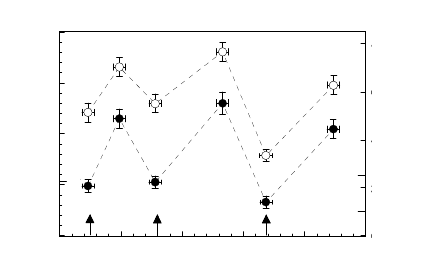
Special and non-special 001 tilt grain boundaries were studied in tin [302,

303, 307]. Grain boundary migration was measured at atmospheric pressure

and at high hydrostatic pressure up to 16 kbar. The orientation dependencies

of activation enthalpy and activation volume of migration are given in Fig.

3.87. The activation enthalpy for the migration of special grain boundaries

is 1.5–2 times larger than the energy of activation for bulk self-diﬀusion and

almost by an order of magnitude larger than for grain boundary self-diﬀusion,

whereas the activation volume for special grain boundaries amounts to 0.6–

0.96 V

∗

. However, for non-special grain boundaries the activation volumes

exceed V

∗

by a factor of 2–2.5. This is a ﬁrst indication that the activation

volume of grain boundary migration can substantially exceed the diﬀusion

activation volume.

The results of a comprehensive study of the temperature and pressure de-

266 3 Grain Boundary Motion

ϕ,

Σ Σ Σ

GBSD

20 25 30 35 40 45

Σ=13 Σ=17 Σ=5

V* [cm

/mol]

ϕ [deg]

[eV]

1.7

3.4

0.85

2.55

ϕ,

Σ Σ Σ

GBSD

20 25 30 35 40 45

Σ=13 Σ=17 Σ=5

V* [cm

/mol]

ϕ [deg]

[eV]

1.7

3.4

0.85

2.55

FIGURE 3.87

Activation enthalpy (◦) and activation volume (•)of001 tilt grain boundary

migration in tin.

pendencies of 100, 110,and111 tilt grain boundaries in bicrystals of pure

Al are given in Figs. 3.88 and 3.89 [304]. The activation volumes for 100 and

111 tilt boundaries are identical and independent of the angle of rotation,

quite in contrast to the behavior of the activation enthalpy. The absolute

value of about 12 cm

/mol corresponds to slightly more than one atomic vol-

ume in aluminum and is, therefore, close to the activation volume for bulk

self-diﬀusion. As mentioned above, the activation volume is the diﬀerence be-

tween the volume of the activated and the ground state. For self-diﬀusion this

is essentially the volume of a vacancy, which has to be provided for the ele-

mentary diﬀusive step. The ﬁnding of an activation volume for grain boundary

migration close to that of bulk self-diﬀusion suggests that a diﬀusion process

controls the boundary migration rate. On the other hand, the intrinsic grain

boundary mobility, e.g. in the absence of impurities, is not likely to yield ac-

tivation volumes very diﬀerent from a single atomic volume, since a diﬀusive

jump across the boundary by detaching an atom from the shrinking grain

and attaching it to the growing one requires the generation of a lattice site

at the internal surface of the growing crystal. If large structural vacancies do

not exist in the boundary, then the creation of a lattice site in the boundary

requires a volume change close to an atomic volume. In fact, computations of

grain boundary structure at 0 K do not predict large excess volumes in grain

boundaries, at least not in special boundaries. The results for 100 and 111

tilt boundaries are, therefore, quite in line with our current understanding of

grain boundary motion by the hopping of single atoms across the boundary.

By contrast the activation volume for 110 tilt boundaries increases with

increasing departure from the exact low Σ coincidence misorientation, as is

also the case for the activation energy (Fig. 3.88). For a 30

◦

110 bound-

3.5 Experimental Results 267

1.0 1.5 2.0 2.5 3.0 3.5

E [eV]

[

]

1 1.5 2 2.5 3 3.5

<100>

<111>

<110>

V* [cm

/mol]

1.0 1.5 2.0 2.5 3.0 3.5

[eV]

<100>

<111>

<110>

1.0 1.5 2.0 2.5 3.0 3.5

E [eV]

[

]

1 1.5 2 2.5 3 3.5

<100>

<111>

<110>

V* [cm

/mol]

1.0 1.5 2.0 2.5 3.0 3.5

[eV]

<100>

<111>

<110>

FIGURE 3.88

Activation volume vs. activation enthalpy of tilt grain boundary migration in

Al (tilt axis indicated).

ary, which deviates by ∼ 8

◦

from the Σ9 boundary, the activation volume

amounts to 36 cm

/mol equivalent to more than three atomic volumes. Such

large activation volume cannot be justiﬁed in terms of individual atomic jump

mechanisms of grain boundary migration. Rather, such values are evidence

that more than a single atom is involved in the fundamental process of grain

boundary migration.

Migration mechanisms, based on groups of atoms, can consist either of

the concomitant migration of groups or a cooperative motion (chain transfer)

by coordinated serial motion of atoms. Group mechanisms of grain boundary

migration have been proposed by several authors in the past, but without

any proof of evidence. In his island model of grain boundary structure, Mott

proposed that little patches of perfect crystal structure will detach from one

crystal and attach at the other side of the boundary [162]. Such a model of

grain boundary migration, however, is not compatible with our current knowl-

edge of grain boundary structure. Grain boundaries are very narrow with lit-

tle excess volume and do not give room for ﬂoating crystal patches across the

boundary. In a computer simulation carried out by Shan and Bristowe [308],

as well as Sch¨onfelder, Wolf et al. [309], it was found that concurrent shuﬄing

of groups of atoms may take place during migration.

3.5.9 Eﬀect of Grain Boundary Orientation

3.5.9.1 Anisotropy of Grain Boundary Motion

Thus far, we have considered the dependency of grain boundary mobility

on misorientation between the adjacent grains only. A grain boundary, how-

268 3 Grain Boundary Motion

-1

/s]

0.1 1 10 100 1000100001000001E+0061E+0071E+0081E+0091E+0101E+0111E+012

<100>

<111>

<110>

-1

/s]

V* [cm

/mol]

<100>

<111>

<110>

-1

/s]

0.1 1 10 100 1000100001000001E+0061E+0071E+0081E+0091E+0101E+0111E+012

<100>

<111>

<110>

-1

/s]

V* [cm

/mol]

<100>

<111>

<110>

FIGURE 3.89

Activation volume vs. preexponential reduced mobility factor of tilt grain

boundary migration in Al (tilt axis indicated).

ever, is also deﬁned by its spatial orientation (inclination), which is commonly

changing along the boundary between adjacent grains. It is usually tacitly as-

sumed that the (spatial) orientation of a boundary does not seriously aﬀect

grain boundary mobility. This is not always true, however, as evident from

recrystallized microstructures of fcc materials with low stacking fault energy,

which exhibit a high density of slim annealing twins (Fig. 3.90). Despite a

common orientation relationship the mobility of the long straight coherent

twin boundaries is obviously much lower than that of the other, incoherent

twin boundaries. Not only twin boundaries exhibit an anisotropy of mobility

for a given misorientation relationship. This is most easily demonstrated from

bicrystal experiments where a boundary is allowed to freely expand in a vol-

ume.

Such a case can be achieved by utilizing growth selection in a steep tem-

perature gradient of a slightly deformed single crystal with the shape of a

shovel [310] (Fig. 3.91). Growth selection is set oﬀ at the top of the handle

and is terminated when the remaining single grain boundary has reached the

bottom of the handle. Subsequently, the entire shovel is subjected to an an-

nealing treatment, during which the boundary freely expands into the blade

of the shovel, driven by the stored energy of cold work in the slightly rolled

single crystal shovel.

Although during growth selection certain orientations are strongly pre-

ferred over others in growth competition, other orientation relationships also

are occasionally observed to survive. From a large number of experiments it is

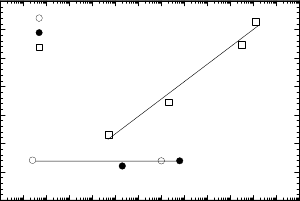
evident that grain boundaries with 100 and 110 rotation axis grow fairly

isotropically, i.e. the ﬁnal shape of the growing grain is a semicircle (Fig. 3.92).

For a 111 rotation axis a very anisotropic grain boundary mobility is ap-

parent, and the growing grain assumes the shape of a rectangle (Fig. 3.93).

3.5 Experimental Results 269

FIGURE 3.90

Microstructure of recrystallized brass. Note anisotropic grain shape of anneal-

ing twins.

FIGURE 3.91

(a) Principle of the production of a bicrystal from a deformed single crystal

in a gradient furnace; (b) idealized form of the used bicrystal.

270 3 Grain Boundary Motion

[001]

[010]

Grain α

Grain β

(a) (b)

[001]

[010]

Grain α

Grain β

(a) (b)

FIGURE 3.92

Isotropic grain growth of grain boundaries with 100 rotation axis. (a) Grain

β was nucleated spontaneously from the surface (b).

The long straight facet of the grown grain, i.e. the slowly moving boundary,

is determined by the crystallography of the growing grain rather than by the

shovel geometry. If the shovel is machined out diﬀerently from the rolled sin-

gle crystal, the spatial orientation of the slowly growing facet follows exactly

the change of the crystallographic directions in the deformed single crystal

(Fig. 3.94). The long facet is always perpendicular to the 111 rotation axis,

i.e. this slowly moving facet is a twist boundary. The degree of anisotropy Λ,

deﬁned by

Λ=

elongation

broadening

(3.175)

of the grain, is not a function of angle of rotation, but rather is strongly depen-

dent on the deviation of the actual rotation axis from an ideal 111 axis (Fig.

3.95). The more perfect the twist character of the boundary, the larger Λ, up

to a factor of 100 for the ideal 111 twist boundary, which is most perfectly

achieved for the coherent twin boundary. A deviation by 2 degrees reduces the

anisotropy already by a factor of 10. An ideal 111 twist boundary consists

of two perfectly ﬂat {111} planes of the adjacent crystals, and it is easy to

imagine that it is diﬃcult to remove or attach atoms to these planes, i.e. to

make the grain boundary move.

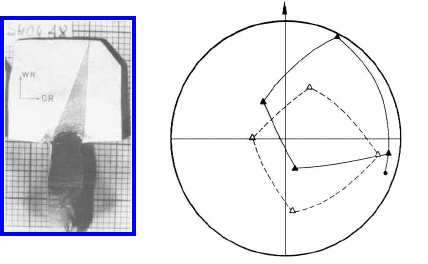
It was frequently observed that the growing grain assumed the shape

of a triangle rather than a rectangle (Fig. 3.96). One of the straight faces

was identiﬁed as a twist boundary, while the other triangular boundary was

faceted comprising piecewise twist boundary facets. For a single crystal ori-

entation symmetrical with regard to the growth direction in the handle of

the shovel, two symmetrically equivalent orientations frequently survived the

3.5 Experimental Results 271

FIGURE 3.93

Rectangular-shaped grain obtained by free planar growth in Al. Deformed

grain in Goss orientation (110)[001]. Orientation relationship between grains

approximately 46

◦

111.

growth competition, one of which became rectangular while the other one as-

sumed a triangular shape (Fig. 3.97). Although the reason for this behavior is

not yet clear, it may be related to the dependence of grain boundary mobility

on direction of motion, as will be shown in Sec. 3.5.9.2.

This anisotropy of grain boundary mobility manifests itself by an ellipticity

of grain morphology during free growth of a grain in a homogeneous environ-

ment. The ﬁrst-order twin boundaries (60

◦

111) are the most prominent, but

not the only example. For a general mathematical description of grain shape

evolution, the displacement of a grain boundary element parallel to its normal

has to be considered (Fig. 3.16). Including forces by grain boundary surface

tension γ and a volume driving force P for its motion, we arrive at the shape

evolution equation y(x, t) (see also Sec. 3.3.6)

∂y

∂t

= V − Pm

+ m

γκ (3.176)

where V is the speed of a (dragging) groove, and κ is curvature. If the bound-

ary slope is small ((∂y/(∂x)  1) then a linear equation is obtained

∂y

∂t

= V + m



∂

∂x

− P



(3.177)

The solution of this partial diﬀerential equation depends on the magnitude

of the driving forces and the orientation dependent mobility of the boundary.

272 3 Grain Boundary Motion

L D

R D

T D

C D

Al - rolled 30% Matrix: (011) [100] grain d:32° [D]

(a)

(b)

L D

R D

T D

C D

Al - rolled 30% Matrix: (011) [100] grain d:32° [D]

(a)

(b)

FIGURE 3.94

The same rolling sample as Fig. 3.93, (a) shovel cut in such a way that the

{111} plane is parallel to longitudinal direction (b).

[deg]

111

20 40 60 80

100

2460

100

(a)

(b)

[deg]

111

20 40 60 80

100

2460

100

(a)

(b)

FIGURE 3.95

Shape anisotropy A of grain grown with 111 rotation axis to consumed grain

in Al. (a) Dependence on rotation angle; (b) dependence on deviation of the

actual rotation axis from the ideal 111 axis.

3.5 Experimental Results 273

11°

T D

(a) (b)

11°

T D

(a) (b)

FIGURE 3.96

Triangular-shaped grain (a); the orientation of the triangular-shaped grain

(b).

For an isotropically moving boundary the solution will be a sphere in three

dimensions or a circle in two dimensions. For the general case, i.e. more com-

plicated conditions with regard to mobility and surface tension, solutions are

yet to be derived.

3.5.9.2 Impact of Boundary Orientation on the Steady-State

Motion of Curved Grain Boundaries

The growth selection experiments have shown the high anisotropy of 111

grain boundaries in the course of grain growth [310].

The steady-state motion of a grain boundary under the action of its own

surface tension was analyzed in Sec. 3.4.3. Since the diﬀerently inclined bound-

ary elements may have diﬀerent reduced mobilities, in general the velocity of

a curved boundary moving in steady state depends on its orientation [256].

The only exception are tilt grain boundaries in a crystal lattice with inversion

symmetry (100 tilt boundaries). Such eﬀect was observed, for instance, for

half-loop migration of 11

20 tilt boundaries in Zn [247].

In [311] an attempt was undertaken to consider this phenomenon for the

steady-state motion of 111 tilt and mixed tilt-twist grain boundaries in Al

bicrystals. The steady-state motion of a quarter-loop boundary in two con-

ﬁgurations was studied (Fig. 3.98). The boundary conﬁguration sketched in

Fig. 3.98a can be represented by a series of diﬀerently inclined “pure tilt” ele-

ments whereas the boundary with the conﬁguration of Fig. 3.98b is composed

of a series of mixed tilt-twist elements with changing twist component along

the boundary.

The motion of curved grain boundaries with rotation axis 111 and

misorientation angles between 34

◦

and 42

◦

in both conﬁgurations shown in