Gottstein G., Shvindlerman L.S. Grain Boundary Migration in Metals: Thermodynamics, Kinetics, Applications

Подождите немного. Документ загружается.

254 3 Grain Boundary Motion

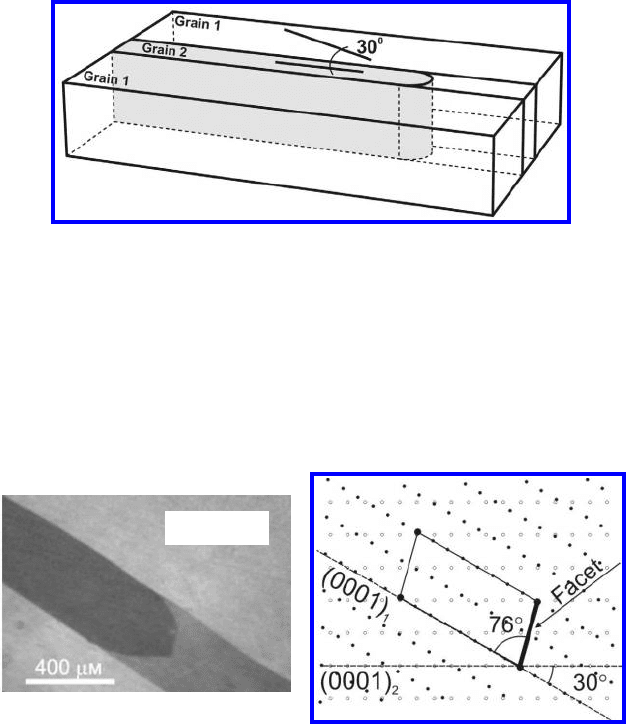
FIGURE 3.80

Scheme of a Zn bicrystal containing [10

10] tilt GBs with misorientation angles

of 30

◦

. The lines on the top faces of the crystals denote the orientation of basal

plane (0001) in each grain [320].

(a) (b)

T = 673 KT = 673 K

(a) (b)

T = 673 KT = 673 K

FIGURE 3.81

(a) Video frame of a moving grain boundary half-loop with facets [320]. (b)

Section of CCSL perpendicular to the [10

10] tilt axis for GBs with misori-

entation angle θ of 30

◦

. Filled and empty circles mark the sites of the two

misoriented Zn lattices. Large circles mark CCSL sites. The reciprocal den-

sity of coincidence sites is Σ = 17. The unit cell of the respective CCSL, the

position of the basal plane (0001) for grain 2 and the CCSL plane parallel to

the facet on the moving GB are also shown [320].

3.5 Experimental Results 255

620 640 660 680 700

0,0

0,1

0,2

0,3

0,4

0,5

Normalized facet length l

Temperature (K)

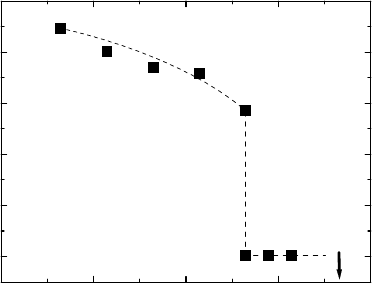
FIGURE 3.82

Observed temperature dependence of the facet length  [320].

steady-state motion of the individual grain boundary — [10

10] and [11

20] tilt

grain boundary half-loop (Figs. 3.80, 3.81) — and in situ recording of grain

boundary motion. Above a certain temperature (673K for [10

10] boundaries)

the migrating GB half-loop was continuously curved. Below this temperature

a facet appeared and coexisted with the curved GB. The length of the facet

increased with decreasing temperature (Fig. 3.82 [320]). The formation of a

grain boundary facet is usually due to a low grain boundary energy for the

speciﬁc facet inclination. From geometrical arguments, a low GB energy can

be associated with a high density of coincidence points of a coincidence site

lattice (CSL) [166, 316, 322]. The c/a ratio of the lattice spacing a in the basal

plane (0001) and c perpendicular to (0001) is irrational in Zn. Therefore, exact

coincidence site lattices exist in Zn only for GBs with [0001] rotation axis. In

all other cases, including [10

10] tilt GBs, a so-called constrained coincidence

site lattice (CCSL) exists [323]. A section of the CCSLs perpendicular to the

[10

10] tilt axis is shown in Fig. 3.81 for a GB with misorientation angle of 30

◦

Filled and open circles, respectively, mark the lattice points of the two mis-

oriented Zn lattices. Large gray circles mark the CCSL sites. Evidently, the

points of both lattices do not coincide exactly, and the diﬀerence may reach a

few percent of the lattice spacing. This situation is similar to near-coincidence

GBs of materials with cubic lattice, when the misorientation angle is close but

not equal to the misorientation of exact coincidence θ

, although still inside

the range for special GBs [320, 324]. The reciprocal density of coincidence

256 3 Grain Boundary Motion

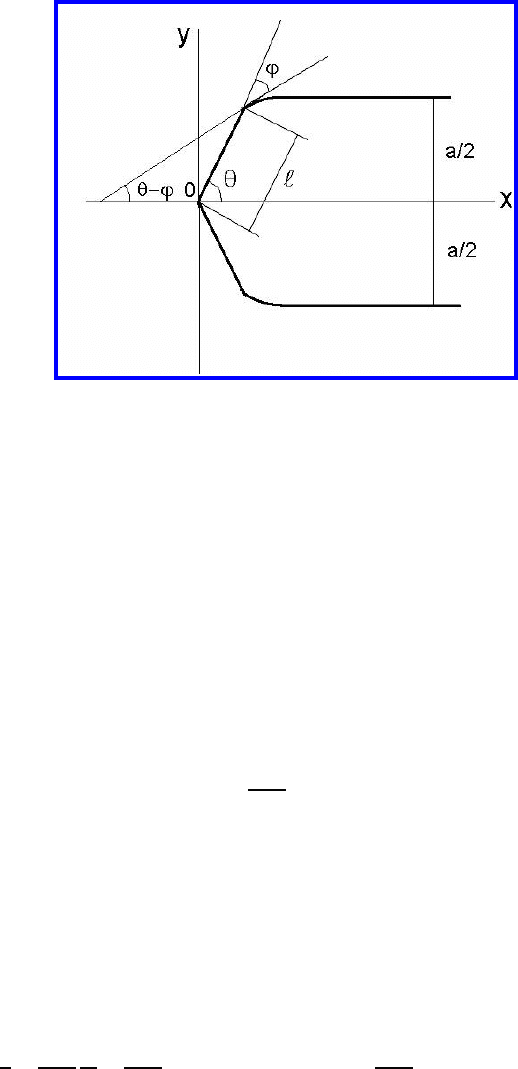
FIGURE 3.83

Geometry of a grain boundary half-loop with a facet [320].

sites for the studied 30

◦

[10

10] GB is Σ = 17, for the 85

◦

[11

20] grain boundary

Σ = 11.

Let us consider the steady-state motion of a grain boundary half-loop with

a facet. A schematic sketch of the considered faceted boundary is given

in Fig. 3.83 [320]. It resembles closely the experimentally observed shape

(Figs. 3.80, 3.81).

The equation of motion and the boundary conditions which deﬁne the

steady-state shape and the velocity V of a moving half-loop are given in [320].

In case of a partially faceted boundary the respective equations of motion and

the boundary conditions (a − c) for the curved boundary read (Fig. 3.83)



= −

γm





1+y

2



(a) y



( cos θ)=tan(θ − ϕ)

(b) y(∞)=a/2 (3.161)

Since the facet is ﬂat with inclination θ (Fig. 3.83) the shape of the curved

part of the moving half-loop with a facet is given by the equation

y =

−

arc cos



sin(θ − ϕ)exp



( cos θ − x)



(3.162)

3.5 Experimental Results 257

The velocity of the moving half-loop can be extracted from the boundary

condition (c) which renders

V =

γ(θ − ϕ)

−  sin θ

(3.163)

Since for steady-state motion the faceted and curved segments of the half-loop

have to move with the same velocity, the migration rate of the grain boundary

half-loop with a facet is also controlled by the facet motion. Formally the facet

velocity can be expressed as

V = m

κ (3.164)

where m

,γ

are the mobility and surface tension of the facet, γ

= γ cos ϕ

(see Fig. 3.83). The equivalent curvature of the facet κ can be found from the

so-called weighted mean curvature approach [73, 318]. The weighted mean

curvature is deﬁned by the reduction of the total interfacial free energy in

the course of an inﬁnitesimal facet displacement divided by the volume swept

by the displaced facet. Then the velocity of the facet can be expressed as

(Fig. 3.83))

V =

γ sin ϕ sin θ



(3.165)

From Eqs. (3.162) and (3.165) we obtain the length of a moving facet

 =

sin θ +

(θ−ϕ)

sin ϕ sin θ

(3.166)

Eq. (3.166) allows us to derive the mobility of the facet and its temperature

dependence from experimentally measured values of the facet length. For ex-

ample, the normalized facet mobility (m

) for the facet in a [10

10] grain

boundary system as extracted from experimental data is presented in Fig. 3.84

[320].

Apparently, a reduction of the facet length with rising temperature is mainly

caused by a decrease in the ratio m

. On the other hand, the absolute

value of the facet mobility can be extracted if the grain boundary mobility is

known from an independent experiment (Fig. 3.85) [320, 321]. As can be seen

the facet has a high mobility with a very low activation enthalpy (∼ 0.1eV).

An increase in the facet length with increasing facet mobility seems coun-

terintuitive, since it is a frequent observation that faceted boundaries move

with low mobility [310, 324]. The high mobility of the facet is associated with

a low activation energy and attributed to a high step mobility on the facet

[247, 320]. Such interpretation tacitly assumes that the production rate of

steps on the facet is suﬃciently high and will not aﬀect the facet velocity.

For instance, steps may be injected into the facet from the shrinking part of

the boundary. This may not be true, though, for smooth low energy facets

like coherent twin grain boundaries. In such case the migration rate may be

258 3 Grain Boundary Motion

640 645 650 655 660 665 670 675 680

Temperature, K

370 375 380 385 390 395 400 405 410 415

Temperature,K

(K)

370 375 380 385 390 395 400 405 410 415

Temperature,K

(K)

(a) (b)

640 645 650 655 660 665 670 675 680

Temperature, K

370 375 380 385 390 395 400 405 410 415

Temperature,K

(K)

370 375 380 385 390 395 400 405 410 415

Temperature,K

(K)

(a) (b)

FIGURE 3.84

(a) Temperature dependence of the ratio of the normalized facet mobility

for a [10

10] tilt grain boundary [320]. (b) Temperature dependence of

the ratio of the facet mobility and boundary mobility m

for a [11

20] tilt

grain boundary [321].

determined by the production rate of steps on the facet rather than by step

migration and consequently, a steady-state motion with a facet of ﬁnite length

may not be possible according to Eq. (3.166). Yoon [325] proposed that be-

sides the faceting transition there may also be a roughening transition where

smooth facets become rough owing to entropy-driven defect generation (steps,

vacancies).

It is noted that the dynamic facet length given by Eq. (3.166) is equiva-

lent to a maximum rate of free energy decrease [321]. As shown in Sec. 3.4.3

the velocity V of a half-loop as a whole corresponds to an extremum of the

function Ψ(V ) (3.146). Only maxima of this function correspond to stable

steady-state motion. For a linear dependence of the velocity on the driving

force (M (V ) = const.) the extremum of the function Ψ(V )isequivalentto

the maximum rate of reduction of free energy of the system (dissipation rate),

in other words, the system tries to reduce the free energy as fast as possible,

i.e. with the maximum possible rate.

For the steady-state motion of a grain boundary half-loop with a facet the

average mobility can be deﬁned in two ways, either by the facet motion or by

the motion of the curved boundary. In the ﬁrst case — the half-loop motion

is controlled by the facet motion — the average mobility can be expressed as

[321]

(V )=

2γ/a

a sin ϕ sin θ

2

(3.167)

3.5 Experimental Results 259

1,48 1,49 1,50 1,51 1,52 1,53 1,54 1,55 1,56

-8

-7

-6

, m

1000/T, K

-1

FIGURE 3.85

Temperature dependence of the facet mobility for a [10

10] tilt grain boundary

[321].

When the half-loop migration rate is determined by the motion of the curved

grain boundary the average mobility is

(V )=

(θ − ϕ)a



−  sin θ



(3.168)

A maximum rate of free energy reduction of the system is obtained for a

constant average mobility

(V )=M

(V ) (3.169)

Obviously condition (3.169) is satisﬁed by relation (3.166). In essence, the

facet changes its length in the course of motion in order to permit the system

to reduce its free energy with the highest rate, which in turn is related to the

Onsager principle of irreversible thermodynamics.

3.5.8 Eﬀect of Pressure on Grain Boundary Migration:

Activation Volume

As derived in Sec. 3.5.2, the grain boundary mobility is given by Eqs. (3.157)

and (3.158)

= m

exp



−



= E

+ pV

∗

260 3 Grain Boundary Motion

If an experiment is carried out at constant pressure the pre-exponential factor

and the enthalpy of activation H

can be derived from the temperature de-

pendency of grain boundary mobility. However, the enthalpy of activation and

the pre-exponential factor are not independent of each other (compensation

eﬀect, Sec. 3.7). Therefore, from mobility measurements at diﬀerent temper-

atures only information on a single activation quantity can be obtained.

The measured activation enthalpies for grain boundary motion are diﬃcult

to interpret. The problem of impurity inﬂuence on boundary mobility and,

in particular, on migration activation enthalpy was discussed above. It was

shown that despite a decrease in the activation enthalpy of boundary migra-

tion with rising impurity content, the activation enthalpy of migration for

most grain boundaries is signiﬁcantly greater than the activation enthalpy of

grain boundary diﬀusion and, in many instances, can even exceed the activa-

tion enthalpy of bulk diﬀusion (Figs. 3.51, 3.55, 3.56). Even if the interaction

between the adsorbed atoms is taken into account, at least in a very pure

material, there is a drastic diﬀerence between the rate theory of single atom

hopping and experimental results.

A more direct measure of the migration mechanism is the activation vol-

ume. The activation volume reﬂects the diﬀerence between the volume of the

system in the activated and in the ground state. The activation volume V

∗

can be obtained from measurements of the pressure dependence of Gibbs free

energy of activation

G = H −TS = E + pV

∗

− TS (3.170)

∂ ln v

∂p

= −

∗

(3.171)

∂ ln v

∂1/T

= −

(3.172)

For instance, the activation volume for bulk self-diﬀusion ought to be in the

order of one atomic volume. In this case the activated state consists of the va-

cancy production and the local lattice expansion caused by the diﬀusing atom

in the saddlepoint conﬁguration. The relaxed volume of a vacancy roughly

corresponds to a little less than an atomic volume, and the lattice expansion

during the diﬀusive jump will be small compared to an atomic volume. The

activation volume for grain boundary diﬀusion is only a little less than that for

bulk diﬀusion (Table 3.7). This can be easily understood, because the density

of grain boundaries is not very diﬀerent from the bulk density of the crystal

(even during melting the density of a metal drops only a few percent) (see

Chapter 1). With regard to grain boundary motion the value of the activation

volume is expected to provide information on essentials of the grain boundary

migration mechanism.

Despite the relative ease of interpretation of the activation volume com-

pared to the activation enthalpy, there have been only very few studies on

3.5 Experimental Results 261

the pressure dependence of grain boundary migration [302]–[304]. The main

reason for this deﬁciency is the serious experimental problems that have to be

overcome in order to successfully conduct experiments on grain boundary mi-

gration at high hydrostatic pressure. Beginning with the pressurizing medium,

either a gas or a liquid should be stable up to high temperatures and must be

inert to the material of the sample to avoid contamination of the specimen.

Moreover, the high pressure device must be designed to provide a stable and

homogeneous temperature ﬁeld. The displacement of a grain boundary during

annealing at high pressure is given by

 = vt = v

t exp



−



exp



−

∗



(3.173)

where v is the grain boundary velocity, t is the annealing time, v

is the pre-

exponential velocity factor. For a ﬂuctuation of temperature δT and pressure

δp and an inaccuracy of time measurement δt, the relative error of the grain

boundary displacement reads [304]

Δ





δT





∗

δp



δt

(3.174)

Obviously, the uncertainty of grain boundary displacement will be essentially

determined by the stability of pressure and temperature in addition to the

magnitude of the activation energy and activation volume. For E

∼

1.3eV,

∼

K, V

∗

∼

10 cm

/mol, at a pressure of the order of 100 MPa, a minor

ﬂuctuation of temperature by δT

∼

1 K is equivalent to a change of pressure

by 15 MPa. Therefore, a high stability of pressure and temperature is required

for an accurate measurement.

262 3 Grain Boundary Motion

TABLE 3.7

Parameters of Bulk Diﬀusion

Metal Specimen H

bulk

/s] V

∗

bulk

/Ω

[eV]

Ag self- polycrystals 2.0 8.9 · 10

−3

diﬀusion

[I]

Ag self- 001 tilt 1.97 7.2 · 10

−5

diﬀusion grain boundary

[II] ϕ =28

◦

Ag self- polycrystals 1.87 2.78 · 10

−5

diﬀusion

[III]

Ag self- single crystal 0.66 [IV ]

diﬀusion “pure” silver 0.88 [V ]

polycrystals 1.28 2.45 · 10

−5

1.1 [VII]

Al-Zn ϕ =32

◦

[VI][VI]

ϕ =37

◦

1.35 1.4 · 10

−4

111 tilt [X][X]

grain boundary

Al self- 1.23 − 1.35

diﬀusion [XII]

Al-Cu single crystal 1.16

Al-Ag “pure” Al single 1.19

Al-Au crystal of Al 1.18

[V ]

Au self- polycrystals 1.8 9.1 · 10

−6

0.67 − 0.81

diﬀusion [XIII][XII]

Cd self- polycrystals Q

=0.79 = 1.3·⊥C

diﬀusion 99.9995 at% Q

⊥

=0.82

+2D

⊥

0.53 − 0.59

[XI]

⊥

=5· 10

−6

||C



=1· 10

−5

0.53 − 0.59

[XV ][XV II]

Pd self- Polycrystals 1.1 1.17 · 10

−4

single crystal

diﬀusion 99.95% [XV III][XV III]0.71 − 0.84 [XIX]

0.57 − 0.715 [XX]

Pd self- 001 tilt 1.07 6.26 · 10

−5

diﬀusion and twist grain [XXIV ][XXIV ]

boundary

99.999 at%

Sn self- polycrystals 0.99 7.8 · 10

−5

single crystal

diﬀusion 99.99% [XXI] ⊥ C

0.304 − 0.362

||C

0.321 − 0.329

3.5 Experimental Results 263

TABLE 3.8

Parameters of Grain Boundary Diﬀusion

Metal H

[eV] (δD

)

/s] V

∗

/Ω

Ag self- 0.92 5.76 · 10

−15

diﬀusion

[I]

Ag self- 1.05 2 · 10

−16

diﬀusion

[II]

Ag self- 0.67 1.16 · 10

−16

1.09

diﬀusion

[III]

Ag self-

diﬀusion

Al-Zn 0.54 [V III]3.1 · 10

−15

[V III]0.8 − 1.08 [IX]

0.52 ϕ =32

◦

0.87 ϕ =37

◦

111 tilt grain boundary [XI]

Au self- 0.88 [XIV ]3.1 · 10

−16

[XIV ]

diﬀusion

Cd self- 0.48 [XV I]3.35 · 10

−14

diﬀusion

Pd self- 0.68 [XV III]8.17 · 10

−14

diﬀusion

Pd self- Twist grain boundary [XXV ]

diﬀusion 0.35

tilt grain boundary

ϕ =30

◦

0.2

Sn self- 0.43 [XXIII]3.22 · 10

−15

diﬀusion

I — Hoﬀmann RE, Turnbull D. J. Appl. P hys., 22:634, 1951.

II — Turnbull D, Hoﬀmann RE. Acta Metall., 2:419, 1954.

III — Kaigorodov VN, Klotsman SM, Timofeev AN, Trakhtenberg IS.

P hys. Met. Metall., 25:910, 1968.

IV —Rein G, Mehrer H. Phil. Mag., A45:767, 1982.

V—BeyelerM,These Universit´eParis, 1968.

VI — Beke DL, Godeny I. Phil. Mag., A47:281, 1983.

VII—ErdelyiG,LojkowskiW,BekeDK,G¨odeny I, Kedves JL. in

Diﬀusion in Metals and Alloys, Kedves FJ, Beke DL,

editors. Aldermannsdorf, p. 398, 1983.

VIII — G¨odeny I, Beke DK, Kedves FJ. T rans. Japan. Inst. Metals

(suppl.), 27:525, 1986.

IX — Erdelyi G, Lojkowski W, Beke DK, G¨odeny I, Kedves JL. Phil.

Mag.,A56 : 673, 1987.

X—OvsienkoDY,ZasimcukIK.Phys.Met.Metall., 10:743, 1960.