Gottstein G., Shvindlerman L.S. Grain Boundary Migration in Metals: Thermodynamics, Kinetics, Applications

Подождите немного. Документ загружается.

304 3 Grain Boundary Motion

D’

/s]

-17

-18

-19

-20

0 5 10 15 2520

V* [cm

/mol]

FIGURE 3.122

Dependence of the product under zero pressure on activation volume at 161

◦

an example, the case of grain boundary motion under a constant driving force

P . The rate of reduction of the free energy of the system dG/dt,

= −vP (3.205)

where v = m

P is the velocity of grain boundary motion, m

the grain bound-

ary mobility. Accordingly,

= −vP = −m

(3.206)

and

= m

−

∗

; m

= e

∗

(3.207)

where G

∗

= E

∗

−TS

∗

+pV

∗

= H

∗

−TS

∗

is the Gibbs free energy of activation.

Let us consider the extremum of the function in Eq. (3.206) with respect

to an arbitrary state parameter λ:

dλ





dλ



−m



= 0 (3.208)

and since P is independent of λ

dλ

) = 0 (3.209)

With λ = λ

at the maximum of dG/dt and using Eqs.(3.206) and (3.207)

dλ

∗

− TS

∗

)

λ=λ

= 0 (3.210)

3.7 Compensation Eﬀect in Grain Boundary Motion 305

Again we obtain the compensation temperature



∗



λ=λ

(3.211)

As a result, the CE is in agreement with the principles of nonequilibrium

thermodynamics and yields the previously derived CT.

It is noted that there are several atomistic approaches of the activation

process. Either the energy dissipation into the adjoining ﬁnite volume is con-

sidered [384]–[386], or, alternatively, the transition state is examined as a

heterophase ﬂuctuation [387].

3.7.4 Applications

3.7.4.1 The Island Model of Grain Boundary Migration

To reveal the meaning and signiﬁcance of the CE and the CT we will study

a simple model system, namely grain boundary migration according to the

“island” model as proposed by Mott long ago [162]. The model assumes that

groups of n atoms “melt” on the side of the vanishing grain and become

attached to the side of the growing grain. The activated, metastable state is

identiﬁed with a frozen liquid state. This permits one to determine the entropy

and enthalpy of activation, namely

∗

= nL (3.212)

where L is the heat of melting per atom, and T

is the melting temperature.

The velocity v of the grain boundary according to this model reads

v = bνn

ΔG

exp



∗



exp



−

∗



(3.213)

where b is the atomic spacing and ν the Debye frequency.

It is obvious from Eq. (3.213) that the model complies with the compensa-

tion eﬀect: the enthalpy of activation is proportional to the activation entropy.

∗

= T

∗

(3.214)

and, therefore,

∗

= T

(3.215)

An identical result can be obtained in terms of irreversible thermodynamics

according to Eq. (3.211).

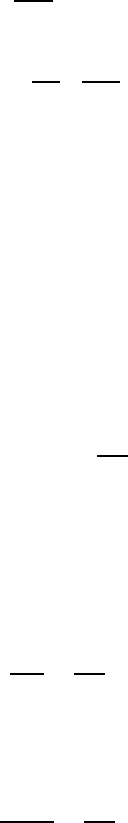
306 3 Grain Boundary Motion

3.7.4.2 Brown-Ashby Relations

Brown and Ashby [388] analyzed diﬀusion data for a wide range of solids

(metals and ceramics) and, as a result, found three correlations for a given

structure and bond type

D (T

)=κ

(3.216)

∗

= κ

(3.217)

and

∗





(3.218)

where κ

and κ

are constants, which in ﬁrst order are independent of the

pressure p; T

is the melting point at atmospheric pressure and k is the

Boltzmann constant.

We will show that Eqs. (3.216)–(3.218) are in full agreement with the con-

cepts of the CE as developed above [389]. If “for a given structure and bond

type” [388] the compensation eﬀect is obeyed, the compensation tempera-

ture necessarily coincides with the melting point, as for pure elements not

undergoing a phase transition in solid state, T

is the only temperature for

a ﬁrst-order phase transition in the temperature range discussed. Then, in

accordance with Eq. (3.191) we obtain for bulk diﬀusion

∗

= kT

ln D

+ β (3.219)

and at T = T

D (T

)=e

−

(3.220)

Apparently Eq. (3.220) exactly corresponds to the empirical relation given by

Eq. (3.219). We shall not discuss Eq. (3.217), which is a special case of the more

general relation (3.218). Most interesting is the third relation, Eq. (3.218). Let

us consider this relation in terms of the “activation-barrier-phase.” The change

in the transition point (compensation temperature T

) with pressure p is given

by the Clausius-Clapeyron equation

ΔV

ΔS

(3.221)

With

ΔV = V



− V

= V

∗

and ΔS = S



− S

= S

∗

(3.222)

we obtain

∗

(λ)

∗

(λ)

(3.223)

Since

∗

(λ)=E

∗

(λ) (3.224)

3.7 Compensation Eﬀect in Grain Boundary Motion 307

Eq. (3.223) can be rewritten as

∗

· T

∗

(3.225)

If the compensation temperature coincides with the melting point we arrive

at the Brown-Ashby relation

∗

(3.226)

Therefore, the Brown-Ashby relation can be considered a direct consequence

of the CE [389].

3.7.4.3 Impact of the CE on Thermally Activated Processes

Fig. 3.50 gives the measured rate of boundary migration vs. the misorien-

tation angle about a common 111 tilt axis [264]. The maximum velocity

is attained for a misorientation angle of ∼ 41

◦

. Over many years this result

worried scientists (including the authors themselves [390]). The point is that

close to the 41

◦

111 tilt grain boundary there is the special grain boundary

Σ7: 38.2

◦

111 with apparently high mobility and low activation energy of

migration [190, 275, 280, 299]. Therefore, the 41

◦

111 boundary was tacitly

assumed to represent a scatter of the Σ7 boundary. Nevertheless, numerous

growth selection experiments provided strong experimental evidence that the

maximum mobility was attained at misorientation angles above 40

◦

, i.e. close

to 41

◦

and not 38.2

◦

The misorientation dependence of activation enthalpy for migration of 111

tilt grain boundaries in the vicinity of the special grain boundary Σ7 (38.2

◦

)

as obtained from bicrystal experiments [190] is given in Fig. 3.123. Obviously,

the activation enthalpy is at maximum for a misorientation angle close to 41

◦

However, the misorientation dependence of the preexponential factor behaves

the same way, i.e. attains a maximum for 41

◦

misorientation (Fig. 3.124). In

fact, the CE with a CT of ∼ 450

◦

C (Fig. 3.125) causes the grain boundaries

with the lowest activation energy to be most mobile at T<CT,whereasfor

T>CTthe opposite is the case (Fig. 3.126). As a result, due to the CE,

which boundary moves fastest depends on the temperature range (relative

to CT), and this reconciles the contradiction between recrystallization and

growth selection experiments mentioned above.

As a general rule the compensation temperature divides the temperature

range into two regimes with diﬀerent relations between the magnitude of re-

action rate and energy of activation. When the experiments are conducted

below T

, then the processes with low energies of activation prevail. The re-

verse is also true; if the measurements are taken above T

, then the processes

with high energies of activation dominate the kinetics (Fig. 3.127).

The example given above also elucidates another consequence of the CE,

namely the drastically mitigated inﬂuence of the activation enthalpy. For

308 3 Grain Boundary Motion

H [eV]

2.3

2.5

2.1

1.7

1.9

1.3

1.5

1.1

36 4038

42 44

[deg]

FIGURE 3.123

Activation enthalpy H

for migration of 111 tilt grain boundaries as a

function of misorientation angle ϕ for two diﬀerent aluminum charges: Al I -

0.4 ppm of impurity; Al II - 1.0 ppm of impurity.

36 37 38 39 40 41 42 43 44

[deg]

[

]

36 37 38 39 40 41 42 43 44

/s]

36 38 40 42 44

[deg]

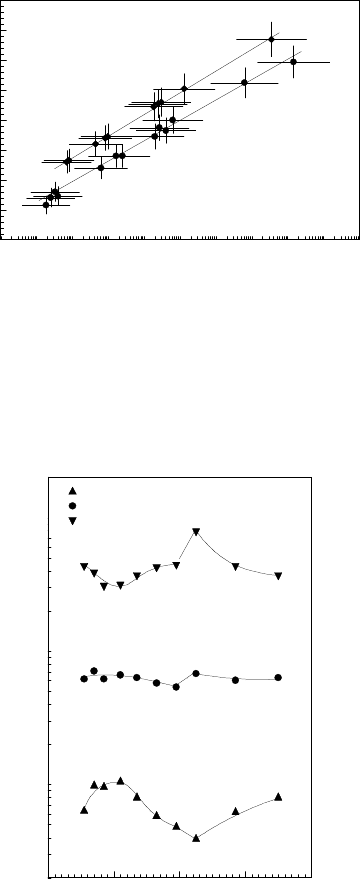
FIGURE 3.124

Reduced mobility preexponential factor A

of 111 tilt grain boundaries as

a function of misorientation angle ϕ for two diﬀerent aluminum charges: (• -

Al I;  -AlII).

3.7 Compensation Eﬀect in Grain Boundary Motion 309

[eV]

2.6

2.2

1.8

1.4

1.0

/s]

FIGURE 3.125

Dependence of migration activation enthalpy H

on the preexponential re-

duced mobility factor A

for the investigated 111 tilt grain boundaries in

high-purity aluminum of two diﬀerent charges: (• -AlI; -AlII).

430°C

485°C

540°C

/s]

430°C

485°C

540°C

-7

-8

-9

[deg]

38 40 4442

FIGURE 3.126

Misorientation dependence of grain boundary reduced mobility A for 111

tilt boundaries in Al II at diﬀerent temperatures.

310 3 Grain Boundary Motion

In m

1/T

FIGURE 3.127

Schematic sketch demonstrating the impact of the CE on grain boundary

mobility m above and below the CT. (H

∗

; m

;

T>T

: m

; T<T

: m

instance, in the case of two diﬀerent 111 tilt grain boundaries (Σ7 and

40.5

◦

111) in Al the activation enthalpies for grain boundary migration are

∼ 1.24 eV and 2.1 eV, respectively. If we take into account the diﬀerence of

the activation enthalpy only, then at 480

◦

C the mobilities of the two bound-

aries would diﬀer by six orders of magnitude, while, in reality, due to the CE,

they diﬀer by not more than a factor of 3!

However, very often conclusions are drawn only on the basis of the mag-

nitude of the activation energy. For instance, on this basis it is contended a

small amount of impurities (0.001% Mn) in Al reduces the rate of boundary

migration by many orders of magnitude (up to 10

times) [390, 391]. Be-

cause of the CE this is very unlikely to happen and has never been observed.

In essence, the compensation eﬀect controls the kinetics of the processes (at

least, interfacial reactions), restricting and compensating the inﬂuence of the

involved activation parameters, in particular of the activation enthalpy.

3.7.4.4 The CE in Thermally Activated Bulk Processes

The CE is not restricted to interface phenomena. Brief mention has already

been made of CE observations on bulk activation processes [336]–[338]. But

nowhere is the role of the CE as important as in grain boundary activation

processes. As an example let us consider bulk diﬀusion. In this case the preex-

ponential factor is predicted by Zener’s theory [392], which assumes that the

Gibbs free energy G

∗

of an atom in the transition state — i.e. in the saddle

3.8 Mechanisms of Grain Boundary Migration 311

point conﬁguration — is deﬁned by the work of elastic deformation

∗

με

(3.227)

where ε

is some eﬀective elastic strain, μ the relevant elastic modulus [392].

Since G

∗

is a free energy, the corresponding entropy

∗

= −



∂G

∗

∂T



(3.228)

and, taking into account the very weak temperature dependence of the elastic

modulus μ

∗

∼

−G

∗

d (μ/μ

)

= −H

∗

d (μ/μ

)

(3.229)

where G

∗

= H

∗

is the Gibbs’ free activation energy and enthalpy and μ

the

shear modulus at 0K, respectively.

Introducing χ = d(μ/μ

)/d(T/T

), where T

is the melting temperature of

the solvent: S

∗

∼

(χH

∗

)/(T

). According to Zener’s theory the preexponen-

tial factor for bulk diﬀusion can change by less than 2–3 orders of magnitude.

This is negligible compared to the 7–10 orders of magnitude (!!) for grain

boundary diﬀusion or migration. It is emphasized again that this large vari-

ance in the preexponential factor is a consequence of the collective nature of

grain boundary processes. This is why the CE plays such an important role

in interfaces and especially grain boundary kinetics.

3.8 Mechanisms of Grain Boundary Migration

In Sec. 3.1 we mentioned that there is actually no theory of grain bound-

ary migration and hitherto, we have no detailed information on the atomic

mechanism of grain boundary migration, except from preliminary results of

molecular dynamics computer simulations [309] or high-resolution TEM stud-

ies of boundary migration [393]. Because of the importance of this issue to

the major topic of this text, we at least want to review and critically assess

proposals made in the past.

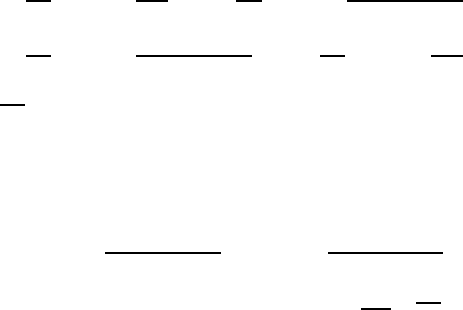
Early models [162, 178] of grain boundary structure assumed that the

grain boundary comprised a certain volume of thickness δ  b, i.e. much

broader than the spacing of atoms in the adjacent lattices, in other words

a wide boundary (Fig. 3.128). Corresponding phenomenological theories of

grain boundary motion have to consider that for steady-state motion the

three ﬂuxes

= j

(3.230)

312 3 Grain Boundary Motion

where j

is the ﬂux of atoms detaching from the consumed crystal, j

is the

ﬂux of atoms attaching to the growing crystal and j

= v/Ω

is the convec-

tion ﬂux in the boundary, i.e. a ﬂux of atoms that an observer attached to the

boundary would see. The attachment and detachment processes will be ther-

mally activated and may occur in a speciﬁc respective process (Fig. 3.128b)

= c

ν exp



−



− c

ν exp



−

+ P Ω



(3.231)

= c

ν exp



−

− P Ω



− c

ν exp



−



where c

are geometrical constants, G

the activation free energy of the

diﬀusive atomic motion. Assuming similar structural conditions on both shores

of the boundary: c

= c

, c

= c

yields c

= c

and with Ω

≈ b

v = c

bν



exp



−

− P Ω



− exp



−

+ P Ω



(3.232)

∼

−

· P

which is the fundamental equation already derived in Sec. 3.1.

The detachment and attachment process may be composed of several steps,

each of which may be associated with a speciﬁc ﬂux equation, which will com-

plicate the system of Eq. (3.231) but yield a similar solution to contain the

activation energies for the elementary steps considered. Also, vacancies may be

involved in the diﬀusion process at the boundary edges so that the boundary

vacancy concentration can be introduced in Eq. (3.232). Such an approach

allows us to introduce crystallography in the modeling of grain boundary

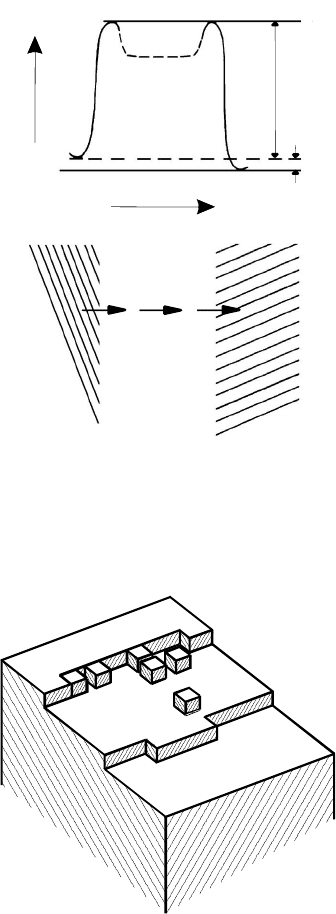
migration. This was ﬁrst proposed by Gleiter [177], who treated grain bound-

ary migration like an evaporation/condensation process on the internal crys-

tal surfaces (Fig. 3.129) and, therefore, tacitly assumed the existence of a

wide grain boundary. This concept can, in principle, account for the observed

anisotropy of grain boundary migration. Unfortunately, this theory lacks pre-

dictive power since most involved crystallographic parameters are unknown.

A more serious objection to the theory, however, is the assumption of a wide

grain boundary, which is in obvious contradiction to the narrow structure of

real grain boundaries observed (Chapter 2).

Mott [162] assumed in his theory of boundary migration (Island model)

that the boundary contains small patches of perfect crystal structure which

become detached and attached to the crystal surfaces by partial melting and

solidiﬁcation processes. The migration process can be modeled in analogy to

Eq. (3.232), except that the free activation energy is the energy of melting of a

cluster of n atoms and correspondingly the attachment of the island will move

the boundary by a distance nb. While this model is also based on unrealistic

3.8 Mechanisms of Grain Boundary Migration 313

free energy

boundary

distance

lattice 1 lattice 2

(a)

(b)

free energy

boundary

distance

lattice 1 lattice 2

(a)

(b)

FIGURE 3.128

Wide grain boundary (schematically); (a) free energy barrier; (b) ﬂuxes across

the boundary.

FIGURE 3.129

Model of grain boundary motion according to Gleiter [177]. Atoms are re-

moved from ledges on the surface of the shrinking grain and become attached

to ledges on the growing grain surface.