Gottstein G., Shvindlerman L.S. Grain Boundary Migration in Metals: Thermodynamics, Kinetics, Applications
Подождите немного. Документ загружается.


314 3 Grain Boundary Motion
assumptions of the boundary structure and does not incorporate boundary
crystallography, it is the first attempt to describe boundary migration as a
group motion of atoms. In Sec. 3.5 we reported the frequent observation of
high activation energies and large activation volumes of boundary migration
which are very difficult to reconcile with a single atom hopping motion as
a mechanism of boundary migration. Rather, the measured large activation
parameters hint at collective or cooperative motion of atomic groups. Never-
theless, in spite of their interesting approaches to account for specific exper-
imental observations, models based on a wide grain boundary structure are
unacceptable since there is unambiguous evidence that boundaries are narrow
and not wide (Chapter 2).
The rate theory of boundary migration for narrow boundaries is commonly
reduced to a single diffusive step as derived in Sec. 3.1 to yield Eq. (3.232)
for the migration rate. Such an approach cannot account for the observed
orientation dependence of activation energy and activation volume, since no
grain boundary structure is taken into account.
Substantial progress in the understanding of grain boundary phenomena
was achieved from the geometrical models of grain boundary structure, pre-
dominantly the CSL model (Chapter 2). With regard to grain boundary mo-
tion the CSL theory provided two important details. First, as already pointed
out by Kronberg and Wilson [394], low Σ CSL boundaries are expected to
segregate less and, therefore, are less affected by impurity drag. Second, non-
structural — or extrinsic — secondary grain boundary dislocations (SGBD)
cause steps
12
on the boundary at the dislocation cores (Fig. 3.130). The dis-
placement of an SGBD along the boundary — an SGBD can only exist in
the boundary — is associated with the displacement of the step, which is
equivalent to the displacement of the boundary (perpendicular to its plane).
The model is particularly attractive for grain boundary migration during re-
crystallization, because it conveniently unifies the process of dislocation de-
composition in the grain boundary and the process of grain boundary mi-
gration [395]–[397]. Since the glide motion of dislocations is fundamentally
associated with a shear deformation, the process of SGBD motion results in
a combined migration and sliding process of the grain boundary. However,
during recrystallization and grain growth no macroscopic shape changes are
observed. Thus we have to assume that the sum of shears is zero or, cor-
respondingly, that the total Burgers vector strength is zero. The attractive
feature of this concept is that it easily predicts orientations of rapid growth.
This is the case if the threshold of thermal activation is low, for instance, for
SGBDs moving in the grain boundary by simple glide. Even if the Burgers
vector is parallel to the grain boundary plane, SGBD glide motion will dis-
place the grain boundary, owing to the step in the boundary associated with
the core of the SGBD (Fig. 3.130). An example is the motion of a Σ3 coher-
12
Recently also referred to as disconnections [376].
© 2010 by Taylor and Francis Group, LLC

3.8 Mechanisms of Grain Boundary Migration 315
(a) (b)
b
b
[010]
[100]
FIGURE 3.130
Secondary grain boundary dislocation in a Σ5 tilt boundary [395]. Note step of
boundary at dislocation core. (a) Burgers vector parallel to boundary. Dislo-
cation is glissile along the boundary. (b) Burgers vector inclined to boundary.
Climb is necessary for dislocation motion in the boundary.
ent twin plane by glide of Shockley partial dislocations in fcc crystals. In fact,
Shockley partials are the SGBDs of the twin orientation.
Recent experiments, however, cast doubt on this dislocation concept of
grain boundary migration. Babcock and Balluffi [224] conducted in situ ex-
periments on grain boundary migration and sliding in thin-film Au bicrystals
in a hot stage of a TEM. The structure of the boundary (an orientation close
to Σ5) could be exactly defined in terms of SGBD. They confirmed the dislo-
cation model of combined grain boundary sliding and migration by correlating
successfully the amount of sliding and migration with the number of moving
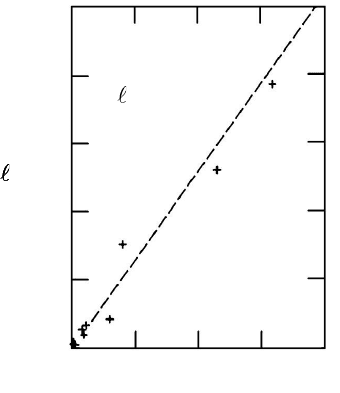
SGBD and their Burgers vectors (Fig. 3.131). However, this well-defined and
correlated motion constituted only a negligible part of the entire grain bound-
ary migration. Occasionally the authors observed jerky motion with very high
migration rate, but without any noticeable change in the dislocation struc-
ture of the grain boundary. The authors concluded from such results that the
normal process of grain boundary migration is not related to the motion of
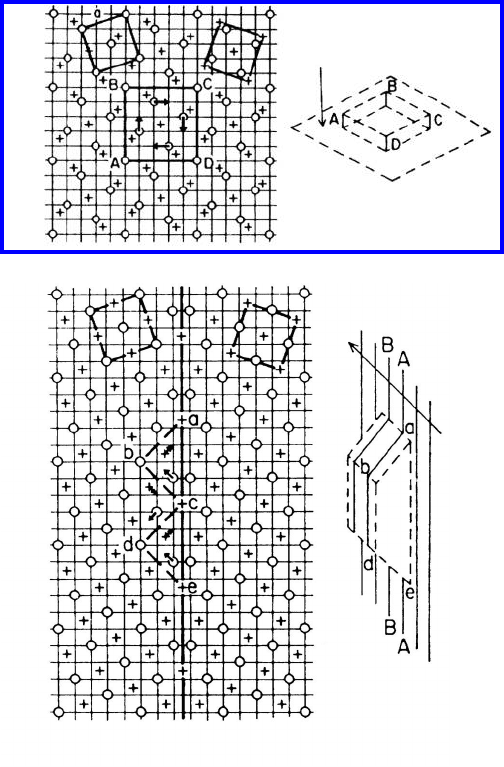
SGBD. Rather, they propose a shuffling mechanism of atoms for the migra-
tion process (Fig.3.132). Such a shuffling model would be supported by recent
computer simulations of the motion of a Σ5 boundary under the pressure of
its curvature. The study revealed cooperative motion of groups of atoms dur-
ing certain steps of grain boundary migration. The authors concede, however,
that this coordinated motion may be facilitated by the high degree of order in
the grain boundary and may be less likely in random grain boundaries which,
however, also have been observed to move very fast.
© 2010 by Taylor and Francis Group, LLC
316 3 Grain Boundary Motion
500 1000 1500 2000
B3
B6
B4
B5
N
0
0
50
100
150
200
250
= 0.129N [nm]
l
[nm ]
500 1000 1500 2000
B3
B6
B4
B5
N
0
0
50
100
150
200
250
= 0.129N [nm]
[nm ]
[nm ]
FIGURE 3.131
Observed boundary displacement due to slip of N secondary grain boundary
dislocations in a thin-film gold bicrystal [224].
The concept of grain boundary migration by coordinated movement of
atoms is not new and the current results do not substantiate a model of
cooperative motion beyond the state of conjecture. But the findings make it
obvious that a closer look at the movement of atoms during the process of
grain boundary migration will be necessary to gain a deeper understanding of
this seemingly so trivial, but in detail so complicated, process.
More recent molecular dynamics computer simulations on flat 100 twist
boundaries [309] have confirmed such cooperative processes, although the ac-
tual trajectory of atoms during boundary migration is very complex owing
to a high level of thermal activation in and close to the boundary causing
concomitant rapid diffusive motion and high defect (vacancy) concentration.
A more detailed analysis of such results is provided in Chapter 5.
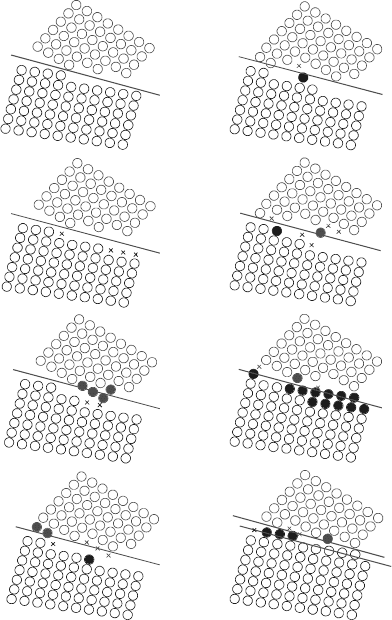
Finally, we should mention that there also have been attempts to observe
grain boundary migration in situ in an HREM. In fact, such a motion was
observed in thin-film bicrystals of Au. However, in analogy to the highly
perturbed boundary structure reported from molecular dynamics computer
simulations, the high resolution image of the atoms (columns) in the bound-
ary is blurred and prevents elementary steps of motion to be discriminated
(Fig. 3.133). However, the comparison of the atomic arrangement of the crys-
tal surfaces in the boundary definitely reveals that ledges on the boundary
are dismantled on one (shrinking) side and extended on the other (growing)
© 2010 by Taylor and Francis Group, LLC
3.8 Mechanisms of Grain Boundary Migration 317
(a)
(b)
(
α
)
(
α
)
(
β
)
(
α
)
[001]
(a)
(b)
(
α
)
(
α
)
(
β
)
(
α
)
[001]
FIGURE 3.132
Shuffling model of grain boundary motion as proposed by Babcock and Balluffi
for Σ5[001] twist boundary (a) ((α) The first planes of crystal 1 (0’s) and 2
(+’s)) and the same for Σ5 [001] tilt grain boundary (b) ((α) the first planes
of the crystals 1 and 2; (β) the view of the boundary edge) [224].
© 2010 by Taylor and Francis Group, LLC
318 3 Grain Boundary Motion
side of the boundary (Fig. 3.134).
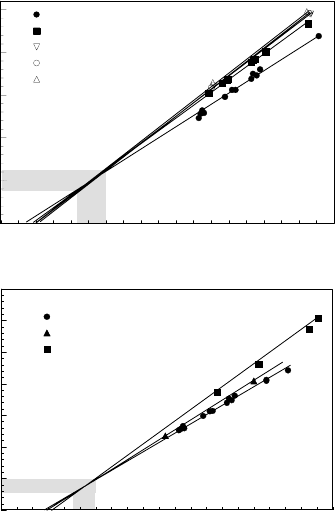
Eventually, the compensation effect opens up possibilities to look at the
mechanisms of grain boundary motion from quite a different perspective. The
compensation lines H(logA)for111 tilt grain boundaries in aluminum with
different total impurity content or different misorientation, respectively, are
given in Figs. 3.135a,b. Obviously, these lines have different slopes and con-
verge toward a range (H
∼
=
0.5eV,A
0
∼
=
10
−4
cm
2
s) which is shaded in
Fig. 3.135. Interestingly, these magnitudes of activation enthalpy and pre-
exponential factor correspond to the values predicted theoretically for grain
boundary migration under the assumption that the boundary moves by dif-
fusional jumps of individual atoms across the boundary [164]. We interpret
this result and the fact that the actually observed values of H
m
and A
0
are
much higher, as strong indications that grain boundaries move by the transfer
of groups of atoms across the boundary rather than by diffusional jumps of
single atoms. This approach is supported by the measurement of the acti-
vation volume of boundary migration as reported in Sec. 3.5.8 [304]. In fact,
Fig. 3.135 substantiates that a group mechanism is the intrinsic mechanism of
grain boundary migration, which would also be engaged for completely pure
material. The respective investigation [197] provides evidence that the preex-
ponential factor is only little affected by changing solute concentration, i.e.
for any impurity content the activation parameters A
0
and H are far higher
than any reasonable estimate for a single atom jump mechanism of boundary
motion.
Prompted by the results of Rath and Hu [230]–[233] who found a non-
linear relationship between grain boundary migration rate and driving force
(erroneously, as explained in Sec. 3.5.1), there have been various attempts
to account for this finding theoretically. The impurity drag and vacancy drag
theory already predict a nonlinear dynamics of grain boundary motion in very
dilute alloys, but only in a very narrow range of conditions which were un-
likely to be maintained experimentally. The only way to account for stable
nonlinear dynamics is a velocity-dependent mobility in Eq. (3.6), since grain
boundary motion is always a drift motion and thus, its velocity proportional
to the driving force, as shown in Sec. 3.1.
The grain boundary mobility can depend on velocity only if the migration
mechanism is affected by the migration rate. One possible mechanism is the
spiral growth mechanism as proposed by [399] in analogy to crystal growth.
The centers of the spirals are grain boundary screw dislocations which are as-
sumed to be decomposition products of crystal dislocations, absorbed in the
grain boundary during grain boundary motion. Accordingly, the spiral density
is proportional to the dislocation density, i.e. proportional to the driving force
v = m(P ) · P ∼ P
2
(3.233)
Indeed, spiraling grain boundary screw dislocations were observed experimen-
tally (Fig. 3.136).
While this spiral mechanism at least would account for a nonlinear grain
© 2010 by Taylor and Francis Group, LLC

3.8 Mechanisms of Grain Boundary Migration 319
0.24 s
0.00 s
0.88 s
1.24 s
1.64 s
1.76 s
2.28 s
2.40 s
FIGURE 3.133
Selected video frames of HREM images of a moving boundary in a thin-film
gold bicrystal.
© 2010 by Taylor and Francis Group, LLC
320 3 Grain Boundary Motion
0.00 s
0.24 s
0.88 s
1.24 s
1.64 s
1.76 s
2.28 s
2.40 s
FIGURE 3.134
Resolved atomic positions on video frames shown in Fig. 3.133. The boundary
moves first down and then back up. Filled circles denote newly attached atoms,
x indicates removed lattice sites. The two lines shown at 2.40 s represent the
initial and final positions of the boundary.
© 2010 by Taylor and Francis Group, LLC
3.8 Mechanisms of Grain Boundary Migration 321
0.4 ppm
1.0 ppm
3.6 ppm
4.9 ppm
7.7 ppm
<111>
<100>
<110>
0.4 ppm
1.0 ppm
3.6 ppm
4.9 ppm
7.7 ppm
H
m
[eV]
2.5
1.5
0.5
10
-10
A
0
[m
2
/s]
10
-8
10
-6
10
-4
10
-2
10
0
10
2
10
4
10
8
10
6
3.5
2.5
3.0
2.0
1.5
0.0
1.0
0.5
10
-10
10
-5
10
0
10
5
10
10
A
0
[m
2
/s]
<111>
<100>
<110>
H
m
[eV]
(a)
(b)
FIGURE 3.135
Compensation lines H(logA
0
) for various tilt grain boundaries in Al: (a) same
misorientation but different impurity content; (b) same impurity content but
different orientation.
© 2010 by Taylor and Francis Group, LLC
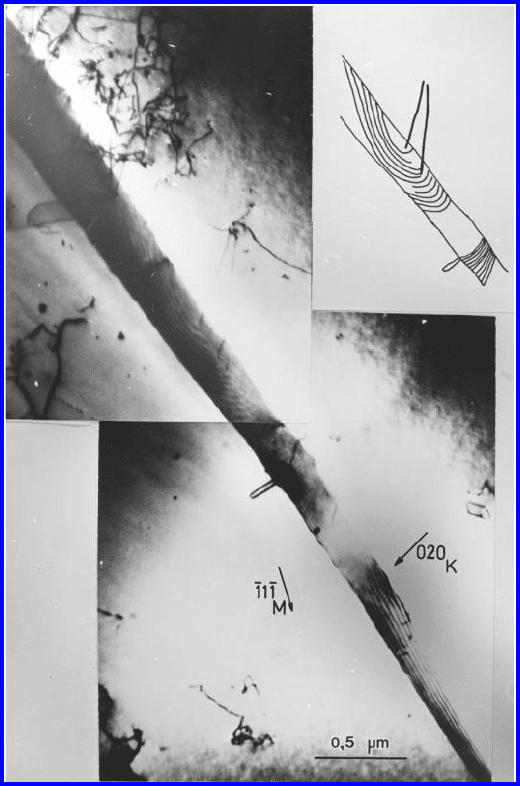
322 3 Grain Boundary Motion
FIGURE 3.136
Generation of a spiral SGBD source by interaction of a crystal dislocation
with a moving grain boundary in dynamically recrystallizing Cu at 930
◦
C
[398].
© 2010 by Taylor and Francis Group, LLC
3.8 Mechanisms of Grain Boundary Migration 323
boundary dynamics, all accurate measurements so far have ruled out the need
for such dependency. It is finally noted that the spiral mechanism is easily
combined with vacancy drag owing to the annihilation of the crystal disloca-
tions in the boundary, since the dislocation decomposition will provide both
free excess volume (vacancies) as well as secondary grain boundary screw
dislocations, i.e. the center of a growth spiral.
© 2010 by Taylor and Francis Group, LLC
