Gottstein G., Shvindlerman L.S. Grain Boundary Migration in Metals: Thermodynamics, Kinetics, Applications

Подождите немного. Документ загружается.

4.6 Triple Junction Drag and Grain Growth in 2D Polycrystals 375

or the wonderful engravings of Escher.

The driving force for grain growth is the excess free energy of grain bound-

aries — their surface tension. Under this driving force grain boundaries mi-

grate through the crystal. This motion leads to the shrinking of some grains

and growth of others but on average to an increase in the mean grain size.

Other examples of domain growth phenomena are antiphase domains and soap

froth. The described change in the grain microstructure conspicuously aﬀects

some of the physical, mechanical, and chemical properties of the materials.

A polycrystal is an inhomogeneous system, and the characteristic scale of

this inhomogeneity is the grain size

R. This quantity is of concern in a num-

ber of theoretical and empirical relationships and model considerations: the

Hall-Petch relation for plastic deformation, diﬀusion creep (Nabarro-Herring

and Coble relations), diﬀusivity, and so on. The dependence of

R on time

and the inﬂuence of diﬀerent factors on the grain size such as temperature,

impurity content, etc. are the most important issues of grain growth kinet-

ics. In many cases not only the characteristic grain size

R is important, but

more speciﬁc features of the system as well, e.g. grain size distribution, orien-

tation distribution, topological aspects of grain microstructure, the eﬀect of

the second-phase particles, voids, etc. It is well known that the major ther-

modynamic and kinetic properties of grain boundaries depend markedly on

the misorientation of adjacent grains and on the spatial orientation of the

boundaries (inclination) (see Chapters 1 and 3). In this chapter these aspects

of the problem will not be taken into account. Consideration and discussion

will be given in the framework of the so-called uniform grain boundary model

(to be explained below). The second distinctive property of this chapter is

that, contrary to other reviews and books (for instance [416]–[418]), special

consideration is given to the inﬂuence of grain boundary triple junctions and

quadruple points on grain growth.

The ﬁrst part of this section is dedicated to the grain growth in 2D subjects

— foils, thin ﬁlms, adsorbed phases, 2D phases, etc.

The second part addresses grain growth in 3D systems, the inﬂuence of

triple junctions and quadruple points on the kinetics of grain growth in such

a system and the generalized relation between the topological class of a grain

and the volume rate of change.

Finally, the kinetics of grain growth aﬀected by vacancy generation is con-

sidered. The reduction in grain boundary area in the course of grain growth is

accompanied by a reduction in the grain boundary excess free volume which,

in turn, can be viewed as a ﬂux of vacancies into the bulk of the sample, as a

cause of elastic stresses and plastic deformation, and may even lead to voids

and crack formation.

376 4 Thermodynamics and Kinetics of Connected Grain Boundaries

4.6.2 Topology of Grain Structures

The diﬀerent topological elements in a polycrystal are related by the Euler

theorem

−G + F − E + V = 1 (4.54)

where G, F , E and V are the numbers of grains, boundaries, triple junctions

and vertices. For each grain another version of Euler’s theorem holds

− e

+ v

= 2 (4.55)

where f

, e

, v

are the numbers of grain boundaries, triple junctions and

quadruple points (vertices) which are forming the ith-grain.

Important restrictions apply because of the conditions imposed on grain

boundary junctions; all lines of the junctions are triple lines and the points

are quadruple points. For a given grain this leads to the relation

=3v

(4.56)

From Eqs. (4.55) and (4.56) it follows that there is only one independent

parameter, for example, f

. At the same time grains with the same f

may be

topologically diﬀerent [416].

The topological structure of a polycrystal can be described by the mean

values

f,¯e,¯v

f =



i=1

(4.57)

¯e =



i=1

(4.58)

¯v =



i=1

(4.59)

Another important characteristic of the grain structure is the mean number

of vertices per boundary. Note that the average here is taken over the whole

ensemble of boundaries, not grains [416, 417]:

¯η =



i=1

(4.60)

This quantity relates to

f by the well-known Coxeter relation:

f =

6 − ¯η

(4.61)

There are more restrictions on polycrystal topology. For example, the relations

discussed above allow

f = 4 which is to say that all grains are tetrahedra.

4.6 Triple Junction Drag and Grain Growth in 2D Polycrystals 377

However, it is impossible to ﬁll space by tetrahedra and at the same time to

comply with the requirements of connectivity: all junctions are triple lines and

quadruple points. The second example is related to 2D grain growth under

the action of triple junctions. In this case, as will be shown, the grains should

be transformed to polygons with rectilinear grains boundaries. Unfortunately,

the requirements of the connectivity are diﬃcult to formalize.

The topological structure of 3D polycrystals is rather complex [401, 404,

419]. The structure of a 2D polycrystal is much simpler. The topology of a

2D grain is described by one scalar integer parameter n, for instance, by the

number of triple junctions n which belong to the grain or, what is the same,

by the number of adjacent grains. The parameter n is commonly referred to as

the topological class of a 2D grain. The Euler relation for a 2D arrangement

leads to

G − E − V = 1 (4.62)

where G, E and V are the number of grains, boundaries (lines) and triple junc-

tions (points), respectively. Since three grain boundaries meet at a junction,

and every grain boundary connects two junctions, we arrive at

3V =2E =¯nG (4.63)

where ¯n is the mean number of junctions per grain. For a representative

polycrystal (G  1) <n>= 6 as evident from Eq. (4.62) and the fact that

one grain boundary belongs to two grains. The second consequence is that

the minimal value of n is two because there is no grain with a simple triple

junction, which would require that a boundary border two regions of the same

grain.

4.6.3 Elementary Topological Rearrangements

The topological structure of a polycrystal changes in the course of grain

growth. These changes are very important: grain growth proceeds by a de-

crease in the total number of grains and thus, is connected with the loss of

grains and the corresponding topological rearrangements. Not only does the

area of each grain vary with time, but so does the value of its topological

parameter n. The elementary topological rearrangements of a 2D structure

are shown in Fig. 4.35. In accordance with Eq. (4.61) the loss of a grain is ac-

companied by the disappearance of two junctions and three grain boundaries

(Fig. 4.35) [409, 416]. Such grain switching is called compulsory. Besides the

compulsory switching other spontaneous rearrangements are possible. Their

occurrence essentially aﬀects the structure of a polycrystal and grain growth

kinetics. The shrinking of grains with n =2andn = 3 is completely deter-

mined (Fig. 4.35). For n = 4 there are two topologically alternative possibil-

ities and for n = 5 there are ﬁve possible ways (Fig. 4.35). A spontaneous

switching occurs when the length of a boundary shrinks to zero and an unsta-

ble fourfold junction is formed (Fig. 4.35). This junction splits into two new

378 4 Thermodynamics and Kinetics of Connected Grain Boundaries

(a)

(b)

113

(a)

(b)

113

FIGURE 4.35

Topological rearrangements in a 2D system due to grain vanishing (a) and

due to grain boundary switching (b). For n = 5 there are ﬁve possible conﬁg-

urations [416].

junctions connected by a new boundary. Eventually, two grains decrease their

topological class by one and two grains increase their topological class by one;

so the total number of grains, boundaries and junctions remains unchanged

after the switching.

For a 3D system the topological rearrangements are much more compli-

cated. Parallel to the vanishing of grains there is a large spectrum of rear-

rangements in which the number of grain boundaries and junctions change in

accordance with the Euler theorem.

4.6.4 Grain Growth Kinetics

In this paragraph we will consider the role of diﬀerent structural elements of

a polycrystal during grain growth.

The major structural elements of a polycrystal are the grain boundaries.

They are the main source of driving force for grain growth; their motion and

interaction deﬁne the mechanism of grain growth. The major grain boundary

parameters essential to this process are grain boundary surface tension γ

and grain boundary mobility m

. These parameters can diﬀer for diﬀerent

grain boundaries and depend on boundary inclination. The motion of a grain

boundary element is determined by the grain boundary shape in the close

proximity of the element.

Neglecting anisotropy the equation of grain boundary motion can be written

(Eq. (3.115)) as

v = −m

γκ = −A

κ (4.64)

4.6 Triple Junction Drag and Grain Growth in 2D Polycrystals 379

where v is the velocity of the normal displacement of the boundary element,

κ is the local curvature. Eq. (4.62) represents a nonlinear partial diﬀerential

equation of ﬁrst order in time and second order in space.

During their motion grain boundaries interact at triple junctions and

quadruple points. Let us restrict our consideration here to grain boundaries

and triple junctions (the inﬂuence of quadruple points will be considered

later). Then the velocity of triple junction motion can be represented as



= m





i=1

τ

−



r



(4.65)

where m

and γ



·r are triple junction mobility and line tension, respectively,

the vector



is directed normal to the junction and the unit vectors τ

are

directed along the adjacent boundaries. The vector r is the radius of the triple

line curvature. Relation (4.65) deﬁnes the boundary conditions for the equa-

tions of grain boundary motion (Eq. (4.64)). The vector relation determines

two conditions at any point of a triple junction. However, three grain bound-

aries are intersecting at the triple junction; in other words, we need three

boundary conditions. The third condition is of geometrical origin: it is the

requirement for three surfaces (grain boundaries) to intersect along one line,

the triple junction.

If the role of triple junctions is neglected, the boundary conditions may be

simpliﬁed to the condition of equilibrium of the dihedral angles between the

three intersecting boundaries



i=1

τ

= 0 (4.66)

In many cases grain growth is considered under the assumption that the triple

junction line tension is rather small while grain mobility is rather large, so for

suﬃciently large grains the eﬀect of triple junctions can be neglected. We will

discuss this issue in greater detail later. However, we would like to stress here

that even for a polycrystal with rather large mean grain size it is impossible to

avoid a contribution of triple junctions to grain growth kinetics: the vanishing

grains necessarily experience a stage with extremely small grain size.

A conﬁguration where more than three boundaries intersect along one line

is energetically unfavorable and thus unstable. It will split into several triple

junctions (see problem 2.3.4). We would like to remind the reader that this

holds in the framework of the uniform grain boundary model.

However, there is a stable conﬁguration where more than three grain bound-

aries meet. These are so-called quadruple junctions (points). In such a point

six grain boundaries, four grains and four triple lines meet. All other conﬁg-

urations of intersections are energetically unproﬁtable and, as a consequence,

unstable.

If the line tension of the triple junctions is neglected, the quadruple points

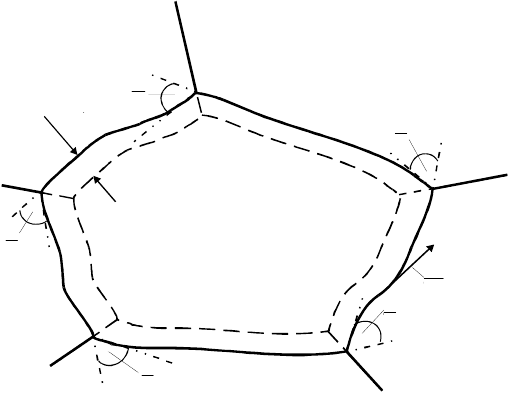
380 4 Thermodynamics and Kinetics of Connected Grain Boundaries

FIGURE 4.36

Deﬁnition of parameters for the eﬀect of triple junctions for a calculation of

the rate of grain area change.

do not introduce new boundary conditions — the equilibrium angles at the

triple junctions unambiguously determine the grain boundary conﬁguration

in the vicinity of the quadruple junctions [421]. In the case that the struc-

ture and energy of the triple junction line depend on the line direction the

line tension has to be taken into account for the equilibrium angles between

grain boundaries. It is stressed that the considerations made above relate to

stationary grain boundaries.

4.6.5 Uniform Grain Boundary Model and the Von

Neumann-Mullins Relation

For grain growth in a 2D system, Mullins [242] derived a fundamental relation,

which was originally formulated by Von Neumann for 2D soap froth [476]. The

respective model makes very fundamental assumptions, namely: (1) All grain

boundaries possess equal mobilities and surface tensions, irrespective of their

misorientation and the crystallographic orientations of the boundaries, the

so-called uniform grain boundary model; (2) the mobility of a grain bound-

ary is independent of its velocity; (3) the triple junctions do not aﬀect grain

boundary motion; therefore, the contact angles at triple junctions are always

in equilibrium and, due to the ﬁrst assumption, are equal to 120

◦

Let us consider a 2D grain with area S [242, 476]. In the time interval

4.6 Triple Junction Drag and Grain Growth in 2D Polycrystals 381

dt all points on the grain boundaries of the grain will be displaced normal

to the grain boundaries by the amount Vdt,whereV is the grain boundary

migration rate. Accordingly, the rate of change of the grain area S can be

expressed by

= −

Vd (4.67)

where d is an element of the grain perimeter. For grain growth

V = γm

κ ≡ A

κ (4.68)

where m

is the grain boundary mobility, γ is the grain boundary surface

tension, K is the local curvature of the grain boundary

K =

dϕ

d

(4.69)

where ϕ is the tangential angle at any given point of the grain boundary.

From Eqs. (4.67)–(4.69), it follows that

= −A

dϕ (4.70)

If the grain were bordered by a smooth line, the integral in Eq. (4.70) would

be equal to 2π. However, because of the discontinuous angular change at every

triple junction, the angular interval Δϕ = π/3 is subtracted from the total

value 2π for each triple junction. Consequently

= −A



2π −

nπ



(n − 6) (4.71)

where n is the number of triple junctions for each respective grain, i.e. the

topological class of the grain. Thus the rate of area change is independent of

the shape of the boundaries and determined by the topological class n only.

Grains with n>6 will grow and those with n<6 will disappear [242, 476].

Eq. (4.71) is referred to as the Von Neumann-Mullins relation.

What should especially be stressed is the generality of the approach con-

sidered and the versatility of the consequences; in part, the result expressed

in Eq. (4.71) does not depend on the shape of moving boundaries. The rate

of grain area changes along with the sign of the right-hand side of Eq. (4.71),

which is determined only by the number of the adjacent (neighboring) grains,

or, what is the same, by the topological class of the grain — the number of

triple junctions of the grain. That is why every attempt to revise either the

derivation of the Von Neumann-Mullins relation or its consequences attracts

considerable attention from materials scientists. However, Gusak and Tu de-

clared that they found an invalidity of the Von Neumann-Mullins (VN-M)

theorem [242, 476]. “To prove the invalidity of any theorem,” as the authors

wrote quite rightly, “it is enough to have just one example showing that it

382 4 Thermodynamics and Kinetics of Connected Grain Boundaries

is wrong.” For this purpose the authors considered the shrinkage of a regular

convex triangle, using the VN-M theorem and a “direct derivation,” to com-

pute the area change of a regular convex triangle [477].

The VN-M relation yields

= πm

γ, whereas the “direct derivation” of

the grain area change in the case of a shrinking regular convex triangle results

in:



π −

√



γ. Gusak and Tu attempted to explain the discrepancy

by considering in greater detail the motion of diﬀerent parts of a moving grain

boundary, which cannot, of course, replace the general and powerful VN-M

derivation. As can be seen, a correct derivation for a regular three-sided grain

only deviates on the order 3% from the VN-M result, and the diﬀerence is

thus clearly a second-order eﬀect.

Hunderi and Ryum [478] tried to solve the problem of the conﬁguration

considered by Gusak and Tu by numerical methods on the basis of the major

equations of the VN-M approach. Since their calculations were carried out in

the framework of the VN-M approach, the result is quite evident and pre-

dictable from the very beginning: the VN-M relation is correct.

Nevertheless, one issue remains open: what is the reason for such a discrep-

ancy?

A more sophisticated treatment of the phenomenon is given in [479]. The

reason for the discrepancy between the VN-M approach and the approach

of Gusak and Tu are the diﬀerent boundary conditions. Whereas the VN-M

approach associates the motion of a grain boundary element with the local

curvature when an element is displaced normal to itself, the approach put

forward by Gusak and Tu requires that the boundaries have a constant curva-

ture such that the contact angles at the triple junctions are in equilibrium. For

each displacement of a boundary, for instance a triangular grain, the curvature

has to be readjusted to account for equilibrium at the junctions. In fact, the

curvature will increase with progressing grain growth owing to the fact that

the grain shrinks. Therefore an additional adjustment of the grain boundary

geometry has to occur in order to maintain the proper curvature. In the VN-

M approach, such an adjustment is not enforced, since the boundary shape

can be arbitrary. Equilibrium at the junctions is established locally, and the

curvature driven grain boundary motion maintains or reduces the curvature

in contrast to the Gusak-Tu approach. In the Gusak-Tu approach two steps

of motion are involved, curvature driven growth and subsequent readjustment

of the curvature to re-establish constant curvature and junction equilibrium.

The VN-M approach considers only curvature driven growth and disregards

curvature adjustment at junctions as an eﬀect of second order. There is ac-

tually no physical principle that would require constant curvature, and the

Gusak-Tu approximation is a very special case determined entirely by geom-

etry, which however is not realized in nature.

Finally, it can be stated that the evolution of a “regular convex triangle”

during grain growth does not follow the scenario of Gusak and Tu [477],

namely the shrinkage as a self-similar regular triangle. If a regular convex tri-

angle is left to its own devices, it becomes an isosceles triangle and collapses

4.6 Triple Junction Drag and Grain Growth in 2D Polycrystals 383

as a triangle of irregular shape. Its state as a regular triangle is only one pos-

sibility among inﬁnitely many others. The correctness of the VN-M relation

cannot be judged from the behavior of a grain of a particular shape.

Thus, the phenomenon can be expressed like this. The conﬁguration de-

scribed and discussed by Gusak and Tu can appear in the course of grain

growth, however this is a conﬁguration without future, by increasing this

conﬁguration will be transformed to another, not so symmetrical conﬁgura-

tion (isosceles triangle) and, ﬁnally, collapse as a triangle of irregular shape.

Eq. (4.71) follows from the general Gauss-Bonnet theorem about the integral

of the Gaussian (total) curvature κ

. For two dimensions it coincides with the

Laplacian (mean) curvature κ

. Just this curvature determines the capillary

pressure and, as a consequence, the capillary driven grain boundary motion.

In three dimensions, however, these two curvatures are diﬀerent; even their

dimensionality is diﬀerent:

(4.72)

(4.73)

where R

and R

are the principal radii of curvature. That is why a direct

transfer of Eq. (4.71) to 3D systems is impossible. There have been attempts

to extend the results of the VN-M approach to a 3D situation. The successes

and failures of this attempt will be analyzed in further considerations.

4.6.6 Eﬀect of Triple Junction Drag on the Von

Neumann-Mullins Relation

Evidently, the existence of triple junctions dramatically aﬀects the kinetics

of grain growth. However, we will show below that the interaction of moving

grain boundaries with triple junctions also impacts our conception of mi-

crostructure evolution.

Let us consider the system shown in Fig. 4.5 [183, 403, 474]. This system

was analyzed comprehensively above. As can be seen from Fig. 4.5 this sys-

tem comprises three grains (three grain boundaries) with a common triple

junction. If a triple junction is mobile and does not drag grain boundary mo-

tion, then parameter Λ (Eq. (4.30)) tends to inﬁnity and the angle Θ → π/3,

i.e. the equilibrium angle at a triple junction in the uniform grain boundary

model. By contrast, however, when the mobility of the triple junction is rela-

tively low (strictly speaking, when m

a  m

then Θ → 0). It is particularly

emphasized that the angle Θ is completely deﬁned by the dimensionless pa-

rameter Λ, which, in turn, is a function of not only the ratio of triple junction

and grain boundary mobilities, but of the grain size as well. In the following,

we shall use the term “triple junction of low mobility” when we mean “small

value of Λ”.

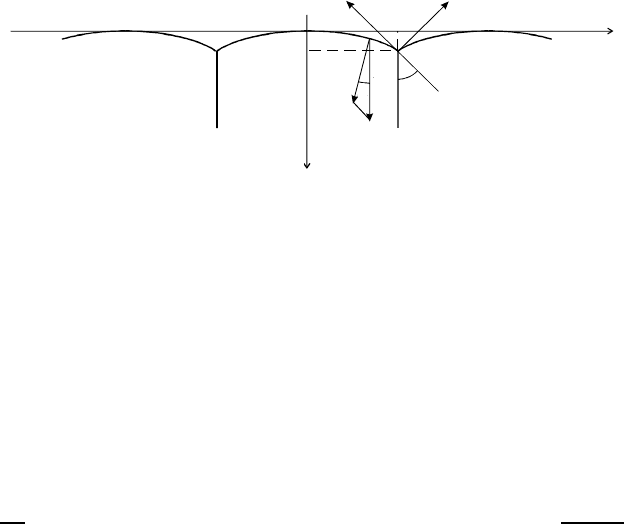
384 4 Thermodynamics and Kinetics of Connected Grain Boundaries

FIGURE 4.37

Conﬁguration of grain boundaries at triple junctions during steady-state mo-

tion for n>6.

One of the cornerstones of the VN-M relation is the assumption that the

triple junctions do not drag grain boundary motion. However, the fact that the

kinetics of triple junctions may be diﬀerent from the kinetics of the adjoining

grain boundaries aﬀects the kinetics of microstructure evolution during grain

growth, as formulated in terms of the VN-M relation.

Therateofareachangeforagrainwithn<6 can be expressed as

= −m

dϕ = −A

[2π − n (π − 2Θ)] = A

(π − 2Θ)



n −

2π

π − 2Θ



(4.74)

Since the limited mobility of the triple junction reduces the steady-state value

of the angle Θ as compared to the equilibrium angle, the shrinking rate of

grains with n<6 decreases, as obvious in the case when the mobility of the

triple junction becomes very low. In other words, for grains with n<6the

inﬂuence of the triple junction mobility slows down the process of grain struc-

ture evolution, decreasing the vanishing rate of grains with small topological

class (n<6).

For grains with topological class greater than 6 let us consider the steady-

state motion of a grain boundary system shown in Fig. 4.37 with the same

set of assumptions applied to the previous boundary system, namely, uniform

grain boundary properties and quasi-two-dimensionality [473]. The steady-

state motion of this system is determined by Eq. (4.25) only with diﬀerent

boundary and initial conditions



(0) = ∞ (4.75)



)=tanΘ

y(0) = 0

Thevelocityoftriplejunctionmotioncanbeexpressedas

= m

γ (1 − 2 cos Θ) (4.76)