Gottstein G., Shvindlerman L.S. Grain Boundary Migration in Metals: Thermodynamics, Kinetics, Applications

Подождите немного. Документ загружается.

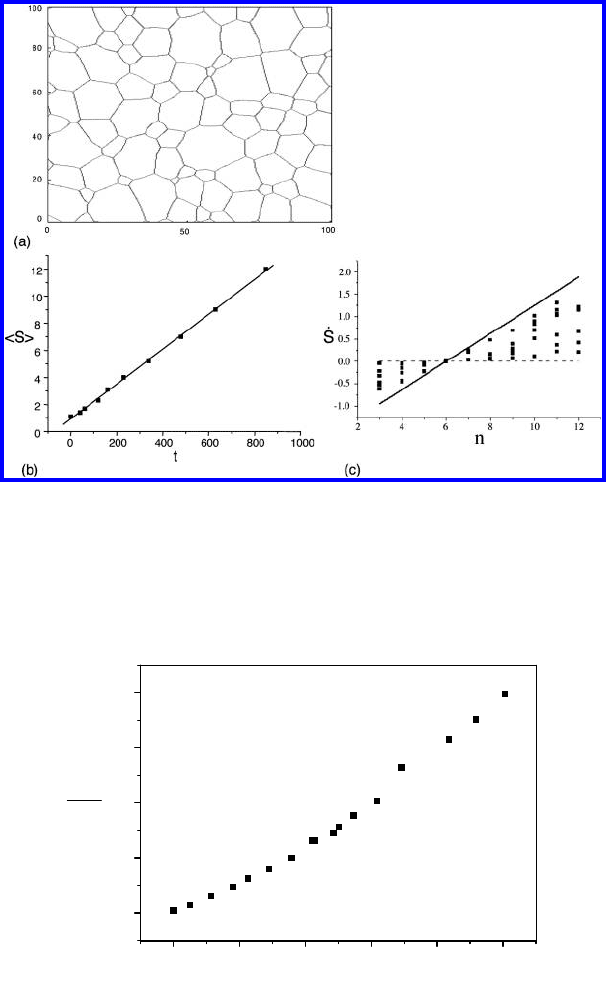
4.6 Triple Junction Drag and Grain Growth in 2D Polycrystals 395

FIGURE 4.41

Simulation results for 0.1 < Λ < 1.0. (a) Microstructure at S

=10.0; (b)

average area <S>vs. time t;(c)

S as function of n for 0.1 < Λ < 10. Solid

squares are the results of computer experiments; the line represents the Von

Neumann-Mullins relation.

0 1000 2000 3000 4000 5000

:0.15~1.5

:0.1

=0.3

()St

FIGURE 4.42

Grain size vs. time for 0.01 < Λ < 1.0.

396 4 Thermodynamics and Kinetics of Connected Grain Boundaries

to be controlled by purely boundary kinetics, aﬀected by triple junction drag,

rather the dependency

(Λ) clearly demonstrates that a ﬁnite triple junction

mobility fundamentally changes the character of the function. For a given n,

S(n) is not represented by a point anymore, but by a line (Fig. 4.43). There

are two issues which should be stressed. Firstly, a good agreement between

the computer experiments and theory is observed. Further, according to the

presented theoretical approach, Eqs. (4.82) and (4.84) perfectly describe in

close proximity to equilibrium, i.e., for rather large Λ, the inﬂuence of a ﬁnite

triple junction mobility on the rate of grain area change,

, given that all

Von Neumann-Mullins conditions, except the inﬁnite triple junction mobility,

are fulﬁlled. The expressions

n<6

≡

n<6

VNM

n<6

∼

6+Λ

√

2+Λ

√

n − 6

(4.90a)

n>6

≡

n>6

VNM

n>6

∼



1 −

πΛB



− 6

n − 6

(4.90b)

represent the ratio of the rate of grain area change for ﬁnite triple junction

mobility and for the pure Von Neumann-Mullins case. For the same value of

Λ, grains with n<6 deviate more strongly from pure grain boundary kinetics

than do grains with n>6. Therefore, grains with n = 4 are under triple

junction control (Fig. 4.43), whereas the growth of grains with n = 9 is still

governed by boundary kinetics (Fig. 4.43). In other words, triple junction drag

does not only slow down the rate of grain growth, but also changes the grain

microstructure of 2D polycrystals. This is also evident in experimental obser-

vations of grain growth in thin foils [445]. At the stage of the process where

triple junction inﬂuence becomes obvious, i.e. when the time dependency of

the mean grain size is linear, the grain size distribution becomes wider.

For grain growth strictly controlled by triple junction motion, theory pre-

dicts that the grain boundaries become ﬂat and that the grains approach the

shape of equilateral polygons. A polygon of arbitrary shape will be trans-

formed into an equilateral polygon, and any deviation from an equilateral

polygon will generate a force to restore the equilibrium shape. The only ex-

ception is a triangle, i.e. a grain of topological class n = 3 is always unstable

and bound to disappear. The computer simulations fully conﬁrm the theo-

retical predictions. Fig. 4.44 represents the grain microstructure developed

under triple junction kinetics. The grains are bordered by straight lines. The

ratio η =

i=1

curv

str

gives a quantitative measure of grain boundary curva-

ture, where L

curv

is the length of a curved boundary and L

str

is the distance

between the two corresponding triple junctions (Fig. 4.45). When Λ tends to

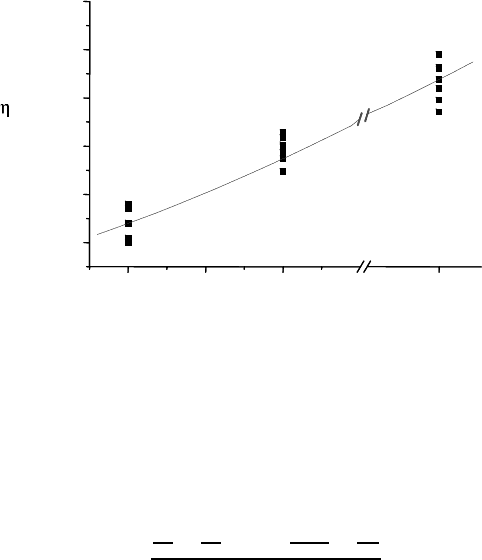
zero, η → 1 (Fig. 4.46).

To assess the theoretical prediction that under triple junction kinetics

all 2D grains of arbitrary shape become converted to equilateral polygons —

4.6 Triple Junction Drag and Grain Growth in 2D Polycrystals 397

5 10152025

-0.6

-0.5

-0.4

-0.3

-0.2

-0.1

5 10152025

0.70

0.75

0.80

0.85

0.90

0.95

0.0 0.1 0.2 0.3 0.4 0.5 0.6

-0.30

-0.25

-0.20

-0.15

-0.10

-0.05

0.00

0.0 0.2 0.4 0.6 0.8 1.0

-0.1

0.0

0.1

0.2

0.3

0.4

0.5

0.6

(a)

(c)

(d)

(b)

5 10152025

-0.6

-0.5

-0.4

-0.3

-0.2

-0.1

5 10152025

0.70

0.75

0.80

0.85

0.90

0.95

0.0 0.1 0.2 0.3 0.4 0.5 0.6

-0.30

-0.25

-0.20

-0.15

-0.10

-0.05

0.00

0.0 0.2 0.4 0.6 0.8 1.0

-0.1

0.0

0.1

0.2

0.3

0.4

0.5

0.6

(a)

(c)

(d)

(b)

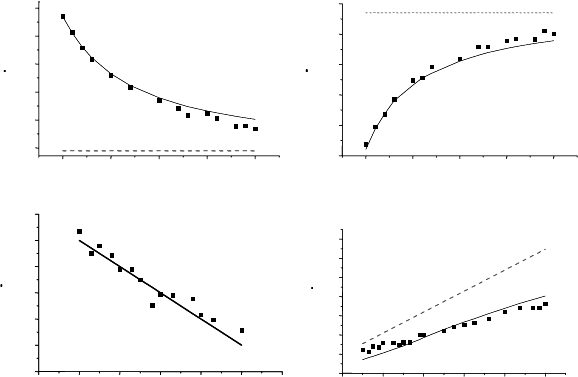
FIGURE 4.43

The rate of grain area change

S as a function of Λ (a) for grains with n =4.

Filled squares are the results of computer simulations. The solid line represents

the theoretical prediction of intermediate kinetics (Eqs. (4.30) and (4.71))

(5 < Λ < 25); the dotted line corresponds to the Von Neumann-Mullins

relation. (b) For grains with n = 9. The solid line represents the theoretical

prediction for intermediate kinetics (Eqs. (4.62) and (4.71)). The dotted line

corresponds to the Von Neumann-Mullins relation. (c) For grains with n =4,

and 0.1 < Λ < 1.0. The solid line represents the theoretical prediction for

triple junction kinetics (Eq. (4.89). (d) For grains with n = 9. The solid line

is the theoretical prediction for intermediate kinetics (Eqs. (4.62) and (4.71));

the broken line represents triple junction kinetics.

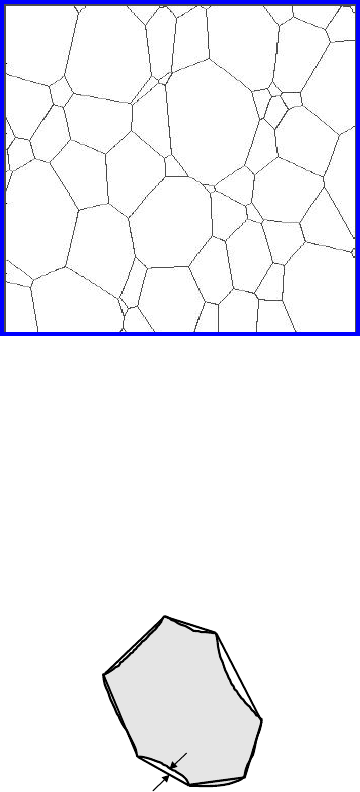
398 4 Thermodynamics and Kinetics of Connected Grain Boundaries

FIGURE 4.44

Simulation results for a 2D polycrystal at Λ ∼ 10

−4

. Microstructure at

=10.0.

curv

str

FIGURE 4.45

Measure of boundary straightness. The diagram explains how the value η was

measured.

4.6 Triple Junction Drag and Grain Growth in 2D Polycrystals 399

1.000

1.001

1.002

1.003

1.004

1.005

∞

-2

-4

log

1.000

1.001

1.002

1.003

1.004

1.005

∞

-2

-4

log

FIGURE 4.46

Computer simulation (ﬁlled squares up to S

= 10) and theoretical pre-

diction (solid line) of η(log Λ).

except for triangles — we deﬁne the parameter

+ ... +

n−1

(4.91)

where L

is the length of the i-th side of an n-sided grain. When the shape

of a grain approaches an equilateral polygon, β

→ 1. The only exception

is a triangle, which is unstable and has to disappear, i.e. β

should not con-

verge toward β

= 1. The behavior of β

with time was determined from the

computed microstructure, including β

(Fig. 4.47). Apparently for all studied

n-sided polygons β

→ 1, except for β

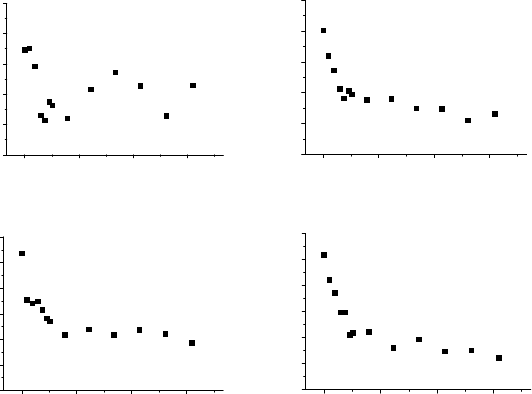
which changes randomly. Fig. 4.48

conﬁrms that such behavior of β

holds for triple junction kinetics only. The

value β

was measured up to S

= 10. As apparent from Figs. 4.47 and

4.48 a grain size ten times larger than the initial grain size was reached in a

much shorter time for boundary kinetics.

The function

S(n) for triple junction kinetics is presented in Fig. 4.49.

The curve is calculated according to Eq. (4.89) whereas the symbols repre-

sent simulation results. Except for the intrinsically unstable triangular grains

(n = 3), the theoretical predictions are in good agreement with the computer

experiment. We note that

S rises with n and approaches a limit (Eq. (4.89))

contrary to the predictions of the Von Neumann-Mullins relation.

The evolution of a 2D grain system with triple junctions was comprehen-

sively studied by computer simulations in [445, 446]. The results of [446] are

in good agreement with the approach discussed above.

400 4 Thermodynamics and Kinetics of Connected Grain Boundaries

0.0

3.0x10

6.0x10

9.0x10

1.00

1.05

1.10

1.15

1.20

1.25

0.0

3.0x10

6.0x10

9.0x10

0.9

1.0

1.1

1.2

1.3

1.4

0.0

3.0x10

6.0x10

9.0x10

0.9

1.0

1.1

1.2

1.3

1.4

1.5

0.0

3.0x10

6.0x10

9.0x10

0.9

1.0

1.1

1.2

1.3

1.4

1.5

0.0

3.0x10

6.0x10

9.0x10

1.00

1.05

1.10

1.15

1.20

1.25

0.0

3.0x10

6.0x10

9.0x10

0.9

1.0

1.1

1.2

1.3

1.4

0.0

3.0x10

6.0x10

9.0x10

0.9

1.0

1.1

1.2

1.3

1.4

1.5

0.0

3.0x10

6.0x10

9.0x10

0.9

1.0

1.1

1.2

1.3

1.4

1.5

FIGURE 4.47

Time dependence of β

for various n under triple junction kinetics (Λ ≈ 10

−4

up to S

= 10.

4.6 Triple Junction Drag and Grain Growth in 2D Polycrystals 401

-50 0 50 100 150 200 250 300 350

0.8

0.9

1.0

1.1

1.2

1.3

1.4

-50 0 50 100 150 200 250 300 350

0.9

1.0

1.1

1.2

1.3

1.4

1.5

-50 0 50 100 150 200 250 300 350

1.0

1.1

1.2

1.3

1.4

1.5

1.6

1.7

-50 0 50 100 150 200 250 300 350

0.9

1.0

1.1

1.2

1.3

1.4

1.5

1.6

1.7

-50 0 50 100 150 200 250 300 350

0.8

0.9

1.0

1.1

1.2

1.3

1.4

-50 0 50 100 150 200 250 300 350

0.9

1.0

1.1

1.2

1.3

1.4

1.5

-50 0 50 100 150 200 250 300 350

1.0

1.1

1.2

1.3

1.4

1.5

1.6

1.7

-50 0 50 100 150 200 250 300 350

0.9

1.0

1.1

1.2

1.3

1.4

1.5

1.6

1.7

FIGURE 4.48

Time dependence of the “rectilinearity” β

under grain boundary kinetics

(Λ  1) for S

=10.0.

24681012

-5.0x10

-5

0.0

5.0x10

-5

1.0x10

-4

1.5x10

-4

FIGURE 4.49

S vs. topological class n. Simulation results (ﬁlled squares) for Λ ∼ 10

−4

.The

solid line represents the dependency predicted by Eq. (4.89).

402 4 Thermodynamics and Kinetics of Connected Grain Boundaries

4.6.6.6 Grain Growth in a System with Boundary Junctions of

Finite Mobility: Experiments on Metallic Materials

Doubtlessly, the experimental observation of the eﬀects described above and

the general inﬂuence of grain boundary junctions on grain growth and evo-

lution in polycrystals especially in nanocrystalline materials is of great inter-

est. Unfortunately, there are only very few experimental investigations where

this attempt was undertaken. First we consider experimental studies of grain

growth in 2D Al foils [448].

As mentioned for junction-controlled grain growth all grains assume the

shape of a regular polygon, irrespective of their number of sides, except for

triangles. As shown in [441] a grain with the shape of a regular polygon re-

mains stable, i.e. does not undergo a shape change except for a triangular

shape.

Correspondingly, a 2D arrangement of grains with regular polygonal shape

would “freeze,” except if it contains triangular grains. The hexagonal structure

belongs to this set of stable geometries only if it is equilateral. On the other

hand, any other space-ﬁlling arrangement of regular polygons is a potentially

stable structure, if it can be attained

. The only exception is a triangle, and

any arrangement of regular polygons which contains at least a single triangle

would also be observed to behave in an unstable manner.

We reason that this phenomenon has important consequences for the de-

velopment of grain growth. Let us take a look at the evolution of a shrinking

grain in the course of grain growth. The topological class of such a grain

should be smaller than n = 6, naturally taking into account all corrections to

the Von Neumann-Mullins relation. As shown above the transition between

boundary and triple junction kinetics does not only depend on grain bound-

ary and triple junction mobility, but on the size of a grain as well. When the

size of a grain progressively diminishes there comes a time where boundary

kinetics is replaced by junction kinetics. This will happen to grains of the

topological class n =4orn = 5 which are bound to shrink even after such a

transition to triple junction kinetics. Grains of topological class n = 3 will col-

lapse without transforming into a regular polygon. Since the kinetics of triple

junctions are signiﬁcantly slower than the boundary kinetics, the four- and

ﬁve-side polygons will shrink, and eventually contract to a point although at a

markedly smaller rate. Experimentally this phenomenon will manifest itself in

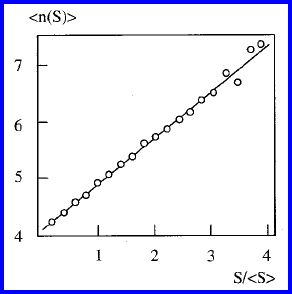
the mean value of the topological class of vanishing grains. In Fig. 4.50 exper-

imental data of grain growth in aluminum foil with 2D (columnar) structure

are presented, in terms of the grain size dependence of the mean topological

class <n>[448]. Extrapolation of this experimental dependence to zero area

yields the mean value of the topological class of vanishing grains. As can be

seen <n>(0)

∼

4.2, i.e. n = 4 is the smallest topological class to shrink in

We do not know whether space-ﬁlling topological arrangements of regular polygons exist

besides regular hexagons that satisfy the force equilibrium at junctions.

4.6 Triple Junction Drag and Grain Growth in 2D Polycrystals 403

FIGURE 4.50

Dependence of the mean topological class <n(s) > on “grain size” S/ < S >

(normalized by the average grain size) for pure Al [448].

a stable manner. In [429]–[432], the motion and geometry of connected (by

triple junctions) grain boundaries in 2D Al foils were investigated in situ in

an SEM with a specially designed heating stage. The experiments were car-

ried out on polycrystalline Al sheets of thickness 120 μm. The materials was

recrystallized to a mean grain size of 150 μm. This allowed us to realize an

approximately 2D microstructure.

EBSD measurements were carried out before and after in situ grain growth

experiments to determine the misorientation of the grains and to conﬁrm the

quasi-two-dimensionality of the grain structure. These EBSD checks were nec-

essary to ascertain that no grains from beneath surfaced and interfered with

the measurement.

The experiments were performed in a temperature range from 250 to 300

◦

The SEM was upgraded by a digital image scanning system, which collected

the images and saved them in AVI format. In post-processing the images were

analyzed by a special routine that measured the displacement of the triple

junctions and the vertex angles at the triple junctions.

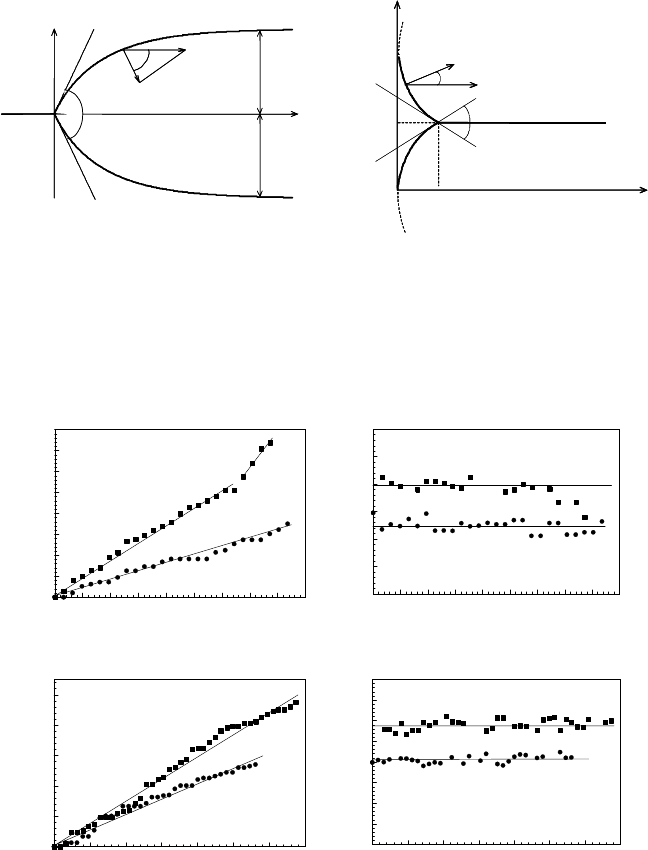
The authors tried to fulﬁl the main physical criteria, which were used as

a basis for the analysis of steady-state motion of the grain boundary system

with triple junction: uniform grain boundary model, the geometrical conﬁgu-

ration (Fig. 4.51), and the steady-state motion of the junction. Two speciﬁc

conﬁgurations were studied: for n<6andforn>6 (Fig. 4.51, Tables 4.8,

4.9).

Figs. 4.52 and 4.53 reveal steady-state motion of the investigated triple

junction in the course of grain growth triple junction displacement is linear

vs. time; vertex angles remain constant over the time of experiment.

The diagram obtained of the vertex angle Θ vs. the dimensionless criterion

404 4 Thermodynamics and Kinetics of Connected Grain Boundaries

a/2

GB III

GB II

GB I

GB II

GB III

(a) (b)

a/2

GB III

GB II

GB I

GB II

GB III

(a) (b)

FIGURE 4.51

The two basic conﬁgurations of a grain boundary system with triple junction

during steady state motion studied in [429].

0 50 100 150 200 250 300 350 400 450

time [s]

[

]

250 C

300 C

0 50 100 150 200 250 300 350 400 450

time [s]

100

120

[

]

250 C

300 C

(a)

(b)

0 100 200 300 400 500 600 700

time [s]

100

[

]

250 C

300 C

0 100 200 300 400 500 600 700

time [s]

100

120

140

160

[

]

250 C

300 C

0 50 100 150 200 250 300 350 400 450

time [s]

[

]

250 C

300 C

0 50 100 150 200 250 300 350 400 450

time [s]

100

120

[

]

250 C

300 C

(a)

(b)

0 100 200 300 400 500 600 700

time [s]

100

[

]

250 C

300 C

0 100 200 300 400 500 600 700

time [s]

100

120

140

160

[

]

250 C

300 C

FIGURE 4.52

(a) Displacement and vertex angle 2Θ vs. time for triple junction TP-S2 with

a conﬁguration of Fig. 4.51a at 250

◦

C and 300

◦

C. (b) Displacement and vertex

angle 2Θ vs. time for triple junction TP-S3 with a conﬁguration of Fig. 4.51a

at 250

◦

C and 300

◦