Gottstein G., Shvindlerman L.S. Grain Boundary Migration in Metals: Thermodynamics, Kinetics, Applications

Подождите немного. Документ загружается.

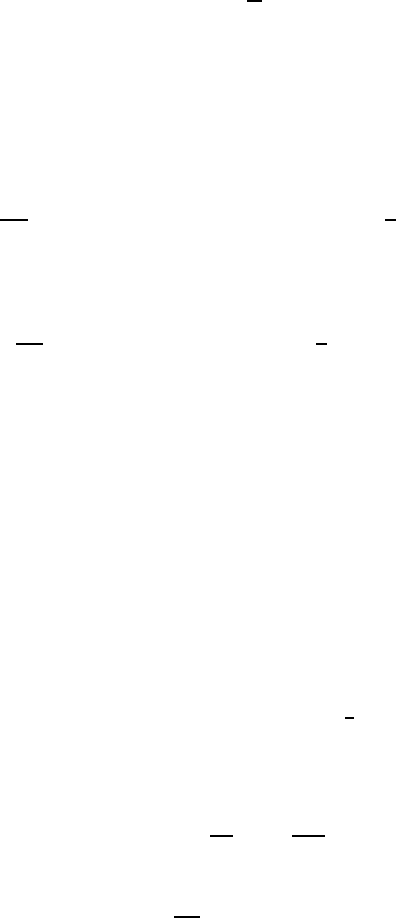
4.7 Grain Growth in 3D Systems 415

total curvature κ

. The average curvature ¯κ

can also be expressed as

¯κ





(ΔΘ) (4.106)

where ΔΘ gives the change in the direction of the tangent to the end of

the curve considered (Θ = arc tan(y



)). For a closed curve ΔΘ = ± 2π and

¯κ

= ±2π/2. In accordance with [553] ¯κ

is positive for the concave curve and

negative for the convex curve.

Then for a given grain

= −m



∂D

HdA = −2πm



L(D) −

e(D)



(4.107)

or if the volume of the grain is known at any time





−1/3

= −2πm



L(D) −

e(D)



· V

−1/3

(4.108)

As the Von Neumann-Mullins relation, the new relation (Eq. (4.108)) depends

only on the geometrical characteristics of the grain.

However, contrary to the Von Neumann-Mullins relation Eq. (4.104) is not

purely topological. The rate of grain volume change depends on the mean

width of the grain and the total length of the triple junctions. However, it

does not depend distinctly on the shape of the grain. If the right-hand side of

Eq. (4.104) is proportional to the grain size then the kinetics of grain growth

are governed by a parabolic law.

It is stressed that all approaches so far considered assumed (tacitly [545]–

[551], or explicitly [552]) that grain boundaries move slowly enough to main-

tain the equilibrium dihedral angles at triple junctions. In other words, the

mobility of all junctions is assumed to be inﬁnite.

For an isolated convex polyhedral grain with curved faces bounded by sharp

edges the total curvature κ

is equal to κ

ΔΘL +¯κ

S =2π

D where

is the average mean curvature of just the grain surfaces (faces), ΔΘ is the

complement of the average dihedral edge angle, S is the total area and L is

the edge length. Then

¯κ

2π



D −

ΔΘ

4π



(4.109)

For the particular case of polyhedra with ﬂat faces κ

is zero and the caliper

diameter

D is equal to

D =

ΔΘ

4π

L. Cahn’s equation can be considered a par-

ticular solution of the general Eq. (4.104). In what follows the approach based

on relation (4.104) will be called the Cahn-MacPherson-Srolovitz relation.

416 4 Thermodynamics and Kinetics of Connected Grain Boundaries

(a) (b) (c)(a) (b) (c)

FIGURE 4.60 (SEE COLOR INSERT FOLLOWING PAGE 424)

Conﬁgurations used for the simulation of the diverse analytical expressions

corresponding to (a) a 3-sided grain, (b) a tetrahedral grain and (c) a hexag-

onal prismatic grain. The grains surrounding these grains and forming the

granular aggregates are not shown. The case of the hexagonal prism is special

since it is surrounded by other hexagonal prisms and thus presents steady-

state motion of its grain boundaries [554].

4.7.2 Computer Simulations of 3D Grain Growth

4.7.2.1 Solitary Grains

In [554] a three-dimensional vertex model was utilized to study grain growth

in 3D systems and to analyze how the aforementioned approaches represent

reality.

Contrary to the 2D situation the details of grain growth in 3D systems can

be quantitatively studied only by computer simulations since the techniques

for continuous characterization of 3D grain structures are still at their infancy.

The problem was considered in two stages. Firstly, the grain growth of a

single grain was examined and the results were compared quantitatively with

analytical approaches developed by MacPherson and Srolovitz [552]. In the

second stage the kinetics of grain growth in 3D polycrystals obtained by com-

puter simulations were compared to analytical predictions [541, 542, 554].

Three simple singular grain shapes were considered in [554] (Fig. 4.60). Al-

though these conﬁgurations are unlikely to be found in a normal polycrystal

(the tetrahedron is an exception) their simplicity makes them a good subject

to test the diﬀerent approaches discussed above.

We would like to stress again that the Cahn-MacPherson-Srolovitz ap-

proach is the only one that considers the metrics of the grains, which change

dynamically in the course of grain growth. As a result this approach predicts

a non-constant time dependency of the normalized volume rate of change

(

−1/3

). All other models depend only on the topological class and thus

predict a constant value of (

−1/3

). Comparison of the Cahn-MacPherson-

Srolovitz approach with experimental results is somehow complicated because

the parameters of this approach have to be determined from the current ge-

4.7 Grain Growth in 3D Systems 417

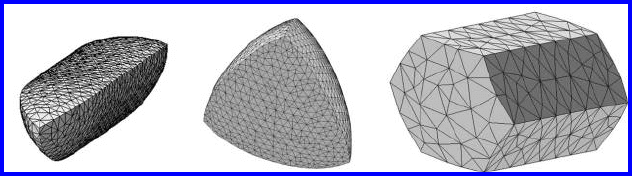
FIGURE 4.61

A hexagonal prismatic grain and the two dimensions a and d are shown [542].

ometry of the grains. A vertex model allows us to deﬁne all the parameters for

this calculation during the evolution of the volume of a grain. In the following

we will explain more comprehensively how the Cahn-MacPherson-Srolovitz

relation (4.104), (4.108) can be computed from the simulated microstructure

[554].

For this we consider the example of a hexagonal prismatic grain [542]

(Fig. 4.61)

L(D)=

2π



(4.110)

e(D)=



(4.111)

The term e(D) is the length of the triple junctions of a given grain and is

equal to the sum of the length of all triple lines N

of such a grain.

The term L(D) reﬂects the local variation of the surface with respect to

a ﬁxed reference. To better understand this we need to imagine that the

surface is also divided into very small surface elements. The normal to each

element of the surface dS characterizes its spatial orientation, which may

be diﬀerent from all other pieces of surface surrounding the element dS;the

angle β is known as the turning angle and represents precisely the variation

of one surface element with respect to another. The term e

in Eq. (4.110)

comprises the length of the junction between the dS elements. The sum over

all junctions n

corresponds to the mean width of the whole domain. The

orientation diﬀerence β across a triple junction corresponds to the external

dihedral angle which in the equilibrium is established by the surface tensions

of the adjoining grain boundaries. Another interesting feature of this term is

that it introduces implicitly the curvature of the surface in Eq. (4.104).

As an example in Fig. 4.61 two new variables, a and d, deﬁne the dimensions

of the grain: d is the length of the longitudinal triple line grain and a is the

length of a side of the hexagonal cross section; the curvature of the triple line

418 4 Thermodynamics and Kinetics of Connected Grain Boundaries

is included in this parameter. Now we can calculate ﬁrst the term e(D)for

this grain as follows:

e(D)=



=6d +12a (4.112)

the term L(D) can also be easily calculated:

L(D)=

2π



2π



π · 6d +

π · 12a



+d+2a (4.113)

where L

is the unknown mean width of the two curved grain boundaries of

the grain. Because all other grain boundaries are ﬂat, β = 0 and their surfaces

do not contribute to the mean width.

From Eqs. (4.105), (4.112) and (4.113), we arrive at

= −2πm



+ d +2a − d − 2a



= −2m

γL

(4.114)

The volume change rate for the conﬁguration considered is determined by the

term L

which represents only the curved grain boundaries. It can be seen

that Eq. (4.114) delivers a constant rate dV/dt and complies with reality since

the conﬁguration in Fig. 4.61 demonstrates a steady-state evolution of its vol-

ume.

In order to compare the diﬀerent approaches the volume rate of change was

normalized by the cubic root of the volume of the grains at any time, and for

the case of the Cahn-MacPherson-Srolovitz approach Eq. (4.108) was used.

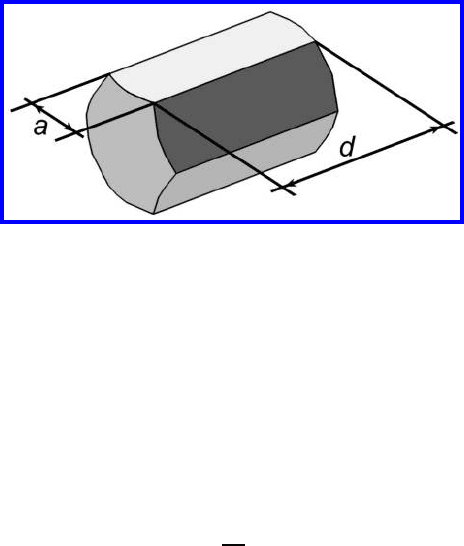
Fig. 4.62 shows the temporal evolution of the volume and the normalized

volume rate of change for a 3-sided grain (Fig. 4.60). The volume is seen to

decrease non-linearly with time (Fig. 4.62) indicating that, as predicted by

Eqs. (4.104) and (4.108), there is not a constant volume rate of change (

V )

for a particular topological class. Since the parameters in Eq. (4.104) change

with time,

V cannot have a constant value unless special conditions are met

as in the case of the hexagonal prism [542]. The normalized volume rate of

change (Fig. 4.62b) also does not seem to be constant with time. A compar-

ison of

−1/3

for the diﬀerent approaches evidences best agreement of the

simulations with the Cahn-MacPherson-Srolovitz approach Mullins’ model

(Eq. (4.99)) also yields reasonable agreement. This indicates that the expres-

sion

−1/3

of this particular grain is not far from the mean of the topological

class n = 3. The models of Hilgenfeldt et al. [545] and Glicksman-Rios [551]

cannot deliver a value for the topological class n = 3 since Eqs. (4.102) and

(4.103) become undetermined for this number of grain faces.

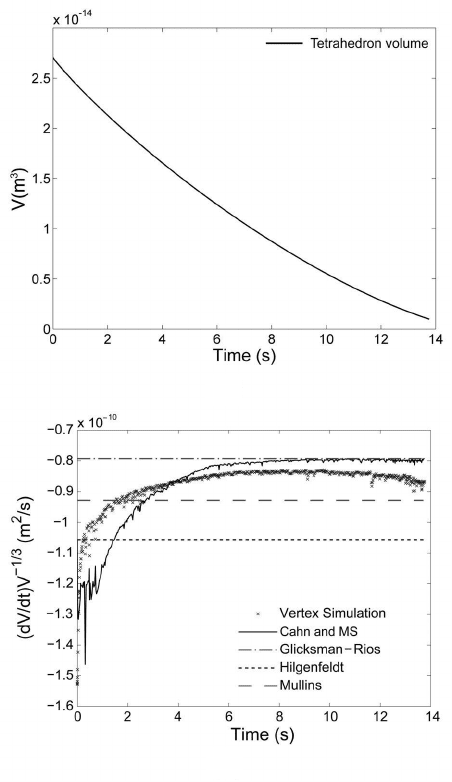
The evolution of the tetrahedral grain shows similar features, a non-linear

dependency of the volume on time (Fig. 4.64) and, consequently, a non-

constant

V ; however,

−1/3

is closer to a constant value (Fig. 4.64b). As

in the previous case, the agreement with Eq. (4.108) is good. The observed

4.7 Grain Growth in 3D Systems 419

(a)

(b)

(a)

(b)

(a)

(b)

FIGURE 4.62

Volume evolution with time (a) and comparison of the volume rate of change

of a 3-sided grain with the diﬀerent model as calculated from the simulation

data. (b) The Hilgenfeldt and Glicksman-Rios models do not appear because

the volume rate of change of a grain with a topological class n = 3 cannot be

calculated with their approaches (Eqs. (4.102) and (4.103) become undeter-

mined [554]).

420 4 Thermodynamics and Kinetics of Connected Grain Boundaries

FIGURE 4.63

Reuleaux tetrahedron.

deviations in the beginning of the simulation are caused by the fact that the

starting conﬁgurations have ﬂat grain boundaries and thus need a certain re-

laxation time to attain the necessary curvature and equilibrium at the triple

lines. The tetrahedral grain is of special interest for the Glicksman-Rios model

[551]; the point is that the tetrahedral grain has a particular geometry, since

it resembles a Reuleaux tetrahedron that is formed by the intersection of four

spheres of equal radius with centers located at the surfaces of the neighboring

spheres (three-dimensional equivalent of the Reuleaux triangle (Fig. 4.63)).

This geometry is optimal to study the Glicksman-Rios approach [551] be-

cause during its evolution it meets the condition of a constant vertex-to-vertex

distance λ

that is assumed in this model, and thus Eq. (4.103) represents an

exact solution for the growth rate of this grain. The simulation results show, in

fact, excellent agreement with this model. The Hilgenfeld and Mullins models

[545] also show reasonable agreement.

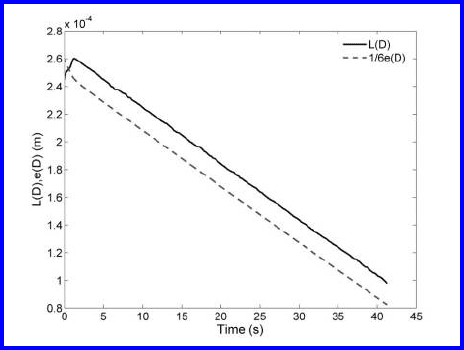
As shown in [542] the evolution of a hexagonal prism takes place in the

steady-state regime and

V = const. Fig. 4.65 shows the calculated parameters

L(D)ande(D) taken directly from the geometry of the evolving grain [542].

For a grain which evolves in a steady-state regime (

V = const) the curves

L(D, t)ande(D, t) need to be parallel (Eq. (4.104). One can see that this

condition is evidently fulﬁlled (Fig. 4.65).

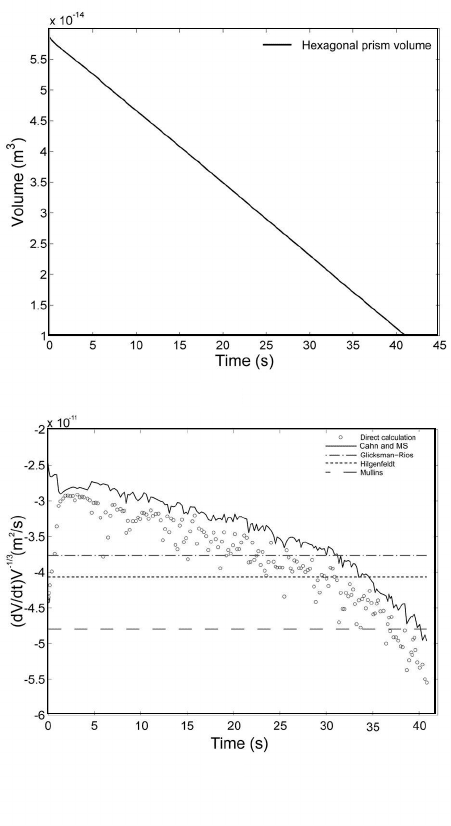
The results for the hexagonal prism (Fig. 4.66) show that the Cahn-

MacPherson–Srolovitz approach [552] is the only one that reproduces almost

exactly the evolution of the mean volume rate of change of the prism whereas

other approaches deviate from the simulation results since they can only ren-

der a constant value, yet, on average with reasonable agreement. It is also

conﬁrmed that neither a constant

V nor a constant

−1/3

can be expected

for a given topological class because of the dependency of the growth rate

on the metrics of the grain. For the 3-sided and tetragonal grain a constant

4.7 Grain Growth in 3D Systems 421

(a)

(b)

(a)

(b)

FIGURE 4.64

Volume evolution with time (a) and comparison of the volume rate of change of

a tetrahedral grain using the diﬀerent models as calculated from the simulation

data (b) [554].

422 4 Thermodynamics and Kinetics of Connected Grain Boundaries

FIGURE 4.65

The temporal evolution of the parameters L(D)ande(D) for a hexagonal

prism [554].

V cannot be achieved. It is be stressed that even in these cases a constant

−1/3

is highly debatable since any perturbation in the geometry of the

grains from the assumed ones will lead to deviations from the expected val-

ues. The hexagonal prism shrinks at constant

V and, therefore, cannot deliver

a constant

−1/3

The analysis of the data of Fig. 4.66b reveals another interesting feature.

The deviation between the Cahn-MacPherson-Srolovitz relation and the nor-

malized volume rate of change remains constant for the entire simulation (with

the exception of the incipient relaxation time). This occurs because the area

of the grain boundaries that provides the driving force for the reduction of

the volume of the grain does not change and, accordingly, the surface is rep-

resented by about the same quantity of triangular facets. Thus, the numerical

error remains constant. The reduction of the grain boundary area and, hence,

of the free energy, occurs at the expense of the lateral ﬂat grain boundaries

of the grain.

The results presented demonstrated that the Cahn-MacPherson-Srolovitz

relation 4.104 delivers the best description for the curvature-driven grain vol-

ume change under speciﬁc controlled conditions. Despite the simplicity of the

conﬁgurations studied, the results indicate that a grain of a given topological

class can only shrink or grow with a constant

−1/3

V under special

conditions. The volume rate of change of normal closed domains for constant

topological class will scatter over a certain range depending on the change

in the metrics of the grain L(D)ande(D) in Eq. (4.104) until a topological

transformation occurs that changes the topological class of the grain.

4.7 Grain Growth in 3D Systems 423

(a)

(b)

(a)

(b)

FIGURE 4.66

Volume evolution with time (a) and comparison of the volume rate of change

of a hexagonal prismatic grain predicted by diﬀerent models and simulation

data (b) [554].

424 4 Thermodynamics and Kinetics of Connected Grain Boundaries

FIGURE 4.67 (SEE COLOR INSERT FOLLOWING PAGE 424)

Polycrystal used in the simulation composed of 125 grains with periodic

boundary conditions [554].

4.7.2.2 3D Polycrystals

In the previous section we considered how the results of computer simula-

tions of the temporal evolution of the volume of solitary grains compare to

the diﬀerent analytical approaches [541, 542, 554]. However, the behavior of

a single grain is not the major goal of the approaches discussed. The main

objective is to ﬁnd a key to describe the grain growth in 3D polycrystal, to

compute the rate of change of the volume of the grains in complex grain as-

semblies. This problem was considered in [554], where the grain growth in

a polycrystal composed of 125 grains (Fig. 4.67) was studied quantitatively.

The volume rate of change of all grains showed very good agreement with

the Cahn-MacPherson-Srolovitz relation. In Fig. 4.68, an example of three

grains with diﬀerent growth rates is shown. During growth the grains suﬀer

topological changes by gaining and losing grain boundaries [554]. One can see

that the volume rate of change

V is apparently aﬀected less by the change

in the topological class than by the change in the metrics of the grains as

substantiated also by the good agreement of the Cahn-MacPherson-Srolovitz

relation with simulation results. In ([554]) it was shown that the evolution

of individual grains and grain growth in polycrystal are well described by

the Cahn-MacPherson-Srolovitz relation. An agreement between this relation