Готман В.И. Короткие замыкания и несимметричные режимы в электроэнергетических системах

Подождите немного. Документ загружается.

101

x Ɇɨɳɧɨɫɬɶ ɤɨɪɨɬɤɨɝɨ ɡɚɦɵɤɚɧɢɹ ɨɩɪɟɞɟɥɹɟɬɫɹ ɩɨ ɮɨɪɦɭɥɟ:



ɫɪ

SI U

, ɢɥɢ



SIS

. (5.15)

Ɍɚɛɥɢɰɚ 5.3

Ɂɧɚɱɟɧɢɹ

T ɞɥɹ ɧɚɢɛɨɥɟɟ ɱɚɫɬɨ ɜɫɬɪɟɱɚɸɳɢɯɫɹ ɷɥɟɦɟɧɬɨɜ ɗɗɋ

Ɇɟɫɬɨ ɤɨɪɨɬɤɨɝɨ ɡɚɦɵɤɚɧɢɹ ɢ ɯɚɪɚɤɬɟɪɢɫɬɢɤɚ

ɫɟɬɢ

, ɫ

1. ɋɛɨɪɧɵɟ ɲɢɧɵ 6–10 ɤȼ ɫɬɚɧɰɢɣ ɫ ɝɟɧɟɪɚɬɨɪɚɦɢ

ɦɨɳɧɨɫɬɶɸ 30–60 Ɇȼɬ

0,127–0,254 1,92–1,96

2. Ɂɚ ɥɢɧɟɣɧɵɦ ɪɟɚɤɬɨɪɨɦ ɞɨ 1000 Ⱥ,

ɩɪɢɫɨɟɞɢɧɟɧɧɵɦ ɤ ɫɛɨɪɧɵɦ ɲɢɧɚɦ, ɩɨ ɩ. 1

0,0634–0,191 1,85–1,95

3. ɋɛɨɪɧɵɟ ɲɢɧɵ ɩɨɜɵɲɟɧɧɨɝɨ ɧɚɩɪɹɠɟɧɢɹ ɫɬɚɧ-

ɰɢɣ ɫ ɬɪɚɧɫɮɨɪɦɚɬɨɪɚɦɢ ɦɨɳɧɨɫɬɶɸ 100 ɆȼȺ

ɢ ɜɵɲɟ

0,0955–0,191 1,89–1,95

4. Ɍɨ ɠɟ ɫ ɬɪɚɧɫɮɨɪɦɚɬɨɪɚɦɢ 30–100 ɆȼȺ 0,0634–0,159 1,85–1,94

5. ɋɛɨɪɧɵɟ ɲɢɧɵ ɜɬɨɪɢɱɧɨɝɨ ɧɚɩɪɹɠɟɧɢɹ

ɩɨɞɫɬɚɧɰɢɣ ɫ ɬɪɚɧɫɮɨɪɦɚɬɨɪɚɦɢ ɦɨɳɧɨɫɬɶɸ

100 ɆȼȺ ɢ ɜɵɲɟ; ɫɨɩɪɨɬɢɜɥɟɧɢɟ ɬɪɚɧɫɮɨɪɦɚɬɨ-

ɪɨɜ ɫɨɫɬɚɜɥɹɟɬ 90 % ɢ ɜɵɲɟ ɪɟɡɭɥɶɬɢɪɭɸɳɟɝɨ

ɫɨɩɪɨɬɢɜɥɟɧɢɹ ɞɨ ɦɟɫɬɚ ɄɁ

0,0634–0,127 1,85–1,92

6. Ɍɨ ɠɟ ɫ ɬɪɚɧɫɮɨɪɦɚɬɨɪɚɦɢ 30–100 ɆȼȺ 0,048–0,0955 1,81–1,89

7. Ɋɚɫɩɪɟɞɟɥɢɬɟɥɶɧɵɟ ɫɟɬɢ 6–10 ɤȼ 0,01 1,869

8. ȼɟɬɜɢ, ɡɚɳɢɳɚɟɦɵɟ ɪɟɚɤɬɨɪɨɦ ɫ ɧɨɦɢɧɚɥɶɧɵɦ

ɬɨɤɨɦ 630 Ⱥ ɢ ɧɢɠɟ

0,1 1,904

9. Ɍɭɪɛɨɝɟɧɟɪɚɬɨɪɵ ɦɨɳɧɨɫɬɶɸ:

100–1000 Ɇȼɬ;

12–60 Ɇȼɬ

0,4–0,54;

0,16–0,25

1,975–1,98;

1,94–1,955

10. Ȼɥɨɤɢ, ɫɨɫɬɨɹɳɢɟ ɢɡ ɬɭɪɛɨɝɟɧɟɪɚɬɨɪɚ ɢ ɩɨɜɵ-

ɲɚɸɳɟɝɨ ɬɪɚɧɫɮɨɪɦɚɬɨɪɚ, ɩɪɢ ɦɨɳɧɨɫɬɢ ɝɟɧɟɪɚ-

ɬɨɪɚ:

100–200 Ɇȼɬ;

300 Ɇȼɬ;

500 Ɇȼɬ;

800 Ɇȼɬ

0,26;

0,32;

0,35;

0,30

1,965;

1,977;

1,983;

1,967

11. ɋɢɫɬɟɦɚ, ɫɜɹɡɚɧɧɚɹ ɫ ɲɢɧɚɦɢ (ɝɞɟ ɪɚɫɫɦɚɬɪɢ-

ɜɚɟɬɫɹ ɄɁ) ɜɨɡɞɭɲɧɵɦɢ ɥɢɧɢɹɦɢ, ɧɚɩɪɹɠɟɧɢɟɦ:

35 ɤȼ;

110–150 ɤȼ;

220–330 ɤȼ;

500–750 ɤȼ

0,02;

0,02–0,03;

0,03–0,04;

0,06–0,08

1,608;

1,608–1,717;

1,717–1,78;

1,85–1,895

102

5.3. ɋɛɬɲɠɭ ɪɠɫɣɩɟɣɲɠɬɥɩɤ ɬɦɛɞɛɠɧɩɤ ɭɩɥɛ ɥɩɫɩɭɥɩɞɩ ɢɛɧɶɥɛɨɣɺ

ɝ ɪɫɩɣɢɝɩɦɷɨɶɤ ɧɩɧɠɨɭ ɝɫɠɧɠɨɣ

ɇɚ ɧɚɱɚɥɶɧɨɣ ɫɬɚɞɢɢ ɩɟɪɟɯɨɞɧɨɝɨ ɩɪɨɰɟɫɫɚ ɩɪɨɢɫɯɨɞɢɬ ɡɚɬɭɯɚɧɢɟ

ɩɟɪɢɨɞɢɱɟɫɤɢɯ ɫɥɚɝɚɟɦɵɯ ɬɨɤɚ ɄɁ, ɫɨɡɞɚɧɧɵɯ ɝɟɧɟɪɚɬɨɪɚɦɢ, ɫɢɧɯɪɨɧɧɵɦɢ

ɤɨɦɩɟɧɫɚɬɨɪɚɦɢ ɢ ɞɜɢɝɚɬɟɥɹɦɢ. ɋɤɨɪɨɫɬɶ ɷɬɨɝɨ ɡɚɬɭɯɚɧɢɹ ɫɭɳɟɫɬɜɟɧɧɨ ɡɚ-

ɜɢɫɢɬ ɨɬ ɬɢɩɚ ɢɫɬɨɱɧɢɤɚ ɢ ɟɝɨ ɷɥɟɤɬɪɢɱɟɫɤɨɣ ɭɞɚɥɟɧɧɨɫɬɢ ɞɨ ɦɟɫɬɚ ɄɁ. ɑɟɦ

ɛɥɢɠɟ ɢɫɬɨɱɧɢɤ, ɬɟɦ ɛɨɥɶɲɟ ɫɤɨɪɨɫɬɶ ɡɚɬɭɯɚɧɢɹ.

ȼ ɩɪɚɤɬɢɱɟɫɤɢɯ ɪɚɫɱɟɬɚɯ

ɭɱɟɬ ɮɚɤɬɨɪɚ ɜɪɟɦɟɧɢ ɢ ɭɞɚɥɟɧɧɨɫɬɢ ɢɫɬɨɱɧɢɤɚ ɧɚ ɩɟɪɢɨɞɢɱɟɫɤɭɸ ɫɥɚɝɚɟ-

ɦɭɸ ɨɫɭɳɟɫɬɜɥɹɟɬɫɹ ɩɨ ɪɚɫɱɟɬɧɵɦ ɤɪɢɜɵɦ. Ɉɧɢ ɩɨɫɬɪɨɟɧɵ ɞɥɹ ɪɚɡɥɢɱɧɵɯ

ɬɢɩɨɜ ɝɟɧɟɪɚɬɨɪɨɜ, ɫɢɧɯɪɨɧɧɵɯ ɢ ɚɫɢɧɯɪɨɧɧɵɯ ɞɜɢɝɚɬɟɥɟɣ.

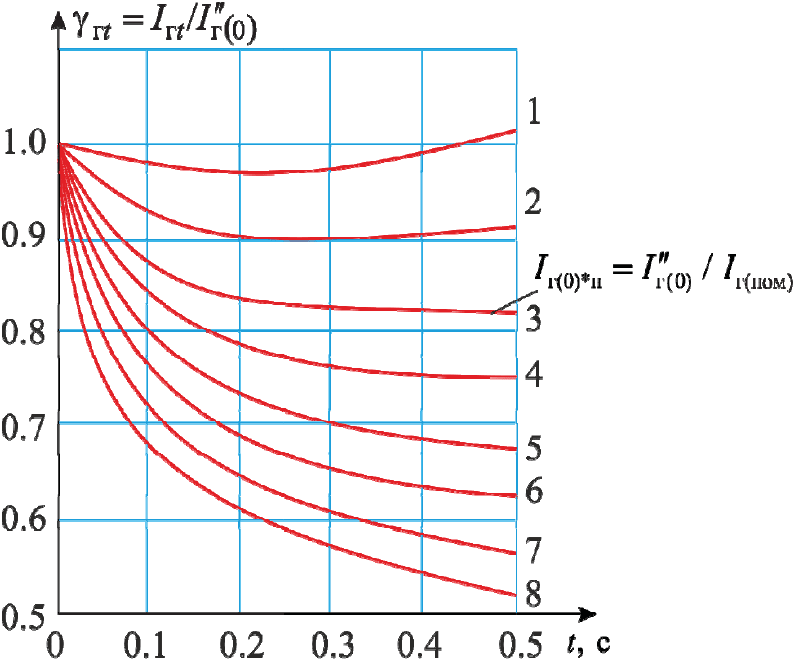
Ɋɚɫɱɟɬɧɵɟ ɤɪɢɜɵɟ ɞɥɹ ɝɟɧɟɪɚɬɨɪɨɜ ɩɪɟɞɫɬɚɜɥɹɸɬ ɝɪɚɮɢɱɟɫɤɨɟ

ɢɡɨɛɪɚɠɟɧɢɟ ɫɟɦɟɣɫɬɜɚ ɡɚɜɢɫɢɦɨɫɬɟɣ:



ɝ 0

, (5.16)

ɝɞɟ



ɝ 0

ɝ t

I – ɩɟɪɢɨɞɢɱɟɫɤɢɟ ɫɥɚɝɚɟɦɵɟ ɬɨɤɚ ɄɁ ɫɨɨɬɜɟɬɫɬɜɟɧɧɨ

ɞɥɹ ɦɨɦɟɧɬɚ

0t ɢ ɩɪɨɢɡɜɨɥɶɧɨɝɨ ɜɪɟɦɟɧɢ

Ɋɚɫɱɟɬɧɵɟ ɤɪɢɜɵɟ ɩɨɫɬɪɨɟɧɵ ɞɥɹ ɪɚɡɥɢɱɧɵɯ ɭɞɚɥɟɧɧɨɫɬɟɣ ɤɨɪɨɬ-

ɤɨɝɨ ɡɚɦɵɤɚɧɢɹ (ɫɦ. ɧɚ ɪɢɫ. 5.2 ɤɪɢɜɵɟ, ɨɛɨɡɧɚɱɟɧɧɵɟ ɰɢɮɪɚɦɢ ɨɬ 1 ɞɨ

8). ɉɨɥɨɠɟɧɢɟ ɪɚɫɱɟɬɧɵɯ ɤɪɢɜɵɯ ɨɩɪɟɞɟɥɹɟɬɫɹ ɩɚɪɚɦɟɬɪɨɦ



ɝ 0

ɝ 0*ɧɨɦ

ɧɨɦ

var

, (5.17)

ɝɞɟ



ɧɨɦ

– ɧɨɦɢɧɚɥɶɧɵɣ ɬɨɤ ɝɟɧɟɪɚɬɨɪɚ.

ɉɪɢ ɛɥɢɡɤɢɯ ɄɁ ɬɨɤ ɝɟɧɟɪɚɬɨɪɚ ɫɭɳɟɫɬɜɟɧɧɨ ɜɨɡɪɚɫɬɚɟɬ ɩɨ ɨɬɧɨ-

ɲɟɧɢɸ ɤ ɧɨɦɢɧɚɥɶɧɨɦɭ, ɬɚɤ ɱɬɨ ɩɚɪɚɦɟɬɪ



ɝ 0*ɧɨɦ

ɜɟɥɢɤ. ȿɝɨ ɦɚɤɫɢ-

ɦɚɥɶɧɨɦɭ ɡɧɚɱɟɧɢɸ ɫɨɨɬɜɟɬɫɬɜɭɟɬ ɤɨɪɨɬɤɨɟ ɡɚɦɵɤɚɧɢɟ ɧɚ ɲɢɧɚɯ ɝɟɧɟɪɚ-

ɬɨɪɚ. Ⱦɥɹ ɫɪɟɞɧɢɯ ɡɧɚɱɟɧɢɣ ɫɜɟɪɯɩɟɪɟɯɨɞɧɨɣ ɗȾɋ (

= 1,08) ɢ ɪɟɚɤɬɢɜ-

ɧɨɫɬɢ ɝɟɧɟɪɚɬɨɪɚ (

= 0,135) ɢɦɟɟɦ



ɝ 0*ɧɨɦ

1,08/0,135 = 8, ɱɬɨ

ɫɨɨɬɜɟɬɫɬɜɭɟɬ ɪɚɫɱɟɬɧɨɣ ɤɪɢɜɨɣ ɩɨɞ ɧɨɦɟɪɨɦ 8 ɧɚ ɪɢɫ. 5.2.

ɉɨ ɦɟɪɟ ɭɞɚɥɟɧɢɹ ɬɨɱɤɢ ɄɁ ɤɪɚɬɧɨɫɬɶ



Ƚ 0*ɧɨɦ

ɫɧɢɠɚɟɬɫɹ ɢ ɜ

ɩɪɟɞɟɥɟ ɫɬɪɟɦɢɬɫɹ ɤ 1. ɗɬɨ ɧɚɫɬɨɥɶɤɨ ɭɞɚɥɟɧɧɨɟ ɄɁ, ɱɬɨ ɧɚɩɪɹɠɟɧɢɟ ɧɚ

ɲɢɧɚɯ ɝɟɧɟɪɚɬɨɪɚ ɨɫɬɚɟɬɫɹ ɧɟɢɡɦɟɧɧɵɦ; ɬɨɤ ɤɨɪɨɬɤɨɝɨ ɡɚɦɵɤɚɧɢɹ ɪɚ-

ɜɟɧ ɟɝɨ ɧɨɦɢɧɚɥɶɧɨɦɭ ɬɨɤɭ.

Ɍɢɩɨɜɵɟ ɤɪɢɜɵɟ ɩɪɟɞɨɩɪɟɞɟɥɹɸɬ ɩɪɨɫɬɨɣ ɚɥɝɨɪɢɬɦ ɢɯ ɩɪɢɦɟɧɟɧɢɹ.

ɉɨ ɭɫɥɨɜɧɨɣ ɷɥɟɤɬɪɢɱɟɫɤɨɣ ɭɞɚɥɟɧɧɨɫɬɢ ɬɨɱɤɢ ɄɁ, ɯɚɪɚɤɬɟɪɢɡɭɟɦɨɣ

ɩɚɪɚɦɟɬɪɨɦ



ɝ 0*ɧɨɦ

, ɜɵɛɢɪɚɸɬ ɫɨɨɬɜɟɬɫɬɜɭɸɳɭɸ ɪɚɫɱɟɬɧɭɸ ɤɪɢɜɭɸ.

Ⱦɥɹ ɡɚɞɚɧɧɨɝɨ ɜɪɟɦɟɧɢ

ɤɚɥɢ ɞɨ ɩɟɪɟɫɟɱɟɧɢɹ ɫ ɜɵɛ

ɫɟɱɟɧɢɹ ɨɛɪɚɳɚɸɬɫɹ ɤ ɨɫ

ɷɮɮɢɰɢɟɧɬɚ ɡɚɬɭɯɚɧɢɹ ɬɨ

ɫɤɢɣ ɬɨɤ ɞɥɹ ɩɪɢɧɹɬɨɝɨ ɜɪ

ɉɪɢɜɟɞɟɧɧɵɟ ɧɚ ɪɢɫ

ɜɚɧɧɵɦɢ ɢ ɩɪɢɦɟɧɢɦɵ ɞɥ

ɝɢɞɪɨɝɟɧɟɪɚɬɨɪɨɜ ɦɨɳɧɨɫ

ɦɨɳɧɨɫɬɶɸ 37,5…100 Ɇ

ɬɢɥɶɧɨɣ ɫɢɫɬɟɦɨɣ ɜɨɡɛɭ

ɜɨɡɛɭɠɞɟɧɢɹ ɩɪɢ ɮɨɪɫɢɪɨ

Ɋɢɫ. 5.2. Ɋɚɫɱɟɬɧɵɟ ɤ

ɫɨɫɬɚɜɥɹɸɳɟɣ ɬɨɤɚ

ɭɞɚɥɟɧɧɨɫ

ɇɚ ɪɢɫ. 5.3–5.5 ɩɪɢ

ɚɫɢɧɯɪɨɧɧɵɯ ɞɜɢɝɚɬɟɥɟɣ.

103

ɚ ɨɫɢ ɚɛɫɰɢɫɫ ɩɨɞɧɢɦɚɸɬɫɹ ɜɜɟɪɯ

ɪɚɧɧɨɣ ɪɚɫɱɟɬɧɨɣ ɤɪɢɜɨɣ. ɋ ɷɬɨɣ ɬɨ

ɨɪɞɢɧɚɬ, ɧɚ ɤɨɬɨɪɨɣ ɩɨɥɭɱɚɸɬ ɡɧɚɱ

, ɱɬɨ ɩɨɡɜɨɥɹɟɬ ɪɚɫɫɱɢɬɚɬɶ ɩɟ

ɦɟɧɢ

ɩɨ ɜɵɪɚɠɟɧɢɸ

ɝɝɝ(0)tt

. 5.2 ɪɚɫɱɟɬɧɵɟ ɤɪɢɜɵɟ ɹɜɥɹɸɬɫɹ ɭɧɢ

ɬɭɪɛɨɝɟɧɟɪɚɬɨɪɨɜ ɦɨɳɧɨɫɬɶɸ 12…

ɶɸ ɞɨ 500 Ɇȼɬ ɢ ɫɢɧɯɪɨɧɧɵɯ ɤɨɦɩɟ

Ⱥ. ɗɬɢ ɤɪɢɜɵɟ ɩɨɫɬɪɨɟɧɵ ɞɥɹ ɦɚɲ

ɞɟɧɢɹ. ɇɚɪɚɫɬɚɧɢɟ ɧɚɩɪɹɠɟɧɢɹ ɧɚ

ɤɟ ɩɪɨɢɫɯɨɞɢɬ ɫɤɚɱɤɨɨɛɪɚɡɧɨ, ɬ. ɟ.

ɢɜɵɟ ɢɡɦɟɧɟɧɢɹ ɜɨ ɜɪɟɦɟɧɢ ɩɟɪɢɨɞɢɱɟɫ

Ɂ ɫɢɧɯɪɨɧɧɵɯ ɝɟɧɟɪɚɬɨɪɨɜ ɩɪɢ ɪɚɡɥɢɱɧ

ɹɯ ɬɨɱɤɢ ɤɨɪɨɬɤɨɝɨ ɡɚɦɵɤɚɧɢɹ

ɟɞɟɧɵ ɪɚɫɱɟɬɧɵɟ ɤɪɢɜɵɟ ɞɥɹ ɫɢɧɯɪ

ɨ ɜɟɪɬɢ-

ɤɢ ɩɟɪɟ-

ɟɧɢɟ

ɨ-

ɢɨɞɢɱɟ-

(5.18)

ɮɢɰɢɪɨ-

00 Ɇȼɬ,

ɫɚɬɨɪɨɜ

ɧ ɫ ɜɟɧ-

ɨɛɦɨɬɤɟ

ɨɣ

ɧɧɵɯ ɢ

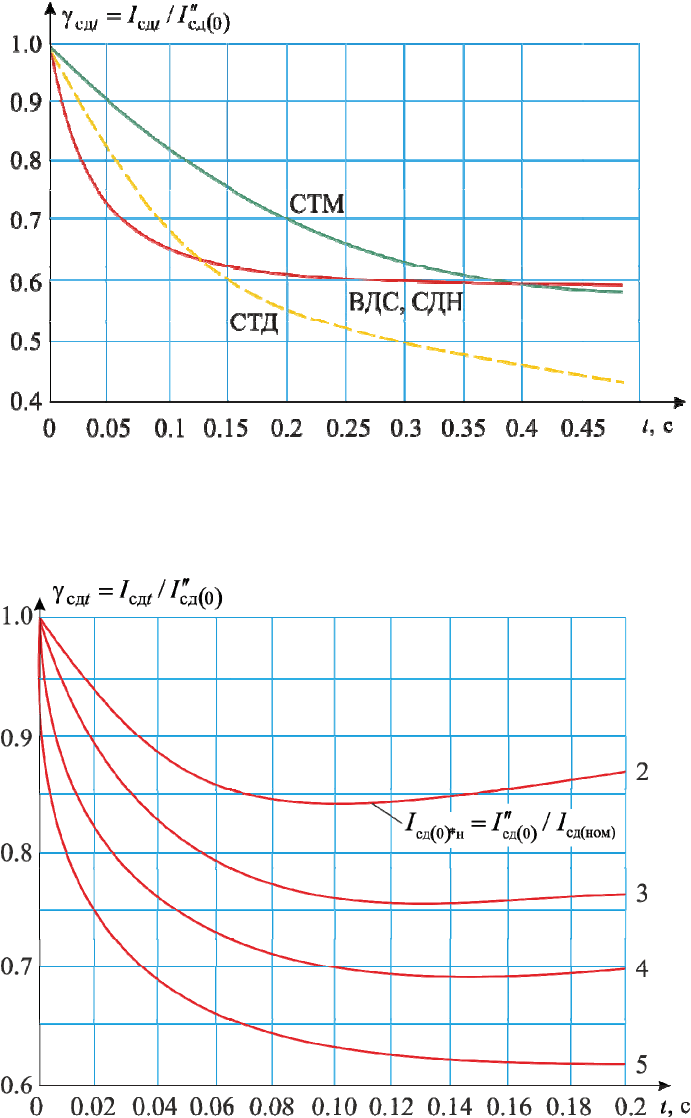
Ɋɢɫ. 5.3. Ɋɚɫɱɟɬɧɵɟ ɤ

ɫɨɫɬɚɜɥɹɸɳɟ

ɫɜɹɡɚɧɧɵ

Ɋɢɫ. 5.4. Ɋɚɫɱɟɬɧɵɟ ɤ

ɫɨɫɬɚɜɥɹɸɳɟɣ ɬɨɤɚ

ɭɞ

104

ɢɜɵɟ ɢɡɦɟɧɟɧɢɹ ɜɨ ɜɪɟɦɟɧɢ ɩɟɪɢɨɞɢɱɟɫ

ɬɨɤɚ Ʉ

ɫɢɧɯɪɨɧɧɵɯ ɞɜɢɝɚɬɟɥɟɣ,

ɧɟɩɨɫɪɟɞɫɬɜɟɧɧɨ ɫ ɬɨɱɤɨɣ ɄɁ

ɢɜɵɟ ɢɡɦɟɧɟɧɢɹ ɜɨ ɜɪɟɦɟɧɢ ɩɟɪɢɨɞɢɱɟɫ

ɫɢɧɯɪɨɧɧɵɯ ɞɜɢɝɚɬɟɥɟɣ ɩɪɢ ɢɯ ɪɚɡɥɢɱɧɵ

ɥɟɧɧɨɫɬɹɯ ɨɬ ɬɨɱɤɢ Ʉ

ɨɣ

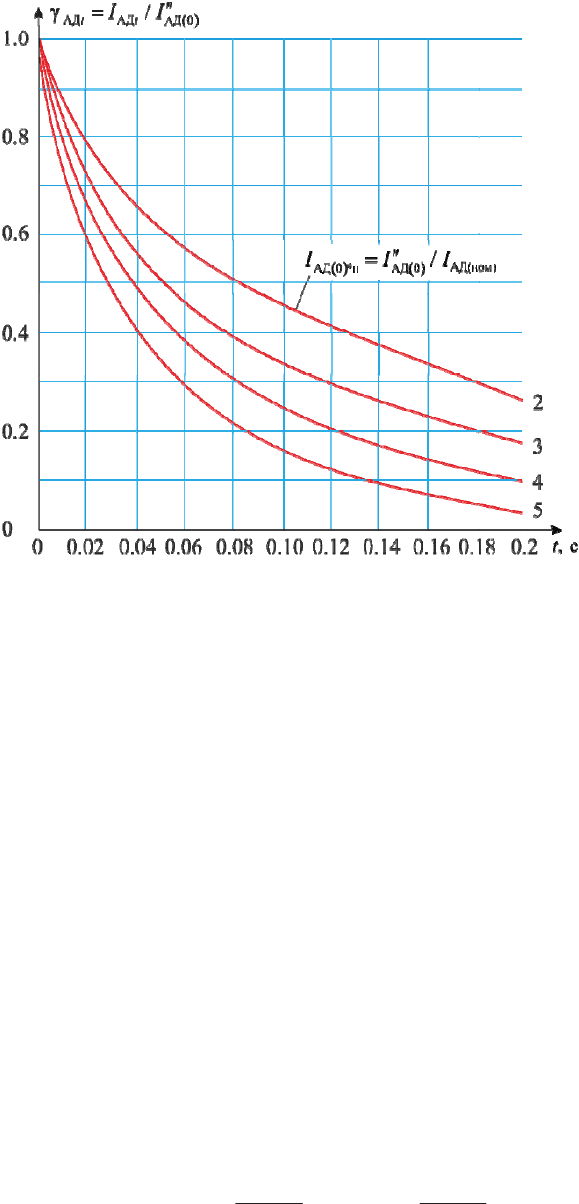
Ɋɢɫ. 5.5. Ɋɚɫɱɟɬɧɵɟ ɤ

ɫɨɫɬɚɜɥɹɸɳɟɣ ɬɨɤɚ

ɭɞɚ

ɉɪɢ ɪɚɫɱɟɬɟ ɩɟɪɢɨɞ

ɦɨɦɟɧɬ ɜɪɟɦɟɧɢ

ɜɫɟ ɷɬ

, ɨɫɬɚɸɬɫɹ ɜ ɫɢɥɟ. ɉ

ɞɢɜɢɞɭɚɥɶɧɵɣ ɭɱɟɬ ɢɫɬɨɱ

ɯɪɨɧɧɵɯ ɤɨɦɩɟɧɫɚɬɨɪɨɜ).

ɗɬɨɦɭ ɬɪɟɛɨɜɚɧɢɸ ɨ

Ⱦɥɹ ɢɫɬɨɱɧɢɤɨɜ ɩɢɬɚɧɢɹ,

ɟɡ ɨɛɳɢɟ ɜɟɬɜɢ, ɦɨɠɧɨ

ɩɪɟɞɟɥɟɧɢɹ ɫ.

Ⱦɥɹ ɝɟɧɟɪɚɬɨɪɨɜ, ɫɢ

ɥɹɟɬɫɹ ɩɚɪɚɦɟɬɪ ɢɯ ɷɥɟɤɬɪ

ɪɨɬɤɨɝɨ ɡɚɦɵɤɚɧɢɹ.

ɉɪɢ ɫɜɹɡɢ ɦɚɲɢɧɵ

ɧɨɫɬɶ ɷɬɨɬ ɩɚɪɚɦɟɬɪ ɪɚɫɫɱ



ɩ 0*

Ⱥ ɩɪɢ ɫɜɹɡɢ ɦɚɲɢɧ ɫ ɦɟɫɬ

ɜɵɪɚɠɟɧɢɸ:

105

ɢɜɵɟ ɢɡɦɟɧɟɧɢɹ ɜɨ ɜɪɟɦɟɧɢ ɩɟɪɢɨɞɢɱɟɫ

Ɂ ɚɫɢɧɯɪɨɧɧɵɯ ɞɜɢɝɚɬɟɥɟɣ ɩɪɢ ɪɚɡɥɢɱɧ

ɟɧɧɨɫɬɹɯ ɨɬ ɬɨɱɤɢ ɄɁ

ɱɟɫɤɨɣ ɫɥɚɝɚɟɦɨɣ ɬɨɤɚ ɄɁ ɜ ɩɪɨɢɡ

ɩɵ ɜɵɱɢɫɥɟɧɢɹ, ɢɡɥɨɠɟɧɧɵɟ ɜ ɪɚɡɞ.

ɢɦɟɧɟɧɢɟ ɬɢɩɨɜɵɯ ɤɪɢɜɵɯ ɩɪɟɞɩɨɥ

ɢɤɨɜ ɩɢɬɚɧɢɹ (ɝɟɧɟɪɚɬɨɪɨɜ, ɞɜɢɝɚɬɟ

ɬɜɟɱɚɟɬ ɥɭɱɟɜɚɹ ɫɯɟɦɚ ɨɬɧɨɫɢɬɟɥɶɧɨ

ɫɜɹɡɚɧɧɵɯ ɫ ɭɡɥɨɦ ɤɨɪɨɬɤɨɝɨ ɡɚɦɵɤ

ɜɨɫɩɨɥɶɡɨɜɚɬɶɫɹ ɤɨɷɮɮɢɰɢɟɧɬɚɦɢ

ɯɪɨɧɧɵɯ ɢ ɚɫɢɧɯɪɨɧɧɵɯ ɞɜɢɝɚɬɟɥɟɣ

ɢɱɟɫɤɨɣ ɭɞɚɥɟɧɧɨɫɬɢ (



ɩ 0*ɧɨɦi

) ɞɨ

ɦɟɫɬɨɦ ɄɁ ɱɟɪɟɡ ɢɧɞɢɜɢɞɭɚɥɶɧɭɸ

ɬɵɜɚɟɬɫɹ ɩɨ ɮɨɪɦɭɥɟ:



ɩ 0

ɨɦ ɩ 0*ɛ

ɧɨɦ ɧɨɦ

ɦ ɄɁ ɱɟɪɟɡ ɨɛɳɢɟ ɞɥɹ ɧɢɯ ɪɟɚɤɬɢɜɧ

ɨɣ

ɨɥɶɧɵɣ

5.2 ɞɥɹ

ɝɚɟɬ ɢɧ-

ɟɣ, ɫɢɧ-

ɭɡɥɚ ɄɁ.

ɧɢɹ ɱɟ-

ɨɤɨɪɚɫ-

ɨɩɪɟɞɟ-

ɡɥɚ ɤɨ-

ɟɚɤɬɢɜ-

(5.19)

ɫɬɢ – ɩɨ

106

 

ɩ 0*ɧɨɦ ɩ 0*ɛ

ɧɨɦ

IIɫ

, (5.20)

ɝɞɟ



ɩ 0*ɛ

– ɫɭɦɦɚɪɧɨɟ ɡɧɚɱɟɧɢɟ ɩɟɪɢɨɞɢɱɟɫɤɨɝɨ ɬɨɤɚ ɤɨɪɨɬɤɨɝɨ ɡɚ-

ɦɵɤɚɧɢɹ ɨɬ ɝɪɭɩɩɵ ɢɫɬɨɱɧɢɤɨɜ ɩɪɢ

0t ɜ ɨɬɧɨɫɢɬɟɥɶɧɵɯ ɛɚɡɢɫɧɵɯ

ɟɞɢɧɢɰɚɯ; ɤɨɷɮɮɢɰɢɟɧɬ

1c ɫɨɨɬɜɟɬɫɬɜɭɟɬ ɜɟɬɜɢ ɫ ɬɨɤɨɦ



ɩ 0*ɛ

;

ɫ –

ɤɨɷɮɮɢɰɢɟɧɬ ɬɨɤɨɪɚɫɩɪɟɞɟɥɟɧɢɹ i-ɝɨ ɢɫɬɨɱɧɢɤɚ.

ɉɨ ɫɨɨɬɜɟɬɫɬɜɭɸɳɢɦ ɪɚɫɱɟɬɧɵɦ ɤɪɢɜɵɦ ɞɥɹ ɧɚɣɞɟɧɧɨɝɨ



ɩ 0*ɧɨɦi

ɢ ɡɚɞɚɧɧɨɝɨ ɜɪɟɦɟɧɢ

ɨɩɪɟɞɟɥɹɟɬɫɹ ɤɨɷɮɮɢɰɢɟɧɬ ɡɚɬɭɯɚɧɢɹ

ɩɟɪɢɨɞɢɱɟɫɤɨɝɨ ɬɨɤɚ. ɉɪɢ



ɩ 0*ɧɨɦ

I 

ɢɫɬɨɱɧɢɤ ɫɱɢɬɚɟɬɫɹ ɷɥɟɤ-

ɬɪɢɱɟɫɤɢ ɭɞɚɥɟɧɧɵɦ, ɚ ɩɟɪɢɨɞɢɱɟɫɤɚɹ ɫɥɚɝɚɟɦɚɹ ɧɟɢɡɦɟɧɧɨɣ ɜɨ ɜɪɟɦɟ-

ɧɢ, ɬ. ɟ.

. Ⱦɥɹ «ɫɢɫɬɟɦɵ», ɯɚɪɚɤɬɟɪɢɡɭɟɦɨɣ

constU , ɩɟɪɢɨɞɢ-

ɱɟɫɤɚɹ ɫɥɚɝɚɟɦɚɹ ɜɨ ɜɪɟɦɟɧɢ ɧɟɢɡɦɟɧɧɚ (

ɂɫɤɨɦɨɟ ɡɧɚɱɟɧɢɟ ɩɟɪɢɨɞɢɱɟɫɤɨɣ ɫɨɫɬɚɜɥɹɸɳɟɣ ɬɨɤɚ ɤɨɪɨɬɤɨɝɨ

ɡɚɦɵɤɚɧɢɹ ɜ ɡɚɞɚɧɧɵɣ ɦɨɦɟɧɬ ɜɪɟɦɟɧɢ ɨɩɪɟɞɟɥɹɟɬɫɹ ɩɨ ɜɵɪɚɠɟɧɢɸ:

 

ɩ 0 ɩ 0

ti jj

IIIc

cc cc



¦¦

. (5.21)

ɉɟɪɜɚɹ 6 ɨɬɧɨɫɢɬɫɹ ɤ ɢɫɬɨɱɧɢɤɚɦ, ɫɜɹɡɚɧɧɵɦ ɫ ɦɟɫɬɨɦ ɄɁ ɱɟɪɟɡ

ɢɧɞɢɜɢɞɭɚɥɶɧɵɟ ɜɟɬɜɢ; ɤɨɷɮɮɢɰɢɟɧɬɵ ɬɨɤɨɪɚɫɩɪɟɞɟɥɟɧɢɹ ɞɥɹ ɷɬɨɣ

ɝɪɭɩɩɵ ɢɫɬɨɱɧɢɤɨɜ ɧɟ ɪɚɫɫɱɢɬɵɜɚɸɬɫɹ. ȼɬɨɪɨɟ ɫɥɚɝɚɟɦɨɟ ɭɱɢɬɵɜɚɟɬ

ɝɪɭɩɩɭ ɢɫɬɨɱɧɢɤɨɜ, ɫɜɹɡɚɧɧɵɯ ɫ ɬɨɱɤɨɣ ɄɁ ɱɟɪɟɡ ɨɛɳɢɟ ɞɥɹ ɧɢɯ ɜɟɬɜɢ.

ɉɚɪɚɦɟɬɪ

ɩ (0)

ɹɜɥɹɟɬɫɹ ɪɟɡɭɥɶɬɢɪɭɸɳɢɦ ɬɨɤɨɦ ɷɬɨɣ ɝɪɭɩɩɵ ɢɫɬɨɱ-

ɧɢɤɨɜ; ɩɪɢ ɷɬɨɦ

ɞɨɥɠɧɚ ɛɵɬɶ ɪɚɜɧɚ ɟɞɢɧɢɰɟ. ȼ ɱɚɫɬɧɨɦ ɫɥɭɱɚɟ

ɨɞɧɚ ɢɡ ɫɭɦɦ ɜ ɜɵɪɚɠɟɧɢɢ (5.21) ɦɨɠɟɬ ɨɬɫɭɬɫɬɜɨɜɚɬɶ.

ɉɪɢɦɟɪ 5.1. Ⱦɥɹ ɩɪɢɧɰɢɩɢɚɥɶɧɨɣ ɫɯɟɦɵ ɩɨɞɫɬɚɧɰɢɢ, ɩɪɢɜɟɞɟɧ-

ɧɨɣ ɧɚ ɪɢɫ. 5.6, ɚ, ɩɪɢ ɬɪɟɯɮɚɡɧɨɦ ɄɁ ɜ ɬɨɱɤɟ K ɨɩɪɟɞɟɥɢɬɶ:

– ɫɭɦɦɚɪɧɭɸ ɩɟɪɢɨɞɢɱɟɫɤɭɸ ɫɨɫɬɚɜɥɹɸɳɭɸ ɬɨɤɚ ɞɥɹ

0t ;

– ɭɞɚɪɧɵɣ ɬɨɤ;

– ɧɚɢɛɨɥɶɲɟɟ ɞɟɣɫɬɜɭɸɳɟɟ ɡɧɚɱɟɧɢɟ ɬɨɤɚ ɤɨɪɨɬɤɨɝɨ ɡɚɦɵɤɚɧɢɹ;

– ɩɟɪɢɨɞɢɱɟɫɤɢɣ ɬɨɤ ɞɥɹ ɜɪɟɦɟɧɢ

= 0,2 ɫ.

ɉɚɪɚɦɟɬɪɵ ɷɥɟɦɟɧɬɨɜ ɫɯɟɦɵ

ɋɢɫɬɟɦɚ:

U 158 ɤȼ,

ɤɡ

4000S ɆȼȺ.

Ɍɪɚɧɫɮɨɪɦɚɬɨɪ ɫ ɪɚɫɳɟɩɥɟɧɧɨɣ ɨɛɦɨɬɤɨɣ ɧɚ ɫɬɨɪɨɧɟ 6,3 ɤȼ;

ɧɨɦ

32S ɆȼȺ,

ȼɇ

158 6,3UU ɤȼ,

(ȼ-ɇ )

12%

;

3,5K

– ɤɨ-

ɷɮɮɢɰɢɟɧɬ ɪɚɫɳɟɩɥɟɧɢɹ.

Ʉɚɛɟɥɶɧɵɟ ɥɢɧɢɢ:

Ⱦɜɢɝɚɬɟɥɶɧɚɹ ɧɚɝɪɭ

ɨɛɟɢɯ ɫɟɤɰɢɹɯ ɲɢɧ ɨɞɢɧɚ

ȺȾ-1 ɫɟɪ

ɧɨɦ

, ɤȼɬ

ɧɨɦ

, Ⱥ

*ɩɭɫɤ

,ɨ. ɟ.

cos

0.8

Ɋɢɫ. 5.6. Ʉ ɩɪɢɦɟɪɭ 5.1:

Ɋɟɲɟɧɢɟ

ȼ ɪɚɫɫɦɚɬɪɢɜɚɟɦɵɯ

ɚɫɩɨɥɨɠɟɧɧɨɣ ɧɚ ɫɨɫɟɞ

ɦɨɠɧɨ ɩɪɟɧɟɛɪɟɱɶ. ɋ ɰɟɥ

ɚɫɱɟɬɨɜ ɨɰɟɧɢɦ ɜɤɥɚɞ ɷɬɢ

107

750L

ɦ;

0,066x

0,21r

ɤɚ ɫ ɪɚɛɨɱɢɦ ɧɚɩɪɹɠɟɧɢɟɦ

6,1U

ɨɜɚɹ ɢ ɢɦɟɟɬ ɩɚɪɚɦɟɬɪɵ:

ɢ ȺɌȾ ɋȾ-2 ɫɟɪɢɢ ɋȾɇ ɋȾ-3 ɫɟɪ

1600 32

180 36

5 6.

9 0.95 0.9

– ɩɪɢɧɰɢɩɢɚɥɶɧɚɹ ɫɯɟɦɚ; ɛ, ɜ – ɫɯɟɦɵ ɡɚɦɟ

ɭɫɥɨɜɢɹɯ ɜɥɢɹɧɢɟɦ ɞɜɢɝɚɬɟɥɶɧɨɣ

ɟɣ ɩɨ ɨɬɧɨɲɟɧɢɸ ɤ ɬɨɱɤɟ ɄɁ ɫɟɤɰ

ɸ ɩɨɞɬɜɟɪɠɞɟɧɢɹ ɷɬɨɝɨ ɦɵ ɧɚ ɩɟɪɜ

ɯ ɞɜɢɝɚɬɟɥɟɣ (Ɇ1–Ɇ3) ɜ ɨɛɳɢɣ ɬɨɤ Ʉ

ɦ/ɤɦ.

ɤȼ ɧɚ

ɢ ɋȾɇ

ɟɧɢɹ

ɚɝɪɭɡɤɢ,

ɢ ɲɢɧ,

ɦ ɷɬɚɩɟ

Ɂ.

108

1. Ɋɚɫɱɟɬ ɩɚɪɚɦɟɬɪɨɜ ɫɯɟɦɵ ɡɚɦɟɳɟɧɢɹ (ɪɢɫ. 5.6, ɛ, ɜ)

ɉɪɢɧɢɦɚɟɦ

32S ɆȼȺ,

6,3U ɤȼ,

ɛ1

158U ɤȼ; ɧɚɯɨɞɢɦ

ɛɚɡɢɫɧɵɣ ɬɨɤ:

2,94

36,3



ɤȺ.

Ɋɚɫɫɱɢɬɵɜɚɟɦ ɫɨɩɪɨɬɢɜɥɟɧɢɹ ɢ ɗȾɋ ɷɥɟɦɟɧɬɨɜ ɫɯɟɦɵ ɡɚɦɟɳɟɧɢɹ

ɜ ɨɬɧɨɫɢɬɟɥɶɧɵɯ ɟɞɢɧɢɰɚɯ ɩɪɢ ɩɪɢɧɹɬɵɯ ɛɚɡɢɫɧɵɯ ɭɫɥɨɜɢɹɯ:

x ɫɢɫɬɟɦɵ:

ɤɡ

0,008

4000

ɛ1

158

;

x ɬɪɚɧɫɮɨɪɦɚɬɨɪɚ:

(ȼ-ɇ)

ɧɨɦ

12 32

0,125 0,125 0,015

100 100 32

 

;

3* 4*

12 32

1,75 0,21

100 32

xx  

;

x ɤɚɛɟɥɶɧɵɯ ɥɢɧɢɣ:

0 ɛ

5* 6*

0,066 0,75 32

0,0133

6,3

xL S



 

;

5* 6*

0,0423RR ;

x ɚɫɢɧɯɪɨɧɧɵɯ ɞɜɢɝɚɬɟɥɟɣ ȺȾ-1:

7* 8*

*ɩɭɫɤ ɧɨɦ

112,94

6,163

5,3 0,09

 

;

ɧɨɦ

ɧɨɦ*

0,09

0,031

2,34

;

ɪ*

6,15

0,976

6,3

ɋɜɟɪɯɩɟɪɟɯɨɞɧɵɟ ɗȾɋ ɪɚɫɫɱɢɬɵɜɚɟɦ ɩɨ ɜɵɪɚɠɟɧɢɸ (4.60):

 

7* 8* ɪ*0 ɪ*0ɧɨɦ*7*

cos sin

0,976 0,89 0,976 0,456 0,031 6,163 0,905.

EE U U Ix

cc cc

 



ɋɢɧɯɪɨɧɧɵɟ ɞɜɢɝɚɬɟɥɢ ɋȾ-2, ɋȾ-3 ɡɚɦɟɧɹɟɦ ɨɞɧɢɦ ɷɤɜɢɜɚɥɟɧɬ-

ɧɵɦ. ɉɨ ɜɵɪɚɠɟɧɢɸ (4.55) ɧɚɯɨɞɢɦ ɫɭɦɦɚɪɧɵɣ ɩɭɫɤɨɜɨɣ ɬɨɤ ɜ ɢɦɟɧɨ-

ɜɚɧɧɵɯ ɟɞɢɧɢɰɚɯ:

ɩɭɫɤ

5 180 6,6 360 3276I

  

Ⱥ,

ɧɨɦ*

0,18 0,36

0,1837

2,94



109

ɢ ɪɟɚɤɬɚɧɫɵ:

9* 10*

ɩɭɫɤ

2,94

0,897

3,276

ɋɜɟɪɯɩɟɪɟɯɨɞɧɵɟ ɗȾɋ ɫɢɧɯɪɨɧɧɵɯ ɞɜɢɝɚɬɟɥɟɣ ɞɥɹ ɪɟɠɢɦɚ ɩɟɪɟ-

ɜɨɡɛɭɠɞɟɧɢɹ ɧɚɯɨɞɢɦ ɩɨ ɜɵɪɚɠɟɧɢɸ (4.53):

 

9* 10*

0,976 0,95 0,976 0,31 0,1837 0,897 1,038EE

cc cc

    .

2. Ɋɚɫɱɟɬ ɩɚɪɚɦɟɬɪɨɜ ɬɨɤɚ ɄɁ ɞɥɹ t = 0 ɫ

ɗɤɜɢɜɚɥɟɧɬɧɵɟ ɩɚɪɚɦɟɬɪɵ ɫɯɟɦɵ ɩɟɪɜɨɣ ɫɟɤɰɢɢ ɲɢɧ ɨɬɧɨɫɢɬɟɥɶ-

ɧɨ ɬɨɱɤɢ ɄɁ:

11* 7* 9* 5*

// 0,796xxxx  ,

11 7* 9*

// 1,021EEE

cc cc cc

ɉɨɫɤɨɥɶɤɭ

5* 11

0,0423

Rx 

, ɬɨ ɢɦ ɦɨɠɧɨ ɩɪɟɧɟɛɪɟɱɶ.

ɗɤɜɢɜɚɥɟɧɬɧɵɟ ɩɚɪɚɦɟɬɪɵ ɨɬɧɨɫɢɬɟɥɶɧɨ ɭɡɥɚ N ɜɬɨɪɨɣ ɫɟɤɰɢɢ ɲɢɧ:

12* 8* 10*

// 1,021EEE

cc cc cc

12* 8* 10* 6* 4*

// 1,006xxxxx 

ɢ ɩɢɬɚɸɳɟɣ ɫɢɫɬɟɦɵ:

13* 1* 2*

0,023xxx  .

ɇɚɱɚɥɶɧɨɟ ɡɧɚɱɟɧɢɟ ɩɟɪɢɨɞɢɱɟɫɤɨɣ ɫɨɫɬɚɜɥɹɸɳɟɣ ɬɨɤɚ ɄɁ, ɫɨɡɞɚ-

ɜɚɟɦɨɝɨ ɢɫɬɨɱɧɢɤɚɦɢ

E ɢ

, ɫɨɫɬɚɜɥɹɟɬ



13*

0 ɫ+ɞɜ

14*

2,94

12,645

0,2325

ɤȺ,

ɝɞɟ

13* 12* 1

// 1,0EEE



cc cc

;

14* 12* 13* 3*

/ / 0,2325xxxx  .

ɉɪɟɧɟɛɪɟɝɚɹ ɜɥɢɹɧɢɟɦ ɞɜɢɝɚɬɟɥɶɧɨɣ ɧɚɝɪɭɡɤɢ Ɇ1–Ɇ3, ɧɚɯɨɞɢɦ

ɡɧɚɱɟɧɢɟ ɩɟɪɢɨɞɢɱɟɫɤɨɣ ɫɨɫɬɚɜɥɹɸɳɟɣ ɬɨɤɚ, ɝɟɧɟɪɢɪɭɟɦɨɝɨ ɬɨɥɶɤɨ

ɫɢɫɬɟɦɨɣ:



0 ɫ

13* 3*

2,94

12,62

0,023 0,21





ɤȺ,

ɱɬɨ ɞɚɟɬ ɩɨɝɪɟɲɧɨɫɬɶ 0,2 %.

ɉɟɪɢɨɞɢɱɟɫɤɢɣ ɬɨɤ ɄɁ, ɨɛɭɫɥɨɜɥɟɧɧɵɣ ɞɜɢɝɚɬɟɥɹɦɢ ɩɟɪɜɨɣ ɫɟɤ-

ɰɢɢ ɲɢɧ, ɜ ɨɬɧɨɫɢɬɟɥɶɧɵɯ ɢ ɢɦɟɧɨɜɚɧɧɵɯ ɟɞɢɧɢɰɚɯ:



0 ɞɜ*

11*

1, 0 2 1

1,282

0,796



0 ɞɜ

1, 28 2 2, 9 4 3, 77I



ɤȺ.

Ⱦɥɹ ɨɩɪɟɞɟɥɟɧɢɹ ɩɟɪɫɨɧɚɥɶɧɨɝɨ ɜɤɥɚɞɚ ɚɫɢɧɯɪɨɧɧɨɝɨ ɢ ɷɤɜɢɜɚ-

ɥɟɧɬɧɨɝɨ ɫɢɧɯɪɨɧɧɨɝɨ ɞɜɢɝɚɬɟɥɟɣ ɜ ɢɯ ɪɟɡɭɥɶɬɢɪɭɸɳɢɣ ɬɨɤ



0 ɞɜ

ɪɚɫ-

ɫɱɢɬɚɟɦ ɤɨɷɮɮɢɰɢɟɧɬɵ ɬɨɤɨɪɚɫɩɪɟɞɟɥɟɧɢɹ:

110



57* 9* 7*

0 ɞɜ*

7* 9*

1 6,163 1,038 0,905 /1,282

0,887

6,163 0,897

ɫ xEEI

cc cc cc



 



;

759

1 0,887 0,113ɫɫɫ   .

ɋɥɟɞɨɜɚɬɟɥɶɧɨ, ɧɚɱɚɥɶɧɵɣ ɩɟɪɢɨɞɢɱɟɫɤɢɣ ɬɨɤ ɜ ɦɟɫɬɟ ɄɁ ɩɟɪɫɨ-

ɧɚɥɶɧɨ ɨɬ ɤɚɠɞɨɝɨ ɢɡ ɞɜɢɝɚɬɟɥɟɣ ɫɨɫɬɚɜɥɹɟɬ:



0 ɚɞ

3,77 0,113 0,426I



ɤȺ,



0 ɞɫ

3,77 0,887 3,344I



ɤȺ,

ɢ ɪɟɡɭɥɶɬɢɪɭɸɳɢɣ ɬɨɤ, ɫɨɡɞɚɜɚɟɦɵɣ ɜɫɟɦɢ ɢɫɬɨɱɧɢɤɚɦɢ,

   

00C0ɚɞ 0 ɫɞ

12,62 0,426 3,344 16,39III I

cc cc cc cc

   

ɤȺ.

ɍɞɚɪɧɵɣ ɬɨɤ ɨɩɪɟɞɟɥɢɦ ɫ ɭɱɟɬɨɦ ɩɟɪɫɨɧɚɥɶɧɵɯ ɭɞɚɪɧɵɯ ɤɨɷɮɮɢ-

ɰɢɟɧɬɨɜ ɞɥɹ ɤɚɠɞɨɝɨ ɢɡ ɜɵɞɟɥɟɧɧɵɯ ɢɫɬɨɱɧɢɤɨɜ ɩɢɬɚɧɢɹ:

ɞɥɹ ɫɢɫɬɟɦɵ ɩɨ ɬɚɛɥ. 5.3, ɩ. 6 ɢɦɟɟɦ

ɭ(ɫ)

1,8 9K

;

ɞɥɹ ȺȾ ɫɟɪɢɢ ȺɌȾ ɩɨ ɬɚɛɥ. 4.4 ɢɦɟɟɦ

ɭ(ɚɞ)

1, 6 9K

;

ɞɥɹ ɋȾ ɫɟɪɢɢ ɋȾɇ ɩɨ ɬɚɛɥ. 4.3 ɢɦɟɟɦ

ɭ(ɫɞ)

1,8 9K

ɢ, ɫɥɟɞɨɜɚɬɟɥɶɧɨ,

  







ɭɭ(ɫ) ɭ(ɚɞ) ɭ(ɫɞ)

0 ɫ 0 ɚɞ 0 ɫɞ

2 12,62 1,89 0,426 1,69 3,344 1,89 43,68 ɤȺ.

iIKIKIK

cc cc cc





ɍɱɢɬɵɜɚɹ, ɱɬɨ ȺȾ ɞɚɟɬ ɧɟɡɧɚɱɢɬɟɥɶɧɵɣ ɜɤɥɚɞ ɜ

, ɩɨɫɥɟɞɧɢɣ

ɦɨɠɧɨ ɪɚɫɫɱɢɬɚɬɶ ɩɨ ɟɞɢɧɨɦɭ

ɭ(ɫ )

, ɩɪɢɧɹɬɨɦɭ ɞɥɹ ɫɢɫɬɟɦɵ:



ɭɭ(ɫ)

2216,391,8943,8iIK



ɤȺ (ɩɨɝɪɟɲɧɨɫɬɶ 0,3 %).

ɋ ɭɱɟɬɨɦ ɫɤɚɡɚɧɧɨɝɨ ɜɵɲɟ, ɧɚɯɨɞɢɦ ɧɚɢɛɨɥɶɲɟɟ ɞɟɣɫɬɜɭɸɳɟɟ

ɡɧɚɱɟɧɢɟ ɩɨɥɧɨɝɨ ɬɨɤɚ ɄɁ



ɭɭ(ɫ)

1 2 1 16,39 1 2 1,89 1 26,35II K

  

ɤȺ.

3. Ɋɚɫɱɟɬ ɩɟɪɢɨɞɢɱɟɫɤɨɝɨ ɬɨɤɚ ɞɥɹ ɜɪɟɦɟɧɢ

= 0,2 ɫ

ɉɟɪɢɨɞɢɱɟɫɤɚɹ ɫɥɚɝɚɟɦɚɹ ɬɨɤɚ ɨɬ ɫɢɫɬɟɦɵ ɜɨ ɜɪɟɦɟɧɢ ɧɟ ɢɡɦɟɧɹ-

ɟɬɫɹ, ɬ. ɟ.



12,62II

ɤȺ.

ɉɟɪɢɨɞɢɱɟɫɤɢɟ ɫɥɚɝɚɟɦɵɟ ɬɨɤɚ ȺȾ ɢ ɋȾ ɫɨ ɜɪɟɦɟɧɟɦ ɡɚɬɭɯɚɸɬ ɢ

ɨɩɪɟɞɟɥɹɸɬɫɹ ɩɨ ɫɨɨɬɜɟɬɫɬɜɭɸɳɢɦ ɬɢɩɨɜɵɦ ɤɪɢɜɵɦ.

Ɋɚɫɫɱɢɬɚɟɦ ɩɚɪɚɦɟɬɪ



ɩ 0*ɧɨɦ

ɞɥɹ ȺȾ:



0 ɚɞ

ɩ 0*ɧɨɦ

ɧɨɦ

0,426

4,73

0,09