Горкунова Т.В., Коробейникова Е.В. Учебно-практическое пособие по математике
Подождите немного. Документ загружается.


IV тип. Арифметические операции в различных системах счисления
Задача. Выполнить действие в 4-ой системе счисления: 13023
4
+ 3323
4
.
Решение.
Воспользуемся правилом сложения чисел в
q-ичной системе счисления.
То есть запишем второе слагаемое под первым, так чтобы разряды чисел
находились друг под другом:
Сложим цифры первого разряда справа по правилам 10-ой системы: 3+3 =
6, т. е. имеем случай, когда сумма больше основания системы счисления (4).
Представим 6 в 4-ой с. с.: 6
10
= 1 • 4 + 2 = 12
4
. Таким образом, в первый разряд
ответа запишем 2, а 1 перенесем в следующий разряд (2 пишем, 1 в уме).
Сложим цифры второго разряда справа по правилам 10-ой системы:
2 + 2 + 1 = 5. Сумма больше основания системы счисления (4). Представим 5 в
4-ой с. с.: 5
10
= 1 • 4 + 1 = 11
4
. Таким образом, во второй разряд ответа запишем
1, а 1 перенесем в следующий разряд (1 пишем, 1 в уме).
Сложим цифры третьего разряда справа по правилам 10-ой системы:
0 + 3 + 1 = 4. Сумма равна основанию системы счисления (4). Представим 4 в 4-
ой с. с.: 4
10
= 1 • 4 + 0 = 10
4
. Таким образом, в третий разряд ответа запишем 0, а
1 перенесем в следующий разряд (0 пишем, 1 в уме).
13023
4
13323
4
12
4
1
13023
4
13323
4
2
4
13023
4
13323
4
1
13023
4
13323
4
012
4
1
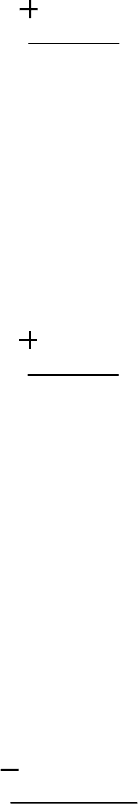
Сложим цифры четвертого разряда справа по правилам 10-ой системы:
1 + 3 + 3 = 7. Сумма больше основания системы счисления (4). Представим 7 в
4-ой с. с.: 7
10
= 1 • 4 + 3 = 13
4
. Таким образом, в четвертый разряд ответа
запишем 3, а 1 перенесем в следующий разряд (3 пишем, 1 в уме).
Сложим цифры пятого разряда справа по правилам 10-ой системы:
1 + 1 + 1 = 3. Сумма меньше основания системы счисления (4). Таким образом,
в пятый разряд ответа запишем 3, а в следующий разряд переносить ничего не
нужно.
Ответ: 33012
4
Задача. Выполнить действие в 6-ой системе счисления:
530002
6
– 42455
6
Решение.
Запишем вычитаемое под уменьшаемым так, чтобы соответствующие
разряды находились друг под другом:
Цифра вычитаемого в первом разряде меньше соответствующей цифры
уменьшаемого, цифры следующих четырех разрядов равны нулю, поэтому
цифру 3 из пятого (справа) разряда уменьшаемого уменьшим на единицу
(«займем единицу»), а нули увеличим до
q-1, т. е. до 5 (6-1). В первом разряде
уменьшаемого к 2 добавим
q = 6 и из полученных восьми отнимем 5 получим 3
– первую (с конца) цифру результата. по правилам 10-ой с.с.:
13023
4
13323
4
3012
4
1
13023
4
13323
4
33012
4
530002
6
42455
6

Точки будут напоминать о том, что из 3 произвели заем одной единицы, а
нули заменили 5. Цифра, стоящая во втором разряде уменьшаемого стала 5, 5 –
5 = 0. Цифра, стоящая в третьем разряде уменьшаемого стала 5, 5 – 4 = 1.
Цифра, стоящая в четвертом разряде уменьшаемого стала 5, 5 – 2 = 3.
В пятом разряде уменьшаемого вместо цифры 3 уже 2, в пятом разряде
вычитаемого 4. 2 < 4, следовательно, из шестого разряда
уменьшаемого займем
единицу (5-1 = 4), а в пятом разряде уменьшаемого к 2 добавляем
q = 6,
получим 8, и теперь из 8 вычтем 4, получим 4.
Точка над 5 означает, что из нее заняли единицу, теперь в шестом разряде
уменьшаемого стоит 4. В шестом разряде вычитаемого ничего нет, что
подразумевает 0. Итак, 4 – 0 = 4.
Ответ: 443103
6
.
Задача. Пользуясь сложением составить двоично-шестнадцатеричную
таблицу.
Решение.
530002
6
42455
6
443103
6
•
530002
6
42455
6
3103
6
• • • •
530002
6
42455
6
3
6
• • • •
530002
6
42455
6
43103
6
•

0
16
= 0
2
; 1
16
= 1
2
, 2 в шестнадцатиричной получается увеличением
единицы на 1. 2
16
= 1
16
+ 1
16
= 1
2
+ 1
2
= 2
10
= 1 • 2 + 0 = 10
2
. 3
16
= 2
16
+ 1
16
= 10
2
+
1
2
= 11
2
. Далее аналогично. Процесс сложения в двоичной системе счисления
представлен в таблице 13.
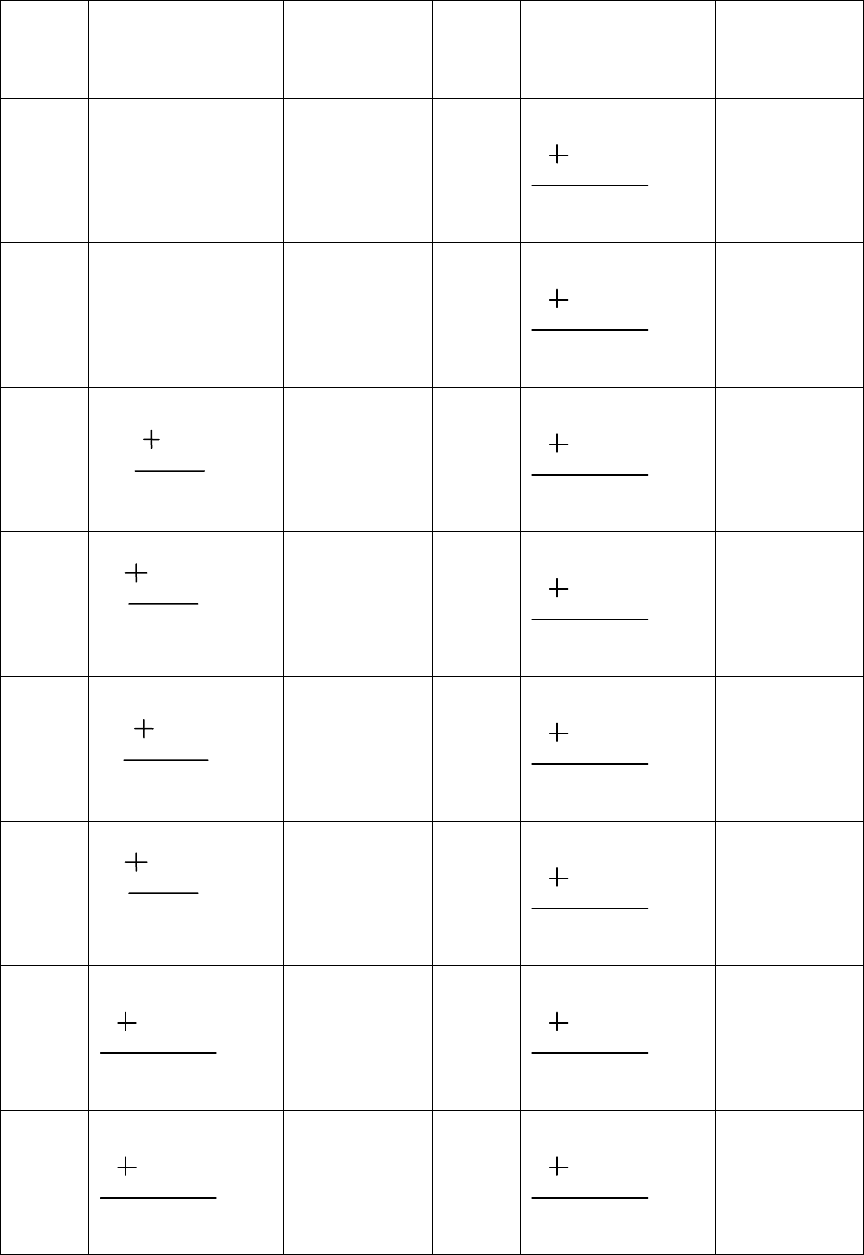
Таблица 13.
Процесс получения двоично-шестнадцатиричной таблицы
16-ая
Действие
в 2-ой
Результат
в 2-ой
16-ая
Действие в
2-ой
Результат
в 2-ой
0
16
0
2
0
2
8
16
1000
2
1
16
1
2
1
2
9
16
1001
2
2
16
10
2
A
16
1010
2
3
16
11
2
B
16
1011
2
4
16
100
2
C
16
1100
2
5
16
101
2
D
16
1101
2
6
16
110
2
E
16
1110
2
7
16
111
2
F
16
1111
2
1110
2
1
2
1111
2
1
1101
2
1
2
1110
2
1100
2
1
2
1101
2
1 1
1011
2
1
2
1100
2
1010
2
1
2
1011
2
1
1001
2
1
2
1010
2
1000
2
1
2
1001
2
1 1 1
111
2
1
2
1000
2
110
2
1
2
111
2
1
101
2
1
2
110
2
100
2
1
2
101
2
1
11
2
1
2
100
2
1
1
2
1
2
10
2
10
2
1
2
11
2
Как видим результаты, полученные увеличением каждого последующего
двоичного числа на 1, совпадают с результатами, полученными при
непосредственном переводе (таблица 12).
V тип.
Дополнительные задачи по системам счисления
Задача. Составить таблицу умножения для пятеричной системы,
используя ее найти
4302
5
• 324
5
.
Решение.
а) Составим таблицу умножения для пятеричной системы счисления:
0 • 0 = 0 • 1 = 0 • 2 = 0 • 3 = 0 • 4 = 0.
1 •
а = а, поэтому 1 • 1 = 1, 1 • 2 = 2; 1 • 3 = 3; 1 • 4 = 4.
2
5
• 2
5
= 2
10
• 2
10
= 4
10
= 4
5
.
2
5
• 3
5
= 2
10
• 3
10
= 6
10
= 1 • 5 + 1 = 11
5
.
2
5
• 4
5
= 2
10
• 4
10
= 8
10
= 1 • 5 + 3 = 13
5
.
3
5
• 3
5
= 3
10
• 3
10
= 9
10
= 1 • 5 + 4 = 14
5
.
3
5
• 4
5
= 3
10
• 4
10
= 12
10
= 2 • 5 + 2 = 22
5
.
4
5
• 4
5
= 4
10
• 4
10
= 16
10
= 3 • 5 + 1 = 31
5
.
Итак, получили таблицы 14.
Таблица 14.
Таблица умножения для пятеричной системы счисления
• 0 1 2 3 4
0
0 0 0 0 0
1
0 1 2 3 4
2
0 2 4 11 13
3
03111422
4
04132231
б) Найдем произведение 4302
5
• 324
5
, используя правила умножения
аналогичные правилам, принятым в десятичной с. с., и таблицу 14.
Запишем второй множитель под первым так, чтобы разряды совпадали:

Используя, таблицу 14, умножим 4302
5
на 4
5
.
Рассуждали так: четыре на два 13 (по таблице); 3 пишем, 1 – в уме.
Четыре на нуль дает 0, да плюс один, – пишем 1. Четыре на три 22 (по таблице);
2 пишем, 2 – в уме. Четыре на четыре 31 (по таблице), да плюс два, – пишем 3,
3 – в уме. Тройку сносим в пятый разряд.
Рассуждая аналогично, умножим 4302
5
на 2
5
, полученное произведение
запишем под первым результатом, смещая на разряд влево:
Умножим 4302
5
на 3
5
, полученное произведение запишем под вторым
результатом, смещая на разряд влево:
Сложим полученные произведения, используя правило сложения в
q-ной
системе счисления для 5-ой с. с.:
Итак, 4302
5
• 324
5
= 3120403
5
.
Ответ: 3120403
5
.
4302
5
324
5
33213
5
4302
5
324
5
4302
5
324
5
33213
5
14104
5
4302
5
324
5
33213
5
14104
5
23411
5
4302
5
324
5
33213
5
14104
5
23411
5
3120403
5
Задача. Записать наибольшее и наименьшее n-разрядные числа,
представимые в системе счисления с основанием q и перевести эти числа в
десятичную систему: n = 5, q = 4.
Решение.
Наибольшее пятиразрядное число, состоящее из 3 как максимальной цифры
четверичной системы счисления 33333
4
= 3 • 4
4
+ 3 • 4
3
+ 3 • 4
2
+ 3 • 4
1
+ 3 • 4
0
=
975
10
.
Наименьшее пятиразрядное число 10000
4
= 1 • 4
4
+ 0 • 4
3
+ 0 • 4
2
+ 0 • 4
1
+ 0 • 4
0
= 256
10
.
Ответ: 975
10
и 256
10
.
Задача. Какое максимальное десятичное положительное и минимальное
отрицательное числа можно представить в двух байтах информации?
Решение.
Два байта – это 16 бит (т. е. 2 по 8 бит), то есть это 16-тиразрядное число
в двоичной системе счисления. Положительное число начинается (слева)
нулем, так как мы ищем максимальное число, то остальные цифры будут
единицы. Итак, двоичное представление максимального положительного числа
в двух байта информации: 0111 1111 1111 1111
2
. Это число проще перевести в
16-ную систему по таблице 12, а затем из 16-ой с. с. в десятичную:
0111 1111 1111 1111
2
= 7FFF
16
= 7 • 16
3
+ 15 • 16
2
+ 15 • 16
1
+ 15 • 16
0
=
= 7 • 4096 + 15 • 256 + 15 • 16 + 15 = 28672 + 3840 + 240 + 15 = 32767
10
.
Отрицательное число начинается (слева) единицей, так как мы ищем
минимальное число, то остальные цифры будут нули. Итак, двоичное
представление минимального отрицательного числа в двух байта информации:
1000 0000 0000 0000
2
. Это число проще перевести в 16-ную систему по таблице
12, а затем из 16-ой с. с. в десятичную:
1000 0000 0000 0000
2
= 8000
16
= 8 • 16
3
+ 0 • 16
2
+ 0 • 16
1
+ 0 • 16
0
=
= 8 • 4096 + 0 + 0 + 0 = – 28672
10
.
Ответ: 32767
10
и – 28672
10
.

Задача. Получить двоичную, шестнадцатеричную форму внутреннего
представления чисел в двухбайтовой ячейке:
1608
10
и –1608
10
.
Решение.
Воспользуемся правилами получения внутреннего представления в ЭВМ
целого положительного и целого отрицательного числа
N, хранящегося в k-
разрядном машинном слове. В нашем случае машинным словом является
двухбайтное число, то есть 16-тиразрядное.
Переведем
N = 1608
10
в двоичную систему счисления, получим
11001001000
2
. Внутренне представление этого положительного числа в
двухбайтовой ячейке памяти будет следующим: 0000 0110 0100 1000.
Для нахождения шестнадцатеричной формы представления числа
воспользуемся таблицей 12 и получим 0648.
Для нахождения двоичной формы представления отрицательного числа –
1608
10
найдем обратный код положительного числа 1608
10
, для этого:
заменим 1 на 0 в его двоичном представлении (0000 0110 0100 1000):
1111 1001 1011 0111.
Прибавим к обратному коду 1:
1111 1001 1011 1000 – это внутреннее двоичное представление
отрицательного числа –1608
10
. Его шестнадцатеричная форма: F9B8.
Ответ: 0000 0110 0100 1000 и 0648;
1111 1001 1011 1000 и F9B8.
1111 1001 1011 0111
2
1
2
1 1 1
1111 1001 1011 1000
2
Задачи для самостоятельного решения
I тип.
Задача 50*.
Число, записанное в развернутой форме представить в
сокращенной форме:
ж)
1•2
4
+0•2
3
+0•2
2
+1•2
1
+1•2
0
;
з)
F•16
3
+D•16
2
+8•16
1
+0•16
0
;
и)
7•8
5
+7•8
4
+5•8
3
+0•8
2
+2•8
1
+0•8
0
;
к)
4•10
8
+9•10
7
+7•10
6
+0•10
5
+2•10
4
+1•10
3
+0•10
2
+3•10
1
+4•10
0
;
л)
2•7
2
+6•7
1
+6•7
0
;
м)
5•9
4
+4•9
3
+3•9
2
+0•9
1
+7•9
0
.
Задача 51*. Число, записанное в сокращенной форме представить в
развернутом виде:
ж)
2101
3
;
з)
BF2D
16
;
и)
544
6
;
к)
97875
10
;
л)
A3B
12
;
м) 1010011
2
.
Задача 52**. Перевести число, записанное в сокращенной форме в десятичную
систему счисления:
ж)
1100010
2
;
з)
CD5
16
;
и)
3312
4
;
к)
4774
8
;
л)
3221
5
;
м)
10947
10
.
Задача 53***. Найти ошибку в сокращенной или развернутой записи числа:
л)
104006
5
;
м)
7655
7
;
н)
1011201
2
;
