Горбатов В.А. Фундаментальные Основы Дискретной Математики. Информационная Математика

Подождите немного. Документ загружается.

§5.12. Семантическое проектирование скоростной 521

графа Gc имеет вид

1 2 3

4 5

6 7 8

—

1 1 1

1 1 1 0

—

0 0 0

1 1

—

1 0 0

1 1

—

0 0 0

1 0 1 0

—

1 1

1 0 0 0 1

—

1 0

0 0

—

0 7

0 0 1

1 0

0 - 8

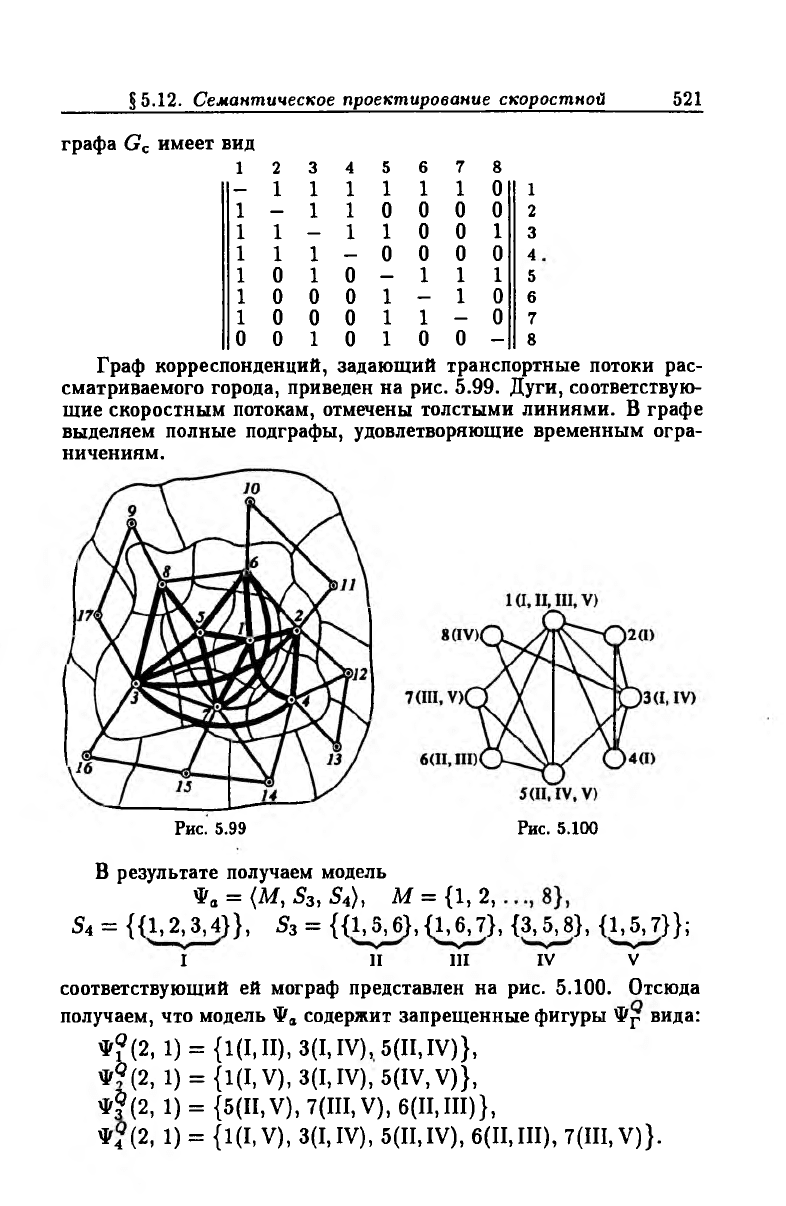
Граф корреспонденций, задающий транспортные потоки рас

сматриваемого города, приведен на рис. 5.99. Дуги, соответствую

щие скоростным потокам, отмечены толстыми линиями. В графе

выделяем полные подграфы, удовлетворяющие временным огра

ничениям.

Рис. 5.99 Рис. 5.100

В результате получаем модель

Фа = (М, 53, S4>, М = {1,2,

54 = { { М Л 4 } } , 53 = {{1Л 6}, {1Л 7}, {ЗЛ 8}, {1Л 7}};

I II III IV v

соответствующий ей мограф представлен на рис. 5.100. Отсюда

получаем, что модель Фа содержит запрещенные фигуры Фр вида:

Ф ?(2, 1) = (1(1,11), 3(1,IV), 5(11,IV)},

Ф «(2, 1) = (l(I) V), 3(1,IV), 5(IV, V)},

Ф ?(2, 1) = {5(11, V), 7(111, V), 6(11,III)},

Ф4 (2, 1) = {1(1, V), 3(1,IV), 5(11,IV), 6(11,III), 7(111, V)}.

522

Гл. 5. Прикладная теория алгоритмов

В результате выделения запрещенных фигур формируется

решетчатая таблица (табл. 5.69), столбцы которой взаимно одно

значно соответствуют запрещенным фигурам, строки — соответ

ственно их компонентам 1(1, V), 1(1,11), 3(1,IV), 5(11,IV),

5(1, V), 7(111, V), 6(11, III). Покрытие рассматриваемой таблицы

образуют строки 3 и 7. Оно является минимальным. Эти строки

Таблица 5.69

Vi(a,0)

V-f (2,1)

V-?(2,l)

^(2,1)

Ф?( 2.1)

1(1,V)

1 1

1(1,11) 1

3(1, IV)

5(Н,IV) 1 1

5(11,V) 1 1

7(111,V) 1

6(11,III) 1 1

соответствуют компонентам 3(1, IV) и 7(111, V). Для упрощения

модели Фа необходимо вычеркнуть букву 3 из слова I или IV

и букву 7 из слова III или V. Соответственно этим вычерки

ваниям имеем четыре способа упрощения модели Фа, а следо

вательно, и четыре частично квазиупорядочиваемых модели Фа,

(Р о (Ф а „ Ф ь ) = 1 ):

Фа1 = (М ,53>, 53 = { { ^ 4 } , {1Л 6}, {3 ^ 8 } , { 1 Л 7 } }

I II IV V

при вычеркивании буквы 3 из слова I и буквы 7 из слова III;

Фа2 = <М, S2, 53, S4), S4 = {{W V 4}},

53 = { { 1 1 51 6}, { M J } } ,

= {{V 8 }}

II III IV

при вычеркивании буквы 3 из слова IV и буквы 7 из слова III;

Фа, = (М, 53>, 53 = {{1Д 4}, { W > } , { W } , {ЗЛ 8}}

I II III IV

при вычеркивании буквы 3 из слова I и буквы 7 из слова V;

Фа, = {M,S2,S3,S4), s4 = {{МД4}},

5 з= { { 1 Л 6 } ,{ 1 1617>}, S2 = {{чМ } }

II III IV

при вычеркивании буквы 3 из слова IV и буквы 7 из слова V.

§5.12. Семантическое проектирование скоростной 523

В моделях Фа1 и Фа2 слово {1, 6}, а в моделях Фаз и Фа< слово

{1,5} поглощается словом {1, 5, 6}.

Каждый способ упрощения порождает запрещаемые транс

портные потоки, которые соответствуют удаляемым дугам в графе

корреспонденций при соответствующем упрощении модели Фа.

Например, вычеркивание 3 из I и 7 из III означает запрещение по

токов между следующими парами транспортных районов: (2, 3),

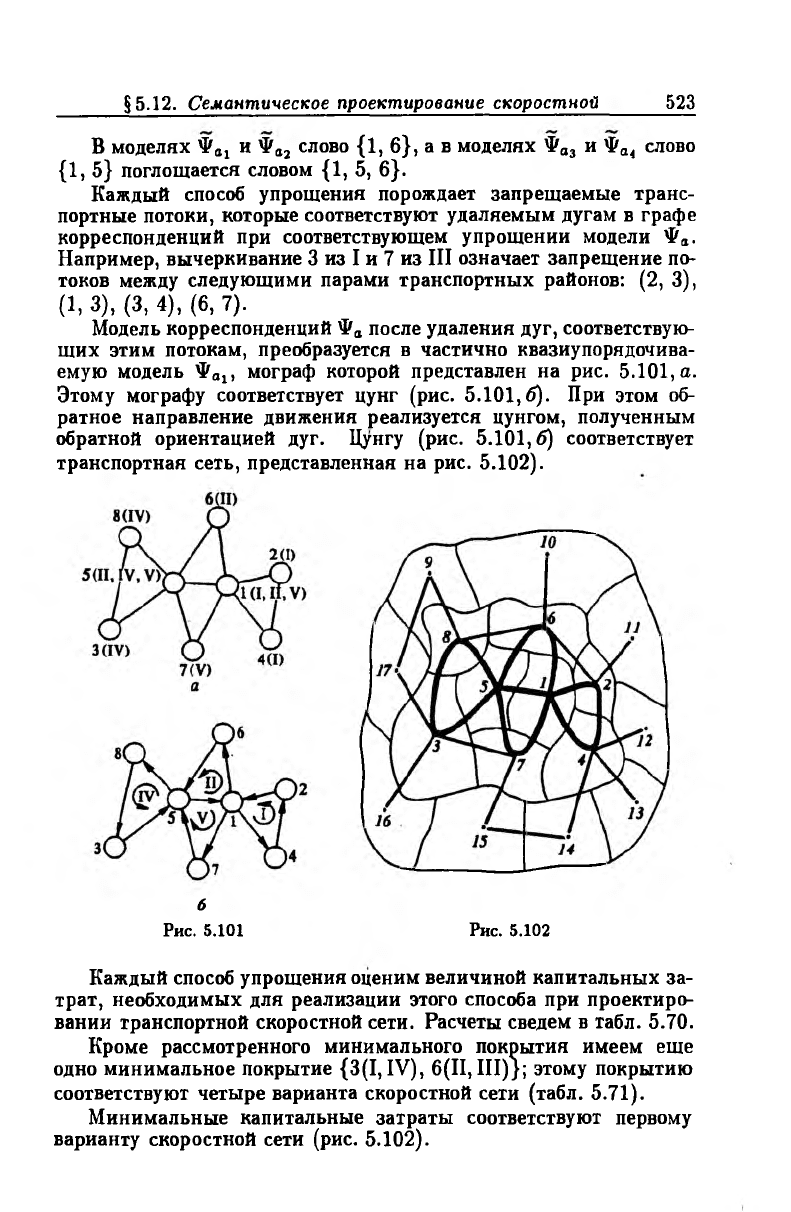
Модель корреспонденций Фа после удаления дуг, соответствую

щих этим потокам, преобразуется в частично квазиупорядочива-

емую модель Фа1, мограф которой представлен на рис. 5.101, а.

Этому мографу соответствует цунг (рис. 5.101,6). При этом об

ратное направление движения реализуется цунгом, полученным

обратной ориентацией дуг. Цунгу (рис. 5.101,6) соответствует

транспортная сеть, представленная на рис. 5.102).

Каждый способ упрощения оценим величиной капитальных за

трат, необходимых для реализации этого способа при проектиро

вании транспортной скоростной сети. Расчеты сведем в табл. 5.70.

Кроме рассмотренного минимального покрытия имеем еще

одно минимальное покрытие {3(1, IV), 6(11, III)}; этому покрытию

соответствуют четыре варианта скоростной сети (табл. 5.71).

Минимальные капитальные затраты соответствуют первому

варианту скоростной сети (рис. 5.102).

(1, 3), (3, 4), (6, 7).

Рис. 5.101 Рис. 5.102

524

Гл. 5. Прикладная теория алгоритмов

Таблица 5.70

Вычеркивание

букв на слов

Транспорт

ная сеть S

Чнсло

скрещи

ваний

Чнсло

развя-

аок

Длнна ско

ростных до

рог (км)

Капи

тальные

аатраты

(млн.

долл.)

1 3 из I, 7 из III рис. 5.102 0

300

3 из IV, 7 из III

рис. 5.103 1

2 51

380

3 3 из I, 7 из V

рис. 5.104 1 3

42 327

4 3 из I, 7 из V

рис. 5.105 4 3 58

448

Таблица 5.71

Вычеркивание

букв на слов

Транспорт

ная сеть S

Чнсло

скрещи

ваний

Чнсло

раавя-

эок

Длнна ско

ростных до

рог (км)

Капи

тальные

аатраты

(млн.

долл.)

5 3 из I, 6 из II рис. 5.106

1 3 42

327

6 3 из IV, 6 из II

рис. 5.107 3

3 53

410

7 3 из I, 6 из III рис. 5.102 0

2 40

300

8 3 из IV, 6 из III

рис. 5.103 1

2 51 380

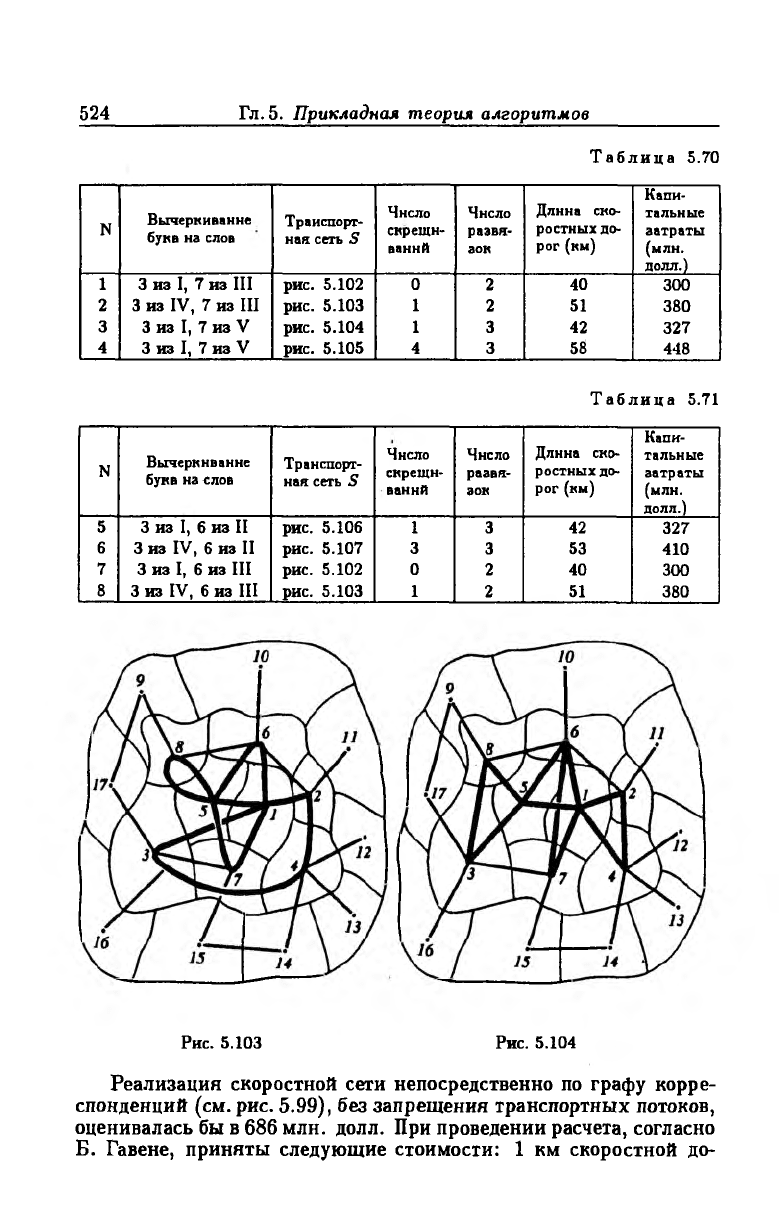
Рис. 5.103 Рис. 5.104

Реализация скоростной сети непосредственно по графу корре

спонденций (см. рис. 5.99), без запрещения транспортных потоков,

оценивалась бы в 686 млн. долл. При проведении расчета, согласно

Б. Гавене, приняты следующие стоимости: 1 км скоростной до

§5.12. Семантическое проектирование скоростной

525

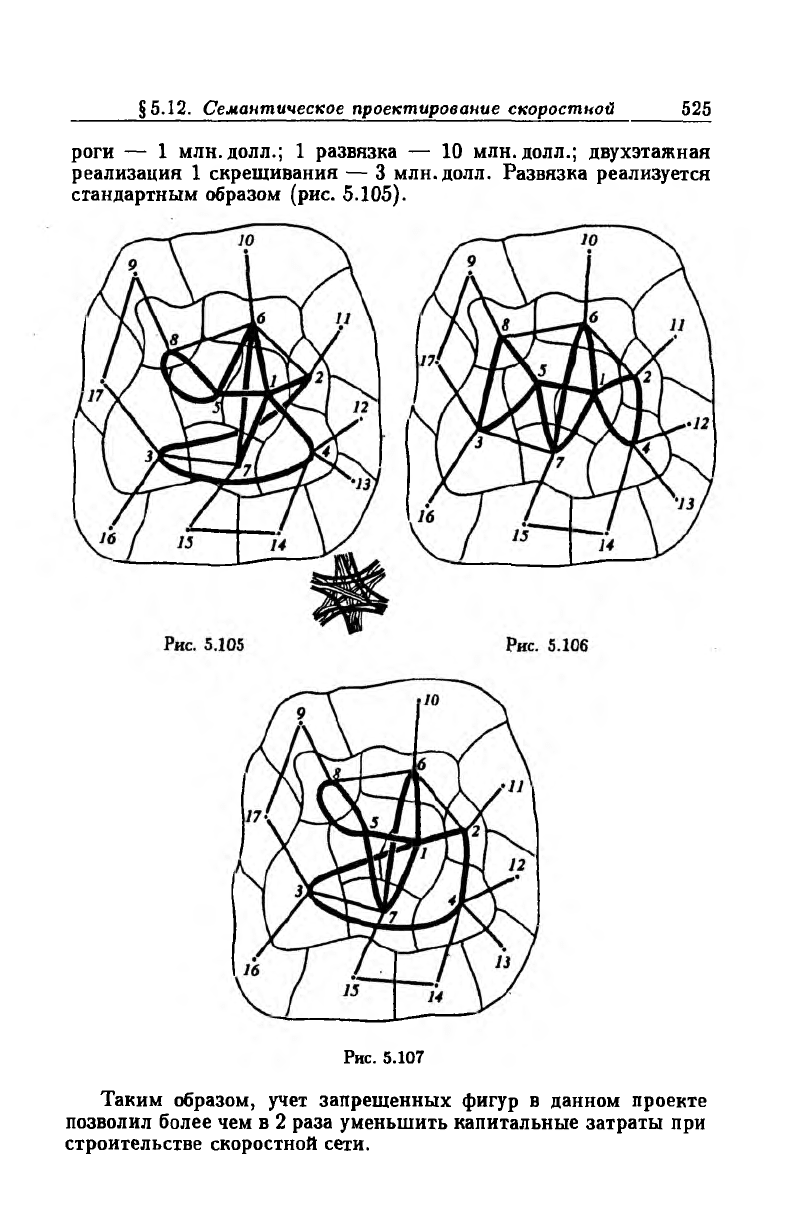
роги — 1 млн. долл.; 1 развязка — 10 млн. долл.; двухэтажная

реализация 1 скрещивания — 3 млн. долл. Развязка реализуется

стандартным образом (рис. 5.105).

Рис. 5.107

Таким образом, учет запрещенных фигур в данном проекте

позволил более чем в 2 раза уменьшить капитальные затраты при

строительстве скоростной сети.

526

Гл. 5. Прикладная теория алгоритмов

§ 5.13. Техническая диагностика сильносвязных объектов

В технической диагностике исследуемый объект представля

ется в виде одной из функциональных моделей, устанавливающих

причинно-следственные связи; при этом элементы модели явля

ются конструктивными или функциональными компонентами объ

екта [11]. Модель объекта обычно представляется в виде графа

G = (V, U),

каждая вершина которого взаимно однозначно соответствует этой

компоненте объекта, а дуга

(«,-, vj) е и

указывает на причинно-следственную связь между компонентами

t, j ; например, выход г-ro элемента связан со входом j-vo элемента

или i-й параметр входит как аргумент при вычислении j-vo пара

метра.

Процесс нахождения неисправностей элементов системы мож

но разбить на д ва этапа.

Первый этап — приведение модели объекта к диагностиру

емому виду. При произвольном числе отказавших элементов для

функциональных моделей без обратных связей существует такая

последовательность проверок, которая позволяет выявить любую

комбинацию отказавших элементов [11]. Но система без обрат

ных связей может быть частично упорядочена, т. е. представлена

как предметная интерпретация частично упорядоченных систем.

Следовательно, первая проблема — диагностируемость объекта —

сводится к семантическому эквивалентированию функциональной

модели моделью, являющейся частично упорядоченным множе

ством.

При решении этой задачи необходимо найти те дуги графа G ,

разрыв которых устраняет все сильно связные подграфы исследу

емого графа, причем суммарная стоимость всех разрывов должна

быть минимальной (обычно под суммарной стоимостью понимают

количество разрываемых дуг). Технически это осуществляется,

как показано П.П.. Пархоменко [11], организацией управляемых

разрывов обратных связей.

При проектировании программ проверки систем естественно

стремление к получению минимального числа управляемых обрат

ных связей. Решение проблемы определения минимального числа

управляемых разрывов позволит значительно снизить временные

затраты при диагностировании объекта и упростить аппаратуру

проверки.

Второй этап — диагностирование частично упорядоченной

модели объекта. После устранения всех контуров в графе функ

циональной модели, т. е. после приведения модели объекта к

§5.13. Техническая диагностика сильносвязных объектов 527

частично упорядоченному виду согласно [11], имеется такая после

довательность проверок, которая позволит выявить любую комби

нацию отказавших компонент системы. Решение задач этого этапа

не содержит принципиальных трудностей, он достаточно хорошо

изучен, имеется ряд программ диагностирования объектов этого

класса [11].

Решение задач первого этапа особенно трудоемко при диагно

стировании попарно взаимозависимых (сильносвязных) объектов,

к которым относятся автоматные сети управления химическими

процессами, энергетическими комплексами, в том числе атомны

ми электростанциями, и вообще объектами, включающими в свой

состав ряд агрегатов, в которых происходят процессы, описывае

мые сложными системами нелинейных дифференциальных урав

нений, и параметры элементов каждого агрегата попарно связаны

между собой: изменение режима работы одного из них влияет на

работу всего агрегата.

Функциональная модель объекта этого класса систем, имею

щая большое значение в промышленной автоматике, представляет

собой граф

G = (V, U),

для которого,

если (и,, V j) G U, то (uj, и,) е U.

Графы этого класса содержат большое количество контуров.

Для определения оптимального числа разрывов дуг при устра

нении контуров в графе G можно воспользоваться методами ди

намического программирования, что для практических объектов,

граф которых содержит в среднем 40-45 вершин, не реализуемо

даже на современных вычислительных машинах.

Сведение задачи первого этапа к другой модели — к задаче

покрытия двоичных таблиц, в которых каждая строка взаимно

однозначно соответствует дуге, столбец — контуру графа G, и по

крытие столбцов строками определяет искомые разрывы, — также

практически не реализуемо из-за больших размеров покрываемых

таблиц. Графы этого класса для практических объектов содержат

десятки и сотни тысяч контуров.

Для определения оптимального числа управляемых разрывов

предложим следующий метод, учитывающий временные ограни

чения на проведение технического диагностирования объекта.

Обычно эти временные ограничения задают максимальную длину

пути в графе функциональной модели, приведенной к частично

упорядоченному виду.

Предлагаемый метод проиллюстрируем диагностированием ав

томатной сети управления баковой системой, предназначенной для

уменьшения солесодержания в исходном продукте [11].

528

Гл. 5. Прикладная теория алгоритмов

Автоматная сеть G — (X , U), управляющая баковой системой,

определена матрицей смежности 5(G ):

1.1 Хя-г

х 2

Хз

Xi Xi

Xa Xl X»

Хе

Х ю

хк

0 0 0 0

0 0

х *1

0 0 0 0 0 0 0 0

Х я2

0 0 0 1

0 1

0 0 0

0 0

0 1 0 1

0 0 0 1 0

Х2

0 0 1 1 0 0 1

0 0

Хз

0 0

0 0 0

0 1 1

1 1 Xi

1 1

0 0

1 1 Xi

0 0 0

0 0

Хв

0 0 0

0 0

с XT

0 0

0 0 1 0

0 0

1 1

0 0 0 0 0

0 0 1 0 0

0 0

Xio

0 0 0

0 X K

Сеть содержит 13 автоматов: два на входе сети, x„i, х„2, устана

вливают в начальное состояние два входных контура системы, фи

нальный автомат хк управляет спуском готового продукта, осталь

ные десять автоматов, идентифицируемые как x j, х2, . ■ х10,

управляют непосредственно самим процессом уменьшения соле-

содержания.

В качестве исходной информации предлагаемого метода вы

берем граф функциональной модели и время диагностирования

объекта, которое определяет длину путей графа частично упорядо

ченной функциональной модели. В рассматриваемом случае авто

матная сеть является графом функциональной модели, при этом

компонентой модели является диагностируемый автомат. Из графа

функциональной модели удалим два начальных и финальный ав

томаты, которые не влияют на результат первого этапа, и каждый

контур длины 2 представим в виде ребра. Окончательно полу

ченный граф автоматной сети определяется матрицей смежности,

полученной из матрицы 5(G ) путем вычеркивания первых двух и

последнего столбцов (строк).

Пусть время диагностирования автоматной сети равно 5 едини

цам времени (ед. вр.); при времени функционирования при одно

кратном возбуждении автомата х,- (t = 1, 2, 3, 5, 7-10) — 1 ед. вр.;

автоматов х4, начальных и финального — по 0,5 ед. вр. Ребро

графа автоматной сети указывает на наличие причинно-следствен-

ной связи между автоматами, соответствующими концам ребра.

Предлагаемый метод состоит из двух преобразований.

Первое преобразование состоит из выделения полных подгра

фов в графе G, устанавливающем причинно-следственные связи

объекта. Объединение выделенных полных подграфов образует

граф G, и суммарное время всех вершин каждого полного подграфа

§ 5.13. Техническая диагностика сильносвязных объектов 529

не превышает заданного времени диагностирования. Выделенное

множество полных подграфов определяет модель

Фа = (Ма, 53) S4),

Ма = {*;/ г = 1, 2, ..., 10},

S3 = {{*2, *3) *9}) {*2) *3> *5}, {*1) *3, *5},

1 2 3

{xj, х5, хю}, {х4) х7) хю }},

4 5

54 “ {{*4) ®6> *8) *1о}}-

Вторым преобразованием является частичное упорядочение мо

дели Фа. Модель Фа не содержит запрещенных фигур этого пре

образования, следовательно, предикат функциональной эмерджен-

тности Р0(Фа, Фь) истинен: Ро(Фа, Фь) = 1> где Фь = (Мь, <),

Мь = Ма. В рассматриваемом случае модель Фь определяет ли

нейно упорядоченные подмножества (цепи) вида

*н1 < *з < *2 < *9 < *к,

*ш < *з < *2 < х5 < хк,

*н1 < *3 < *1 < *5 < * к ,

*н2 — Хю ^ *1 ^ Х5 < Хк ,

*н2 ^ *10 £ * 7 ^ *4 ^ Хк,

Хц2 ^ *10 < *6 ^ *8 ^ *4 ^ *к*

После построения диаграммы Хассе проводим следующие пре

образования.

1. Проводим сечение, делящее диаграмму Хассе пополам, и по

даем в места разрывов расчетные сигналы. На выходе объекта

производим измерение выходных величин. Если измеряемая ве

личина правильна, то соответствующему выходу сопоставляем 1,

в противном случае — 0.

2. Если всем выходам объекта сопоставлены 1, то рассматри

ваем диаграмму, расположенную ниже сечения. Если хотя бы од

ному выходу сопоставлен 0, то рассматриваем диаграмму, рас

положенную выше сечения, для которой выходы, помеченные О,

являются максимальными элементами, т. е. рассматриваем анти

синдром элементов, помеченных 0.

3. Если рассматриваемая диаграмма Хассе имеет носитель

мощности более 1, то переходим к п. 1; в противном случае ком

понента, соответствующая полученной вершине, неисправна.

530 Гл. 5. Прикладная теория алгоритмов

Проиллюстрируем решение этого этапа. Рассмотрим автомат

ную сеть, полученную после приведения ее к диагностируемому

виду. Проводим сечение по дугам

(х2, х9), (х2, х5), (XI, х5), (х6, х8), (х7, х4).

На выходах автоматов х4, х5, х9 получаем правильные значения:

х4 = х5 = х9 = 1. Проводим второе сечение по дугам

(*3, Х2), (Х3, Xi), (Xjo, Xj), (Х10, Хб), (х10, х7).

На выходах автоматов х2, xj, хе, х7 получаем значения, соответ

ствующие х2 = 0: xj = хе = х7 = 1. Следовательно, неисправен

автомат х2, так как х3 < xlt и, следовательно, третье сечение,

разрывающее дугу (х3, хг), реализовывать нет необходимости.

В случае, если модель Фа содержит запрещенные фигуры, их

устранение осуществляется путем сужения ее сигнатуры.

Использование предлагаемого метода в практических разработ

ках значительно уменьшает время диагностирования и упрощает

контрольную аппаратуру.

§ 5.14. Задачи и упражнения

5.1. Определить трудоемкость и емкостную сложность алгоритма синтакси

ческого эквивалентирования неориентированного графа в двудольный путем уда

ления ребер, если функционалом качества является минимум удаленных ребер.

5.2. Проверить выполнение принципа локальности для характеризационной

задачи преобразования графа в двудольный и отношения подчинения “быть под

графом” (напомним, что подграф отличается от частичного подграфа тем, что

если в ием иет какой-либо вершины графа, то иет и всех инцидентных ей в

графе ребер). Образуют ли циклы нечетной длины множество запрещенных фи-

гур?

5.3. Определить отношение подчинения, удовлетворяющее принципу локаль

ности для проблемы характеризации гамильтоновых графов.

5.4. Определить отношение подчинения, удовлетворяющее принципу локаль

ности для проблемы характеризации эйлеровых графов.

5.5. Предложить алгоритмы синтаксического, эвристического и семантиче

ского эквивалентирования неориентированных графов в эйлеровы. Сравнить

трудоемкость и емкостную сложность алгоритмов.

5.6. Выполнить семантическое эквивалентирование графа Gi, который яв

ляется дополнением графа, изображенного иа рис. 5.4, в двудольный граф

G2 = (Vj, Ui) для следующих способов преобразований запрещенных фигур

в разрешенные и функционалов качества: а) удаление из нечетного цикла ребра,

<p(Gi) = max \Ui\-, б) расщепление вершины нечетного цикла, <^(G2) = min |{/21-

5.7. Доказать, что при удалении поглощающихся строп и столбцов (см. § 5.2),

применяемом для сокращения трудоемкости нахождения покрытия семантиче

ской таблицы, минимальное решение остается.

5.8. Определить, являются ли неустойчивыми запрещенные фигуры типов

А и Б, присутствующие в мографе, приведенном иа рис. 5.10, а.

5.9. Доказать, что решение задачи теоретико-структурной минимизации

функции

/(*1, *2 , *з, i 4)|i = V(2, 3, 4, 5, 8, 9, 11, 12, 14, 15)

предложенным в § 5.4 методом, который основание функционале (5.1), абсолютно

минимально.