Горбатов В.А. Фундаментальные Основы Дискретной Математики. Информационная Математика

Подождите немного. Документ загружается.

§5.7. Решение проблемы повторной декомпозиции

461

Внутренние функции щ(хз, х4, Х5), 772(23, х4, Х5) имеют соот

ветственно вид

т(х3, х4, х5) ^ = V(7),

т{хз, х4, x5) ^ = V (l, 2, 3, 5, 6).

Для склеивания строк строим граф противоречивости Gnp(Xa)

(рис. 5.43,6); анализируя табл. 5.39, получаем

h(Gnp(Xa)) = 2, а = {0,1}, 6 = {2 ,3 }.

Склеиваем строки в табл. 5.39 согласно раскраске графа

Gnp(A'a); получаем матрицу Вейча (табл. 5.40), определяющую

Таблица 5.39 Таблица 5.40

Х 1Х 2

0 1 2 3

1 0

1 1 0

2 1 1 0

3 1 1

тъ

2 3

1 0

внешнюю функцию F((pi, щ, 772); при этом краска а кодируется

символом 0, краска b — символом 1. Получаем

¥>i(*i. x2) х = V(2, 3), F(<pi, 771, 772) = { q н а 1 | б !5’

Теорема 5.7 справедлива; получаем декомпозицию вида

f{x 1, х2, ...,xs) = F{lfii(xi, х2), т{х3, х4, х5), 772(2:3, х4, х 5)).

Утверждения (5.3)-(5.5) являются теоретико-графовым раз

витием теоремы Шеннона о разложении булевой функции по за

данным переменным и определяют построение бесповторной

декомпозиции (случай, когда Va П Vb = 0; на практике же этому

ограничению, как правило, булевы функции не удовлетворяют).

Предложим характеризационный подход, позволивший впер

вые решить проблему, поставленную К. Шенноном в 1936г. —

проблему синтеза оптимальных повторных декомпозиций системы

булевых функций заданной размерности. Подход основан на све

дении поиска декомпозиции к раскраске введенных графов проти

воречивости заданным числом красок.

Согласно характеризационному анализу запрещенными фигу

рами раскраски графа G в q красок является квазиполный граф

квазиплотности q + 1. Отсюда нетрудно доказать теорему 5.9.

462 Гл. 5. Прикладная теория алгоритмов

Теорема 5.9. Запрещенными фигурами бесповторной де

композиции булевой функции f(x i,x 2, * п) являются ква

зиполные графы Qa{qi), Qa{qi) С Gnp{Xa), и Qb{qj), Qb{qj) С

С Gnp(Xb), для которых

[l°g2 qi{Qa)} + [bg2 9j(Qb)] = n (5.6)

при совместной раскраске соответствующих графов противо

речивости.

Рассмотрим булеву функцию

f(r-i то ^ на 0, 5, 7, 9, 10, 14, 20, 21, 25, 27,

j ( Xl, * 2, ..., хь) - на ^ 4) 8) П) 12) 13) 22) 31

и разложение пространства Р(хХ2, •••,*5) в виде Р(хх2, ...

..., г5) = P(xi,xi, 13) х Р(х4, г5). Граф Кёнига, соответствующий

этому разложению, имеет вид, представленный на рис. 5.44, а.

Строчный граф противоречивости Gnp(Xa) (рис. 5.44, б) имеет

хроматическое число, равное 5, так как вершины, соответствую

щие точкам пространства 0, 1, 2, 3, 5, образуют носитель пол

ного подграфа плотности 5, а столбцевой граф противоречивости

Gnp(A'b) — хроматическое число, равное 4 (рис. 5.44, е). Следова

тельно,

[log2 5] -I- [log2 4] = 5,

и согласно утверждению (5.6) рассматриваемая функция не имеет

бесповторной декомпозиции.

Предложим стратегию построения повторных декомпозиций,

т.е. когда VaC\Vb ф 0 . Стратегия основана на редукции хромати

ческих чисел графов противоречивости Gnp(Xa), G„р{Хь) с целью

выполнения соотношения

[log2 g.-(Qa)] + [log2 qjiQb)] < П. (5.7)

Это неравенство осуществляется при сужении сигнатуры графов

противоречивости, которое в свою очередь осуществляется на осно

ве расширения носителя графа противоречивости сопряженного

§5.7. Решение проблемы повторной декомпозиции

463

подпространства за счет увеличения его размерности. Увеличе

ние размерности осуществляется с помощью «заема» переменных

из другого сопряженного пространства. Продолжим рассмотрение

примера. Синтезируем повторную декомпозицию, и в конце пара

графа оформим эту стратегию в виде соответствующих процедур.

Для выполнения соотношения (5.7) понизим хроматическое

число h(G„p(Xa)) удалением одного из ребер полного подграфа

с носителем {0, 1, 2, 3, 5} (рис. 5.45, а). Каждое ребро на этом

подграфе взвешено векторами сопряженного пространства Р(Х(,),

которыми соответствующие точки рассматриваемого пространства

Р{Х а)

сцеплены. Очевидно, что при оптимальном решении необ

ходимо удалить ребро с минимальным по мощности весом. Для

определенности удаляем ребро {1, 5}, расщепляя сцепляющий их

вектор 0 в сопряженном пространстве Р(Хь) (рис. 5.45, б) на 0' и

О". Вектор О' есть результат конкатенации

О и xi (0 = Oil), а вектор 0" — резуль

тат конкатенации,0 и Xi (0" = Oxi). Век

торы 1 и 5 в подпространстве Р (Х а) отли

чаются переменной x\: 1 — iix 2i 3, 5 —

х 1X2X3. Следовательно, инверсное ребро

{1, 0} в графе Кёнига (см. рис. 5.44, а) по

сле расщепления преобразуется в инверс

ное ребро {1, 0'}, ребро {5, 0 }— в ребро

(5, 0"} (см. рис. 5.45, б). Такое удаление

реализуется расщеплением ребра { 1, 5} в графе Gnp(-Xa)- Размер

ность пространства Р{Хь) увеличилась на единицу: Р(х4, х5) -)■

-> Р(хи £4, Х5). Хроматическое число h(Gnp(Xa)) уменьшилось

на единицу (рис. 5.46): а = {0, 4}, b = {2, 7}, с = {3}, d =

= {1, 5, 6} (a, 6, с, d — краски), и соотношение (5.7) стало вы

полняться:

[log2 4] + [log2 4] < 5.

Рассмотрим функциональную декомпозицию в подпространст

ве Р(Хь), Хь = {* i, Х4, £5}. Столбцевой граф противоречивости

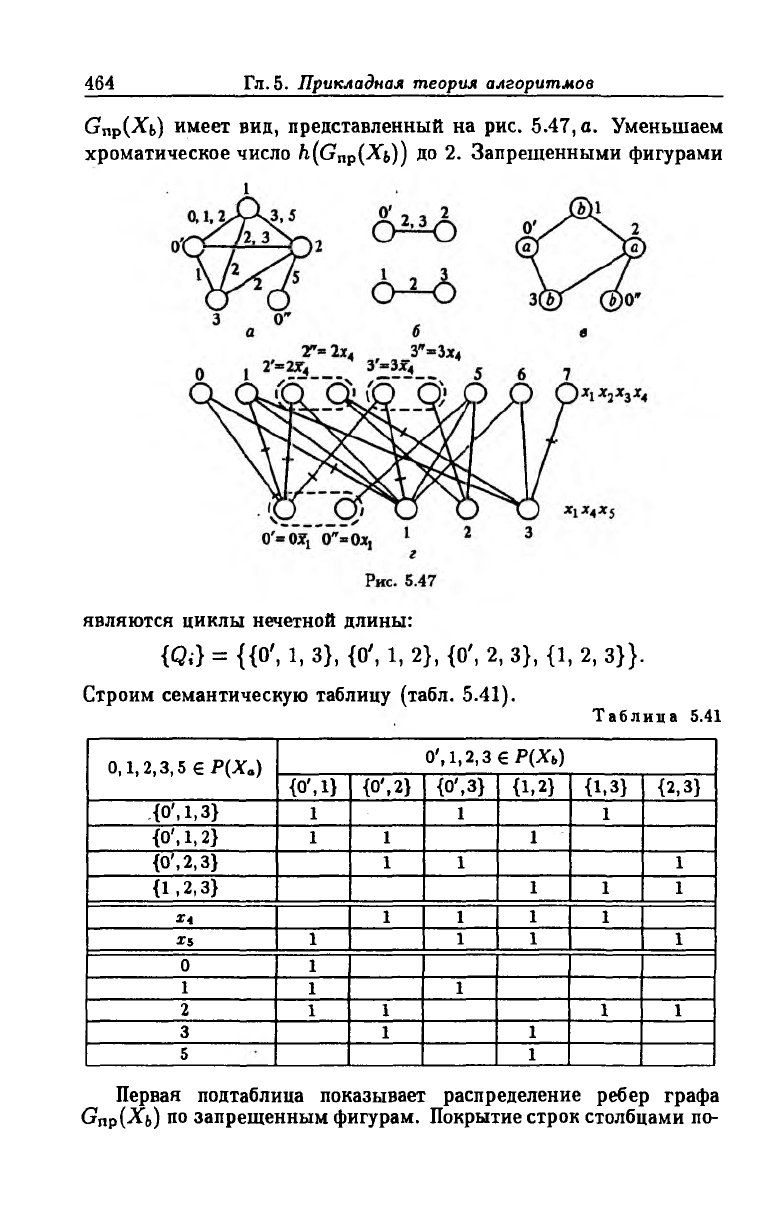
464 Гл. 5. Прикладная теория алгоритмов

Gnp(^b) имеет вид, представленный на рис. 5.47, а. Уменьшаем

хроматическое число h(Gnp(Xb)) до 2. Запрещенными фигурами

являются циклы нечетной длины:

{Qi} = {{O', 1, 3}, {O', 1, 2}, {O', 2, 3}, {1, 2, 3 }}.

Строим семантическую таблицу (табл. 5.41).

Таблица 5.41

0,1,2,3,5 € Р (Х а)

O', 1,2,3 € Р(Хь)

{ОМ}

{O', 2}

{0 ',3 }

{1 .2 }

{1 .3 }

{2 .3 }

.{O', 1,3}

i 1

{O', 1,2} i 1 1

{O', 2,3 }

1 1 1

{1 ,2 ,3 } 1

1 1

i 1 1 1

Первая подтаблица показывает распределение ребер графа

Опр(Хь) по запрещенным фигурам. Покрытие строк столбцами по-

§ 5.7. Решение проблемы повторной декомпозиции 465

называет, какие ребра необходимо удалить. Имеем три покрытия:

Вторая подтаблица показывает, какими переменными отлича

ются точки пространства Р(Хь), образующие ребро в графе

Gnp{Xb), взвешенное сцепляющими векторами Ха (третья подтаб

лица). Покрытие столбцов, составляющих покрытие первой под

таблицы, строками второй подтаблицы состоит из переменных,

с помощью которых расщепляются точки пространства Р (Х а),

соответствующие векторы которых сцепляют векторы простран

ства Р(Хь). В рассматриваемом случае пространство Р (Х а), Х а =

= Х1Х2Х3, расширяется:

— для первого покрытия ttj — переменной 15, с помощью ко

торой расщепляются точки 0, 1, 2 пространства Р (Х а)\

— для второго покрытия ТГ2 — переменной х4, с помощью ко

торой расщепляются точки 2, 3 € Р(Х а);

— для третьего покрытия 7Г3 — одной из переменной х4 или

i 5, которой расщепляются точки 1, 3, 5 € Р (Х а).

Выбираем покрытие тгг как оптимальное, так как при этом

расщепляется минимальное количество точек пространства Р (Х а)

(рис. 5.47,б,в,г). В результате размерность пространства Р (Х а),

Х а = {xi, a?2i яз}) увеличилась на 1:

размерность пространства Р(Хь), Хь = {х4, z5}, — также на 1:

Пространству Р{Х 'а) соответствует граф противоречивости

G„p{X'a) (рис. 5.48, а), пространству Р(Л *) — граф Gnp(X'b)

*i = { { 0', 1}, { 2, 3 }},

* 2 = {{O', 2}, {1 ,3 }},

^ = { { 0', 3}, { 1, 2}}.

P (X e) -► Р (Х '). Х'а = {хи х2,х 3,х4},

Р(Х Ь)->Р(Х1), Х'ь = {хи х4,х 5}.

а = {0, 2" 3", 7}

а = {0'2> ^={0", 1,3>

Ьш[1, 2', 5, 6}

с = т

Рис. 5.48

466

Di. 5. Прикладная теория алгоритмов

(рис. 5.47, в), хроматические числа которых равны h(Gnp(X'a)) =

= 3, ft(G „„T O ) = 2.

Соотношение (5.7) справедливо:

[log2 4 G „p T O )] + [log2Gnp(X0] < 5,

следовательно, функциональная декомпозиция существует. Для ее

построения раскрашиваем вершины графа Gnp(X'a):

а = (0, 2", 3", 7), Ь=?{ 1,2', 5, 6}, с = {3 '},

и вершины графа Gnp(Xh):

^ = {O', 2}, /? = {0", 1, 3}.

Кодируем краски: а — 01, о — 10, с — 11, используя функцио

нальные символы <pi<p2) и при кодировании а — 0, /? — 1 —

символ <рз. Склеивая соцветные вершины, получаем внешнюю

функцию F(<pi, у>2| <рз) (рис. 5.48, б). В результате получим функ

циональную декомпозицию вида

/(*!, х2, ...,х5) =

= F(<pi(zlt х2, х3, х4), <р2(х 1, х2, х3, г4), <р3(*1, *4, *s)),

( ч

Г 1 иа 1,2', 3', 5, б,

4>i{xu хъхз,х4) - jo на о, 2", 3", 7,

, V _ / 1 на 0, 2", 3', 3", 7,

¥?2(Х1’ *2' Хз' Х4^ ~ \ 0 на 1, 2', 5, б,

, v _ / 1 на 0", 1, 3,

<Рз{х1,х4,хъ) - | 0 на Q/) 2)

F(<Pi,<P2,<P3) = { l “ а 3, 4; б, 7.

Таблица 5.42

XIX2 X3 X4

X} Х4 Xi

ООО

100 -01 -10 -11

000-

001- 0

1 1

0100

0101

1 0

0110 0

0111 1

100-

101— 1

1 0

110—

111—

Матрица Вейча, соответствующая этой декомпозиции, имеет

вид табл. 5.42.

§5.8. Синтез функциональной декомпозиции в k-значной логике 467

§ 5.8. Синтез функциональной декомпозиции

в к-злачной логике

Обобщим найденные критерии функциональной декомпозиции

на случай fc-значной логики.

Теорема 5.10. Функция k-значной логики f(X ) декомпози

руема в виде

FfaiXa), Ы Ха), • • Ъ(Ха), ХЬ)

тогда и только тогда, когда

[logfcfc(Gnp(X .))]< | X e|, X aU X b = X, Х аГ\Хь = 0 ; (5.8)

[ ] — знак ближайшего целого числа; Gnp(A'a) — граф противо

речивости, соответствующий пространству Р (Х а), Р (Х ) =

= Р (Х а) х Р (Х Ь).

Теорема 5.11 (А.В. Горбатов). Функция k-значной логики

f(X ) декомпозируема в виде

Р(<Р!(Ха), Ы Ха), ..,<Ps(Xa), т (ХЬ), Т?2(ЛГЬ), . . 7Ь(ХЬ))

тогда и только тогда, когда

([log, h{Gnp(Xa))} < |*.|)&([logfc h{Gnp{Xb))} < |ХЬ|) (5.9)

при совместной раскраске строчного графа против оречивос-

ти G„p(Xa) и столбцевого графа противоречивости Ga р№),

Х а U Хь = X, Х аГ\Хь = 0, при представлении пространства

Р{Х ) в виде Р{Ха) х Р{ХЬ).

Теорема 5.12 (А.В. Горбатов). Функция k-значной логики

f(X ) декомпозируема в виде

F{<Pi(Xa), Ы Ха), ...,Ы Ха), т(Хь), г,2(Хь),...,г,,(Хь)),

Х аиХь = Х , Х аПХьф0,

тогда и только тогда, когда после редукции хроматических

чисел h(Gnp(Xa)) и h(G„p(Xb))

[l°gfc ?(Qa)] + [logfc q{Qb)} < \X\, (5.10)

где q(Qa) — квазиплотность редуцированного строчного гра

фа противоречивости Gnp(X a); q(Qb) — квазиплотность реду

цированного столбцевого графа противоречивости Gnp(Xb).

Рассмотрим функцию трехзначной логики

(2 на 0,2,3,23,38,43,67,68,

f ( x 1, х2, хз, * 4) = < 1 на 10,27,29,35,50,53,57,60,61,79,

(0 на 4,8,21,33,45,51,78,80.

Представим исходное пространство Р{Х) в виде произведе

ния двух сопряженных подпространств Р (Х а), Р(Хь) , Р{Х ) =

= Р{Ха) х Р{Х Ь), Х а = {ал, х2], Х ь = {х 3, г4}; тогда матрица

Вейча имеет вид табл. 5.43.

468

Гл. 5. Прикладная теория алгоритмов

Таблица 5.43

Х\Х2

Х3Х4

00 01 02 10 11

21 22

00 2 2

2 0 0

01 1

10 1 1 0

2 2

20 1 1

21 2

22 0 1 0

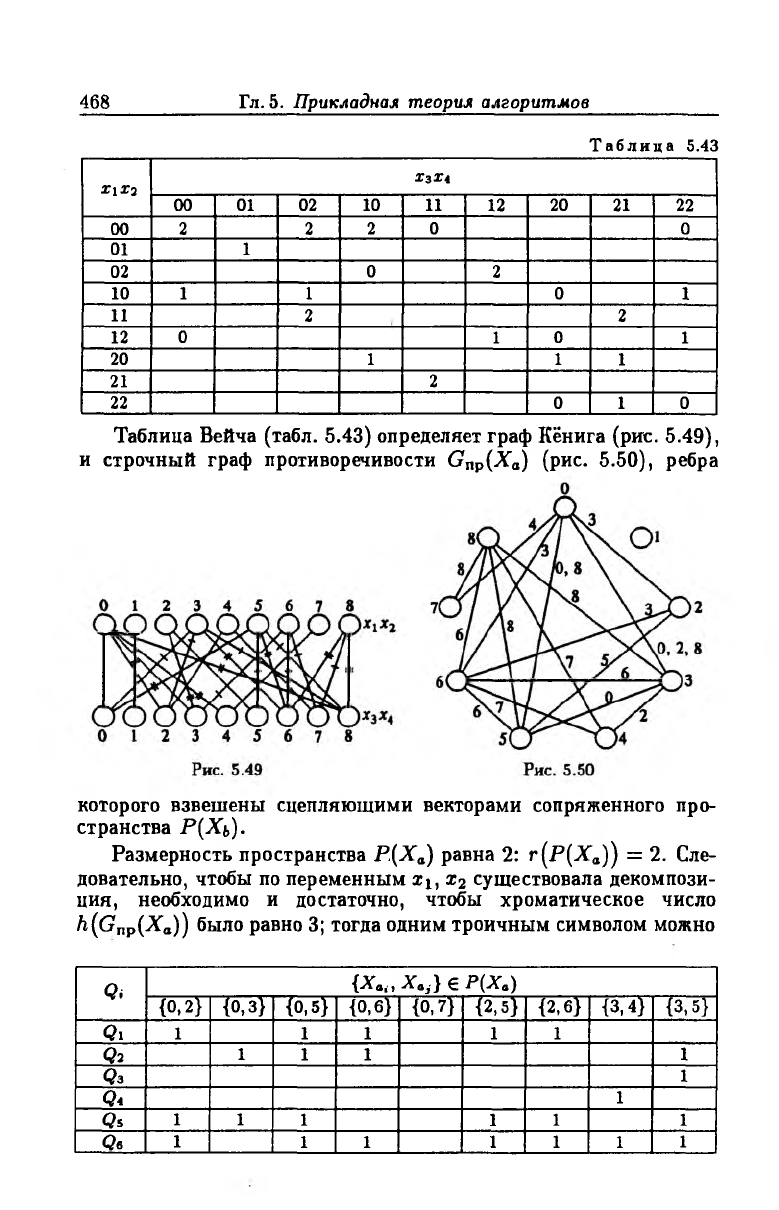
Таблица Вейча (табл. 5.43) определяет граф Кёнига (рис. 5.49),

и строчный граф противоречивости Gnp(X a) (рис. 5.50), ребра

которого взвешены сцепляющими векторами сопряженного про

странства Р(Хь).

Размерность пространства Р,(Ха) равна 2: r(P p fa)) = 2. Сле

довательно, чтобы по переменным Xi, х2 существовала декомпози

ция, необходимо и достаточно, чтобы хроматическое число

h(Gnp(Xa)) было равно 3; тогда одним троичным символом можно

{X ai, X aj) € P (X a)

{0,2}

{0,3}

{0,5}

{0,6} {0,7} {2,5} {2,6} {3,4}

{3,5}

1 1 1 1 1

1 1 1

1 1

Q»

1 1 1 1 1 1

§ 5.8. Синтез функциональной декомпозиции в k-значной логике 469

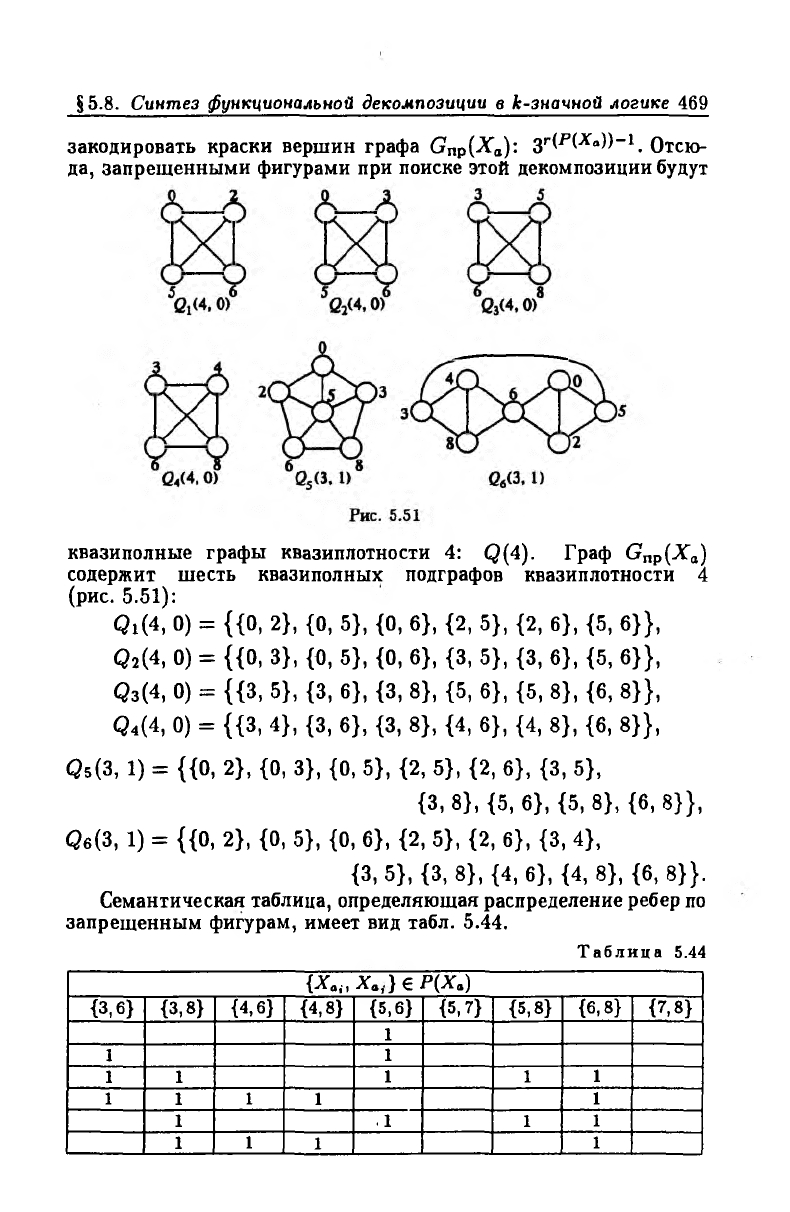
закодировать краски вершин графа GпР(Ха): S - t W » - 1. Отсю

да, запрещенными фигурами при поиске этой декомпозиции будут

квазиполные графы квазиплотности 4: Q(4). Граф Gnp(ATa)

содержит шесть квазиполных подграфов квазиплотности 4

(рис. 5.51):

Qi(4, 0) = { { 0, 2}, { 0, 5}, { 0, 6}, { 2, 5}, { 2, 6}, {5, 6}},

Q2(4, 0) = {{0 , 3}, {0, 5}, {0, 6}, {3, 5}, {3, 6}, {5, 6}},

Q3(4, 0) = {{3, 5}, {3, 6}, {3, 8}, {5, 6}, {5, 8}, { 6, 8}},

g 4(4, 0) = {{3, 4}, {3, 6}, {3, 8}, {4, 6}, {4, 8}, { 6, 8}},

g 5(3, 1) = { { 0, 2}, { 0, 3}, { 0, 5}, { 2, 5}, { 2, 6}, {3, 5},

{3, 8}, {5, 6}, {5, 8}, { 6, 8}},

g 6(3, 1) = { { 0, 2}, { 0, 5}, { 0, 6}, { 2, 5}, { 2, 6}, {3, 4},

{3, 5}, {3, 8}, {4, 6}, {4, 8}, { 6, 8}}.

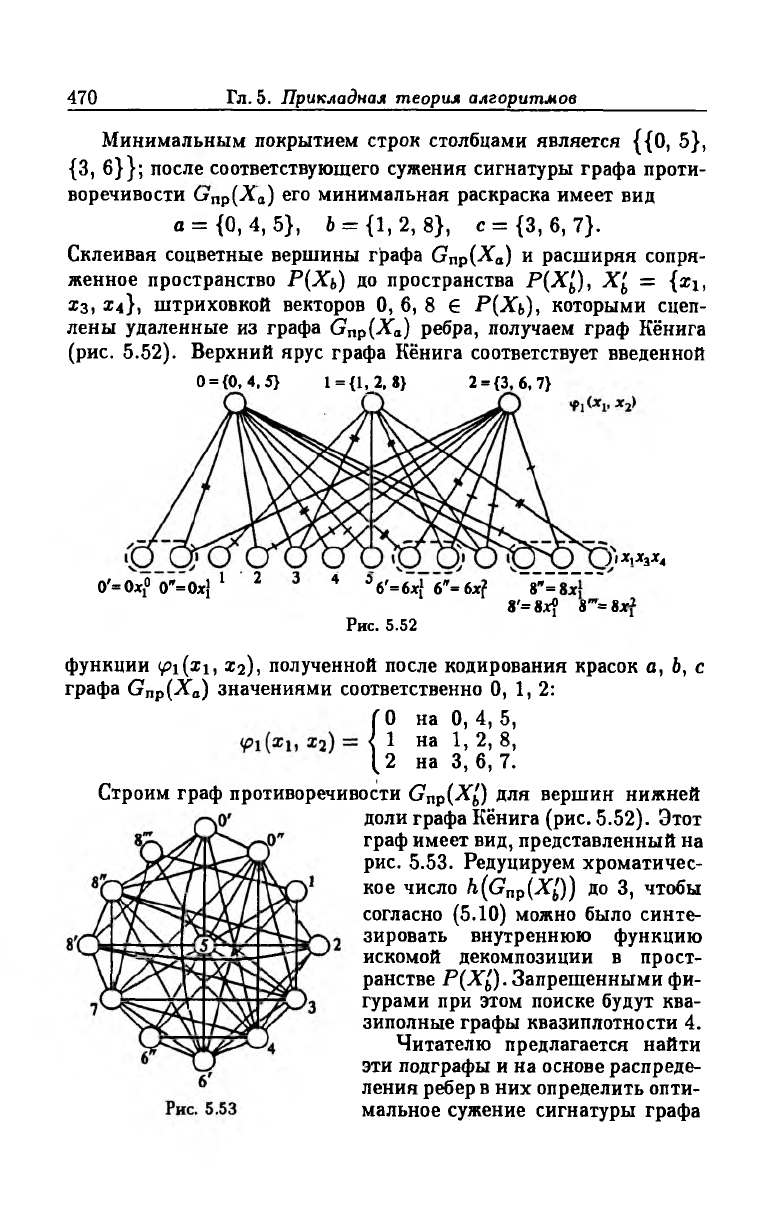
Семантическая таблица, определяющая распределение ребер по

запрещенным фигурам, имеет вид табл. 5.44.

Таблица 5.44

{X at, X .,} € Р(Хш)

{3,6}

{3,8}

{4,6}

{4,8}

{5,6}

{5,7}

{5,8} {6,8} {7,8}

1 1

1 . 1 1

470

Гл. 5. Прикладная теория алгоритмов

Минимальным покрытием строк столбцами является {{0, 5),

{3, 6}}; после соответствующего сужения сигнатуры графа проти

воречивости (тпр(.Ха) его минимальная раскраска имеет вид

a = {0,4,5}, b = {1, 2, 8}, с = {3, б, 7}.

Склеивая соцветные вершины графа Gnp(Xa) и расширяя сопря

женное пространство Р(Хь) до пространства Р{Х'Ь), Х'ь = {zj,

х3, 14}, штриховкой векторов 0, б, 8 € Р{Хь), которыми сцеп

лены удаленные из графа Gnp(Xa) ребра, получаем граф Кёнига

(рис. 5.52). Верхний ярус графа Кёнига соответствует введенной

0 = {0,4,5} 1 ={1,_2,8} 2 = {3,6,7}

0'= <Ц° 0"=0х}

1 2

)ix ,x 3x4

4 V = 6 * } б"= Ьх\ 8"=

S'= 8x4 * " ’* 8xi

Рис. 5.52

функции 4>i{xi, Х2), полученной после кодирования красок а, Ь, с

графа Gnp(X e) значениями соответственно 0, 1, 2:

{

0 на 0, 4, 5,

1 на 1, 2, 8,

2 на 3, б, 7.

Строим граф противоречивости Gn^Xl) для вершин нижней

доли графа Кёнига (рис. 5.52). Этот

граф имеет вид, представленный на

рис. 5.53. Редуцируем хроматичес

кое число h(Gnp(X(l)) до 3, чтобы

согласно (5.10) можно было синте

зировать внутреннюю функцию

искомой декомпозиции в прост

ранстве Р{Х ’Ь). Запрещенными фи

гурами при этом поиске будут ква

зиполные графы квазиплотности 4.

Читателю предлагается найти

эти подграфы и на основе распреде

ления ребер в них определить опти

мальное сужение сигнатуры графа