Горбатов В.А. Фундаментальные Основы Дискретной Математики. Информационная Математика

Подождите немного. Документ загружается.

§5.5. Характеризация разложения графа переходов________431

в j-u разряде векторы сцепленных состояний совпадают, то при

подаче на вход автомата вектора X, по которому они сцеплены,

в общем случае будет нарушена детерминированность перехода в

этом подавтомате. Следовательно, построение абстрактной парал

лельной декомпозиции автомата сводится к многокомпонентной

раскраске (мультираскраске) графа сцепления, при которой смеж

ным вершинам сопоставляют спектры красок, отличные друг от

друга в каждой компоненте.

Разложение графа переходов в частичное декартово произведе

ние не выводит результирующий граф из класса графов перехода.

Запрещенными фигурами этой семантики являются квазиполные

графы.

Теорема 5.4. Если граф сцепления, построенный для каж

дого из подавтоматов, не содержит квазиполного графа ква

зиплотности д + 1, то соответствующий автомат разложим

(декомпозируем) в частичное декартово произведение функ

ционально не связанных между собой сомножителей — под

автоматов, число состояний каждого из которых не превы

шает q.

Таким образом, квазиполные графы — запрещенные фигуры,

характеризующие достаточное условие функциональной несвязно

сти подавтоматов при поиске параллельной декомпозиции управ

ляющего автомата. В дальнейшем этот класс запрещенных фигур

будем обозначать Q*. При этом граф сцепления для первого рас

сматриваемого подавтомата представляет собой граф сцепления,

построенный по графу переходов согласно его определению. Граф

сцепления i-го подавтомата представляет собой граф сцепления

первого подавтомата, в который добавлены ребра, соединяющие

вершины с одинаковым спектром красок. Добавление этих ребер

необходимо для однозначной идентификации состояний автомата.

Рассмотрим построение абстрактной параллельной декомпози

ции автомата на основе найденной семантики на следующем при

мере.

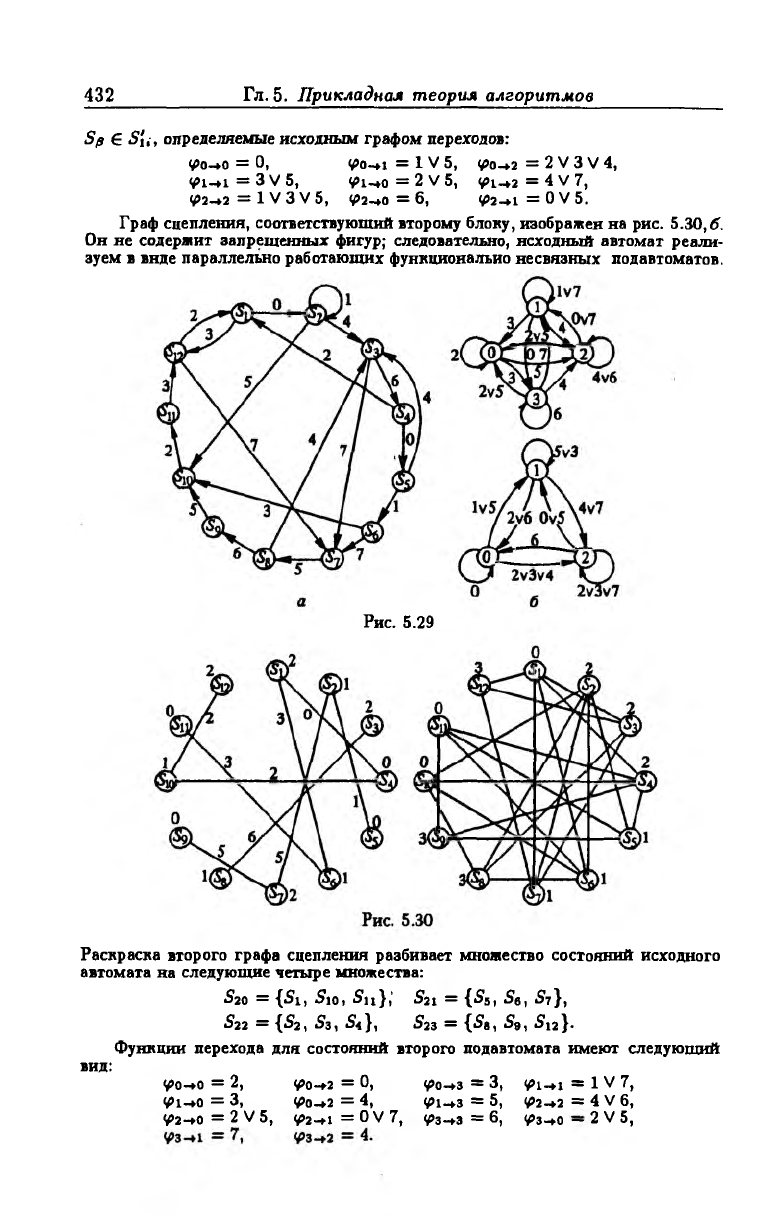
Автомат имеет три входных канала. Граф переходов изображен на

рис. 5.29, а. Входные векторы обозначены десятичными эквивалентами соответ

ствующих двоичных наборов. Найдем параллельную декомпозицию автомата в

виде двух автоматов с числом внутренних состояний соответственно 3 н 4.

Граф сцепления первого подавтомата приведен на рнс. 5.30, а. Он не со

держит запрещенных фигур; следовательно, возможна раскраска тремя цветами:

{0, 1, 2}. Каждый цвет соответствует состоянию первого подавтомата. Построим

его граф переходов G i = (И , (Ui, X )). В результате раскраски графа Gco мно

жество состояний исходного автомата разбивается иа три соцветных множества,

каждое из которых соответствует состоянию первого подавтомата. Обозначим их

соответственно 5(о, Su, 5{2. Имеем

Ss, Sg, S i t } = Sfo> {S 2 , Se, Sg, S i o } = S n , {Si, S3, S7, S 12 } = S ^ .

Отсюда условиями перехода из состояния в состояние S[j (i,j = О,

1, 2) первого блока являются условия перехода из состояния 5а € в состояние

432

Гл. 5. Прикладная теория алгоритмов

Sp € S'ti, определяемые исходным графом переходов:

<fo-+o = 0, Vo-n = 1 V 5, <fio-+ 2 = 2 V 3 V 4,

Ф1-+1 = 3 V 5, V 1-+0 = 2 V 5, Vt-»2 = 4 V 7,

V2-+2 = 1 V 3 V 5, <£2-+о = 6, <02-+1 = О V 5.

Граф сцепления, соответствующий второму блоку, изображен на рис. 5.30, б.

Он не содержит запрещенных фигур; следовательно, исходный автомат реали

зуем в виде параллельно работающих функционально несвязных подавтоматов.

Рис. 5.29

Раскраска второго графа сцепления разбивает множество состояний исходного

автомата на следующие четыре множества:

St о = {S i, Sio, 5 ц },’ Su = {5s, St, 5 7 },

S22 = {S2 , S3 , S t], S23 = {5g, S9 , Su}.

Функции перехода для состояний второго подавтомата имеют следующий

вид:

V»o-»o = 2, Va-+2 = 0, if о-»з = 3, ifii-ц = 1 V 7,

V1-+0 = 3, <£о-+2 = 4, v>i-*3 = 5, V2-+2 = 4 V 6,

V>2-*o = 2 V 5, ^ 2-»i = О V 7, ifi3-*a = 6, Фз-t-o — 2 V 5,

§ 5.5. Характеризация разложения графа переходов

433

Разложение заданного графа переходов иа функционально несвязные сомно

жители приведены на рис. 5.29, б.

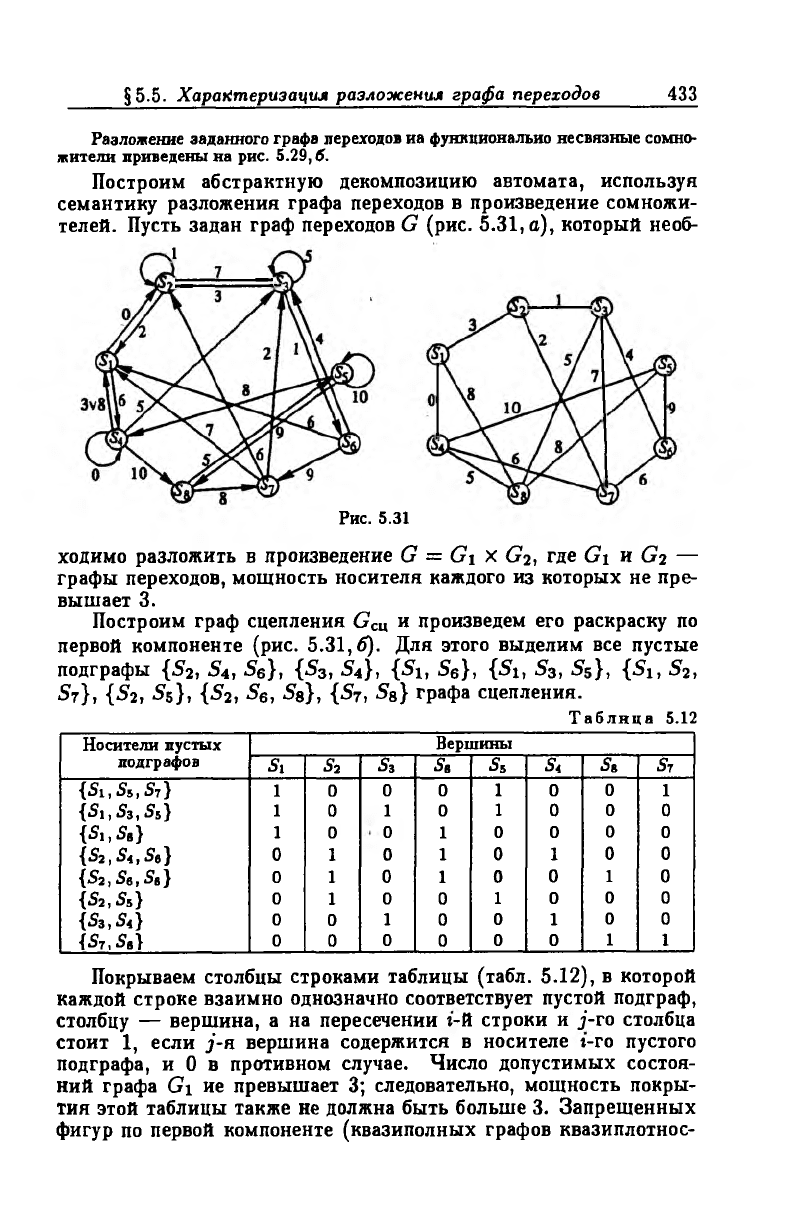
Построим абстрактную декомпозицию автомата, используя

семантику разложения графа переходов в произведение сомножи

телей. Пусть задан граф переходов G (рис. 5.31, а), который необ-

Ч1

Рис. 5.31

ходимо разложить в произведение G = G\ X G2, где Gi и G? —

графы переходов, мощность носителя каждого из которых не пре

вышает 3.

Построим граф сцепления Gcu и произведем его раскраску по

первой компоненте (рис. 5.31,6). Для этого выделим все пустые

подграфы {5 2, S4, 56}, {5 3, S4}, {Si, 56}, {Si, S3, S5}, {Si, S2,

S7), {S 2, S5}, {S 2, S6, Ss), {S7, Se} графа сцепления.

Табли ца 5.12

Носители пустых

подграфов

Вершины

s 2

S3 Se

s 5

{S i, 5s, 5 7 }

1 0

0 0 1 0

{S i, S3, S5}

1 0

{S i, Se}

1 0

0 0

{S2 ,S < ,S e}

0 1 0

1 0 1

0 0

{S 2,S 6,Se}

0 1 0 1 0

0 1 0

{5 2, S5}

1 0

{S 3,S4}

{S 7,Se}

0 0

Покрываем столбцы строками таблицы (табл. 5.12), в которой

каждой строке взаимно однозначно соответствует пустой подграф,

столбцу — вершина, а на пересечении г-й строки и jf-ro столбца

стоит 1, если j -н вершина содержится в носителе г-го пустого

подграфа, и 0 в противном случае. Число допустимых состоя

ний графа G\ ие превышает 3; следовательно, мощность покры

тия этой таблицы также не должна быть больше 3. Запрещенных

фигур по первой компоненте (квазиполных графов квазиплотнос

434

Гл. 5. Прикладная теория алгоритмов

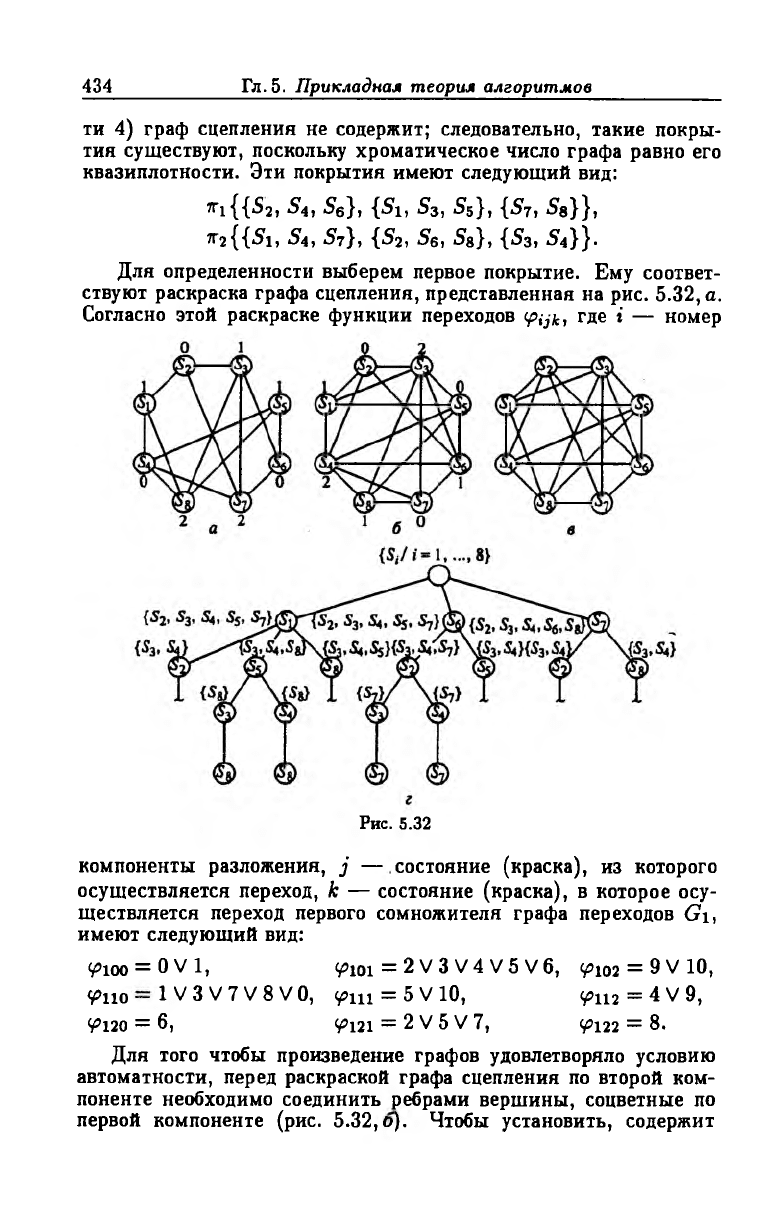
ти 4) граф сцепления не содержит; следовательно, такие покры

тия существуют, поскольку хроматическое число графа равно его

квазиплотности. Эти покрытия имеют следующий вид:

^ {{Зг, S4, S6}, {Si, 53, 5s}, {57, Se}},

* 2{{S i, S4, S7}, {S 2, S6, Ss}, {S3, S4}}.

Для определенности выберем первое покрытие. Ему соответ

ствуют раскраска графа сцепления, представленная на рис. 5.32, а.

Согласно этой раскраске функции переходов ipijk, где i — номер

Рис. 5.32

компоненты разложения, j — состояние (краска), из которого

осуществляется переход, к — состояние (краска), в которое осу

ществляется переход первого сомножителя графа переходов G1,

имеют следующий вид:

¥>100 = О V I, <pioi = 2 V 3 V 4 V 5 V6, <?io2 = 9 V 10,

фно — 1 V 3 V 7 V 8 V 0, <рт = 5 V 10, <Pii2 = 4 V 9,

¥’120 = 6, <^i2i = 2 V 5 V 7, ¥>122 = 8.

Для того чтобы произведение графов удовлетворяло условию

автоматности, перед раскраской графа сцепления по второй ком

поненте необходимо соединить ребрами вершины, соцветные по

первой компоненте (рис. 5.32,о). Чтобы установить, содержит

§ 5.5. Характеризация разложения графа переходов________435

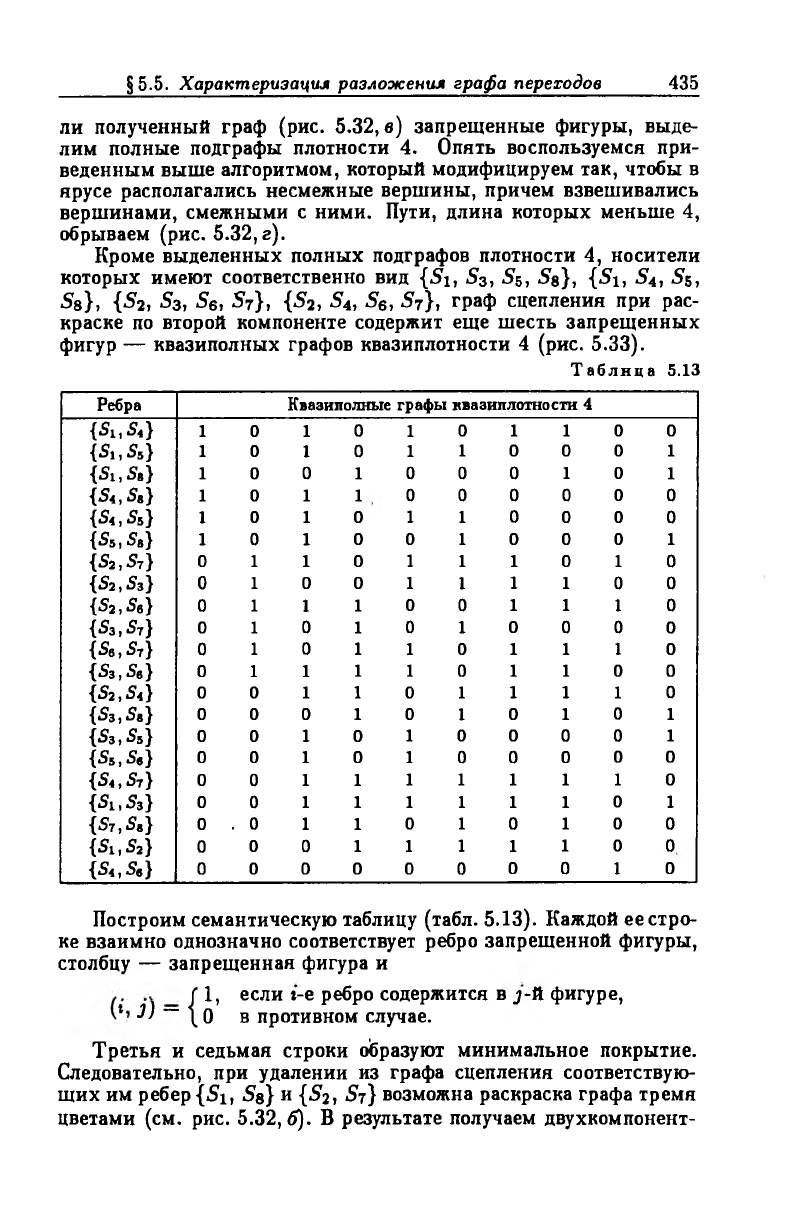
ли полученный граф (рис. 5.32, в) запрещенные фигуры, выде

лим полные подграфы плотности 4. Опять воспользуемся при

веденным выше алгоритмом, который модифицируем так, чтобы в

ярусе располагались несмежные вершины, причем взвешивались

вершинами, смежными с ними. Пути, длина которых меньше 4,

обрываем (рис. 5.32,г).

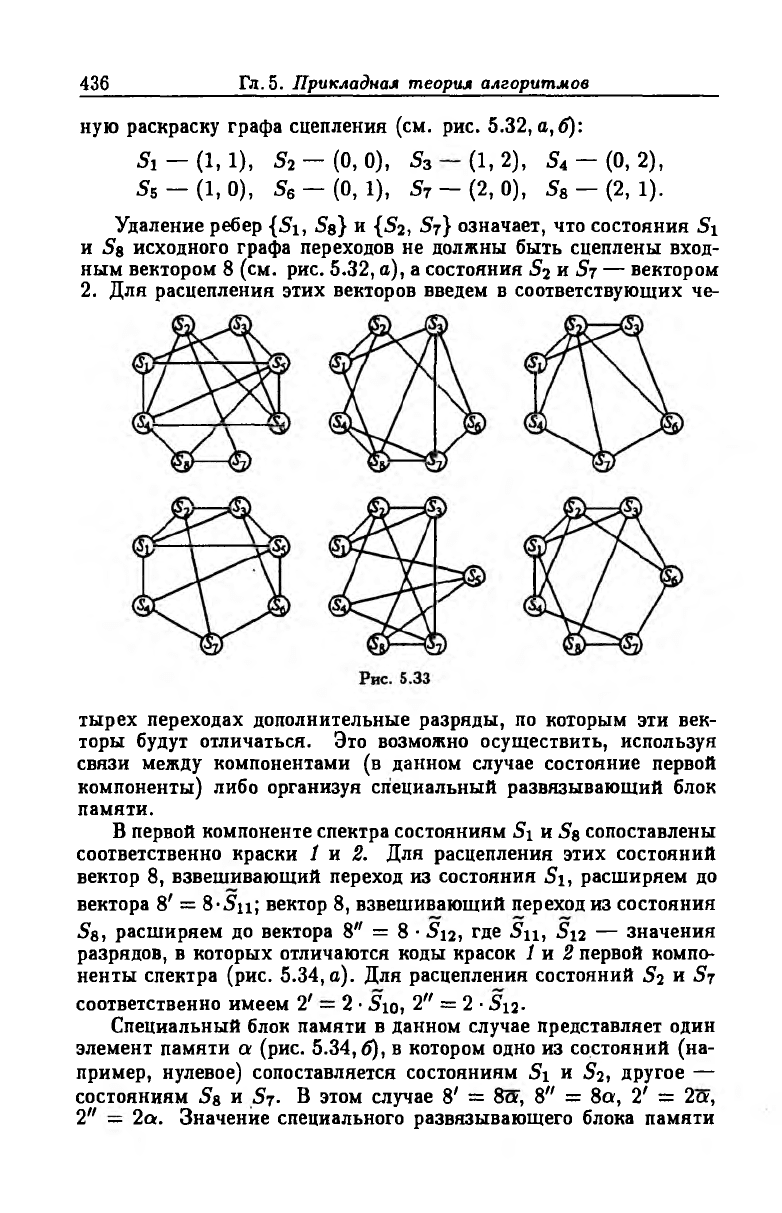
Кроме выделенных полных подграфов плотности 4, носители

которых имеют соответственно вид {Si, S3, S5, Se}, {Si, S4, S5,

Ss}, {S 2, S3, S6, S7}, {S2, S4, S6, S7}, граф сцепления при рас

краске по второй компоненте содержит еще шесть запрещенных

фигур — квазиполных графов квазиплотности 4 (рис. 5.33).

Табли ца 5.13

Ребра

Квазиполные

графы

квазиплотности 4

{s u s<}

1 0 1 0 1

0 1 1 0 0

{S .,s 5}

1 0

1 0 0 0 1

{S i.S e}

1 0 0 1 0 0 0

1 0

{5 4 ,5.} 1 0 1 1 0 0 0 0

{54, S5}

0 1 0 1 1 0 0 0

{5s, 5»}

1 0 1

0 0 1 0 0 0 1

{52,5r}

0 1 1 0 1 1 1 0 1

{S2,S3} 0

1 0 0 1

1 1

0 0

{5 2,56}

1 1

1 0

{5 3,5T} 0 1 0 1 0 1

0 0 0

{5 6,5T}

1 0 1 1 0 1 1 1 0

{5 3,56} 0 1 1

1 1

1 1 0

{5 2,54}

0 0 1 1 0 1 1 1 1 0

{5 з ,5 .}

0 0 0 1 0

0 1 0 1

{5з, Si}

0 0 1 0

1 0 0

0 0

{5 5,5 ,}

0 0 1 0 1

0 0

{54,5T} 0

1 1

1 1 1 0

{5 i,5 ,}

1 1 1 1 1 1

{5 t,5 .} 0 . 0 1 1

0 1

1 0

{5 i,5 a}

1 1 1

{54,5.} 0

0 0 0 0

0 1

Построим семантическую таблицу (табл. 5.13). Каждой ее стро

ке взаимно однозначно соответствует ребро запрещенной фигуры,

столбцу — запрещенная фигура и

Г1, если t-e ребро содержится в j -й фигуре,

3) — | о в противном случае.

Третья и седьмая строки о!бразуют минимальное покрытие.

Следовательно, при удалении из графа сцепления соответствую

щих им ребер {Si, Se} и {S 2, S7} возможна раскраска графа тремя

цветами (см. рис. 5.32,6). В результате получаем двухкомпонент

436

Гл. 5. Прикладная теория алгоритмов

ную раскраску графа сцепления (см. рис. 5.32, а,б):

5 ,— (1, 1), S2 — (0,0), S3 (1, 2), S4 — (0, 2),

S5 — (1, 0), S6 — (0, 1), S7 - (2 ,0 ), S8 — (2, 1).

Удаление ребер {Si, Ss} и {S 2, S7} означает, что состояния Si

и Ss исходного графа переходов не должны быть сцеплены вход

ным вектором 8 (см. рис. 5.32, а), а состояния S2 и S7 — вектором

2. Для расцепления этих векторов введем в соответствующих че

тырех переходах дополнительные разряды, по которым эти век

торы будут отличаться. Это возможно осуществить, используя

связи между компонентами (в данном случае состояние первой

компоненты) либо организуя специальный развязывающий блок

памяти.

В первой компоненте спектра состояниям Si и Ss сопоставлены

соответственно краски 1 и 2. Для расцепления этих состояний

вектор 8, взвешивающий переход из состояния Si, расширяем до

вектора 8' = 8-Sn; вектор 8, взвешивающий переход из состояния

Ss, расширяем до вектора 8" = 8 • S12, где Su, S12 — значения

разрядов, в которых отличаются коды красок 1 и 2 первой компо

ненты спектра (рис. 5.34, а). Для расцепления состояний S2 и S7

соответственно имеем 2' — 2 • Sю, 2" = 2 ■ S12.

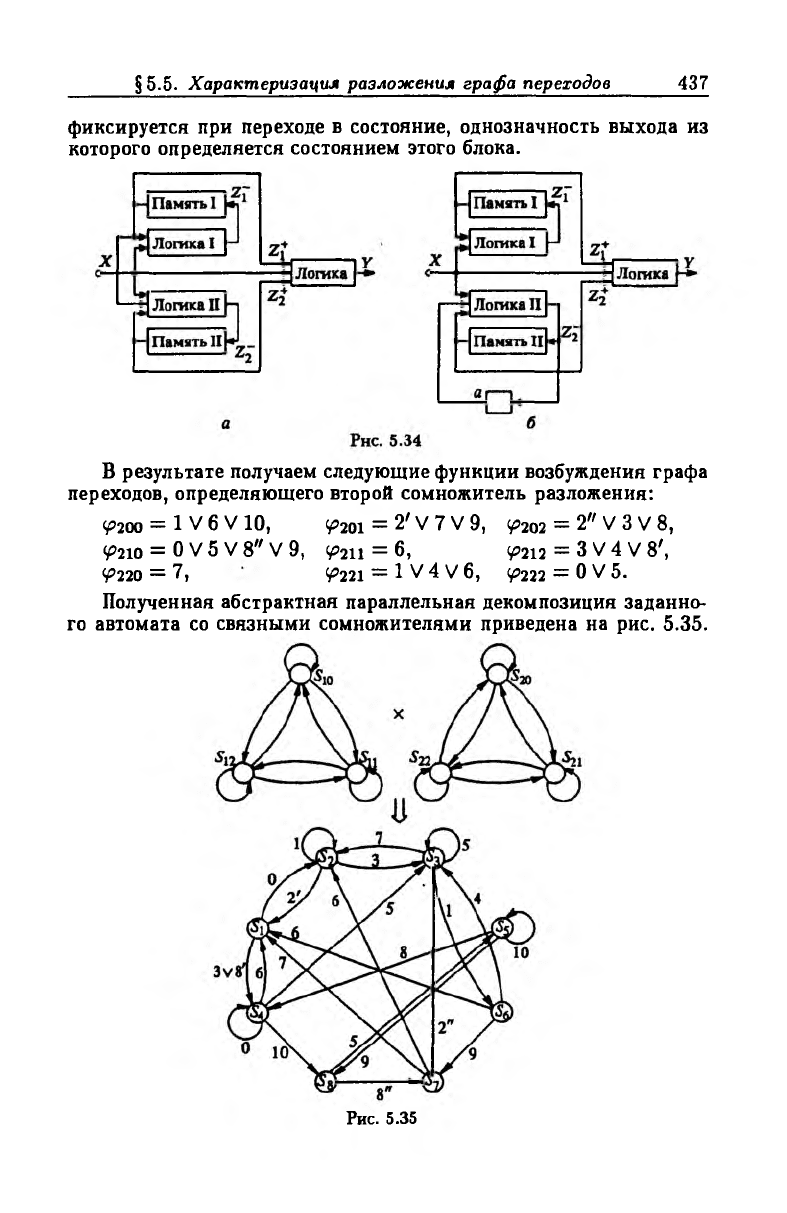
Специальный блок памяти в данном случае представляет один

элемент памяти а (рис. 5.34,6), в котором одно из состояний (на

пример, нулевое) сопоставляется состояниям Si и S2, другое —

состояниям Ss и S7. В этом случае 8' = 8а, 8" = 8а, 2' = 2а,

2" — 2а. Значение специального развязывающего блока памяти

§ 5.5. Характеризация разложения графа переходов 437

фиксируется при переходе в состояние, однозначность выхода из

которого определяется состоянием этого блока.

В результате получаем следующие функции возбуждения графа

переходов, определяющего второй сомножитель разложения:

¥>200 = 1 V 6 V 10, ¥>201 = 2' V 7 V 9, ¥>202 = 2" V 3 V 8,

^210 = О V 5 V 8;/ V 9, ^211 = 6, ^212 = 3 V 4 V 8^,

¥>220 = 7, ¥>221 = 1 V 4 V 6, ¥>222 = О V 5.

Полученная абстрактная параллельная декомпозиция заданно

го автомата со связными сомножителями приведена на рис. 5.35.

Рис. 5.35

438 Гл. 5. Прикладная теория алгоритмов

Для выяснения, возможно ли разложение рассматриваемого

автомата и частичное декартово произведение несвязных между

собой сомножителей, рассмотрим раскраску графа сцепления с уче

том характера переходов сцепленных состояний. Такой учет по

зволяет не принимать во внимание связь в графе сцепления, если

из соответствующих сцепленных состояний переход осуществля

ется в соцветные вершины. Следовательно, перед расширением

входного вектора для расцепления внутренних состояний необхо

димо проверить возможность устранения этой связи одинаковой

раскраской тех состояний, в которые сцепленные состояния пере

ходят.

Построим таблицу переходов заданного автомата (табл. 5.14),

каждой строке которой взаимно однозначно соответствует значе

ние входного вектора, столбцу — внутреннее состояние, а в клетке

(г, j) таблицы находится идентификатор внутреннего состояния,

в которое автомат переходит из j -то состояния под воздействием

г-го входного вектора.

Таблица 5.14

Si Si

5s Se 57 5.

0 s2

S3 S3

Несвязное разложение имеет место, если (согласно покрытию

семантической таблицы) связность пар {5i, Se} и {S 2, S7} не учи

тывается из-за возможностей соцветности пар вершин {S 4, S7} и

(Si, S3}. Состояния S4 и S7 сцеплены, и чтобы они были со-

цветны, необходима соцветность вершин Si и S2, в которые эти со

стояния переходят. Соцветия Si, S2 сцеплены, и чтобы они были

соцветны, необходима соцветность вершин S3 и S4. Состояния

S3, S4 не сцеплены, следовательно, могут быть соцветны. Раскра

шиваем вершины S3, S4 в один цвет. Тогда согласно свойству

транзитивности отношения соцветности получаем, что каждое из

подмножеств К0 = {Si, S2, S8}, Ki = {S3, S4, S7}, K2 = (S 5, S6}

состоит из соцветных вершин.

При найденной раскраске графа сцепления второй компоненты

разложения состояния S2, S7 являются несоцветными. Следова

тельно, и второе противоречие, обуславливающее недетерминиро

$5.6. Семантическое ослабление функциональной связности 439

ванность графа переходов второго сомножителя, также устранено.

Окончательно получаем следующие функции возбуждения второй

компоненты разложения:

<Р200 — О V 1 V 2, ^>201 = 3 V 8, ^202 = 5,

^2Ю = 6 V 7 V 10, ^211 — О V 2 V 5, ^212 == 1)

<р220 = 6 V 9, ^221 = 4 V 8, ^222 = Ю.

Таким образом, имеем несвязное разложение заданного авто

мата, определяемое полученными системами и двухкомпоиеитной

раскраской вида

5 !- (1 , 0 ), 5 4 -(0 ,1 ), 5 т- (2 ,1 ), 52 - (0 ,0 ),

55 — (1, 2), 58 - ( 2, 0), S3 - (1 ,1 ), 56 (0, 2).

В общем случае для построения параллельной абстрактной де

композиции абсолютно минимальной связности необходимо

оценить каждую раскраску по первой компоненте раскрасками по

второй и выбрать многокомпонентную раскраску, удовлетворяю

щую заданным количествам вершин графов сомножителей и их

условиям связности. Разложение графа переходов на п компонент

аналогично.

§ 5.6. Семантическое ослабление

функциональной связности памяти автомата

Рассмотрим предельную параллельную абстрактную декомпо

зицию автоматов, когда подавтоматом является элемент памяти.

Семантика этой декомпозиции будет семантикой функциональной

связности элементов памяти. С учетом структуры квазиполных

графов и двузначности булевой логики рефлексивная семантика

функциональной связности элементов памяти автомата определя

ется следующим утверждением.

Теорем а 5.5. Графы сцепления, не содержащие циклов не

четной длины, определяют кодирование, при котором элемен

ты памяти функционально несвязны.

Этот критерий позволяет последовательно определять значения

разрядов в кодах внутренних состояний аналогично тому, как это

делалось при поиске параллельной абстрактной декомпозиции.

Рассмотрим семантическое кодирование внутренних состоя

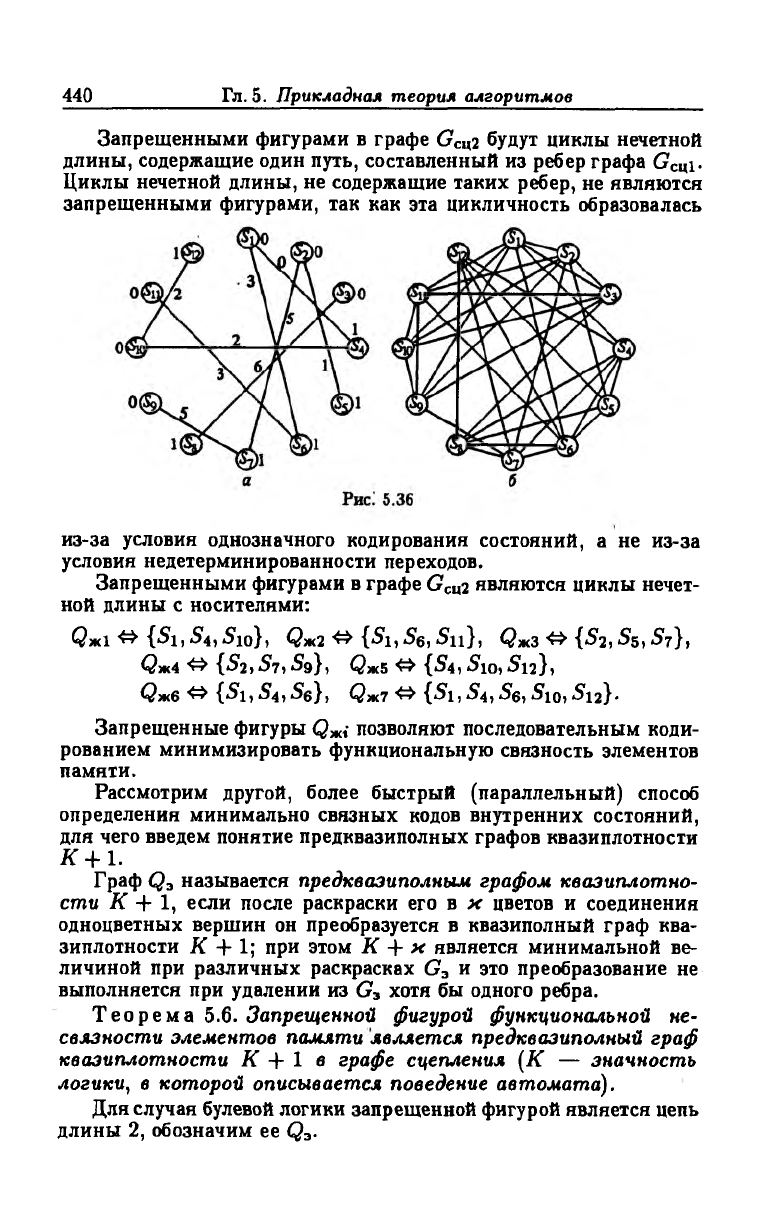
ний автомата, заданного графом переходов G (см. рис. 5.29,а).

Граф сцепления Gclx\ для первой внутренней переменной Z\, пред

ставленный на рис. 5.23, а, не содержит запрещенных фигур —

циклов нечетной длины. Кодирование по первой переменной Z\

заключается в раскраске двумя цветами, 0 и 1, вершин графа сцеп

ления Gca. 1 (рис. 5.36, а). Строим граф сцепления Gcu2 для второй

переменной Z2, Для чего соединяем ребром соцветные вершины

графа сцепления (рис. 5.36, б).

440 Гл. 5. Прикладная теория алгоритмов

Запрещенными фигурами в графе (7СЦ2 будут циклы нечетной

длины, содержащие один путь, составленный из ребер графа Gclfi-

Циклы нечетной длины, не содержащие таких ребер, не являются

запрещенными фигурами, так как эта цикличность образовалась

из-за условия однозначного кодирования состояний, а не из-за

условия недетерминированности переходов.

Запрещенными фигурами в графе Gcu2 являются циклы нечет

ной длины с носителями:

Q * i^ { S i,S 4,S10}, Q*i2 ^ {Si, Sg, Su}, фжз ^ {S2, S5, S7},

Q>k4 ^ {S2, S7, Sg}, Q }к5 <=> {S4, Sio, S12},

Qjk6 ^ {Si, S4, Sg}, Qjk7 ^ {Si, S4, Sg, S10, Sl2}.

Запрещенные фигуры фж,- позволяют последовательным коди

рованием минимизировать функциональную связность элементов

памяти.

Рассмотрим другой, более быстрый (параллельный) способ

определения минимально связных кодов внутренних состояний,

для чего введем понятие предквазиполных графов квазиплотности

К + 1.

Граф Q3 называется предкеазиполным графом квазиплотно

сти К + 1, если после раскраски его в х цветов и соединения

одноцветных вершин он преобразуется в квазиполный граф ква

зиплотности К + 1; при этом К + х является минимальной ве

личиной при различных раскрасках G3 и это преобразование не

выполняется при удалении из G3 хотя бы одного ребра.

Теорема 5.6. Запрещенной фигурой функциональной не

связности элементов памяти является предквазиполный граф

квазиплотности К + 1 в графе сцепления (К — значностъ

логики, в которой описывается поведение автомата).

Для случая булевой логики запрещенной фигурой является цепь

длины 2, обозначим ее Q3.