Горбатов В.А. Фундаментальные Основы Дискретной Математики. Информационная Математика

Подождите немного. Документ загружается.

§5.1. Принципы характеризационного анализа 401

Т аб лица 5.1

крытие столбцов строками семантической таблицы определяет ми

нимальное по включению множество преобразований, которые не

обходимо выполнить для получения из Фа модели Фа, обладаю

щей свойством Sa. Учитывая, что каждый способ преобразования

может иметь собственную стоимость, делаем вывод, что для до

стижения экстремума <^(Фь) необходимо найти минимальное по

стоимости покрытие семантической таблицы.

Рассмотрим задачу семантического эквивалентирования гра

фа, изображенного на рис. 5.6, б, в двудольный. Функционал ка

чества определяется минимальным числом удаленных ребер. За

прещенные фигуры (циклы нечетной длины) образованы следую

щими множествами ребер: Ф31 = {а, Ь, с}, Ф32 = {a, b, d, е, /}.

Способ преобразования — удаление ребра — имеет стоимость 1;

конкретный способ преобразования обозначим указанием удаляе

мого ребра. Семантическая таблица имеет вид табл. 5.1.

Минимальным является, например, по

крытие ж = {о}. Следовательно, удаляя ре

бро а, получаем двудольйый граф (рис. 5.6,в);

при этом достигнут минимум ¥>(Фь) = 1.

В общем случае способ преобразования

может быть связан не с элементами носителя

или сигнатуры модели, а с некоторыми ее

компонентами. Поэтому в общем случае се

мантическое эквивалентирование предпола

гает построение иерархической системы таб

лиц некоторой глубины к, определяемой количеством уровней в

способах преобразований. Покрытие столбцов строками первой та

блицы указывает, какие компоненты запрещенных фигур должны

быть изменены при приведении модели Фа к интерпретируемому

в терминах модели Фь виду. Опре

деление подкомпонент, которые

надо изменить для изменения най

денных на предыдущем шаге ком

понент, сводится к покрытию вто

рой таблицы, построенной ана

логично, и т. д. до построения

к-й таблицы, строки или столбцы

которой соответствуют элементам

носителя или сигнатуры, которые

необходимо изменить при приве

дении модели Фа к интерпретиру

емому в терминах модели Фь виду

(рис. 5.9).

Для определения минимально

го числа элементов носителя или

*3! Фз,

Рис. 5.9

сигнатуры, соответствующих

элементам к-й таблицы, необходима генерация всех множеств,

402

Гл. 5. Прикладная теория алгоритмов

каждое из которых состоит из покрываемых строк (столбцов) в

последней, fc-й таблице. Эта генерация соответствует перебору

всех покрытий (к — 1)-й таблицы. Для получения всех покрытий

(к — 1)-й таблицы необходима генерация всех покрытий (к — 2)-й

таблицы и т. д. Таким образом, для нахождения минимального

решения необходим перебор всех сочетаний покрытий первых fc — 1

таблиц. Эта процедура принципиально содержит перебор. Таким

образом, определение сложности решения является минимальным

по трудоемкости стандартным процессом. Этот процесс на много

порядков менее трудоемок, чем процесс фактической генерации

всех эквивалентных структур при поиске минимального решения

синтаксическим эквивалентированием.

Способы преобразования запрещенных фигур, будучи по отно

шению к ним однозначными, по отношению к модели в целом

могут быть как однозначными, так и неоднозначными. Напри

мер, способ преобразования запрещенных фигур для двудольного

графа (нечетных циклов), основанный на удалении ребра, одно

значен и для модели в целом. Рассмотрим способ преобразова

ния нечетных циклов, заключающийся в расщеплении одной из

вершин v на две несмежные вершины v и v1, каждая из кото

рых инцидентна одному из двух ребер i и у расщепляемой вер

шины (рис. 5.10, а); обозначим способ преобразования как v(x, у).

<$И-©

Рнс. 5.10

Этот способ преобразования используется в семантическом эквива-

лентировании при декомпозиции информационной системы с тре

бованием максимального быстродействия, т. е. максимального

параллелизма обработки информации. Такое требование обуслав

ливает размещение всех разделов данных, соответствующих смеж

ным вершинам, на разных дисках, т. е. приводит к дублированию

некоторых разделов. Данный способ преобразования запрещенной

фигуры для модели в целом (графа) не однозначен. Дело в том,

§5.1. Принципы характеризационного анализа

403

что преобразование запрещенной фигуры при расщеплении вер

шины v, инцидентной ребрам хну, фиксирует только то, что

новая вершина v инцидентна ребру х, а новая вершина v' — ре

бру у. Для графа в целом это означает расщепление вершины v на

и и и' с соответствующим разбиением окрестности Ги (рис. 5.10),

при котором х и у попадают в разные новые окрестности.

Рассматриваемый способ преобразования не указывает распре

деления всех вершин по новым окрестностям. Семантическая

таблица для графа (см. рис. 5.6, б) при

таком способе преобразования имеет вид

табл. 5.2

В случае неоднозначных способов пре

образований необходимо проверить все

покрытия семантической таблицы. Рас

смотрим три покрытия: 7Ti = {ui(a,6)},

я-2 = {v2(b,c), v2(b,f)}, 7Г3 = {щ(а, с),

,«3 (е, /)}. Первое покрытие, имеющее ми

нимальную мощность, дает минимальное

решение (рис. 5.10,6). Но и второе покрытие, имеющее мини

мальную мощность, также определяет минимальное решение. Оба

Преобразования, входящие в ж2, расщепляют v2. Ответ на во

прос, сколько новых вершин дают эти расщепления вместе, дают

построение и раскраска специального графа, который построен

на множестве ребер, инцидентных v2 (рис. 5.10,в). Раскраска

графа {6}, {с, /} определяет число вершин после расщепления

,и разбиение окрестности Ги2. Полученное решение минимально

(рис. 5.10,г). Преобразование, соответствующее л-3 (рис. 5.10,д),

не минимально.

Таким образом, если применяются способы преобразований,

неоднозначные для модели в целом, то необходимо для каждого

покрытия строить специальные графы и определять их минималь

ную раскраску. Поэтому особенно актуальны оценки хроматиче

ского числа графа (см. гл. 3), которые позволяют быстро отсе

ять большую часть покрытий, соответствующих графам с боль

шим хроматическим числом. Важны также “быстрые” методы

раскраски графов. В целом семантическое эквивалентирование

:Дри минимальном (неизбежном) переборе позволяет получить аб

солютно оптимальное решение.

На основе семантического эквивалентирования получаем двух-

Контурную структуру быстродействующего пакета прикладных

^Программ (рис. 5.11), в котором с помощью модуля “Характер”

Происходит автоматическая настройка на оптимальную стратегию

!*ри проведении преобразования Фа —)• Фь. Это придает “интел

лектуальность” пакету прикладных программ и позволяет отнести

Подобные пакеты к классу систем искусственного интеллекта.

*3!

fi (а,Ъ)

v2(b,c)

vs(а,с)

V2 (Ь,/)

*>з (е, /)

v4(«J, е) 1

vs(a,d)

404 Гл. 5. Прикладная теория алгоритмов

В предыдущих главах были рассмотрены характеризационные

проблемы вложения графа в плоскость, в булево пространство,

характеризации параллельно-последовательной структуры диаг-

Рис. 5.11

раммы Хассе, раскраски графов, частичного упорядочения могра

фа, проектирования логических схем в несвязных базисах.

Остановимся теперь на характеризационных проблемах, в том

числе на проблемах проектирования многовыходных логических

схем, разложения графа переходов в частичное декартово произве

дение, а также на характеризационных проблемах, возникающих

при проектировании оптимальных размещений данных в инфор

мационных системах. Характеризация моделей позволяет выя

вить объективные причины, определяющие сложность решения и

трудоемкость его поиска.

§ 5.2. Характеризация И методы оптимального

размещения данных в памяти ЭВМ

Для современных информационных систем характерны не

только большие объемы, но и сложность хранимых данных. Слож

ность данных проявляется в том, что они находятся в различных

взаимосвязях. Таким образом, сложные данные представляются в

виде набора некоторых элементарных объектов и совокупности о1

ношений, связывающих объекты данных. Иначе говоря, сложные

информационные системы формализуются такими понятиями, как

граф и мограф. Это подтверждается богатым практическим опы

том построения информационных систем.

Часто возникает необходимость хранить в “чистом виде” гра

фовые структуры, например, при использовании в базах данных

моделей данных, основанных на графах. Объекты данных хра

нятся отдельно от своих связей, которые представляются графом.

Иавестно несколько способов задания графов: с помощью матриц

инциденций и смежности, перечислением окрестностей вершин.

Можно показать, что последний способ наиболее экономичен при

больших размерностях графов, что характерно для практики. Но

задание графа перечислением окрестностей равносильно заданию

мографа, носителем которого является носитель графа, а слова

ми — окрестности его вершин. Возможны варианты в задании

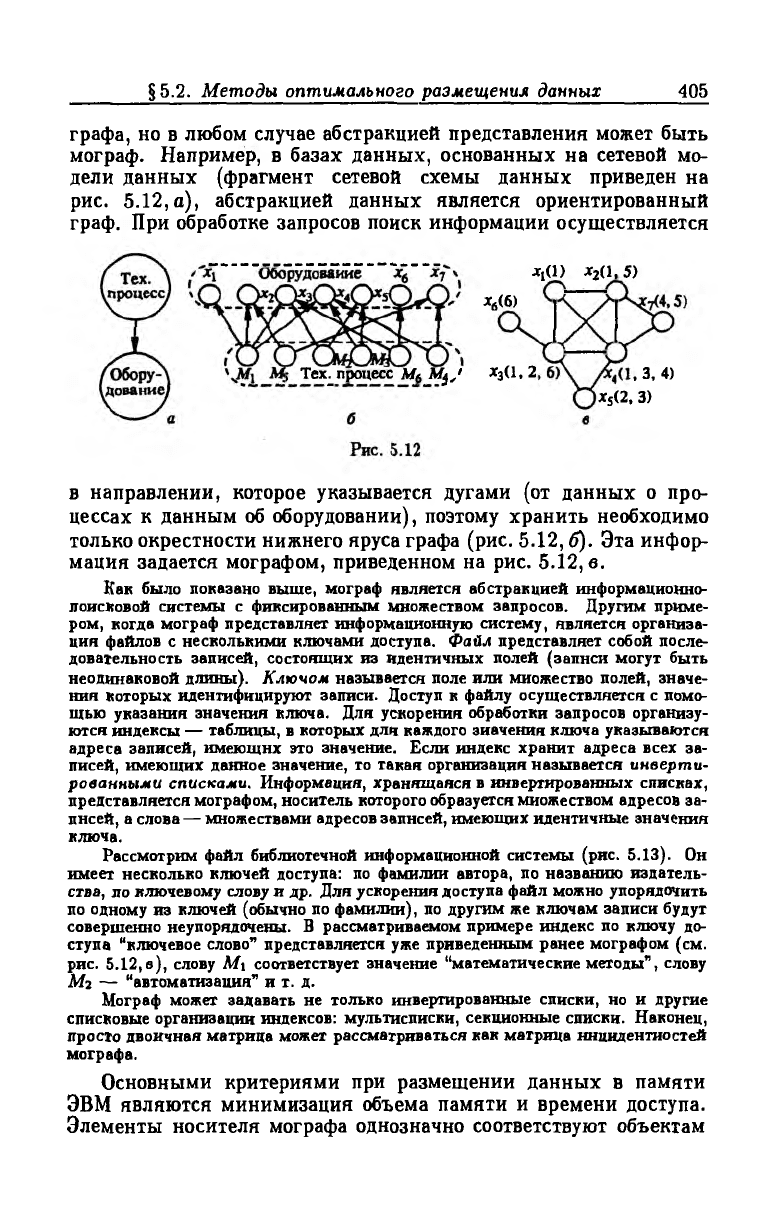
§5.2. Методы оптимального размещения данных

405

графа, но в любом случае абстракцией представления может быть

мограф. Например, в базах данных, основанных на сетевой мо

дели данных (фрагмент сетевой схемы данных приведен на

рис. 5.12, а), абстракцией данных является ориентированный

граф. При обработке запросов поиск информации осуществляется

*i(D *2о , 5 )

V6)

; Тех^процесс М й M jy' *з(1 , 2,

,3,4)

xs(2, 3)

в направлении, которое указывается дугами (от данных о про

цессах к данным об оборудовании), поэтому хранить необходимо

только окрестности нижнего яруса графа (рис. 5.12, б). Эта инфор

мация задается мографом, приведенном на рис. 5.12, в.

Как было показано выше, мограф является абстракцией информационно-

поисковой системы с фиксированным множеством запросов. Другим приме

ром, когда мограф представляет информационную систему, является организа

ция файлов с несколькими ключами доступа. Файл представляет собой после

довательность записей, состоящих из идентичных полей (записи могут быть

неодинаковой длины). Ключом называется поле или множество полей, значе

ния которых идентифицируют записи. Доступ к файлу осуществляется с помо

щью указания значения ключа. Для ускорения обработки запросов организу

ются индексы — таблицы, в которых для каждого значения ключа указываются

адреса записей, имеющих это значение. Если индекс хранит адреса всех за

писей, имеющих данное значение, то такая организация называется

инверти

рованными списками. Информация, хранящаяся в инвертированных списках,

представляется мографом, носитель которого образуется множеством адресов за

писей, а слова — множествами адресов записей, имеющих идентичные значения

ключа.

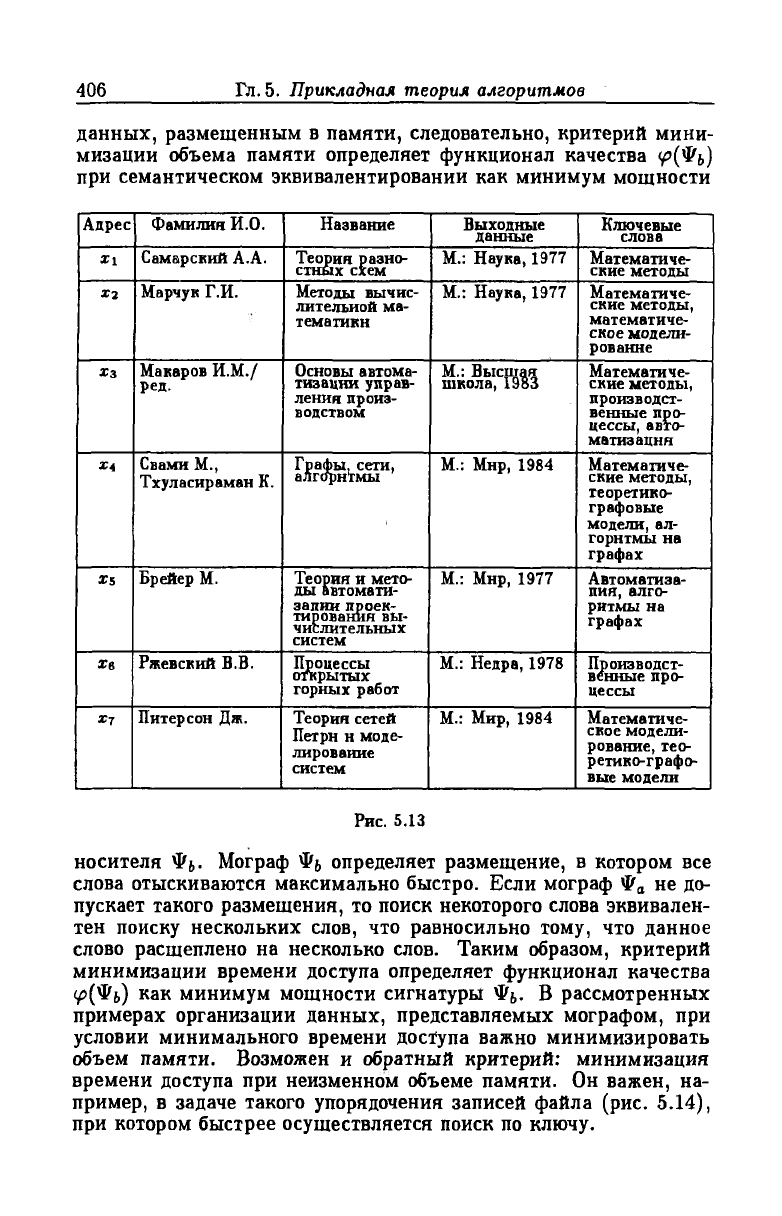
Рассмотрим файл библиотечной информационной системы (рис. 5.13). Он

имеет несколько ключей доступа: по фамилии автора, по названию издатель

ства, по ключевому слову и др. Для ускорения доступа файл можно упорядочить

по одному из ключей (обычно по фамилии), по другим же ключам записи будут

совершенно неупорядочены. В рассматриваемом примере индекс по ключу до

ступа “ключевое слово” представляется уже приведенным ранее мографом (см.

рис. 5.12,в), слову Mi соответствует значение “математические методы”, слову

Мг — “автоматизация” и т. д.

Мограф может задавать не только инвертированные списки, но и другие

списковые организации индексов: мультисписки, секционные списки. Наконец,

просто двоичная матрица может рассматриваться как матрица инцидентностей

мографа.

Основными критериями при размещении данных в памяти

ЭВМ являются минимизация объема памяти и времени доступа.

Элементы носителя мографа однозначно соответствуют объектам

406

Гл. 5. Прикладная теория алгоритмов

данных, размешенным в памяти, следовательно, критерий мини

мизации объема памяти определяет функционал качества <р(Фь)

при семантическом эквивалентировании как минимум мощности

Адрес

Фамилия И.О.

Название

Выходные

данные

Ключевые

слова

XI Самарский А.А. Теория разно

стных схем

М.: Наука, 1977

Математиче

ские методы

Марчук Г.И. Методы вычис

лительной ма

тематики

М.: Наука, 1977

Математиче

ские методы,

математиче

ское модели

рование

Макаров И.М./

ред.

Основы автома

тизации управ

ления произ

водством

М.: Высшая

школа, 1983

Математиче

ские методы,

производст

венные про

цессы, авто

матизация

Свами М.,

Тхуласираман К.

Графы, сети,

алгоритмы

М.: Мнр, 1984

Математиче

ские методы,

теоретико

графовые

модели, ал

горитмы на

графах

Брейер М.

Теория и мето

ды автомати

зации проек

тирования вы

числительных

систем

М.: Мнр, 1977

Автоматиза

ция, алго

ритмы на

графах

Хв

Ржевский В.В.

Процессы

открытых

горных работ

М.: Недра, 1978 Производст

венные про

цессы

Х7

Питерсон Дж.

Теория сетей

Петри и моде

лирование

систем

М.: Мир, 1984 Математиче

ское модели

рование, тео-

ретико-графо-

вые модели

Рис. 5.13

носителя Ф(,. Мограф Фь определяет размещение, в котором все

слова отыскиваются максимально быстро. Если мограф Фа не до

пускает такого размещения, то поиск некоторого слова эквивален

тен поиску нескольких слов, что равносильно тому, что данное

слово расщеплено на несколько слов. Таким образом, критерий

минимизации времени доступа определяет функционал качества

¥>(Ф(,) как минимум мощности сигнатуры Ф(,. В рассмотренных

примерах организации данных, представляемых мографом, при

условии минимального времени доступа важно минимизировать

объем памяти. Возможен и обратный критерий: минимизация

времени доступа при неизменном объеме памяти. Он важен, на

пример, в задаче такого упорядочения записей файла (рис. 5.14),

при котором быстрее осуществляется поиск по ключу.

§5.2. Методы оптимального размещения данных

407

Доступ к объектам данных осуществляется с помощью неко

торой стандартной процедуры поиска, реализующей переход от

одного элемента памяти к другому. Переход осуществляется одно

значно, поэтому эту процедуру поиска можно формализовать функ-

Коли-

*з

ха

хг

хп

Хб

Указа

тель

чество Ключевое слово

записей

Указа

тель

Коли

чество Ключевое слово

записей

Математические

методы

Автоматизация

Алгоритмы

на графах

Теоретико

графовые

модели

Математическое

моделирование

Производствен

ные процессы

Хб

хг_

s-*

Математические

методы

— •

2 Автоматизация

Алгоритмы

на графах

Теоретико

графовые

модели

— «

Математическое

моделирование

—

Производствен

ные процессы

Адрес Файл

i i

Самарский А.А.

х2

Марчук Г.И.

хз

Макаров И.М./

ред.

х*

Свами М.,

Тхуласираман К.

Х5

Брейер М.

Хв

Ржевский В.В.

Х7

Питерсон Дж.

цией осмотра памяти S — частичной функ

цией на множестве элементов носителя

мографа S: X —> X; S(x) — элемент, к

которому осуществляется переход после

элемента х. Рассмотрим такое размещение

данных и такую функцию осмотра памяти

S (модель Фь), при которых для каждого

слова М модели Фь имеется такой элемент

хо € М, что

М = {*0, S(x0), S2(x0), .. , S ^ -'ix о)},

Рис. 5.14

т. е. каждое слово отыскивается с помощью

функции S на основании только информа

ции о мощности слова и начальном элементе xq.

Подобные мографы называются допустимыми. Очевидно, что

на практике большинство мографов не являются допустимыми.

Для их реализации в памяти ЭВМ необходимо расщепление эле

ментов носителя или расщепление слов. При этом увеличивается

либо объем памяти, либо время доступа. Допустимые же мографы

представляются в памяти ЭВМ безызбыточным образом и требуют

минимального времени доступа.

Таким образом, задача оптимального размещения данных за

ключается в преобразовании мографа в допустимый и в построе

нии функции осмотра памяти. При этом функционалом качества

408

Гл. 5. Прикладная теория алгоритмов

является минимальное расширение носителя без изменения сиг

натуры или минимальное расширение сигнатуры без изменения

носителя. Эта задача имеет графовую интерпретацию. Рассмо

трим функцию осмотра памяти S: X —)• X допустимого мографа

Фь как отношение смежности S С X X X вершин в ориентирован

ном графе Gf = (X, S), построенном на множестве вершин X.

Граф G/ является функциональным (/-графом), т. е. из каждой

вершины его исходит не более одной дуги.

Теорема 5.2. Связный f -граф является либо ациклическим,

либо содержит точно один цикл.

Из этого утверждения следует, что практически важными яв

ляются следующие классы /-графов и допустимых мографов,

представляющихся соответствующими /-графами: линейные (пу

ти) , циклические (контуры), ациклические (ориентированные де

ревья). На практике функция осмотра памяти реализуется либо

с помощью указателей, либо переходом к соседнему элементу па

мяти. Для представления в памяти линейных графов можно ис

пользовать второй вариант реализации функции осмотра памяти.

Представление циклических /-графов также основано на переходе

к соседнему элементу памяти, но с одним исключением: S(xn) =

= Xi, где х\, хп — соответственно первый и последний в разме

щении элементы. Для представления ациклических /-графов необ

ходимы указатели. Однако представление ациклического /-графа

парами (x,S(х)) для каждой вер-

Г! 2 f t f t № 6 7 ^ ’ 1 И f t ^ 131 М ft^ М f t I ieff i9| fjao[

" I III !■■■■' —.111.1 I J >■ J

2I31

4Is 6

7 8 9

ieh9taql 16

Рис. 5.15

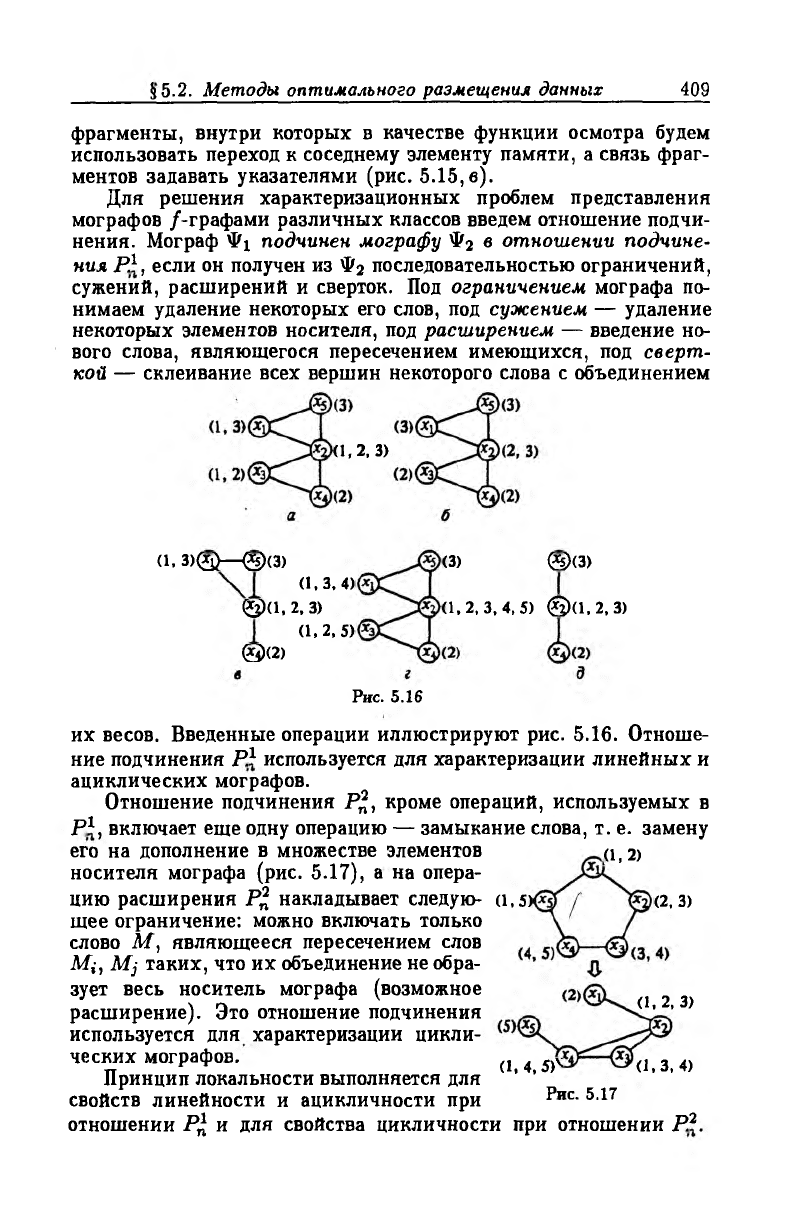
j; 5.2. Методы оптимального размещения данных

409

фрагменты, внутри которых в качестве функции осмотра будем

использовать переход к соседнему элементу памяти, а связь фраг

ментов задавать указателями (рис. 5.15,в).

Для решения характеризационных проблем представления

мографов /-графами различных классов введем отношение подчи

нения. Мограф Фх подчинен мографу Ф2 в отношении подчине

ния Р*, если он получен из Фг последовательностью ограничений,

сужений, расширений и сверток. Под ограничением мографа по

нимаем удаление некоторых его слов, под сужением — удаление

некоторых элементов носителя, под расширением — введение но

вого слова, являющегося пересечением имеющихся, под сверт

кой — склеивание всех вершин некоторого слова с объединением

(1,2.3)

(1.3)®)—©(3)

(1, 3. 4)

©(1, 2, 3)

(1, 2. 5)

& ( 2)

(3) ©(3)

.(1, 2)

(2. 3)

Р и с. 5.16

их весов. Введенные операции иллюстрируют рис. 5.16. Отноше

ние подчинения Р* используется для характеризации линейных и

ациклических мографов.

Отношение подчинения Р%, кроме операций, используемых в

Р*, включает еще одну операцию — замыкание слова, т. е. замену

его на дополнение в множестве элементов

носителя мографа (рис. 5.17), а на опера

цию расширения Р% накладывает следую- (1,5)

шее ограничение: можно включать только

слово М , являющееся пересечением слов

Mi, Mj таких, что их объединение не обра

зует весь носитель мографа (возможное

расширение). Это отношение подчинения

используется для характеризации цикли

ческих мографов.

Принцип локальности выполняется для

свойств линейности и ацикличности при

отношении Р£ и для свойства цикличности при отношении Р2.

(1, 4, 5)v

Рис. 5.17

(1, 2, 3)

(1, 3, 4)

410

Гл. 5. Прикладная теория алгоритмов

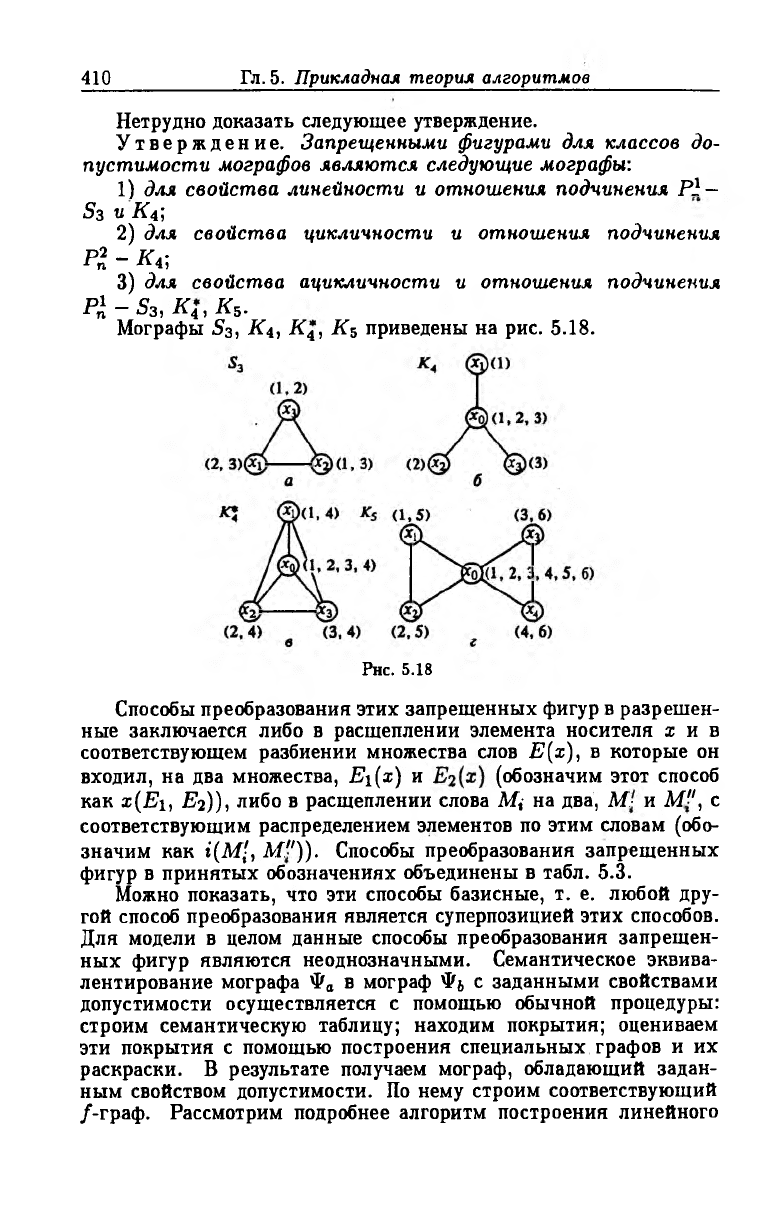
Нетрудно доказать следующее утверждение.

Утверждение. Запрещенными фигурами для классов до

пустимости мографов являются следующие мографы:

1) для свойства линейности и отношения подчинения Pi —

S3 и К4;

2) для свойства цикличности и отношения подчинения

П - Кг,

3) для свойства ацикличности и отношения подчинения

Рп1 - s3> К4 I КЪ.

Мографы S3, К4, К4, К$ приведены на рис. 5.18.

Рнс. 5.18

Способы преобразования этих запрещенных фигур в разрешен

ные заключается либо в расщеплении элемента носителя х и в

соответствующем разбиении множества слов Е(х), в которые он

входил, на два множества, Ei(x) и (обозначим этот способ

как х(Е\, Е2)), либо в расщеплении слова Af,- на два, М- и М", с

соответствующим распределением элементов по этим словам (обо

значим как i(M[, Af")). Способы преобразования запрещенных

фигур в принятых обозначениях объединены в табл. 5.3.

Можно показать, что эти способы базисные, т. е. любой дру

гой способ преобразования является суперпозицией этих способов.

Для модели в целом данные способы преобразования запрещен

ных фигур являются неоднозначными. Семантическое эквива-

лентирование мографа Фа в мограф Фь с заданными свойствами

допустимости осуществляется с помощью обычной процедуры:

строим семантическую таблицу; находим покрытия; оцениваем

эти покрытия с помощью построения специальных графов и их

раскраски. В результате получаем мограф, обладающий задан

ным свойством допустимости. По нему строим соответствующий

/-граф. Рассмотрим подробнее алгоритм построения линейного