Горбатов В.А. Фундаментальные Основы Дискретной Математики. Информационная Математика

Подождите немного. Документ загружается.

§4.10. Синтез нейронных структур 371

Первая реализация была предложена в виде гексагональной струк

туры (B.JI. Белявский, В.А. Горбатов, 1970 г.; рис. 4.79), где вес

синапса г-й переменной w(x{) определяется числом горизонталь

ных цепей, на вход которых подается переменная Х{. Каждая

горизонтальная цепь представляет собой последовательно включен-

Аксоны

Синапсы

Квизипороги

х>

-О - |

>Ключи

Рис. 4.79. Гексагональная структура нейрона

ные между собой ключи, при этом, если в рассматриваемой цепи

нечетные ключи открываются переменной Х{, а четные — пере

менной I,-, то в соседних горизонтальных цепях, наоборот, не

четные ключи открываются переменной х,, четные — переменной

Х{. Ключи, открывающиеся переменной ц, в дальнейшем будем

называть неинверсными, а открывающиеся переменной х; — ин

версными ключами.

Нейрон гексагональной структуры описывается булевой функ

цией вида

1, если 53 wi ' xi = Tj,

1=1

0 в противном случае,

где Tj — разрешенный квазипорог, а множество разрешенных

квазипорогов {Ту} моделирует порог Г в смысле У. Мак-Каллока и

У. Питтса.

Настройка нейрона на заданную булеву функцию f(xi, х2, ...

..£„) сводится к определению весов синапсов Wi и множества

<р(х 1, Х2, • . ., Хк) —

разрешенных квазипорогов Tj. Единичные точки ха булевой

функции/(xi, х2, ..., in)) f(xa) = 1, соответствуют разрешенным

квазипорогам Tj, нулевые точки хр, f(xp) = 0, — запрещенным

квазипорогам Ps.

Для определения {Гу} и {Р,} составляем две системы урав

нений: систему для определения множества разрешенных квази

порогов и систему для определения множества запрещенных ква

зипорогов. Системы решены, если любые два квазипорога Tj и

372

Гл. 4. Теория формальных грамматик и автоматов

Р3 не равны друг другу: (Vj, s) (Tj ф Ps). Тривиальное решение

получаем, если

= 2*-';

в этом случае значения Tj и Р, будут равны десятичному количе

ственному эквиваленту соответствующего двоичного набора. Оче

видно, что каждый вес синапса равен 1, если функция f(xi, х2,...

. . in) является симметрической.

Нетрудно показать, что функция f(x\, х2, ■.., хп) является

симметрической, если в соответствующем гиперкубе не найдется

яруса, который содержит хотя бы две точки, в которых эта функ

ция принимает различные значения. Обычно качество настройки

нейрона определяют значением суммы весов синапсов, т. е. при

настройке она минимизируется:

Для уменьшения трудоемкости настройки нейрона введем по

нятие графа неравенства GH = (Vw, U), каждой вершине которого

взаимно однозначно соответствует вес синапса и две вершины сое

динены ребром тогда и только тогда, когда соответствующие веса

синапсов представлены в виде одинаковых алгебраических сумм,

♦l(*l. х2’ *з>

входящих в различные системы уравнений: один вес — в сис

тему разрешенных квазипорогов, другой — в систему запрещен

ных квазипорогов.

Используя введенное понятие, рассмотрим синтез (настройку)

нейрона, реализующего булеву функцию

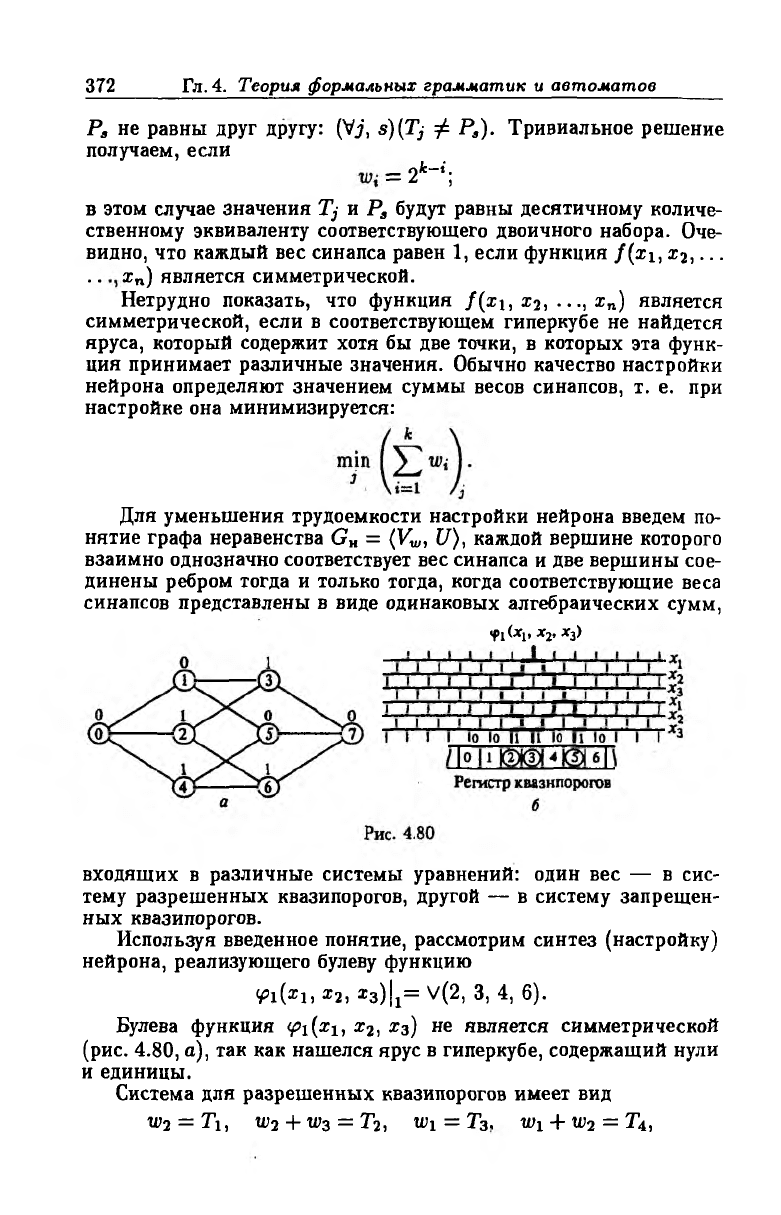
Vi(*i> *з> ®з)fi= V(2, 3, 4, 6).

Булева функция <fii(xi, х2, Хз) не является симметрической

(рис. 4.80, а), так как нашелся ярус в гиперкубе, содержащий нули

и единицы.

Система для разрешенных квазипорогов имеет вид

w2 = Ti, w2 + w3 = Т2, Wi = Т3, Wi + W

= TA,

§4.11. Моделирование автоматных систем сетями Петри 373

для запрещенных —

Р0 = 0 , W

= Pi, Wi + W

= Р2, W i+W 2 + W3 = Р3.

Анализ уравнений показывает, что граф неравенства весов яв

ляется полным, следовательно, веса синапсов попарно различны.

Пусть wi = 3, w2 = 2, w3 = 1; тогда

{T'} = {2,3,5}, {Pj} = { 1,4,6}.

Решение найдено, нейрон имеет вид, представленный на

рис. 4.80,5. На рис. 4.80, б в горизонтальной цепи перечеркнутый

ключ соответствует инверсному ключу, обведенный кругом номер

разряда регистра квазипорогов содержит 1, необведенный содер

жит 0 .

Содержимое регистра квазипорогов имеет вид .. .0011010...

§ 4.11. Моделирование автоматных систем сетями Петри

В связи со все более широким использованием параллельных

и распределенных вычислительных систем особую актуальность

приобретают дискретные структуры, представляющие параллель

ные процессы. Аппаратом описания сложных систем взаимодей

ствующих процессов являются формальные системы типа сетей

Петри, моделирующие динамические свойства систем.

Формализм сетей Петри общего вида основан на понятии ком

плекта, являющегося в некотором роде обобщением понятия мно

жества. Как и множество, комплект — это набор элементов, но

деяний элемент может входить в него более одного раза. Иначе

говоря, отношение включения, связывающее элементы и множе

ства, заменяются на функцию числа экземпляров элемента в ком

плекте, которая обозначается #(ж, В) (читается: число х в ком

плекте В). Множество — частный случай комплекта.

Многие понятия теории множеств распространяются и на ком

плекты. Так, пустой комплект аналогичен пустому множеству.

Мощность комплекта есть общее число экземпляров элементов

в комплекте. Комплект А включен в комплект В (является под-

комплектом), если для всякого х #(х, А) < #(*, В). С помощью

функции # легко определяются операции над комплектами:

объединение комплектов А и В

#(*, A U В) = шах (#(*, А), #(*, В));

пересечение комплектов А и В

#(х, АПВ) = min (#(х, А), #(*, В));

сумма комплектов А и В

#(*, А + В) = #(х, А) + #(х, В);

разность комплектов А и В

#(*, А -В )= # {х , А )-# (х , АП В).

374

Гл. 4. Теория формамных грамматик и автоматов

Если М — множество, то Мп — множество всех таких ком

плектов, построенных из элементов М, что #(х, В) < п, В € М п;

М°° — множество всех комплектов, построенных из элементов М

без ограничения на число экземпляров элемента в комплекте.

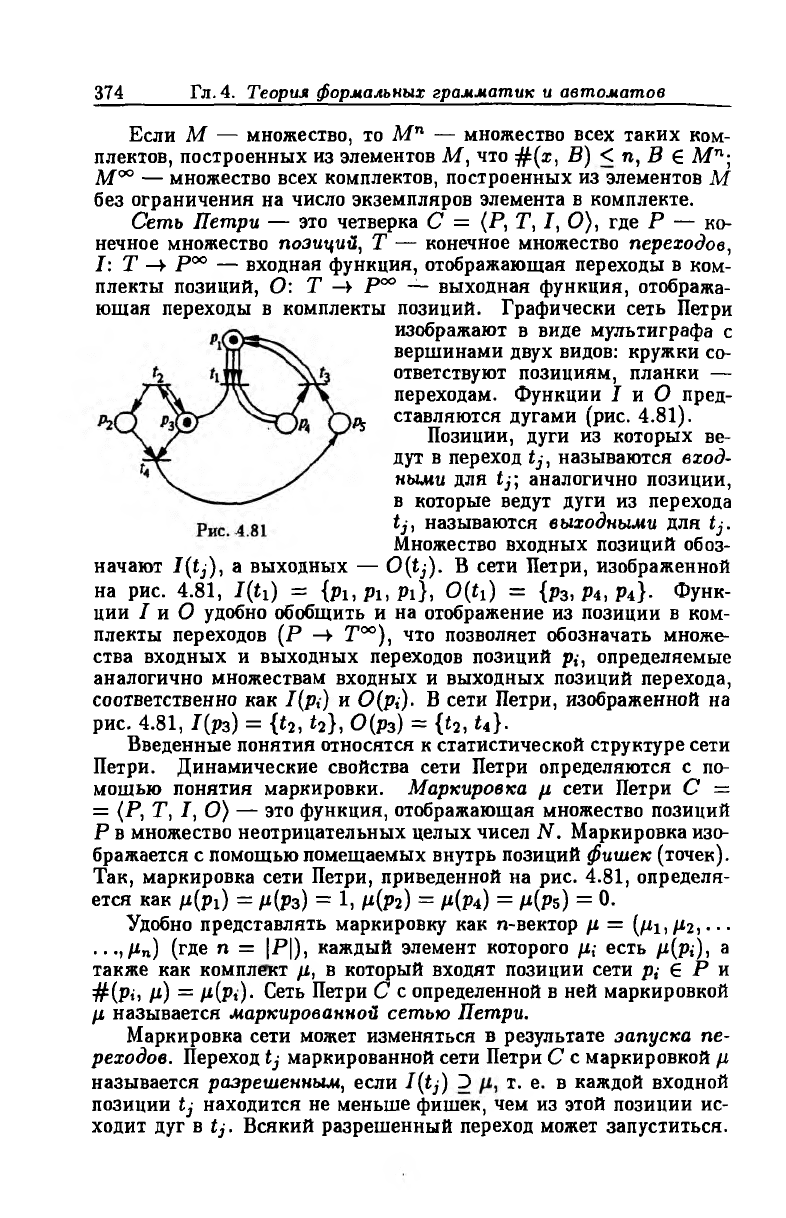
Сеть Петри — это четверка С = (Р, Т, I, О), где Р — ко

нечное множество позиций, Т — конечное множество переходов,

I: Т —У Р°° — входная функция, отображающая переходы в ком

плекты позиций, О: Т —► Р°° — выходная функция, отобража

ющая переходы в комплекты позиций. Графически сеть Петри

изображают в виде мультиграфа с

вершинами двух видов: кружки со

ответствуют позициям, планки —

переходам. Функции I и О пред-

^ ставляются дугами (рис. 4.81).

Позиции, дуги из которых ве

дут в переход tj, называются вход

ными для tj; аналогично позиции,

в которые ведут дуги из перехода

tj,

называются выходными для tj.

Множество входных позиций обоз

начают I(tj), а выходных — 0(tj). В сети Петри, изображенной

на рис. 4.81, 1(h) = {pi,pi,pi}, 0(h) = {рг,Р*,Р\}- Функ

ции I и О удобно обобщить и на отображение из позиции в ком

плекты переходов (Р —У Т°°), что позволяет обозначать множе

ства входных и выходных переходов позиций р,-, определяемые

аналогично множествам входных и выходных позиций перехода,

соответственно как 1(р,) и 0(pi). В сети Петри, изображенной на

рис. 4.81, 1(р3) = {*2, *г}, 0(рз) = {t2, М -

Введенные понятия относятся к статистической структуре сети

Петри. Динамические свойства сети Петри определяются с по

мощью понятия маркировки. Маркировка ц сети Петри С =

= (Р, Т, I, О) — это функция, отображающая множество позиций

Р в множество неотрицательных целых чисел N. Маркировка изо

бражается с помощью помещаемых внутрь позиций фишек (точек).

Так, маркировка сети Петри, приведенной на рис. 4.81, определя

ется как fi(pi) = /х(р3) = 1, ц(р2) = /х(р4) = /х(Р5) = 0.

Удобно представлять маркировку как n-вектор /х = (fii, ц2,...

...,fin) (где п = |Р|), каждый элемент которого /х,- есть /х(р;), а

также как комплект ц, в который входят позиции сети р,- ё Р и

#(Pi, fj) = A4(Р*)■ Сеть Петри С с определенной в ней маркировкой

р. называется маркированной сетью Петри.

Маркировка сети может изменяться в результате запуска пе

реходов. Переход tj маркированной сети Петри С с маркировкой ц

называется разрешенным, если /(fj) Э т- е- в каждой входной

позиции tj находится не меньше фишек, чем из этой позиции ис

ходит дуг в tj. Всякий разрешенный переход может запуститься.

§4.11. Моделирование автоматных систем сетями Петри 375

В результате запуска перехода tj маркировка сети fi изменяется

на новую: fi' = fi — I(tj) + О (tj), т. е. из всякой входной позиции

Pi перехода £,• удаляется столько фишек, сколько дуг ведет из р%

в tj, а в каждую выходную позицию pt помещается столько фи

шек, сколько дуг ведет из tj в рк. Последовательность запусков

переходов называется выполнением сети Петри.

Рассмотрим выполнение сети Петри, изображенной иа рис. 4.81. В началь

ной маркировке разрешен только переход t?. При его запуске фишка удалится

т рз, а затем в позиции рз и рз добавится по фишке, т. е. в результате запуска

щ новой маркировке fi' появится фишка еще и в р?. Теперь становятся разре

шенными переходы Ьз, U- Поскольку запуститься может любой разрешенный

переход, предположим, что запускается переход f<. После его запуска из позиций

рз н рз фишки удаляются, а в позиции ps появится одна фишка. В получив

шейся маркировке ц" не разрешен ни один переход. На этом выполнение сети

• Петри заканчивается.

Рассмотрим маркировку ц сети Петри С = (Р, Т, I, О). Мар

кировка fi1 называется непосредственно достижимой из fi, если

Найдется такой переход tj G Т, разрешенный в fi, что при его

запуске получается маркировка и'; в этом случае пара (fi, fi') при

надлежит отношению непосредственной достижимости, опре

деленному на Р°°. Транзитивное замыкание этого отношения на

зывается отношением достижимости. Маркировки fi' такие,

что пара (fi, fi') принадлежит отношению достижимости, назы

ваются достижимыми из fi. Множество достижимых из fi мар

кировок сети Петри С называется множеством достижимости

и обозначается R(C, fi).

Интерпретация сетей Петри основана на понятиях условия и

события. Состояние системы описывается совокупностью усло

вий. Функционирование системы состоит в осуществлении после

довательности определенных действий, т. е. событий. Для воз

никновения события необходимо выполнение некоторых условий,

называемых предусловиями. Возникновение события может при

вести к нарушению предусловий и к выполнению некоторых дру

гих условий, называемых

постусловиями. В сети Петри условия

Моделируются позициями, события — переходами. Предусловия

события представляются входными позициями соответствующего

перехода, постусловия — выходными позициями. Возникновение

События моделируется запуском перехода. Выполнение условий

представляется наличием фишек в соответствующих позициях, не

выполнение — их отсутствием.

Рассмотрим, например, простую вычислительную систему, по

следовательно обрабатывающую задания, которые поступают во

Входную очередь.

Когда процессор свободен и во входной очереди имеется за

дание, оно обрабатывается процессором, затем выводится. Эту

систему можно промоделировать сетью Петри, изображенной на

рис. 4.82.

376

Гл. 4. Теория формальных грамматик и автоматов

Установим, какие особенности систем учитывают сети Петри.

Это прежде всего асинхронностпъ. В сети Петри отсутствует поня

тие времени. Время возникновения событий никак не указыва

ется, но тем не менее структура сети Петри устанавливает частич

ный порядок возникновения событий. Далее, поскольку возник

новение событий представляется запуском переходов, предполага

ется, что события происходят мгновенно. Если же моделируемое

событие имеет отличную от нуля длительность, как, например, со

бытие “задание обрабатывается” (рис. 4.82), и это существенно,

то оно представляется в виде двух мгновенных событий типа “на

чало события”, “конец события” и условия “событие происходит”

(рис. 4.83). Кроме того, считается, что события происходят неод

новременно. Действительно, если допустить одновременное воз

никновение некоторых событий * и j, которым в сети Петри соот

ветствуют переходы £,• и tj, то можно вести дополнительный пе

реход^- с I(tij) = I(ti)+I(tj), 0(tij) = 0(ti)+ 0(tj), интерпрети

рующийся как одновременное

возникновение событий г и j.

В этом случае переходы можно

запускать последовательно.

Задание помещается

во входную очередь

Задание

обрабатывается

Вывод

задания

Задание ждет

уч Процессор

свободен

Задание ждет

вывода

Задание

х. обрабатывается

Начало Завершение

выполнения

задания

выполнения

задания

Рис. 4.82 Рис. 4.83

Другим важным свойством сетей Петри как инструмента моде

лирования является их способность представлять параллелизм и

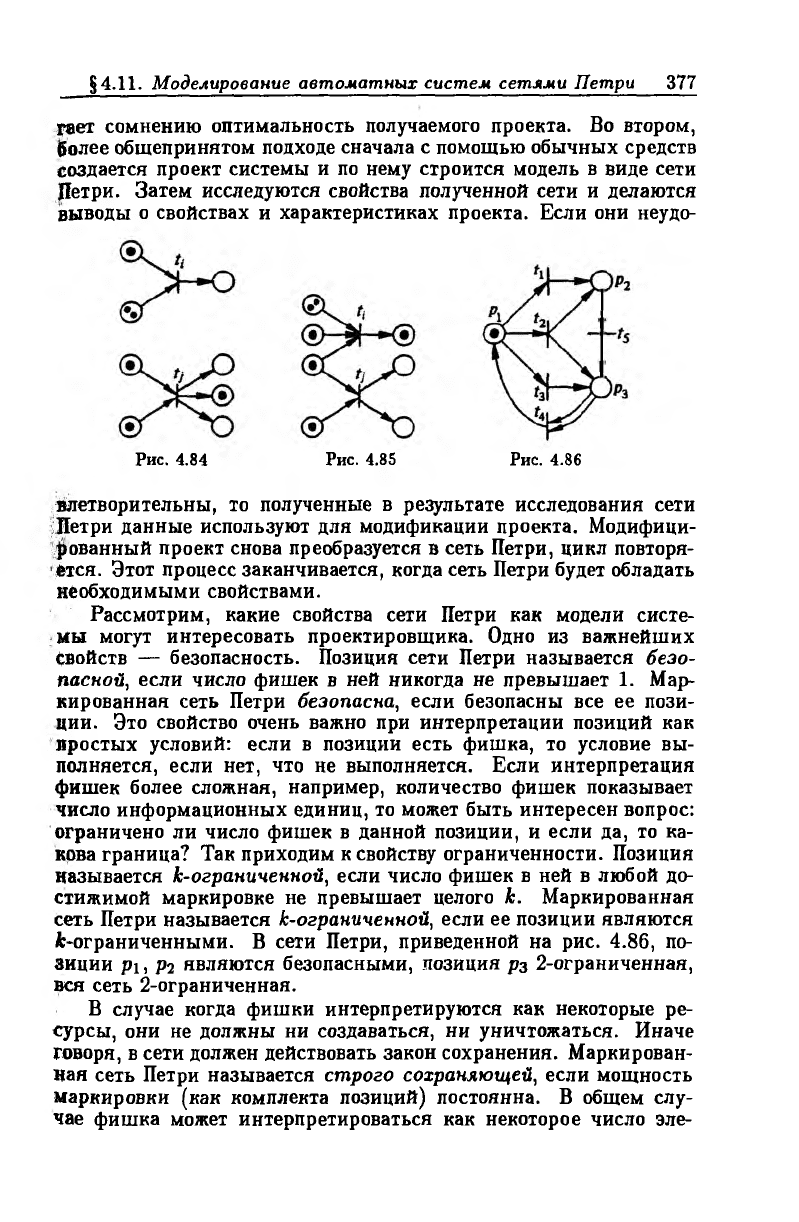
конфликтные ситуации. Параллелизм двух событий представля

ется двумя разрешенными переходами, множества входных пози

ций которых не пересекаются (рис. 4.84), конфликт — переходами

с общей входной позицией (рис. 4.85).

Сети Петри используют в основном как формальный аппарат

при моделировании систем, которым присущ параллелизм. Если

рассматривать процесс проектирования в целом, то возможны два

принципиально различных подхода к использованию сетей Петри.

В первом система моделируется сетью Петри, которая преобразу

ется по определенным правилам к некоторому “оптимальному”

виду. Полученная сеть Петри преобразуется в проект системы.

Предполагается, что он также оптимальный. Здесь сети Петри

применяют непосредственно при проектировании. Этот подход,

однако, имеет 1рудности, связанные с неоднозначностью обрат

ного преобразования (сети Петри в проект системы), что подвер-

§4.11. Моделирование автоматных систем сетями Петри 377

рвет сомнению оптимальность получаемого проекта. Во втором,

более общепринятом подходе сначала с помощью обычных средств

создается проект системы и по нему строится модель в виде сети

Детри. Затем исследуются свойства полученной сети и делаются

выводы о свойствах и характеристиках проекта. Если они неудо

влетворительны, то полученные в результате исследования сети

Петри данные используют для модификации проекта. Модифици

рованный проект снова преобразуется в сеть Петри, цикл повторя

ется. Этот процесс заканчивается, когда сеть Петри будет обладать

необходимыми свойствами.

Рассмотрим, какие свойства сети Петри как модели систе

мы могут интересовать проектировщика. Одно из важнейших

Свойств — безопасность. Позиция сети Петри называется безо

пасной, если число фишек в ней никогда не превышает 1. Мар

кированная сеть Петри безопасна, если безопасны все ее пози

ции. Это свойство очень важно при интерпретации позиций как

простых условий: если в позиции есть фишка, то условие вы

полняется, если нет, что не выполняется. Если интерпретация

фишек более сложная, например, количество фишек показывает

число информационных единиц, то может быть интересен вопрос:

ограничено ли число фишек в данной позиции, и если да, то ка

кова граница? Так приходим к свойству ограниченности. Позиция

называется к-ограниченной, если число фишек в ней в любой до

стижимой маркировке не превышает целого к. Маркированная

сеть Петри называется к-ограниченной, если ее позиции являются

fc-ограниченными. В сети Петри, приведенной на рис. 4.86, по

зиции pi, Р2 являются безопасными, позиция рз 2-ограниченная,

вся сеть 2-ограниченная.

В случае когда фишки интерпретируются как некоторые ре

сурсы, они не должны ни создаваться, ни уничтожаться. Иначе

Говоря, в сети должен действовать закон сохранения. Маркирован

ная сеть Петри называется строго сохраняющей, если мощность

маркировки (как комплекта позиций) постоянна. В общем слу

чае фишка может интерпретироваться как некоторое число эле

Рис. 4.84

Рис. 4.85

Рис. 4.86

378

______

Гл. 4. Теория формальных грамматик и автоматов

ментарных ресурсов, причем это число меняется от позиции к

позиции. Введем понятие взвешивания позиций: вектор W =

= (wi, w2, ..., w„), где Wi — вес позиции pi. Сеть Петри назы

вается сохраняющей по отношению к вектору взвешивания W ,

если скалярное произведение вектора W и маркировки (рассма

триваемой как вектор) постоянно; сеть Петри сохраняющая, если

она является сохраняющей по отношению к вектору взвешивания

W, все элементы которого положительны.

Рассмотренные до сих пор свойства относятся как к последо

вательным, так и к параллельным системам. Но при переходе от

последовательных систем к параллельным возникают принципи

ально новые трудности: возможность тупиковых ситуаций. Ту

пиком в сети Петри называется множество переходов, которые в

некоторой достижимой маркировке /х' и в последующих достижи

мых из /х' маркировках не разрешены. Свойство возможности

возникновения тупиков в системе моделируется свойством актив

ности в сетях Петри. Переход tj называется активным, если он не

входит ни в какой тупик. Переход называется пассивным, если он

не разрешен ни в какой достижимой маркировке. При детальном

исследовании активности сети Петри используют также понятие

уровней активности.

Переход tj обладает активностью:

уровня 0, если он не может быть запущен (пассивный);

уровня 1, если он потенциально запустим, т. е. существует

достижимая маркировка, в которой он разрешен;

уровня 2, если для любого целого к существует последователь

ность запусков переходов, в которой он присутствует не менее к

раз;

уровня 3, если существует бесконечная последовательность за

пусков, в которой он присутствует неограниченно часто;

уровня 4, если он потенциально запустим из всякой достижи

мой маркировки (т. е. активен).

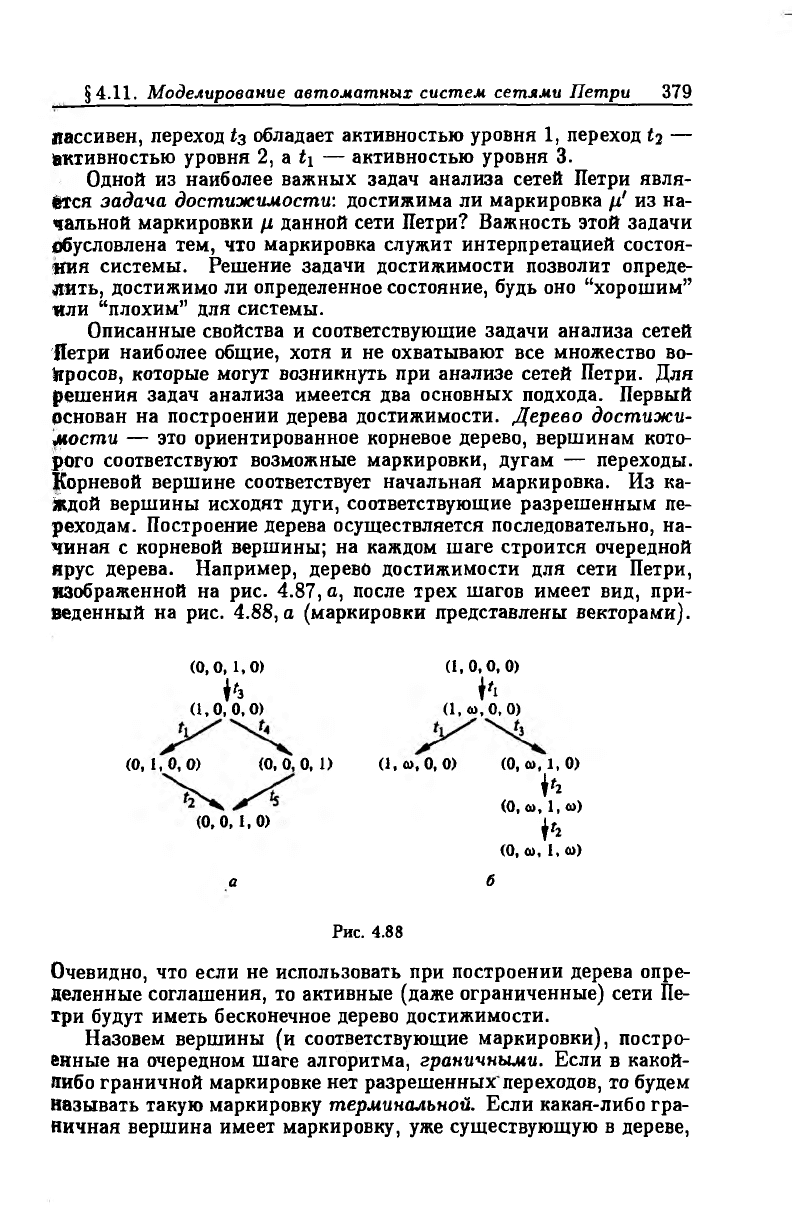
В сети Петри, изображенной на рис. 4.87, а, переход t3 активен,

переходы t\, t2, й, *6 имеют уровень активности 3; переход t$

пассивен. В сети Петри, приведенной на рис. 4.87, б, переход £4

§4.11. Моделирование автоматных систем сетями Петри 379

пассивен, переход^ обладает активностью уровня 1, переход ^ —

(активностью уровня 2, a ti — активностью уровня 3.

Одной из наиболее важных задач анализа сетей Петри явля

ется задача достижимости: достижима ли маркировка /х' из на

чальной маркировки /х данной сети Петри? Важность этой задачи

обусловлена тем, что маркировка служит интерпретацией состоя

ния системы. Решение задачи достижимости позволит опреде

лить, достижимо ли определенное состояние, будь оно “хорошим”

или “плохим” для системы.

Описанные свойства и соответствующие задачи анализа сетей

Петри наиболее общие, хотя и не охватывают все множество во

просов, которые могут возникнуть при анализе сетей Петри. Для

решения задач анализа имеется два основных подхода. Первый

основан на построении дерева достижимости. Дерево достижи

мости — это ориентированное корневое дерево, вершинам кото

рого соответствуют возможные маркировки, дугам — переходы.

Корневой вершине соответствует начальная маркировка. Из ка

ждой вершины исходят дуги, соответствующие разрешенным пе

реходам. Построение дерева осуществляется последовательно, на

чиная с корневой вершины; на каждом шаге строится очередной

ярус дерева. Например, дерево достижимости для сети Петри,

изображенной на рис. 4.87, а, после трех шагов имеет вид, при

веденный на рис. 4.88, а (маркировки представлены векторами).

(0, 0, 1, 0) (1, 0, 0, 0)

f a fa

(1,0, 0.0) (1.0), 0,0)

(1,о>, 0, 0) (0, <о,1.0)

(О, О), 1, со)

(О, а), 1, ш)

Рис. 4.88

Очевидно, что если не использовать при построении дерева опре-

деленные соглашения, то активные (даже ограниченные) сети Пе-

три будут иметь бесконечное дерево достижимости.

Назовем вершины (и соответствующие маркировки), постро

енные на очередном шаге алгоритма, граничными. Если в какой-

яибо граничной маркировке нет разрешенных переходов, то будем

называть такую маркировку терминальной. Если какая-либо гра

ничная вершина имеет маркировку, уже существующую в дереве,

(О, 1,0,0) (0,0,0, 1)

(0,0,1,0)

380

Гл. 4. Теория формальных грамматик и автоматов

то назовем ее дублирующей. Для терминальных и дублирующих

вершин не будем строить исходящих из них дуг. Это обеспечивает

конечность дерева достижимости для ограниченной сети Петри

(рис. 4.87, а, 4.88, а). Для неограниченных сетей требуется как-то

обозначить неограниченное число фишек в позиции. Пусть и обо

значает такое число, причем и + а — w, и — а = и, а < и>, ш < и>,

где о — произвольное целое положительное число. Будем исполь

зовать при построении дерева достижимости следующее правило.

Пусть граничная вершина ц ие является терминальной или ду

блирующей. Для каждого разрешенного перехода tj в маркировке

ц построим дугу, исходящую из ц. Дугу будем помечать перехо

дом tj. Маркировка р! новой вершины определяется следующим

образом. Если /х(р,) = ш, то /х'(р,) = и. Если на пути от корневой

вершины к /х существует вершина fi" такая, что в результате за

пуска в ц перехода tj число фишек в каждой позиции не меньше,

чем в fi", а в позиции р,- строго больше, то /*'(р,) = и. В противном

случае ft1 (pi) — число фишек в позиции р,-, получающееся после

запуска tj из ц (рис. 4.88, б).

Теорема 4.6. Дерево достижимости любой сети Петри

конечно.

Доказательство этого утверждения основано на свойствах ш и

на правилах введения этого символа в маркировку граничных вер

шин.

Метод анализа, основанный на дереве достижимости, позво

ляет определить свойства безопасности, ограниченности, сохране

ния, исследовать свойства активности и достижимости.

Сеть Петри ограничена тогда и только тогда, когда символ из от

сутствует в дереве достижимости. Кроме того, положение символа

ш показывает, какие позиции неограничены. Если символ и> отсут

ствует в дереве, то число достижимых маркировок конечно, и все

вопросы анализа можно решить простым перебором. В частности,

для нахождения границы маркировки данной позиции р,- нужно

найти наибольшее значение *-й компоненты среди всех вершин

дерева. Если эта граница не превышает 1, то позиция безопасная.

Для установления того, является ли сеть Петри сохраняющей

по отношению к некоторому вектору взвешивания W = (u>i,

к?2, ..., wn), необходимо решить следующую систему линейных

уравнений с ограничениями:

£ ™«Mi(P.) = s при j - 1, • • к,

<=1

Wi > 0 при г = 1, ..., п,

где к — число вершин дерева достижимости, которым соответ

ствуют различные маркировки. (Очевидно, что если имеется

fij(pi) = и, то Wi = 0.)