Горбатов В.А. Фундаментальные Основы Дискретной Математики. Информационная Математика
Подождите немного. Документ загружается.


§ 4.9. Синтез логических структур в связных базисах
_____
361
В рассмотренном в этом параграфе примере не учитывалось
распределение красок в структурном графе H(f), так как допуска
лось парафазное представление входной информации. Читателю
предлагается опустить это ограничение и построить абсолютно ми
нимальные логические схемы в рассматриваемых пяти базисах с
учетом распределения красок в структурном графе H(f), как это
делалось в конце предыдущего параграфа.
§ 4.9. Синтез логических структур в связных базисах
В общем виде решение системы связных структурных уравне
ний (4.26) является открытой проблемой при поиске минималь
ных логических структур. Рассмотрим приближенное решение
этой проблемы.
Число направлений, на которое разлагается структурный граф
при преобразовании его в функциональный, равно числу входных
каналов базисного элемента. В зависимости от выбранных на
правлений при выполнении операции разложения получаем раз
личные сложности функционального графа. Если преобразуемый
структурный граф H(f) имеет 7V_ (Л/_ > kBX) максимальных
вершин, то для получения функционального графа минимальной
сложности необходимо произвести (j^“) различных разложений и
каждое из них оценить.
Для оценки разложений будем использовать топологические
характеристики структурных графов H(f) и Н(Ь). Сравнение
топологических характеристик этих графов дает возможность оп
ределять оптимальное разложение структурных графов, что осо
бенно важно при проектировании логических схем в многофунк
циональных базисах, т. е. базисах, содержащих многофункцио
нальные модули — модули, на которых выделена группа входных
каналов, в зависимости от настройки которых выполняется та или
иная булева функция.
В качестве топологических характеристик будем рассматри
вать: v — цикломатическое число; I — длину графа (максималь
ную длину пути, содержащегося в графе); р — число путей; С —
П
связность, С = 1/n Yh Si, где s; — степень г-й вершины, п — чи-
i=i
ело вершин, т — число дуг; а — число максимальных элементов;
/3 — число минимальных элементов.
Оптимальное разложение структурного графа H(f) оценива
ется минимальным значением одного из функционалов
<рг[Н}, Н5) = ((v(Hj) - v(Hj))2 + (/(#/) - l{Hj))2 +
+ (p{Hj) - p(Hj))2 + (C(Hf) - С{Щ))2 + (n(Hf) - n(Hj))2 +
+ (m(Hf ) - m(Hj))2 + Qa(Hf) - /3(Hf)\ - )a(Hs) - 0(Hj)|)2)0,5, ,

362
Гл. 4. Теория формальных грамматик и автоматов
М И ,, Щ = res + res Ш + res Й- Ш +
I г с С(ВД I I r e ’" ™ | г а И " / )- е т \
C(Hj) » (Я,-) m № )+ |o(H ,)-/S(H ,)|’
где индексы / о т н о с я т с я к реализуемой функции, а индексы
j — к выбранному разложению (настройке многофункционального
модуля), res — остаток от целочисленного деления.
Функционал Hj) применяется, когда среднее значение
отклонения их топологических характеристик не превышает 2,
т. е. первый функционал используется при малом различии их
топологических характеристик, в противном случае применяется
второй функционал ip2(Н/, Hj).
В качестве иллюстрации введенных функционалов рассмотрим
проектирование логической схемы, реализующей булеву функцию
f(x 1, х2, х$, £4)|i = V(0, 1, 2, 7, 15), на элементах УСЭППА.
Структурный граф Н (/) имеет следующий вид:
H(f) = *2 , о{Щ, i 4)), 1г(х2, хг , Я4)).
Структурный граф Н(Ь), соответствующий элементу УСЭППА,
имеет матрицу соединений S = [stJ] вида
0
0
0 0 0 0 0 0
-1
0
0
0 0 0 0
0
-1 0
0
0
0 0
0
0
0
-1
0 0 0 0 0 0
0
-1
1 0
0 0 0 0
0
0
-1
0 0 0
0
0
0 0
0
0
1
0 0
0
0
0
0 0
-1
0
0
0
Матрица соединений является двухвходовой матрицей, каждой
строке (столбцу) которой взаимно однозначно соответствует вер
шина структурного графа Н = (F, 17), и
- - 1.
1, если (vj, Vj) £ U и эта дуга не перечеркнута,
(и<. vi)
если G U и эта дуга перечеркнута,
т. е. она является инверсной,
О, если («j, и3) ^ U.
Структурные графы Н\н Н2, соответствующие двум направле
ниям разложения, имеют соответственно вид:
Hi = n(zi, a(z2, I3)), H2 = n(z2, z3, z4).
В данном случае применим функционал <p\(Hj, Hj):
М Н ^Н г), М Н а,Н2), <pi(Hp, Hi), <pi(Hp, H2),

§ 4.9. Синтез логических структур в связных базисах 363
На = 7г(х х , Х2, <т(ж3) Х4)), Нр = п(х2, Х3, Х4).
Каждое из вычисленных значений функционала характеризует
близость соответствующих структурных графов
<pi(Ha, Hi) = ((0 - О)2 + (3 - 2)2 + (2 - 2)2 + 2 +
+ (4 - З)2 + (3 - 2)2 + (|1 - 2| - |2 - 1|)2)0,5 « v/ Щ .
Аналогично вычисляем
<pi(На, Hi) » \/4,04, <fi(Hp, Hi) = л/3, <pi(Hp, Н2) = 0.
Согласно вычисленным значениям <pi(Hf, Hj) структурный
граф Яа разлагаем по Hi, Нр— по Я 2. В результате получаем
структурно декомпозицию вида
H(f) = h(n(xi, х2), х4, х3, х2),
где h — идентификатор структурного графа Н(Ъ), определяющего
элемент УСЭППА.
Действуя аналогично, для функции jt(xi, х2) окончательно
получаем оптимальную логическую схему, состоящую из двух эле
ментов УСЭППА при парафазном представлении входной инфор
мации:
H (f(x 1, Х2, Х3, Я4)) = М М 0 , ХЪ ! . * 2), * 4 , хз, х2).
Структурный граф, соответствующий входу базисного элемен
та, с точностью до применения операции инверсии является под
графом структурного графа, соответствующего выходу этого же
базисного элемента. Отсюда можно предложить следующий ме
тод преобразования структурного графа в функциональный при
синтезе в связных базисах.
Для каждого элемента 6; связного базиса перечисляем различ
ные режимы Rj его работы и соответствующие им графы Hbt] ■
Режимы получают путем объединения входов элемента 6, и пу
тем подачи на вход констант, если такая возможность имеется.
Оцениваем графы Нь,} по числу вершин и согласно этой оценке
упорядочиваем их в порядке убывания этих чисел.
Выбираем первый граф Hi этого ряда и определяем, является
ли преобразуемый структурный граф Я/ суперпозицией согласно
Hi своих подграфов или их инверсий Нах, Яа2, ..., Накях- Если
является, то подграфы Я а1, Я а2, ..., Haktx являются искомыми
на этом шаге преобразования. Если нет, то выбираем второй граф
Я 2 этого ряда и повторяем проверку и т. д. до получения функцио
нального графа.
Оптимизацию этого процесса можно проводить, оценивая уда
ленность Я/ от Hi (Hai, Haj, . • Накях), г = 1, 2, ..., по их
топологическим характеристикам.
364 Гл. 4. Теория формальных грамматик и автоматов
Проиллюстрируем этот метод логических схем на элементах
УСЭППА.
Пусть необходимо синтезировать логическую схему на элемен
тах УСЭППА, реализующую булеву функцию вида
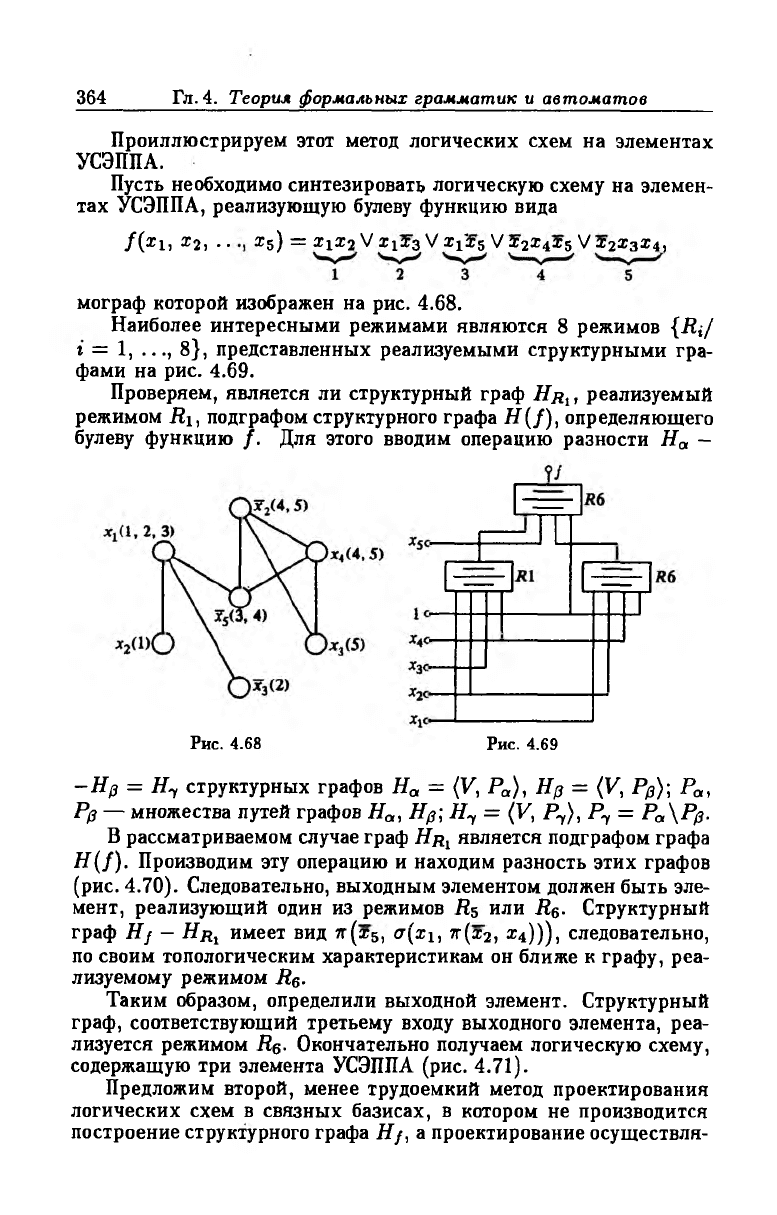
f(x 1, *2, . . * 5) = Z1Z2 V Х113 V х{х$ V х2х4хъ Vх2х3х4,
мограф которой изображен на рис. 4.68.
Наиболее интересными режимами являются 8 режимов {Ri/
г = 1, ..., 8}, представленных реализуемыми структурными гра
фами на рис. 4.69.
Проверяем, является ли структурный граф Яд^ реализуемый
режимом Ri, подграфом структурного графа Я (/), определяющего
булеву функцию /. Для этого вводим операцию разности На —
Рис. 4.68 Рис. 4.69
-Н (3 = Щ структурных графов На = (V, Ра), Нр = (V, Р0)\ Ра,
Рр — множества путей графов Яа , Н$\ Щ = (V, Ру), Ру = Ра \Рр.
В рассматриваемом случае граф Нцх является подграфом графа
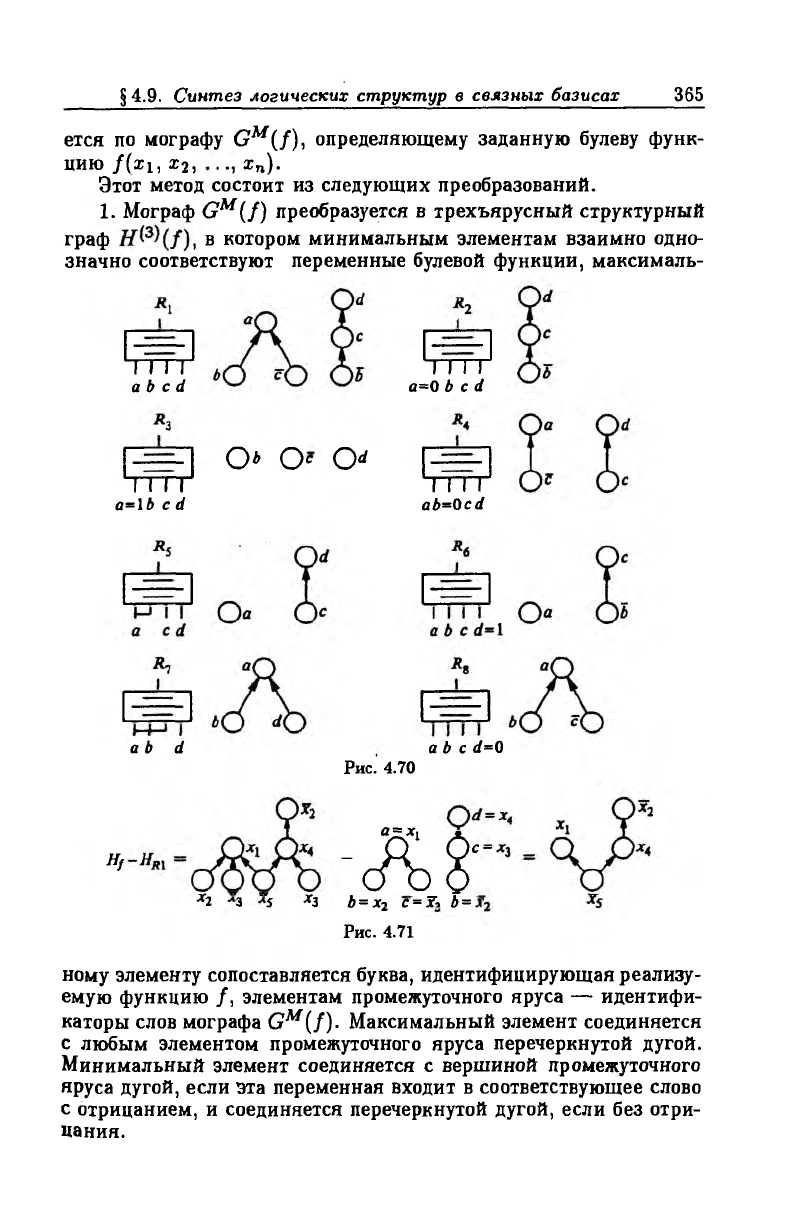
Я(/). Производим эту операцию и находим разность этих графов
(рис. 4.70). Следовательно, выходным элементом должен быть эле
мент, реализующий один из режимов Rs или Д6. Структурный
граф Hj — Hrx имеет вид 7г(х5, <7(2:1, ^(^2, £4))), следовательно,
по своим топологическим характеристикам он ближе к графу, реа
лизуемому режимом Re.
Таким образом, определили выходной элемент. Структурный
граф, соответствующий третьему входу выходного элемента, реа
лизуется режимом Re- Окончательно получаем логическую схему,
содержащую три элемента УСЭППА (рис. 4.71).
Предложим второй, менее трудоемкий метод проектирования
логических схем в связных базисах, в котором не производится
построение структурного графа Я/, а проектирование осуществля
§ 4.9. Синтез логических структур в связных базисах
_____
365
ется по мографу GM(f), определяющему заданную булеву функ
цию f(x 1, Х2, !„ ) .
Этот метод состоит из следующих преобразований.
1. Мограф GM(f) преобразуется в трехъярусный структурный
граф в котором минимальным элементам взаимно одно
значно соответствуют переменные булевой функции, максималь-
ТТТТ
abed
M il
e=0 bed
ГТТТ
а=\Ь с d
Q b Q c Q d
ГТТТ
ab=Ocd
a b d
Hf
a b с d=0
Рис. 4.70
-<K$'
x2 ”з *s *3 b = x2 с = ЪЬ = х
:*2
Рис. 4.71
ному элементу сопоставляется буква, идентифицирующая реализу
емую функцию /, элементам промежуточного яруса — идентифи
каторы слов мографа GM(f). Максимальный элемент соединяется
с любым элементом промежуточного яруса перечеркнутой дугой.
Минимальный элемент соединяется с вершиной промежуточного
яруса дугой, если эта переменная входит в соответствующее слово
с отрицанием, и соединяется перечеркнутой дугой, если без отри
цания.
366
Гл. 4. Теория формальных грамматик и автоматов
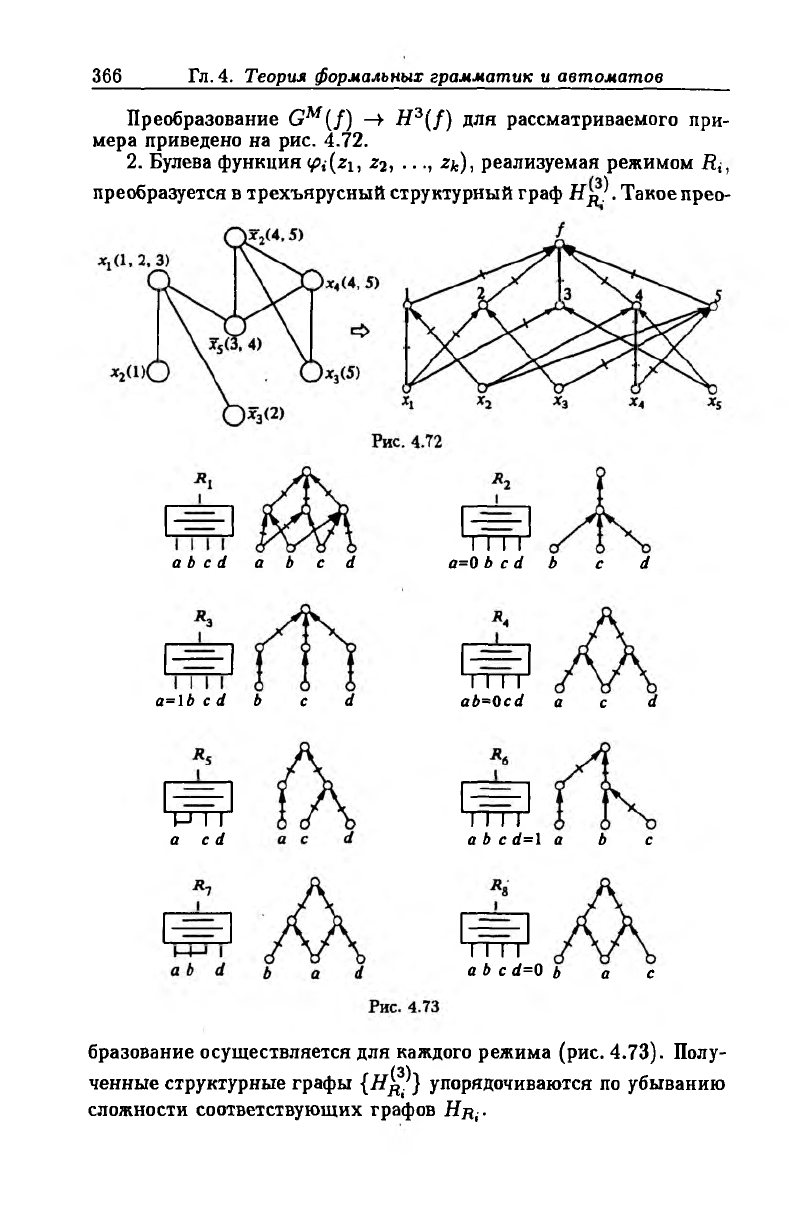
Преобразование GM(f) —V Я 3(/) для рассматриваемого при
мера приведено на рис. 4.72.
2. Булева функция <Pi(z\, z2, ..., z*), реализуемая режимом Ru
преобразуется в трехъярусный структурный граф Нд ?. Такое прео-
а Ь с d а Ь с d
I I I I
а=О Ь с d b с d
a=lb с d b с d
ГТТТ
ab=Ocd а с d
*РТТ
а с d
ТГГТ
а Ь с d=1 а Ь с
Т Т Л
а b с d=0 ь
а с
бразование осуществляется для каждого режима (рис. 4.73). Полу
ченные структурные графы {Н ^} упорядочиваются по убыванию
сложности соответствующих графов Нщ-

§ 4.9. Синтез логических структур в связных базисах 367
3. Определяется в порядке упорядочения, произведенного в п. 2,
содержится ли граф Яд} в качестве подграфа в Я(3)(/). Если да,
то путем, состоящим из*двух перечеркнутых дуг, выход элемента,
реализующего этот режим, соединяется с максимальной верши
ной графа H^\f) с одновременным вычитанием графа Нр^ из
Ж 3>(/).
Если ни одни из графов {Яне содержится в то
применением схемной алгебры Ас = (Н(3\ U, ), изоморфной ал
гебре множеств Ак = (М, U, ), граф (/) приводится к виду,
при котором он содержит один из графов {Яд3^}.
Схемной алгеброй Ас называется совокупность
(Ж 3), и, ">,
где носитель Я^3) — множество трехъярусных структурных гра
фов; сигнатура: U — объединение трехъярусных структурных
графов Я<3) U H f = Н?\ Я '3) = (V, Ра), H f = (V, Рр)-, Ра,
Рр — множества путей графов Н^\ Н^\ Н ^ = (V, Р7), Р7 =
= Ра U Рр] — инверсия структурного графа.
Выразим через операции U и третью операцию — пересече
ние структурных графов Н ^ П Я ^ :
В силу изоморфизма этой алгебры и алгебры множеств сигна
тура алгебры Ас удовлетворяет следующим законам:
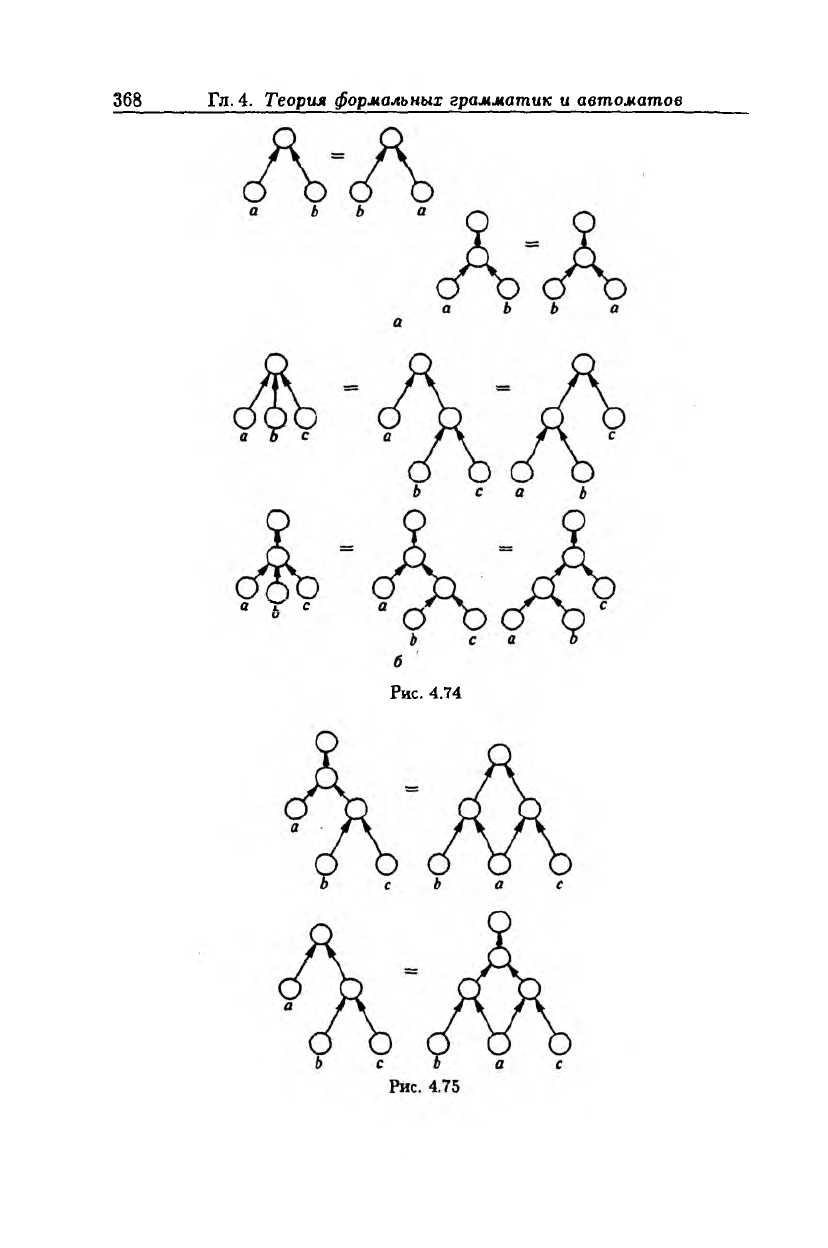
1) коммутативности объединения и пересечения (рис. 4.74, а)
aUb = bU а, а П Ь = Ь П а;
2) ассоциативности объединения и пересечения (рис. 4.74, б)
a U b U с = a U (6 U с) = (a U b) U с,
а П Ь П с = а П (Ь П с) = (а П Ь) П с;
3) дистрибутивности пересечения относительно объединения и
объединения относительно пересечения (рис. 4.75)
а П (b U с) = (а П b) U (а П с),
aU (ЬПс) = (а U 6) П (а U с);
4) идемпотентности объединения и пересечения (рис. 4.76, а)
aUa = a, аПа = а;
5) законам действия с константами (рис. 4.76, б)
a U 0 = a, a U 1 = 1, aUa = 1,
а П 0 = 0, а П1 = а, а П а = 0;
368
______
Гл. 4. Теория формальных грамматик и автоматов
а 'Г с
Рис. 4.74
§4.9. Синтез логических структур в связных базисах 369
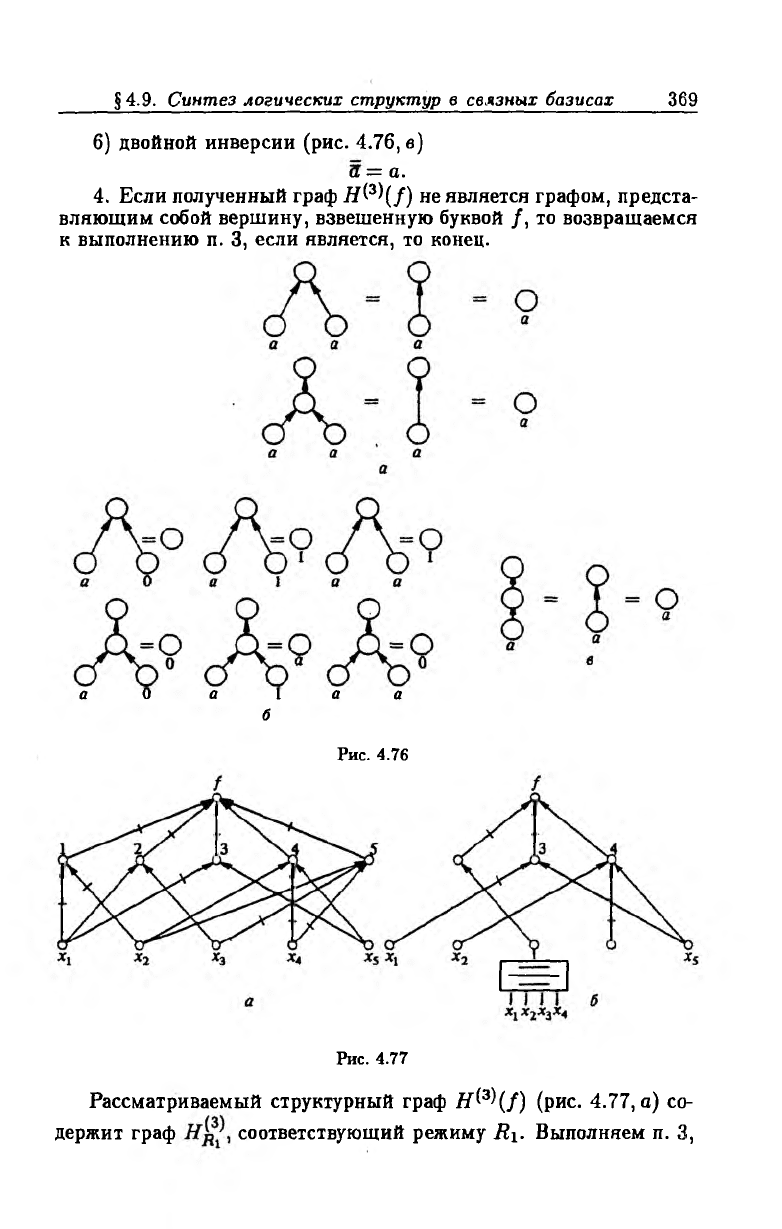
6) двойной инверсии (рис. 4.76, е)
а = а.
4. Если полученный граф Я(3)(/) не является графом, предста
вляющим собой вершину, взвешенную буквой /, то возвращаемся
к выполнению п. 3, если является, то конец.
а 0 а 1 а а
б
Рис. 4.76
Рис. 4.77
Рассматриваемый структурный граф H^z\f) (рис. 4.77, а) со
держит граф соответствующий режиму R\. Выполняем п. 3,
370
Гл. 4. Теория формальных грамматик и автоматов
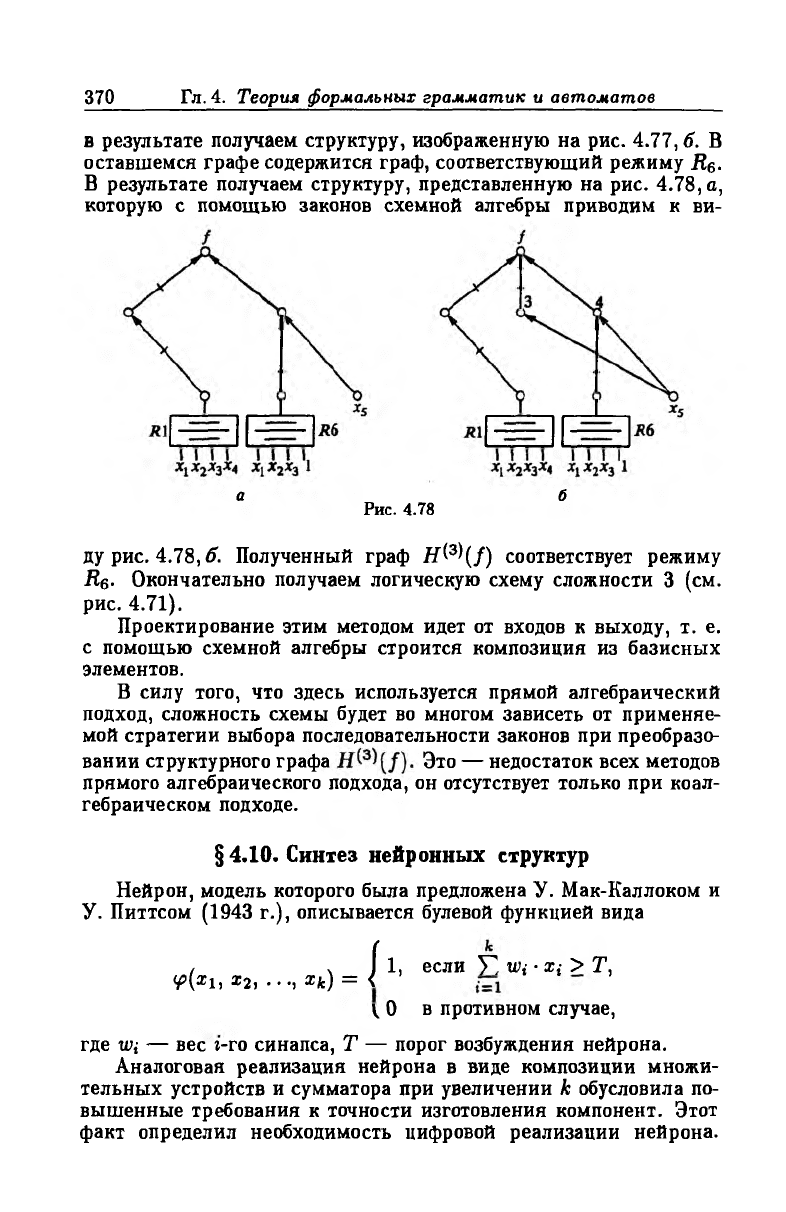
в результате получаем структуру, изображенную на рис. 4.77, б. В
оставшемся графе содержится граф, соответствующий режиму R6.
В результате получаем структуру, представленную на рис. 4.78, а,
которую с помощью законов схемной алгебры приводим к ви-
а б
Рис. 4.78
ду рис. 4.78, б. Полученный граф H^\f) соответствует режиму
Re- Окончательно получаем логическую схему сложности 3 (см.
рис. 4.71).
Проектирование этим методом идет от входов к выходу, т. е.
с помощью схемной алгебры строится композиция из базисных
элементов.
В силу того, что здесь используется прямой алгебраический
подход, сложность схемы будет во многом зависеть от применяе
мой стратегии выбора последовательности законов при преобразо
вании структурного графа Это — недостаток всех методов
прямого алгебраического подхода, он отсутствует только при коал-
гебраическом подходе.
§ 4.10. Синтез нейронных структур
Нейрон, модель которого была предложена У. Мак-Каллоком и
У. Питтсом (1943 г.), описывается булевой функцией вида
, V / 1, если у. Wi • Xi > Г,
<р(хи 1 2, .... Хк) = <
V 0 в противном случае,
где Wi — вес г-го синапса, Т — порог возбуждения нейрона.
Аналоговая реализация нейрона в виде композиции множи
тельных устройств и сумматора при увеличении к обусловила по
вышенные требования к точности изготовления компонент. Этот
факт определил необходимость цифровой реализации нейрона.
