Горбатов В.А. Фундаментальные Основы Дискретной Математики. Информационная Математика

Подождите немного. Документ загружается.

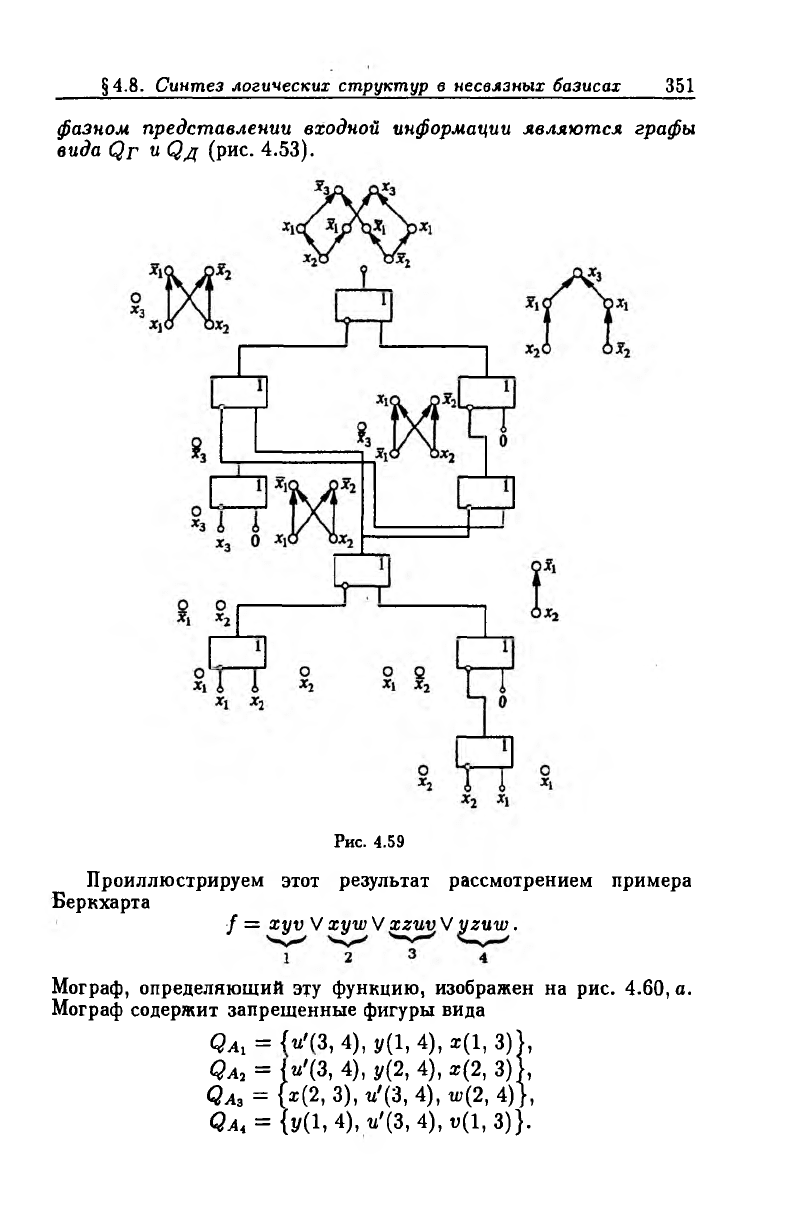
§4.8. Синтез логических структур в несвязных базисах 351

фазном представлении входной информации являются графы

вида Qp « <2д (рис. 4.53).

Рис. 4.59

Проиллюстрируем этот результат рассмотрением примера

Беркхарта

/ = xyvV xyw\/ xzuv\/ yzuw.

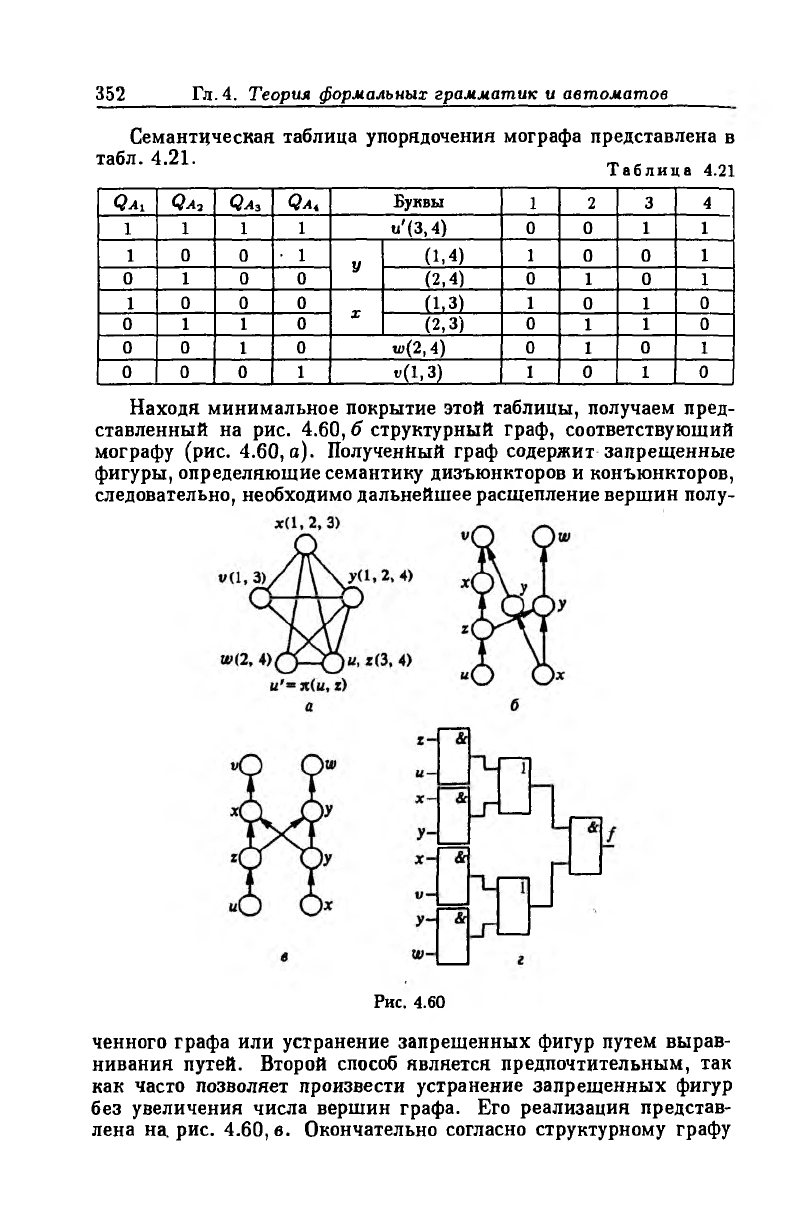
Мограф, определяющий эту функцию, изображен на рис. 4.60, а.

Мограф содержит запрещенные фигуры вида

Qai = М З , 4), у(1, 4), *(1, 3)|,

Qa2 = M 3, 4), 2/(2, 4), *(2, 3)},

Qa3 = {*(2, 3), щ'(3, 4), w(2, 4)},

Qa< = Ь (1, 4), «'(3, 4), и(1, 3)}.

352

Гл. 4. Теория формальных грамматик и автоматов

Семантическая таблица упорядочения мографа представлена в

табл. 4.21. ,

Таблица 4.21

Qai

Qa3

Qa<

Буквы

2 3 4

1 1

«'(3,4)

0 0

1 1

1 0

• 1

(1,4)

0 0

0 (2,4) 0

0 1

1 0

(1.3)

0 1 1

0 (2,3) 0

1 0

0 1

u>(2,4) 0 1 0 1

0 1

«(1,3)

1 0 1 0

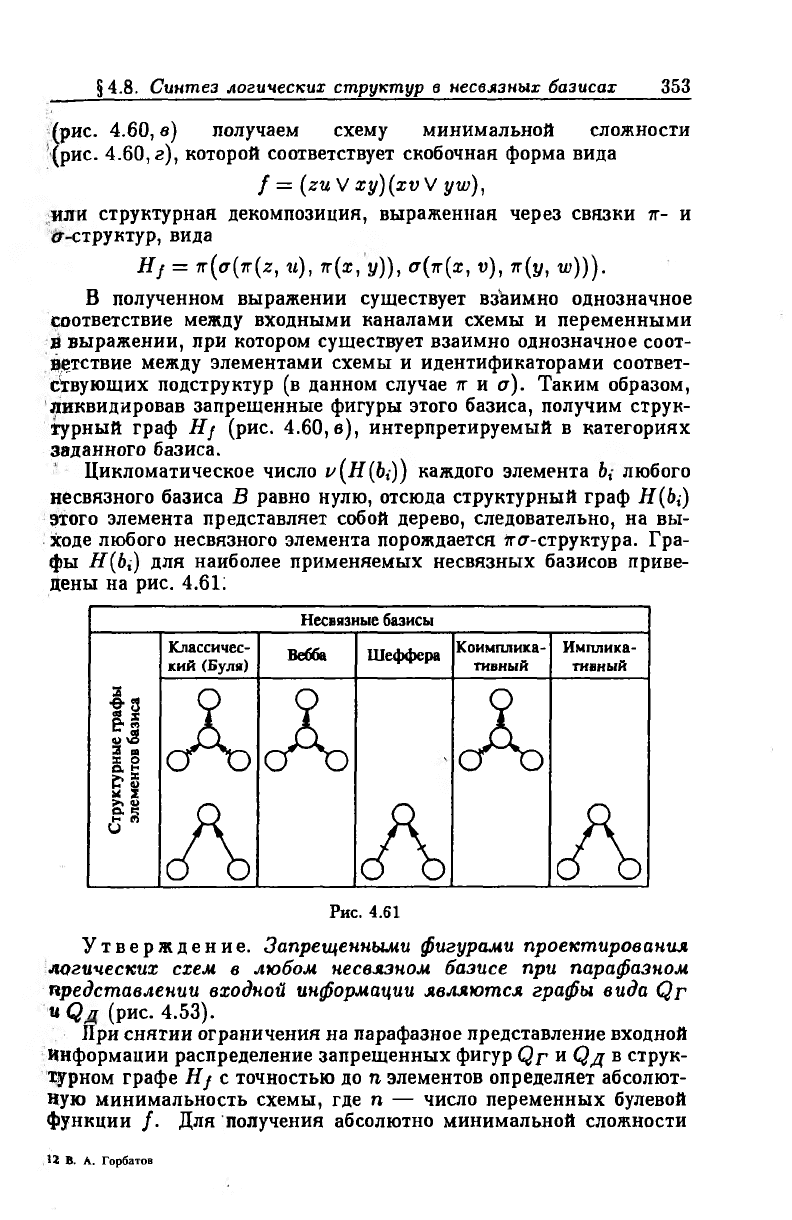
Находя минимальное покрытие этой таблицы, получаем пред

ставленный на рис. 4.60, б структурный граф, соответствующий

мографу (рис. 4.60, о). Полученйый граф содержит запрещенные

фигуры, определяющие семантику дизъюнкторов и конъюнкторов,

следовательно, необходимо дальнейшее расщепление вершин полу-

Рис. 4.60

ченного графа или устранение запрещенных фигур путем вырав

нивания путей. Второй способ является предпочтительным, так

как часто позволяет произвести устранение запрещенных фигур

без увеличения числа вершин графа. Его реализация представ

лена на, рис. 4.60, в. Окончательно согласно структурному графу

§4.8. Синтез логических структур в несвязных базисах 353

(рис. 4.60, в) получаем схему минимальной сложности

(рис. 4.60,г), которой соответствует скобочная форма вида

/ = (zuV ху) (xv V yw),

или структурная декомпозиция, выраженная через связки тг- и

а структур, вида

Я/ = 7t(ct(tt(z, ti), тг(х, у)), а(тг(х, и), тг(у, ш))).

В полученном выражении существует взаимно однозначное

соответствие между входными каналами схемы и переменными

Я выражении, при котором существует взаимно однозначное соот

ветствие между элементами схемы и идентификаторами соответ

ствующих подструктур (в данном случае тг и а). Таким образом,

ликвидировав запрещенные фигуры этого базиса, получим струк

турный граф Hj (рис. 4.60, в), интерпретируемый в категориях

заданного базиса.

Цикломатическое число 1/(Я(Ь,)) каждого элемента 6, любого

несвязного базиса В равно нулю, отсюда структурный граф Н(Ь{)

Этого элемента представляет собой дерево, следовательно, на вы

воде любого несвязного элемента порождается тгст-структура. Гра

фы Я(6,) для наиболее применяемых несвязных базисов приве

дены на рис. 4.61:

Несвязные базисы

Структурные графы

элементов базиса

Классичес

кий (Буля)

Вебба

Шеффера

Коимплика-

тивный

Имплика-

тивный

сДо

Рис. 4.61

Утверждение. Запрещенными фигурами проектирования

логических схем в любом несвязном базисе при парафазном

представлении входной информации являются графы вида Qp

tt Qn (рис. 4.53).

При снятии ограничения на парафазное представление входной

Информации распределение запрещенных фигур Qp и С}д в струк

турном графе Hj с точностью до тг элементов определяет абсолют

ную минимальность схемы, где п — число переменных булевой

функции /. Для получения абсолютно минимальной сложности

12 В. А. Горбатов

354 Гл. 4. Теория формальных грамматик и автоматов

логической схемы необходимо учитывать распределение перемен

ных ж,- и их отрицаний ж,- в структурном графе Я/.

Согласно весам ж,-, ж,- вершин структурного графа Я/ раскра

сим его вершины в два цвета (количество цветов равно значности

используемой логики): вершины, взвешенные переменными ж,-,

раскрасим в цвет а, вершины, взвешенные отрицаниями пере

менных ж,, — в цвет /?. Вершинам, раскрашенным цветом а, на

рисунках не будем приписывать штрихи, а вершинам, раскрашен

ным в цвет /?, будем приписывать.

Распределение весов ж,-, ж,- или раскраска структурного графа

в базисе называются разрешенными, если существует взаимно од

нозначное соответствие межу входными каналами и вершинами

графа Я/, при котором граф Я/ представим в виде бесповтор-

ной (с точностью до повтора одинаковых частей при одномерной

записи) структурной декомпозиции, связками которой являются

идентификаторы структурных графов базисных элементов. При

разрешенной раскраске на входе логической схемы не включено

ни одного инвертора. Разрешенная раскраска порождается путем

подстановки структурных графов, задающих базисные элементы

друг в друга.

Задача приведения заданной раскраски вершин графа Я/ к

разрешенной сводится к перекраске вершин, нарушающих раз

решенное распределение. Перекраска вершины и(ж^‘), ст,- = 0, 1,

означает появление на входе логической схемы инвертора, на вход

которого подается переменная ж,-.

Очевидно, что возможна перекраска не одной вершины, а сразу

всех вершин некоторого подграфа Я/(, Яд С Я/, что эквивалентно

включению инвертора внутри или на выходе схемы; при этом для

соблюдения эквивалентности реализуемой булевой функции / пе

рекрашиваемый подграф Я fi заменяется инверсным Я /,. Сле

довательно, для доказательства абсолютной минимальности спро

ектированной схемы необходимо осуществить возможную пере

краску подграфов Я/, заданного графа Я/.

Проиллюстрируем учет распределения весов ж,-, ж,- вершин

структурного графа Я/ проектированием логической схемы в ба

зисе Шеффера. Для определенности возьмем входной коэффици

ент квх (число входных каналов) базисного элемента, равный 2.

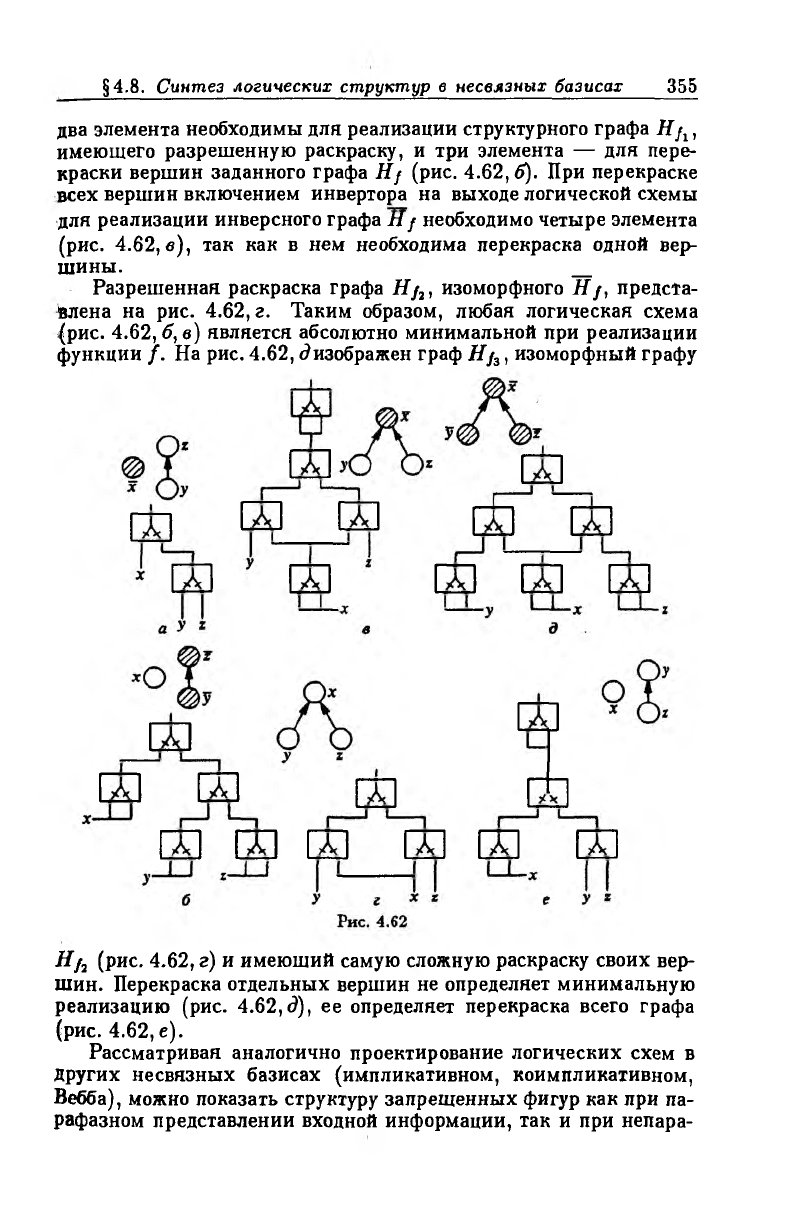
Пусть задана булева функция

/(ж, y,z) = ж V yz,

структурный граф Я/ которой представлен на рис. 4.62,5.

Разрешенной раскраской для изоморфных этому графу гра

фов является раскраска графа Я д, изображенного на рис. 4.62,а.

Сравнивая эти раскраски, замечаем, что для приведения раскраски

заданного графа к разрешенной необходима перекраска всех

трех вершин. Следовательно, сложность схемы будет равна 5:

§4.8. Синтез логических структур в несвязных базисах

355

два элемента необходимы для реализации структурного графа Я д ,

имеющего разрешенную раскраску, и три элемента — для пере

краски вершин заданного графа Я/ (рис. 4.62,6). При перекраске

всех вершин включением инвертора на выходе логической схемы

для реализации инверсного графа Я / необходимо четыре элемента

(рис. 4.62, в), так как в нем необходима перекраска одной вер

шины.

Разрешенная раскраска графа Я/2, изоморфного Я /, предста

влена на рис. 4.62, г. Таким образом, любая логическая схема

|рис. 4.62, б, в) является абсолютно минимальной при реализации

функции /. На рис. 4.62, «^изображен граф Я/3, изоморфный графу

Я/2 (рис. 4.62, г) и имеющий самую сложную раскраску своих вер

шин. Перекраска отдельных вершин не определяет минимальную

реализацию (рис. 4.62, д), ее определяет перекраска всего графа

(рис. 4.62, е).

Рассматривая аналогично проектирование логических схем в

Других несвязных базисах (импликативном, коимпликативном,

Вебба), можно показать структуру запрещенных фигур как при па-

рафазном представлении входной информации, так и при непара-

356

Гл. 4. Теория формальных грамматик и автоматов

фазном. Для определенности входной коэффициент квх функцио

нальных элементов возьмем равным 2.

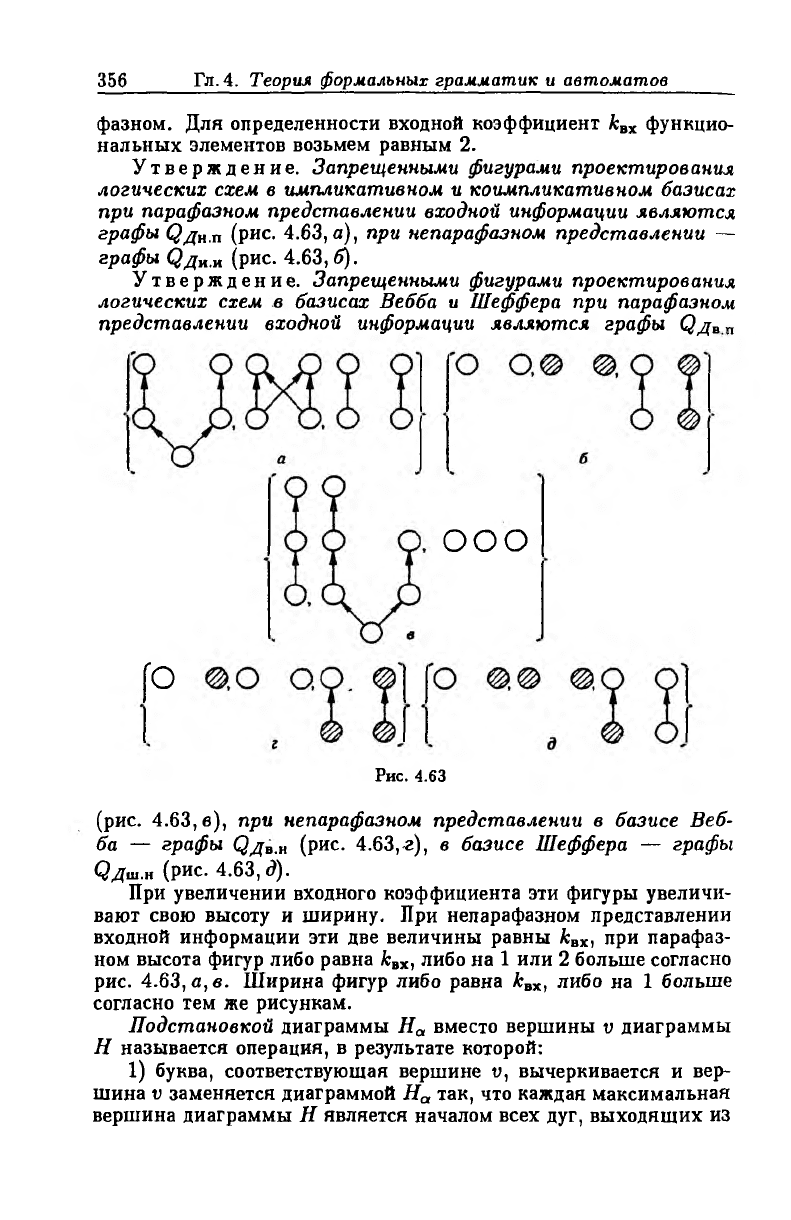
Утверждение. Запрещенными фигурами проектирования

логических схем в импликативном и коимпликативном базисах

при парафазном представлении входной информации являются

графы С}дн.п (рис. 4.63, а), при непарафаэном представлении —

графы фди.и (рис. 4.63,6).

Утверждение. Запрещенными фигурами проектирования

логических схем в базисах Вебба и Шеффера при парафазном

представлении входной информации являются графы С2д ВП

(рис. 4.63, в), при непарафаэном представлении в базисе Веб

ба — графы фдв.н (рис. 4.63,е), в базисе Шеффера — графы

Qдш.н (рис. 4.63, <?).

При увеличении входного коэффициента эти фигуры увеличи

вают свою высоту и ширину. При непарафаэном представлении

входной информации эти две величины равны А;вх, при парафаз

ном высота фигур либо равна квх, либо на 1 или 2 больше согласно

рис. 4.63, а, в. Ширина фигур либо равна Л;вх, либо на 1 больше

согласно тем же рисункам.

Подстановкой диаграммы На вместо вершины v диаграммы

Я называется операция, в результате которой:

1) буква, соответствующая вершине и, вычеркивается и вер

шина v заменяется диаграммой На так, что каждая максимальная

вершина диаграммы Я является началом всех дуг, выходящих из

ООО

Рис. 4.63

§4.8. Синтез логических структур в несвязных базисах 357

v, и каждая минимальная вершина Я является концом всех дуг,

входящих в вершину v;

2) если буква, соответствующая вершине, является инверсной,

то производится операция инверсии диаграммы х~(Н).

Операция, обратная подстановке, называется операцией свер

тывания диаграммы Я в вершину v.

Структурные графы Я/, не содержащие запрещенных фигур

Qjfи.п) Q^u.hj Q^B.m Q^b.hi Qmш.Н) при свертывании диаграмм,

соответствующих базисным элементам, свертываются в вершину,

взвешенную выходной буквой /. При этом существует взаимно

однозначное соответствие между буквами структурного графа Hj

и вхождением их в структурную декомпозицию с точностью до по

вторения общих частей.

В качестве упражнения читателю предлагается выделить за

прещенные фигуры <2д, фди.п, <2д я.н, <2дв.п, <2дв.н, <2дш.н и пре-

образовать структурный граф Я/ = (V(X), <):

F W = _

= {«(хХ), u(xi), v(x2), v(^2). V(S2),V(Z3), U(x3), u(®4), v(x4)},

l) < v(^2), v(Xi) < v(x4), vfx'J < v(x4),

v(x2l < v(xi) < v(x4}, v(%l) < и(*з),

v(x4) < u(x3), v(x4) < u(x3), v(x3) < v(x*4),

в минимальные логические схемы в базисах импликативном, ко-

импликативном, Вебба, Шеффера. Полученные результаты будут

иметь следующий вид:

Hf = hH(hK(hH(x3, hn(x4, 0)), hH(hH(hH(x4, 0), хз),

(Ли(хх, hK(x2, 0)))), hK{hK(hH{xi, hH(x2, 0)),

^и(^н(а;4| 0)i з-з))) hH(hH(hH(x2, 0), Xj), 0))),

Hf — Лк(1, hK(hK(hK(l, hK(hK(l, x2), ®i))j

^k(^k(^k(1| hK(X\, ^k(I) *2)))) ^4)1 ®з))|

Л-к(^к(Нк(х1, ^k(I) x2))> hK(hK(lt X4), X3)), hK(x3, hK(l, X4))))),

Hf — hB(hB(hB(hB(x3, hB(hB{x2, X4), hB(hB{x2, X2),

hB(x4, *4))))» hB(hB(x4, hB{x2> *2))»

ЬВ{хз, X3))), Xi), ^*b(^b(®2i Xi)), ^b(®3i X4))),

Hf = hui [hm (Ьш(Ьш(кш(х3, x3), Нш(х4, x4)), Лш(х3, x4)),

(*1. *a))), Л-ш (^Ш (^ш (^ш (^ш (^ш (хз, х3),

Лш(х4, х4))), Нш(х\, х2)), hjjj^hjjj^xi, Х\), hm{x2, 3-2)))))»

где Лй, hK, hB, hm — идентификаторы структурных графов Я(6),

соответствующих элементам в базисах импликативном, коимпли-

кативном, Вебба, Шеффера соответственно.

358

Гл. 4. Теория формальных грамматик и автоматов

Полученные структурные композиции определяют логические

схемы сложностью 13, 15, 16, 16.

Аналогично проектируются абсолютно минимальные логиче

ские схемы в любом несвязном базисе.

Характеризация семантики связных базисов в виде нахожде

ния запрещенных фигур проектирования логических схем в этих

базисах является открытой проблемой. Трудность заключается в

том, что для связных элементов необходимо согласовывать струк

турные графы, получающиеся внутри цикла графа, соответствую

щего базисному элементу. Это согласование учитывает вторую

группу уравнений в системе 4.26.

Точное проектирование логических схем в несвязных базисах

на основе их семантики заключается в реализации следующих

преобразований.

1. Синтезируется структурный граф Я(/), реализующий за

данную булеву функцию f(xi, х2, ..., хп).

2. Минимальным расширением носителя структурного графа

Я (/) с помощью покрытия семантической таблицы он приводится

к виду тгст-графов.

3. Определяются структурные графы Я(Ь^), соответствующие

элементам заданного базиса.

4. Начиная от выходного канала к входным структурный граф

Я (Л покрывается графами Я(Ь,).

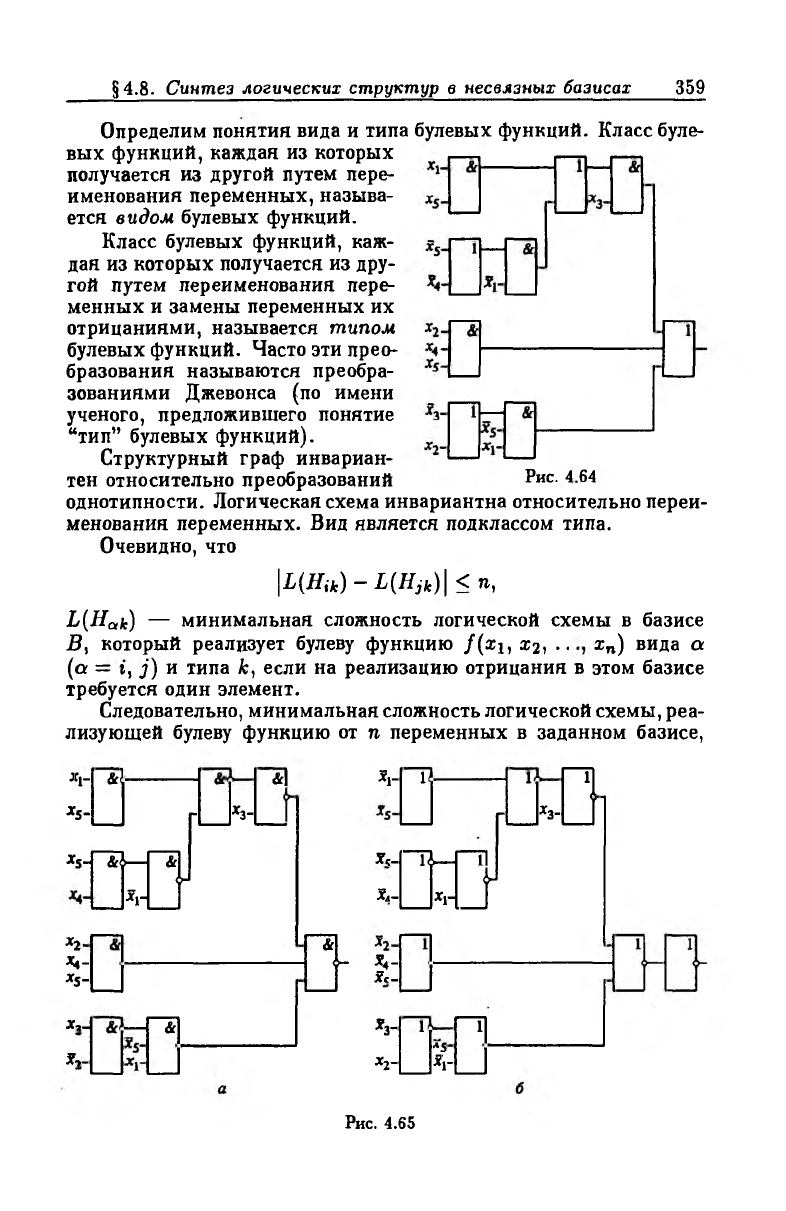
Проиллюстрируем эти преобразования проектированием логи

ческой схемы, реализующей булеву функцию

/(*1, *2, • • •, Хб) = Хгх2х5 V х{х3х5 V Z1Z3Z5 V

V Z1Z3Z4 V х1X3X5 V х2х4х5

в классическом базисе, базисах Шеффера, Вебба, импликативном

и коимпликативном с квх £ {2, 3}.

Выполнение пп. 1-3 было проведено выше (см. рис. 4.46, б,

4.54, 4.61). Рассмотрим реализацию п. 4. Преобразование в клас

сическом базисе осуществляется тривиальным образом. В полу

ченном согласно п. 2 выражении

Я (Л = а(тг(ж3, u(tt(zi, Х5), 7г(жх, и(®4, *5)))),

п(х2, Z4, Z5), *3), х[, *£))

связки тг и а заменяются соответственно на элементы к, и V

(рис. 4.64).

В других базисах при покрытии возможно появление согласую

щего элемента в каналах связи, работающего по схеме НЕ, когда

внешние связки базисного элемента не совпадают с внешней связ

кой непокрытого структурного графа Я(/). Результат покрытия

Я (/) графами Я(Ьх) в остальных базисах изображен на рис. 4.65-

4.67.

Проектирование осуществлено при допустимом парафазном

представлении входной информации.

§4.8- Синтез логических структур в несвязных базисах 359

Определим понятия вида и типа булевых функций. Класс буле

вых функций, каждая из которых

получается из другой путем пере

именования переменных, называ

ется видом булевых функций.

Класс булевых функций, каж

дая из которых получается из дру

гой путем переименования пере

менных и замены переменных их

отрицаниями, называется типом

булевых функций. Часто эти прео

бразования называются преобра

зованиями Джевонса (по имени

ученого, предложившего понятие

“тип” булевых функций).

Структурный граф инвариан

тен относительно преобразований Рис- 464

однотипности. Логическая схема инвариантна относительно переи

менования переменных. Вид является подклассом типа.

Очевидно, что

|L{Hik) - L(Hjk)\ < n,

L(Hak) — минимальная сложность логической схемы в базисе

В, который реализует булеву функцию f(x\, х2, • • хп) вида а

(а = t, j) и типа к, если на реализацию отрицания в этом базисе

требуется один элемент.

Следовательно, минимальная сложность логической схемы, реа

лизующей булеву функцию от п переменных в заданном базисе,

ЛЕ,-

&1 V

* 5-

хз-

*з-

*5-П^

*4-

X j-

Х,-|

*<-1

*л-

"11— П

_WJ

*>-

Хс-

*з-

*2-

л5

*i-

Рис. 4.65

360

______

Гл. 4. Теория формальных грамматик и автоматов

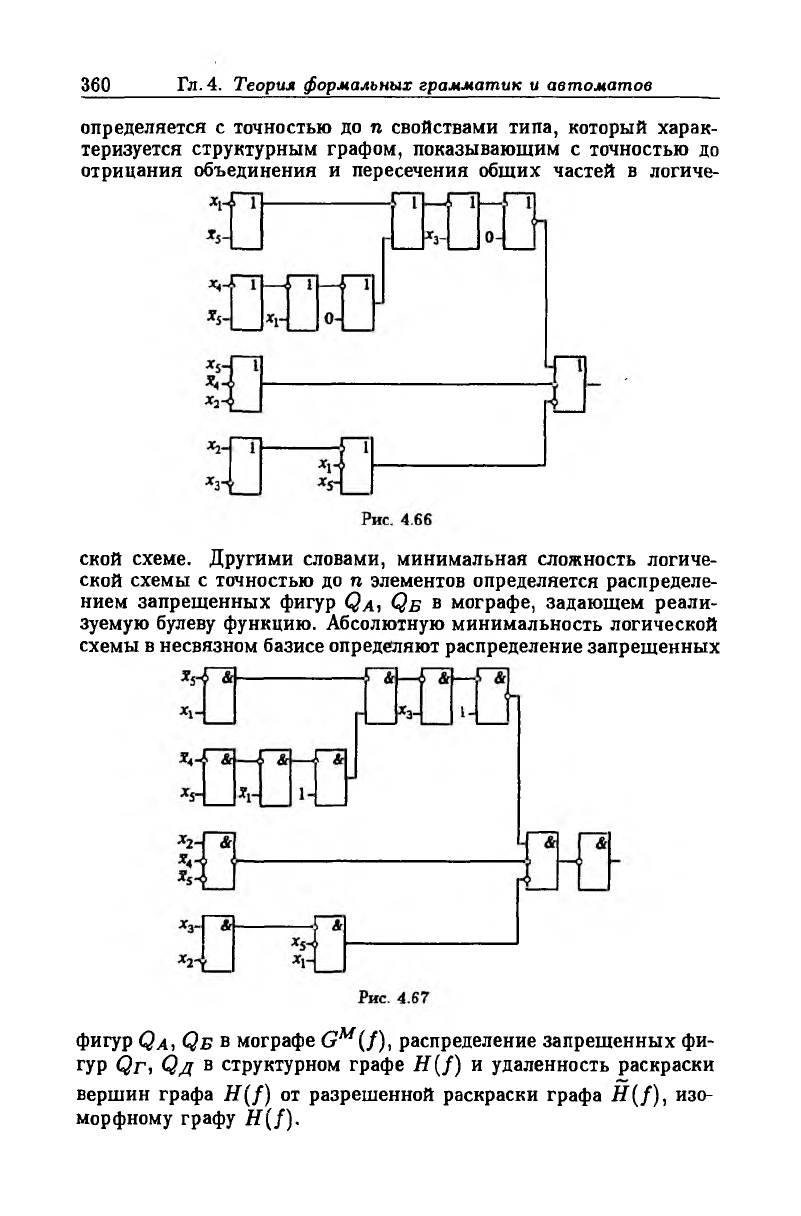
определяется с точностью до п свойствами типа, который харак

теризуется структурным графом, показывающим с точностью до

отрицания объединения и пересечения общих частей в логиче

ской схеме. Другими словами, минимальная сложность логиче

ской схемы с точностью до п элементов определяется распределе

нием запрещенных фигур Qa, Qb в мографе, задающем реали

зуемую булеву функцию. Абсолютную минимальность логической

схемы в несвязном базисе определяют распределение запрещенных

фигур Qa, Qb в мографе GM(f), распределение запрещенных фи-

гур Qr, Qm в структурном графе #(/) и удаленность раскраски

вершин графа #(/) от разрешенной раскраски графа #(/), изо

морфному графу H(f).