Горбатов В.А. Фундаментальные Основы Дискретной Математики. Информационная Математика

Подождите немного. Документ загружается.

§ 4.7. Синтез логических структур в топологических базисах 341

QB2 (рис. 4.49, б) из-за двусторонней проводимости соединитель

ных каналов и подграфы Qp\ и Qr2 (рис. 4.49, в) из-за двусторон

ней проводимости самих ключевых элементов. Для ликвидации

лишних путей, вызванных двусторонней проводимостью самих

элементов, один из элементов, находящийся на диагонали запре

щенной фигуры, ориентируется последовательным соединением с

Ним развязывающего диода.

Переход Н —ь S в базисах рассматриваемого класса осуще

ствляется, как и в первом топологическом базисе, с последующей

ориентацией диагональных ребер в запрещенных фигурах Qp.

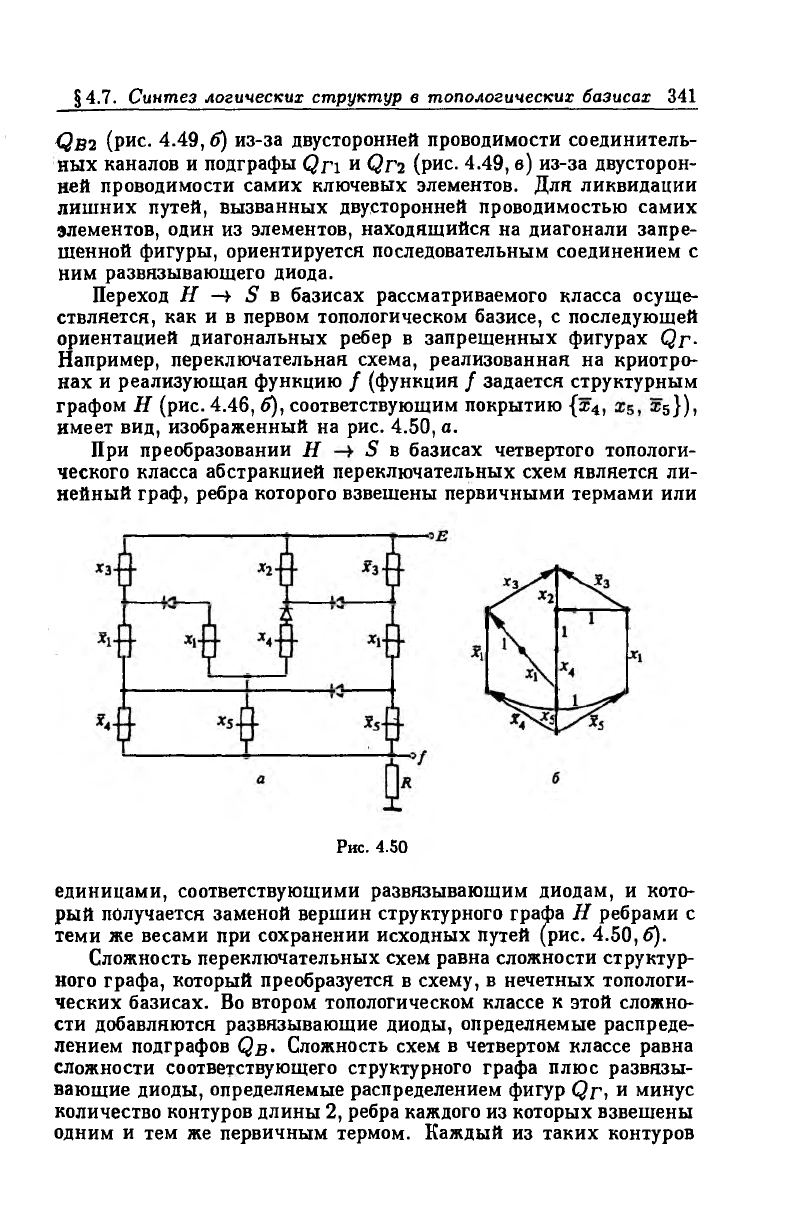
Например, переключательная схема, реализованная на криотро

нах и реализующая функцию / (функция / задается структурным

графом Н (рис. 4.46, б), соответствующим покрытию {х4, zs})i

имеет вид, изображенный на рис. 4.50, а.

При преобразовании Н S в базисах четвертого топологи

ческого класса абстракцией переключательных схем является ли

нейный граф, ребра которого взвешены первичными термами или

Рис. 4.50

единицами, соответствующими развязывающим диодам, и кото

рый получается заменой вершин структурного графа Н ребрами с

теми же весами при сохранении исходных путей (рис. 4.50,6).

Сложность переключательных схем равна сложности структур

ного графа, который преобразуется в схему, в нечетных топологи

ческих базисах. Во втором топологическом классе к этой сложно

сти добавляются развязывающие диоды, определяемые распреде

лением подграфов Qb• Сложность схем в четвертом классе равна

сложности соответствующего структурного графа плюс развязы

вающие диоды, определяемые распределением фигур Qp, и минус

количество контуров длины 2, ребра каждого из которых взвешены

одним и тем же первичным термом. Каждый из таких контуров

342

______

Гя. 4. Теория формальных грамматик и автоматов

заменяется ключевым элементом с двусторонней проводимостью

(рис. 4.51).

Таким образом, если считать только переключательные эле

менты, то сложность логических схем в топологических базисах

равна сложности соответствующего структурного графа Н и опре

деляется распределением запрещенных фигур Q a и Q e в мографе

GM, задающем реализуемую булеву функцию f(x\, х2, ..., жп)-

§4.8. Синтез логических структур в несвязных базисах

В классической теории автоматов проектирование логических

структур (схем) рассматривается в основном как тождественное

преобразование логических выражений с помощью используемой

алгебры

А = (М , fi, /2, ..., /п),

где М — носитель; /х, /2, ..., /п — операции, определяющие

сигнатуру алгебры.

Известно, что любая алгебра является аппаратом порождения

композиций по связкам, соответствующим операциям этой алгеб

ры. При этом любая операция fi определяет поведение целого

mj по поведению его частей т\, т 2, ..., rrij-i, связанных функ

цией /,:

rrij = fi (mi, т 2, ..., rrij-i). (4.20)

Но определение функционирования целого по функционирова

нию его частей является задачей анализа объекта. Таким образом,

при прямом или композиционном подходе проектирование логи

ческих схем осуществляется средствами анализа.

Наиболее эффективным аппаратом проектирования является

функциональная декомпозиция, которая, несмотря на многочис

ленные публикации по этой проблеме, оставалась открытой вплоть

до публикации работы по важному, с практической точки зре

ния, случаю минимальной повторной декомпозиции. В связи с

этим проектировщики схем довольствуются построением функци

ональных декомпозиций на основе эвристических соображений.

Об удаленности получаемых при этом решений от минимальных

говорить не приходится. Автором при декомпозиционном подходе

было предложено новое направление — направление структур

ной декомпозиции, конструктивным элементом которого является

понятие коаягебры.

§ 4.8. Синтез логических структур в несвязных базисах

343

При проектировании логических схем функционирование це

лого rrij задано, и требуется определить функционирование его

частей, связанных элементами заданного базиса и реализующих

функции /,-, т. е. найти связи между базисными элементами, об

разующими искомую схему. Другими словами, следует опреде

лить по результату m,j (j — 1)-местной операции /,■ аргументы mi,

m2, ..., mj- 1 такие, чтобы выполнялось соотношение (4.20).

Процедуру определения по rrij множества {mi, m2, ..., ^j-i}

такого, что выполняется (4.20), будем называть кооперацией

= (mi> m2) • • •,

Термин кооперация можно заменить словами обратная опе

рация.

Очевидно, что если результаты операций строго однозначны,

то результаты коопераций неоднозначны. Для уменьшения чи

сла результатов коопераций необходимо наложить ограничения на

вид искомых аргументов. Такое ограничение при синтезе логиче

ских схем вводится естественным образом; это — ограничение на

искомую схему.

Если алгебра определяет законы композиции, то коалгебра —

законы декомпозиции.

Аналогично существованию, например, алгебры Буля, алгебры

Вебба, импликативной алгебры, алгебры Жегалкина при развитии

теории коалгебр следует ожидать появления коалгебры Буля, ко-

алгебры Вебба, импликативной коалгебры, коалгебры Жегалкина.

В настоящее время разработана только коалгебра графов, яв

ляющаяся изоморфной коалгебре Буля, в которой носитель задан

диаграммами Хассе или структурными графами.

В структурном графе каждая вершина взвешена первичным

термом ' и путь взаимно однозначно соответствует максималь

ному интервалу (простой импликанте) булевой функции f(x 1,

®2) • • •) З-п)"

Коалгеброй графов называется совокупность вида

К = (М,х\х~),

где носителем М является множество всевозможных структурных

графов, а сигнатурой — кооперация дизъюнкции xv и кооперация

отрицания х~ структурных графов. В дальнейшем эти две ко

операции будем называть соответственно операцией разложения

Xv и операцией инверсии графов.

Операция разложения xv графов. При выполнении

этой операции указывают направления, по которым происходит

разложение графа Н. Направление задается вершинами, являю

щимися максимальными элементами графа Н.

Операция разложения * У(Я) графа Н по направлениям

(t = 1, ..., к) есть выделение соответственно подграфов Щ

344 Гл. 4. Теория формальных грамматик и автоматов

(г = 1, к), каждый из которых состоит из всех вершин {vj/

j = 1, ...,/} и соединяющих их дуг, для которых в графе Я най

дется путь, соединяющий va 6 {t>y/ j = 1, ..., /} и t>j 6 Vi.

Например, результат операции разложения структурного графа

Н (см. рис. 4.46,6) по направлениям {хз} и {х2, ®з} представлен

на рис. 4.52. Повторные буквы отмечаем штрихами с целью иден

тификации вершин графа.

Если вершины Vi, определяющие направления, такие, что для

всех va € {vj/ j = 1, ..., 1} выполняется va > vt, vt 6 Ц, то по

лученный подграф Щ будем называть синдромом S(VJ) вершин

Vi. Если же для всех вершин va € {«у/ j = 1, ..., f} выполняется

Va < Щ, Щ € Vi, то подграф Hi будем называть антисиндромом

S(V{) вершин Vi.

Операция инверсии х~ графов. Структурный граф,

представленный в виде суперпозиции структур типов тг и <т, назы

вается графом типа ж а (па-графом).

Операция инверсии х~(Н) структурного графа Н — это при

ведение данного графа с помощью его разложения к графу типа

жа, замена каждого подграфа типа а подграфом типа ж и каждого

подграфа типа ж подграфом типа ст; при этом каждый вес пер

воначального графа заменяется весом x(<7,+1) mod 2 на соответст

вующих вершинах полученного графа.

Утверждение. Запрещенными фигурами свойства струк

турных графов быть жа-графами являются графы, гомеоморф-

ные графам Qb « Од (рис. 4.53, о), тп. е. графы, представленные

на рис. 4.53,б.

§4.8. Синтез логических структур в несвязных базисах

345

Таблица 4.20

Следовательно, минимальное расщепление структурного графа

дри приведении его графу типа тга определяется минимальным

покрытием семантической таблицы, в которой столбцам взаимно

однозначно соответствуют запрещенные фигуры, строкам — пути

между вершинами umin и v(s+(v) = 2) и между v(s~(v) = 2) и

Umax, где v(s+(u) = 2) — вершина с положительной полустепеныо,

Т. е. с числом исходящих дуг, равным 2; v(s~(v) = 2) — вершина с

отрицательной полустепеныо,

Т. е. с числом входящих дуг,

равным 2; vmjn и vmax — ми

нимальный и максималь

ный элементы соответствую

щих путей.

При устранении запрещен

ной фигуры рассматриваемого

Свойства один из этих путей

расщепляется.

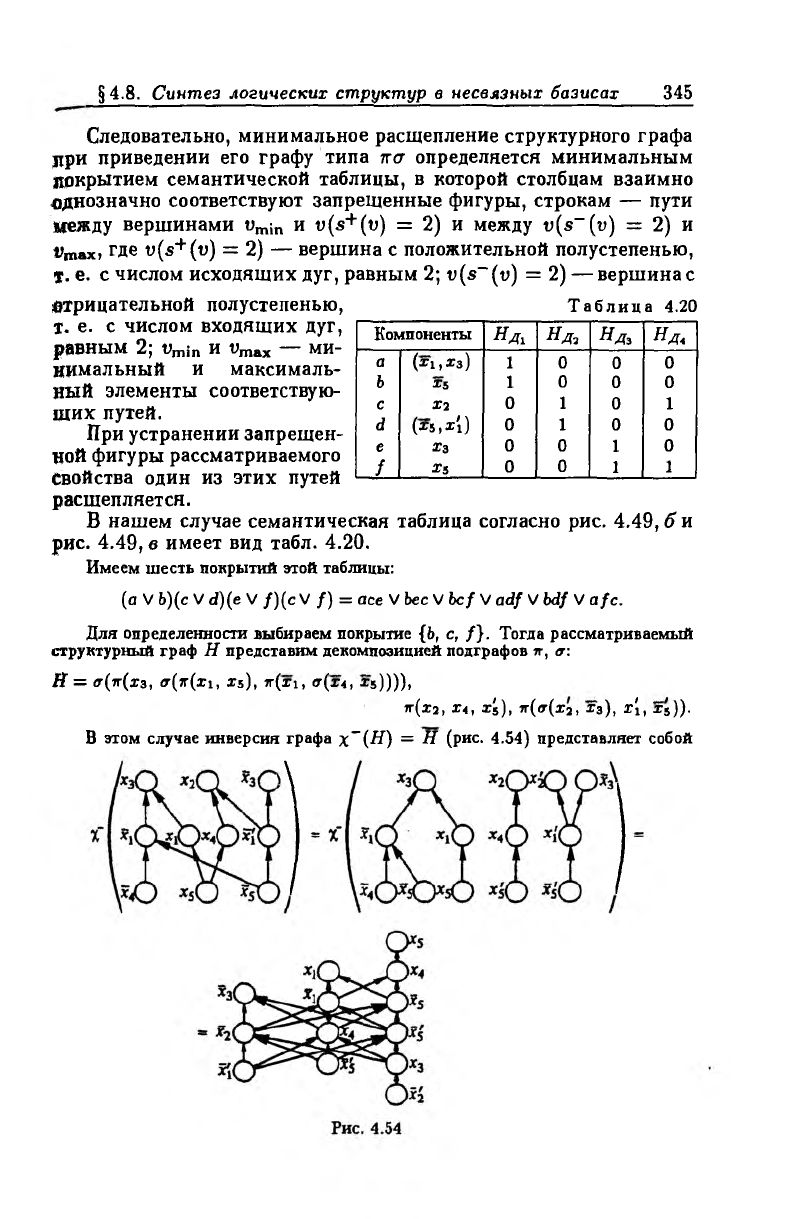
В нашем случае семантическая таблица согласно рис. 4.49, б и

рис. 4.49, в имеет вид табл. 4.20.

Имеем шесть покрытий этой таблицы:

(а V Ъ)(с V d)(e V /)(с V /) = асе V bee V Ьс/ V adf V bdf V afc.

Для определенности выбираем покрытие {Ь, с, /}. Тогда рассматриваемый

структурный граф Н представим декомпозицией подграфов тг, <г:

Я = <т(тг(хз, er(iг ( п , х 5), тг(х1, <г(х4, X s)))),

7Г(Х2, Х4, x'S), ТГ(«Т(Х2, Х з), х[, х'Ъ)).

В этом случае инверсия графа Х~(Щ = Я (рис. 4.54) представляет собой

Компоненты

На

Я д,

НДъ

Я д4

(xi,x3)

1 0

Хь

1 0 0 0

с XI 0

0 1

(xs.x'l) 0 1 0 0

Хз

0 0 1 0

Xs 0

346

Гл. 4. Теория формальных грамматик и автоматов

выражение вида

Я = 7г(<г(х3, »r(<r(xi, Х5), <г(х 1, »r(X4, Xs)))),

<г(х2, Х4, Х^). ®'(’Г(Х2, Хз), xi, Х^)).

При синтезе логических схем в функциональном базисе В не

обходимо определять результаты коопераций вида х*ь' (&«' € В),

Х/ь'(Я ) = {Яь Я2, (4.21)

где &вх — входной коэффициент элемента Ь,-.

Результат кооперации х*ь' можно получить, применяя соответ

ственно ряд коопераций вида x v и х~ в порядке, обратном порядку

следования операций V и в разложении операции /ь( на V и

Например, результаты кооперации Шеффера х'{Н) определяем с

помощью коалгебры графов следующим образом.

Пусть необходимо найти результат {Hi,H2} кооперации

Х'(Н), т. е.

*'(Я ) = {Hi, Яг}. (4.22)

Графы Hi, Яг являются результатом х!{Н), если и только если

соответствующие им функции fi(Hi) и /г(Яг) связаны (согласно

определению кооперации) соотношением

f(H) = fi(Hi)/h(H2).

Но, с другой стороны, /(Я) = fi(Hi) V f2{H2). Отсюда согласно

определению кооперации и приведенным выше уравнениям полу

чаем

XS/(H) = {Hi,H'2}, x~(H[) = Hi, х~ (н2) = н2,

т. е. в случае базиса Шеффера уравнение (4.22) можно свести к

системе тт v/rrw

Hi=X (H{exv(H)),

н2 = х~(Щ е ху(Я)).

В дальнейшем будем обозначать j-ю компоненту результата ко-

операции xfb‘(H) = {Hi, Я 2, . . Я>, . . Я*„} как хл ‘ (Я)|>, т. е.

В рассматриваемом случае уравнение (4.22) сведено к системе

ВИДЗ Я х =x~(Xv(^)|i),

Я 2 = х-(ХУ(Я) |2).

При сведении задачи определения результата {Hi, Н2, ...

..., Hktx} кооперации х*ь'{Н) к задаче определения результатов

коопераций xv и X- в сущности сводят структурное уравнение

(4.21), разрешенное относительно {Hi, Н2..., Я*,х}, к системе,

§4.8. Синтез логических структур в несвязных базисах

347

состоящей из квх структурных уравнений, причем каждое j-e

= 1, . . квх) структурное уравнение системы разрешено отно

сительно Ну.

Hi = х"и(х"12- • -(xa,ni (Я)).

Я2 = х“2,(х“г2-.-(х“2п’ (Я))

Я ;= х “>Чх“'2...(х “'п'(Я ))

(4.23)

я*„ = Ха*,х1 (х"*”2 • • .{хак'хпк (Н))...),

где xai] е {xVU, X }; * = 1, — , *вх, J = 1» — , »,■; »Ъ — целое

число, определяемое базисным элементом bj для любого j.

Система (4.23) представляет собой квх независимых друг от

друга структурных уравнений. Не для каждого базисного элемента

Ь,- 6 В можно свести решение структурного уравнения (4.21) к

решению системы уравнений вида (4.23).

Для определения вида базисного элемента, для которого реше

ние (4.21) сводится к решению (4.23), разобьем все множество

функциональных базисов на два класса: несвязных и связных ба

зисов.

Предварительно сопоставим каждому базисному элементу Ь, 6

€ В граф Ньп построенный следующим образом. Выразим буле

ву функцию реализуемую элементом Ьх, через связки V и

Полученное выражение, в котором имеются только операции дизъ

юнкции и отрицания, представим в виде графа Яь( согласно геоме

трической интерпретации /-местной операции дизъюнкции и опе

рации отрицания (рис. 4.55).

тГ(Я)={я1, нг

....

н,} Х'(Я)=я

О *

Рис. 4.55

Базис В = {Ь,/ t = l,..., п} называется несвязным, если ни

один из графов Я*,,, которые соответствуют функциям /(,■, реали

зуемым элементами базиса, не содержит цикла.

Несвязными являются, например, базисы Вебба, Шеффера,

Импликативные, коимпликативные.

Базис В = {Ь,/ i = 1,..., п} называется связным, если хотя бы

один граф (г £ {1, 2, ..., п}), который соответствует функции

348

Гл. 4. Теория формальных грамматик и автоматов

hi (* € {1, 2, . . п}), реализуемой одним из элементов базиса,

содержит цикл.

Например, решение уравнения *А(Я) = {На, Яб, Яс, Я<*}, со

ответствующего основному элементу УСЭППА (рис. 4.56), сводится

к решению системы вида

ffl = xv(x-(xv(x-(xvm |1))|3))|1,

ff« = x-<xv<x-(xv(;r(xv(tf)|!))|1))|2), (4.24)

Hj = x-(xv(x-(xv(H)|3))|2),

x-(xv(x-(xv(H)|1))|!) = x-(xv(x-(x''(ff)|J))|1).

Здесь Д — знак операции, реализуемой основным элементом

УСЭППА (универсальная система элементов промышленной

пневмо-автоматики).

Число связанных уравнений в системе вида (4.24) равно ци-

кломатическому числу графа Щг Здесь возникает задача ми

нимизации связности системы структурных уравнений, которая

сводится к эквивалентным преобразова

ниям соответствующих булевых выраже

ний. Действительно, ДНФ, соответст

вующая булевой функции УСЭППА, име

ет вид

Д(а, Ь, с, d) = аб V ас V bed,

а после применения закона де Моргана —

вид

Рис. 4.57

Д(а, Ь, с, cf) = aVbVaVcVbVcVcf.

Полученное выражение определяет граф Я*,, , представленный на

рис. 4.57. Цикломатическое число v(Hb{) этого графа равно 3:

u(Hbi) = \U\ - \V\ -I-1 = 10 - 8 + 1 = 3,

и система структурных уравнений имеет вид

tf„ = x -(x v(x -(x vm i 1))|I),

H» = x-(xv(x-(xv(H)|1))|3),

я с = х',(х~(х',(я)|2))|2,

Ht = x~(xv(x“(xv№ |3))|3),

x-(xv(x-(xv(«')|,))|I) = хЧхЧхЧхЧяЦХ).

x-(xv0r(xv(H)|1'))|1) = х*(х~(х'/(Я)|3))|1,

xv(x-(xv(H)|!))|2 = x-(xv(x-(xv(«)|3))l2)-

(4.25)

§ 4.8. Синтез логических структур в несвязных базисах

349

Используя законы булева анализа, систему (4.25) упрощаем до

системы (4.24). Минимизация цикломатического числа графа Нь{

осуществляется с помощью функциональной декомпозиции путем

роиска эквивалентных булевых выражений.

В общем случае определение результатов кооперации в связ

ных базисах сводится к решению системы связных структурных

уравнений вида

*0» (х&2... (х*"*(Я))...) = х»» (х722... (х”»*а (Я))...),

(хД* ... (х&""р(Я))...) = х ^ (*•>’ ...(x>fc*(Я)) ...),

ляются элементом 6, соответственно для любого ja, jp, j\; ip, t7 =

= 1, ..., p (p — число линейно независимых циклов в графе Я(Ь,),

При синтезе логических схем в функциональных базисах стро

им по реализуемой функции / структурный граф, который за

тем с помощью коалгебры графов преобразуем в функциональный.

Полученный функциональный граф и является искомой логиче

ской схемой. Предположим следующую процедуру преобразования

структурного графа в функциональный. Предлагаемый ниже ал

горитм рассмотрим на примере синтеза функционального графа,

реализующего булеву функцию от трех переменных счетчика чет

ности в базисе В = {-+, 0}.

Алгоритм состоит из следующих шагов.

1. Структурный граф Ь € В, реализующий булеву функцию /,

сопоставляется максимальному элементу графа Нь, соответствую

щего базисному элементу Ъ € В.

2. Согласно графу Щ, определяющему функционально-струк

турные свойства элемента b 6 В, выполняются соответствующие

операции разложения и инверсии над графом Я/.

3. В результате выполнения операций п. 2 определяются струк

турные графы Я/,, соответствующие минимальным элементам

графа Нь-

Заметим, что максимальный элемент графа Нь соответствует

выходу базисного элемента Ь, минимальные — входам этого эле

мента.

Нх = х"» (х“12... (x“‘"i (Я))...),

Я2 = х“« (Xе" ... (xa s "2 (Я))...),

Hj = Xе* (х“^ ... (хау"У (Я))...),

Я*,х = х а*«1(х а,'« 2. . . (х"*,хП*« (Я))...), (4.26)

х*“ (х*» ...(х^-ч (Я))...) = х™ (х™ ... (х™ ! (Я))...),

ГДе x"*aJa , X*V/> , x'Y‘l,J'T 6 {xV

• • v nai jfi — 1) • • •) jy “ 1)

равное его цикломатическому числу 1/(Я(6,)).

350

Гл. 4. Теория формальных грамматик и автоматов

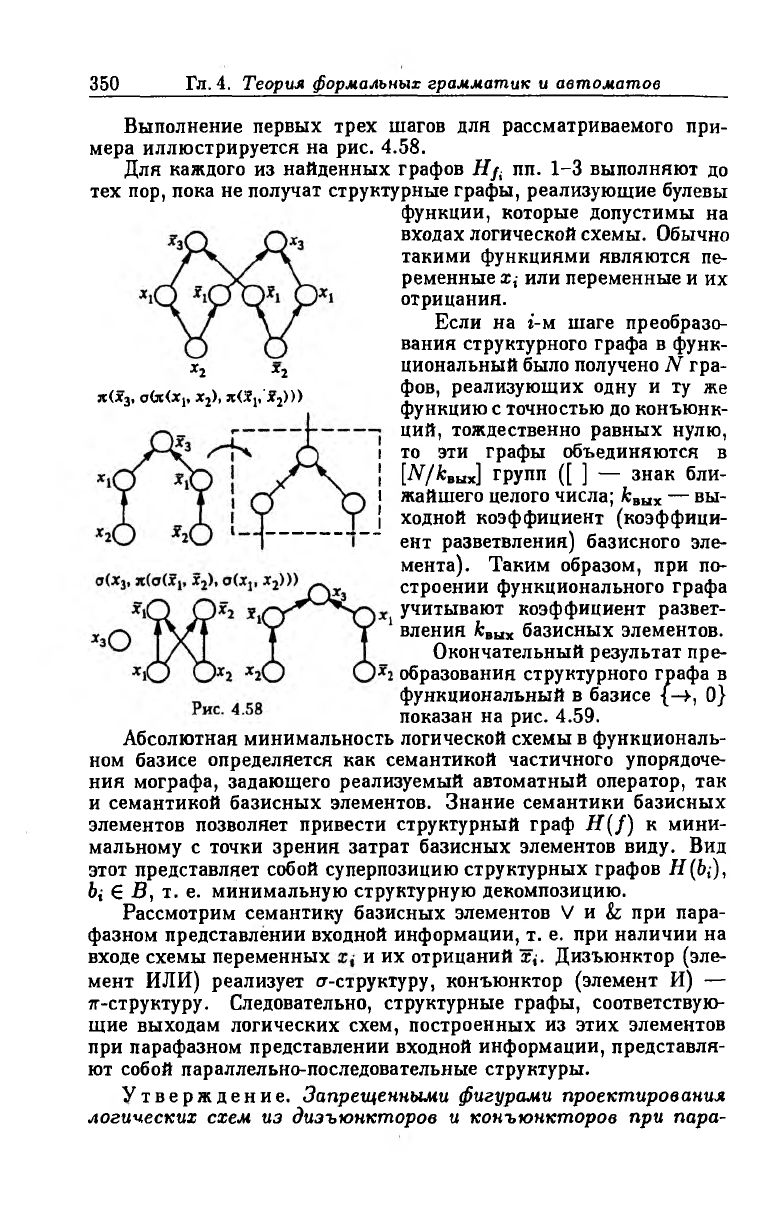
Выполнение первых трех шагов для рассматриваемого при

мера иллюстрируется на рис. 4.58.

Для каждого из найденных графов Hj{ пп. 1-3 выполняют до

тех пор, пока не получат структурные графы, реализующие булевы

функции, которые допустимы на

входах логической схемы. Обычно

такими функциями являются пе

ременные Х{ или переменные и их

отрицания.

Если на i-м шаге преобразо

вания структурного графа в функ

циональный было получено N гра

фов, реализующих одну и ту же

функцию с точностью до конъюнк

ций, тождественно равных нулю,

то эти графы объединяются в

[Л7А;ВЫХ] групп ([ ] — знак бли

жайшего целого числа; квь1х — вы

ходной коэффициент (коэффици

ент разветвления) базисного эле

мента). Таким образом, при по

строении функционального графа

учитывают коэффициент развет

вления квах базисных элементов.

Окончательный результат пре

образования структурного графа в

функциональный в базисе {—», 0}

показан на рис. 4.59.

Абсолютная минимальность логической схемы в функциональ

ном базисе определяется как семантикой частичного упорядоче

ния мографа, задающего реализуемый автоматный оператор, так

и семантикой базисных элементов. Знание семантики базисных

элементов позволяет привести структурный граф H(f) к мини

мальному с точки зрения затрат базисных элементов виду. Вид

этот представляет собой суперпозицию структурных графов Я(Ь,),

bi € В, т. е. минимальную структурную декомпозицию.

Рассмотрим семантику базисных элементов V и & при пара-

фазном представлении входной информации, т. е. при наличии на

входе схемы переменных и их отрицаний х,-. Дизъюнктор (эле

мент ИЛИ) реализует ст-структуру, конъюнктор (элемент И) —

тг-структуру. Следовательно, структурные графы, соответствую

щие выходам логических схем, построенных из этих элементов

при парафазном представлении входной информации, представля

ют собой параллельно-последовательные структуры.

Утверждение. Запрещенными фигурами проектирования

логических схем из дизъюнкторов и конъюнкторов при пара-

х2 х2

я<г3, ote<Xi, х2), хО^,’^)))