Горбатов В.А. Фундаментальные Основы Дискретной Математики. Информационная Математика

Подождите немного. Документ загружается.

§ 4.7. Синтез логических структур в топологических базисах 311

Множество топологических базисов в свою очередь разобьем

на четыре класса. Первый и второй классы образуют элементы,

пропускающие информационный сигнал в одном направлении при

совпадении значения управляющего сигнала с буквой, взвешиваю

щей этот элемент. Но в элементах первого класса прошедший

сигнал распространяется по каналам с односторонней проводи

мостью, а в элементах второго класса — по каналам с двусторон

ней проводимостью.

К первому классу относятся диодно-вентильные элементы, в

случае оптической обработки информации с использованием воло

конной техники — переключатели света, ко второму — вентиль

ные элементы (например, спейсистор-триод).

На входах схемы, составленной из рассматриваемых элемен

тов, как и на входах системы, построенной из элементов любого

топологического базиса, используется парафазное представление

двоичной информации.

Третий и четвертый классы образуют элементы, пропускаю

щие информационный сигнал в обоих направлениях при совпа

дении значения управляющего сигнала с буквой, взвешивающей

Этот элемент.

В элементах третьего класса прошедший сигнал распростра

няется по каналам с односторонней проводимостью, а в элементах

четвёртого класса — по каналам с двусторонней проводимостью.

К элементам третьего класса относятся, например, туннель-

троны и диодно-контактные элементы; к элементам четвертого —

ключевые элементы с двусторон

ней проводимостью (криотроны,

контакты).

Таким образом, все множество

топологических базисов разбито

на четыре класса по двум призна

кам: по проводимости элемента и

по проводимости соединительного

канала.

Основой элементов третьего

класса является нейрон, формальная модель которого предложена

американскими учеными У. Мак-Каллоком и У. Питсом и развита

С. Клини, Д. Калбертсоном, Дж. фон Нейманом и другими. Усло

вия возбуждения нейрона описываются функцией вида

^0 в противном случае,

где х,- = 0, 1; и>,- — вес t-ro синапса (места контакта аксона и тела

нейрона (рис. 4.33)); Р — порог возбуждения нейрона.

312

Гл. 4. Теория формальных грамматик и автоматов

Фиксацией весов синапсов и порога нейрон настраивается на

реализацию любой булевой функции от к переменных.

В качестве функционала качества проектируемой схемы возь

мем количество переключательных элементов, содержащихся в

ней. Этот функционал в дальнейшем будем называть слож

ностью L(S) схемы S.

Рассмотрим проектирование логических схем в топологиче

ских базисах первого класса на примере булевой функции /(х^,

Х2,. . хп), заданной своей дизъюнктивной нормальной формой

(ДНФ):

f(xi, Х2, . . ., Хп) = Х4Х5Х9 V X1X5Z10 V XiX2X3X4X5 V

V X5X9X11 V X1X2Z6 V XgXgXn V Х7Х9ХЦ V Х2Х3Х7 V

V Х1 Х5ХЦ V Х3Х4Х8 V Х1 Х8ХЦ V Х1 Х7 ХЦ.

Каждая простая импликанта реализуемой булевой функции

взаимно однозначно соответствует пути в структурном графе. При

этом первичные термы х*‘, входящие в простую импликанту, взве

шивают вершины соответствующего пути.

Реализуемая булева функция / определяется моделью Фа(/):

*.(/) = S3> S5>, S3CV3, SSCV5,

V = {xi,. X2, X3, X4, X5, Xg, X7, X8, X9, X10, xu },

S3 = {{x4, x5, x9}, {xi, x5, Xio}, {x5, X9, xu) , {xx, x2, x6) ,

12 4 5

{x8, x9, Xu}, {x7, x9, xn }, {x2, X3, X7}, {xi, X5, XU},

6 7 8 9

{I3, X4, Xe}, {®1, *8) г и }) 1) X7) Xll}})

.....

...

......

s V /

....

...

10 11 12

■$>= { { *1 , *3, X3, x 4, x 5}}.

Зададим модель Фa(f) в виде мографа, при этом роль букв

играют первичные термы, слов — простые импликанты.

Задание булевой функции в виде мографа позволяет наряду с

чисто логическими свойствами функции исследовать ее частотные

и топологические свойства, что позволяет естественным образом

рассматривать проектирование булева графа как преобразование

мографа в диаграмму Хассе, задающую частично упорядоченное

множество.

Вершина v называется разделяющей в структурном графе, ес

ли любой путь графа содержит ее.

Подграф Г структурного графа называется гамаком, если лю

бой его (подграфа) путь содержит две разделяющиеся вершины,

являющиеся соответственно минимальным и максимальным эле

ментами этого подграфа.

§ 4.7, Синтез логических структур в топологических базисах 313

Замена минимального элемента гамака Г на максимальный

И наоборот с одновременным изменением ориентации всех дуг

«На противоположное называется операцией взятия двойственной

Структуры от гамака Г.

Синтезируем структурный граф последовательным построени

ем путей, соответствующих рассматриваемым простым импликан-

там. При эхом построении выполнением операции взятия двой

ственной схрукхуры будем сопосхавляхь общим частям в просхых

импликантах общие части в схрукхурном графе. Если такое сопо

ставление выполнить нельзя, так как в графе возникают лишние

пути (т. е. пути, взвешенные конъюнкциями, не содержащимися

;в заданной ДНФ булевой функции), то производим расщепление

.первичного терма, т. е. сопоставление первичному терму более

!рдной вершины в структурном графе. Естественно, что при од

ном расщеплении сложность схемы возрастает на единицу. Далее,

Очевидно, что сложносхь схемы не можех быхь меньше мощносхи

носителя мографа, определяющего реализуемую булеву функцию,

так как носихель сосхоих из сушесхвенных переменных.

Будем рассмахривахь просхые импликанхы в порядке их напи

сания в ДНФ. В мографе они помечены соохвехсхвующими иден

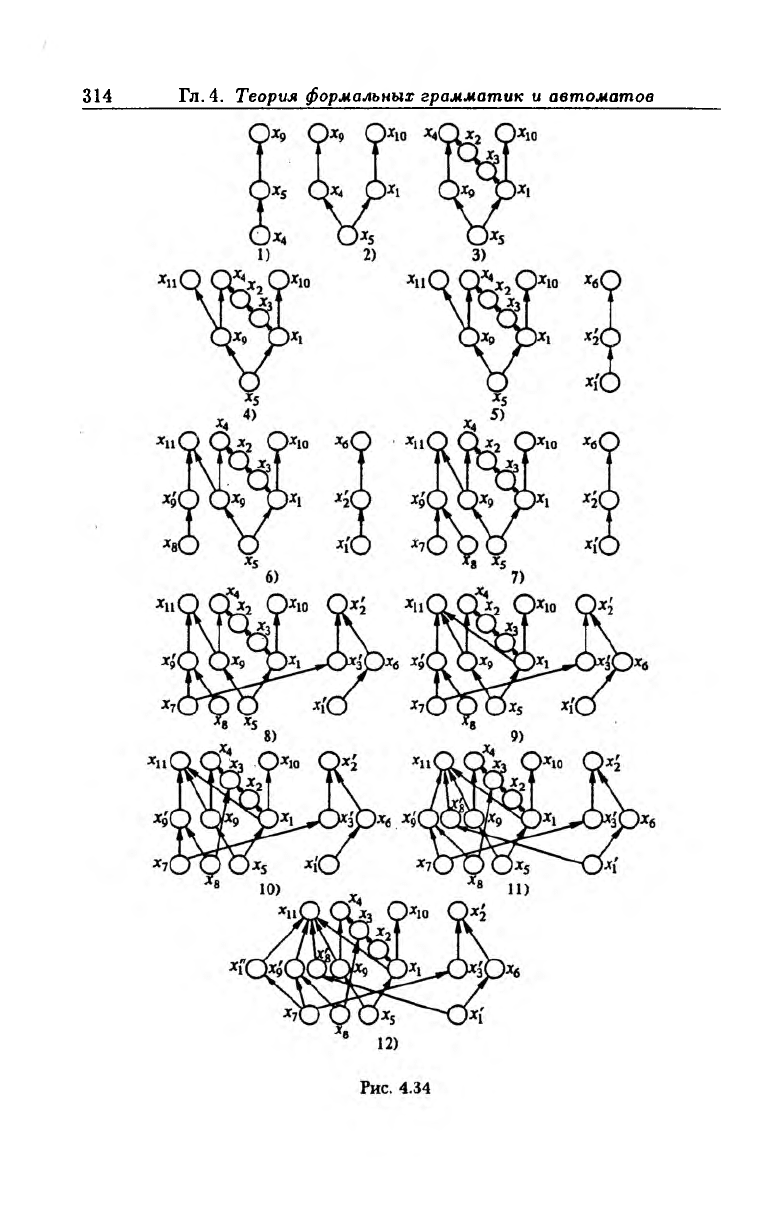
тификаторами. Последовательное построение структурного графа

^изобразим на рис. 4.34 на котором числа 1-12 обозначают присое

динение очередного пути, соответствующего следующей простой

Импликанте, идентификатор которой совпадает с номером, указан

ным под графом.

1) Задаем отношение упорядоченности в первой простой им-

'■Пликанте Х4Х5Х9: «(*4) < u(xs) < vXg. Здесь и ниже запись v(xj')

^означает вершину диаграммы, взвешенную термом х .

2) Присоединяем вторую простую импликанту. Чтобы не рас

цеплять первичный терм х5 в построенной на первом шаге диа

грамме, выполняем операцию взятия двойственной структуры от

Гамака Гг = (V^, Uri), Vr, = {z4, *5}, Ur, = {(x4, x5)}- В ре

зультате получаем диаграмму

Н2 = (V2, U2), V2 = {xi, x4, x5, X9, xio},

U2 - {(*5, *4), (X4, X9), (*5, Xi), (*1 , Х10)},

соответствующую первым двум простым импликантам.

3) Аналогично при построении третьего пути, соответствую

щего простой импликанте XiX2X3X4X5, выполняем операцию взя

тия двойственной структуры от гамака Г2 = (Vr2, СТг2) > Vr2 =

'# {*4, *9}, Ur2 = {(х4, Х9)}.

Окончательно получаем диаграмму

Я 3 = (V3, U3), Уз = {*1, Z2,Z3,*4,X5,X9,X10},

Vz — 2-9)) (x5f Xi), (xq, x4), (xi, x10),

(xi, 13), (x3, X2), (x2, x4)}.

314

______

Гл. 4. Теория формальных грамматик и автоматов

§4.7. Синтез логических структур в топологических базисах 315

4) Присоединяем путь v(xs) < и(х9) < и(хц), соответствую

щий четвертой простой импликанте. Имеем диаграмму

На = (VA, UA), V4 = {*1, Х2, *3, *4i ®5i *9, *10i *ll},

t/4 = {(z5,X9), (*5.*l). (*9 ,*и), (x9,X4),

(Xi,Xio), (x i,i3), (хз,х2), (x2, X4)}.

5) Построение следующего пути, реализующего простую им-

пликанту х\х2х&, приводит к противоречию в диаграмме, если не

производить расщепление первичных термов i j и i 2, так как по

строение этого пути с включением в него вершин диаграммы Я 4,

взвешенных х\ или х2, приводит к возникновению лишних путей.

Расщепление отмечаем штриховкой первичного терма.

Аналогично строим всю диаграмму, реализующую заданную

булеву функцию:

# 12 = <Vl2, U12), Vi2 = {Xi, Х^ x", X2, X2, X3, X3, x4, x5, x6,

XT, x8, Xg, x9, x'9, x10, xn },

Ul2 = {(x7, Xg), (x7, X?), (*7, X3), (x8, Xg), (x8, *3),

(15, X9), (xs, Xl), (®i, Xg), (xi, Xg), (x9, 111), (Xg, Ill)|

(xj, Хц), (xg, Хц), (xg, X4), (Xi, Хц), (X\, X2), (X2, X3),

(x3, X4), (Xl, X10), (хз, x'2), (x6, x2)j,

Ее сложность L(H) равна 17 (было произведено шесть расщепле

ний).

Какова близость полученной сложности к абсолютно мини

мальной? Чтобы ответить на этот вопрос, необходимо породить

все эквивалентные решения и сравнить их по сложности получен

ных структурных графов, что равно всевозможным способам упо

рядочения первичных термов в простых импликантах. В данном

случае это число равно 43 535 646 720, так как количество различ

ных упорядочений слов мографа равно П 1в»1-> где ls«l — число

букв в t-м слове. ‘

Тем не менее можно ответить на поставленный вопрос без пе

ребора всех эквивалентных диаграмм Хассе, зная при этом се

мантику (смысл) проводимого преобразования мографа GM(f) в

структурный граф # (/), GM(f) #(/) (см. теорему 3.47).

Рассмотрим, например, синтез структурного графа H(f), определяемого

счетчиком четности: выходной канал принимает значение 1, когда возбуждено

четное количество входных каналов. Рассматриваемую булеву функцию от трех

переменных, задающую работу счетчика четности, можно рассматривать как мо

дель

Ф = (М , S3), М = {xit Xi! i = 1, 2, 3},

{ti, хг, д3), {дь х2, хз), {гь х2, гз), {л, х2, г3} € 5з

12 3 4

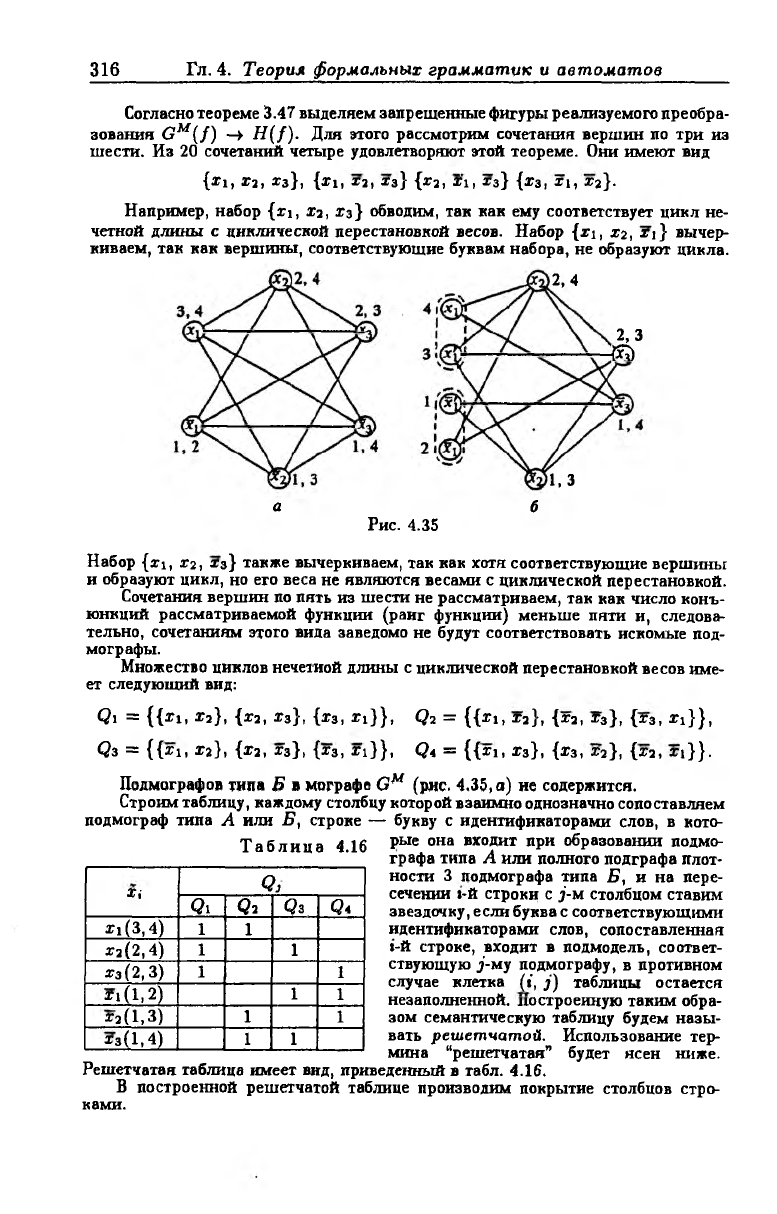
и задавать ее в виде (рис. 4.35, а).

316

Гл. 4. Теория формальных грамматик и автоматов

Согласно теореме 3.47 выделяем запрещенные фигуры реализуемого преобра

зования GM{f) —► H(f). Для этого рассмотрим сочетания вершин по три из

шести. Из 20 сочетаний четыре удовлетворяют этой теореме. Они имеют вид

{xi, хз, агз}, {*1, хз, х3} {х2, Xi, х3} {х3, х\, х2}.

Например, набор {xi, х2, хз} обводим, так как ему соответствует цикл не

четной длины с циклической перестановкой весов. Набор {xi, хг, xi} вычер

киваем, так как вершины, соответствующие буквам набора, не образуют цикла.

2,4

2,3

К)

1,3

а б

Рис. 4.35

Набор {xi, Х2, хз} также вычеркиваем, так как хотя соответствующие вершины

и образуют цикл, но его веса не являются весами с циклической перестановкой.

Сочетания вершин по пять из шести не рассматриваем, так как число конъ

юнкций рассматриваемой функции (ранг функции) меньше пяти и, следова

тельно, сочетаниям этого вида заведомо не будут соответствовать искомые под-

мографы.

Множество циклов нечетной длины с циклической перестановкой весов име

ет следующий вид:

Qi = {{ x i, х 2}, {х2, Хз}, {хз, X i}}, Q 2 = { {x i, х 2}, {х2, х3}, {хз, Xi}},

Яз = {{xi, х2}, {х2, хз}, {хз, Xl}}, Qi = {{xi, хз}, {х3, х2}, (х2, xi}}.

Подмографов типа Б в мографе GM (рис. 4.35, а) ие содержится.

Строим таблицу, каждому столбцу которой взаимно однозначно сопоставляем

подмограф типа А или Б, строке — букву с идентификаторами слов, в кото-

Таблица 4.16 РЬ1е она входит при образовании подмо-

графа типа А или полного подграфа плот

ности 3 подмографа типа Б, и на пере

сечении »-й строки с j-м столбцом ставим

звездочку, если буква с соответствующими

идентификаторами слов, сопоставленная

»-й строке, входит в подмодель, соответ

ствующую j-му подмографу, в противном

случае клетка (i, j) таблицы остается

незаполненной, построенную таким обра

зом семантическую таблицу будем назы

вать решетчатой. Использование тер

мина “решетчатая” будет ясен ниже.

Решетчатая таблица имеет вид, приведенный в табл. 4.16.

В построенной решетчатой таблице производим покрытие столбцов стро

ками.

Q i

<?2

Xi (3,4)

х 2 ( 2 , 4)

х3(2,3)

x i(1,2)

х2(1,3)

1 1

хз(1,4)

1 1

§ 4.7. Синтез логических структур в топологических базисах 317

Для рассматриваемого примера имеем покрытия: первая, четвертая строки;

вторая, пятая строки; наконец, третья, шестая строки.

Буквы, соответствующие строкам найденного покрытия решетчатой табли

цы расщепляются, т. е. в одном из слов эта буква переименовывается. При

расщеплении буквы, соответствующей »-й строке, все подмодели вида Фр (2, 1),

Которые соответствуют столбцам, на пересечении которых с i-й строкой нахо

дится 1 в решетчатой таблице, понижают свой порядок иа единицу, т. е. преобра

зуются в подмодели нулевого порядка. Данное утверждение справедливо согласно

Основному свойству квазиполных моделей.

В результате расщепления всех букв, соответствующих строкам найденного

Покрытия решетчатой таблицы ТДНФ функции / преобразуется в решетчатую

дизъюнктивную нормальную форму (РНДФ) функции /.

г Дизъюнктивная нормальная форма (ДНФ) функции /, для ко

торой существует такое взаимно однозначное соответствие между

Первичными термами и вершинами структурного графа, что вы

полняется взаимно однозначное соответствие между конъюнкция

ми и путями графа, причем вершинам каждого пути сопоставлены

первичные термы, образующие соответствующую конъюнкцию, и

дизъюнкция конъюнкций соответствует объединению соответству

ющих путей, называется решетчатой ДНФ (РДНФ) функции /.

Сложностью РДНФ функции f называется число вершин со

ответствующего структурного графа. Как будет видно, сложность

РДНФ в основном определяет сложность искомого функциональ

ного графа при структурном синтезе автомата.

Минимальной РДНФ (МРДНФ) функции f называется РДНФ

функции /, имеющая минимальную сложность из всех РДНФ, со-

|(цветствующих функции /.

Для поиска МРДНФ функции / необходимо произвести пере

бор всех РДНФ для всех ТДНФ функции / и выбрать РДНФ с

минимальной сложностью.

Каждое покрытие решетчатой таблицы соответствует РДНФ ту

пиковой ДНФ функции /.

В рассматриваемом примере все три покрытия равносильны.

Каждому из них соответствует РДНФ сложности 8. Для определен

ности выберем первое покрытие. После расщепления первичных

Термов х\ и xi получаем РДНФ функции / вида

f(xi, х[, х2, Хз) = х^хгХз V xix2x3V а^х2х3 У xix2x3.

Эта РДНФ является минимальной, так как функция / име

ет одну ТДНФ, для которой полученная РДНФ является ми

нимальной. Полученному решению соответствует мограф GM

||>ис.4.35,б)

Не строя структурного графа, можно говорить о его сложно

сти в силу взаимно однозначного соответствия между первичными

Термами реализуемой РДНФ и вершинами синтезируемого графа.

Сложность синтезируемого графа равна сложности реализуемой

РДНФ. Это свойство предлагаемого метода решетчатых таблиц поз

318 Гл. 4. Теория формальных грамматик и автоматов

воляет существенно снижать трудоемкость при синтезе минималь

ных булевых графов.

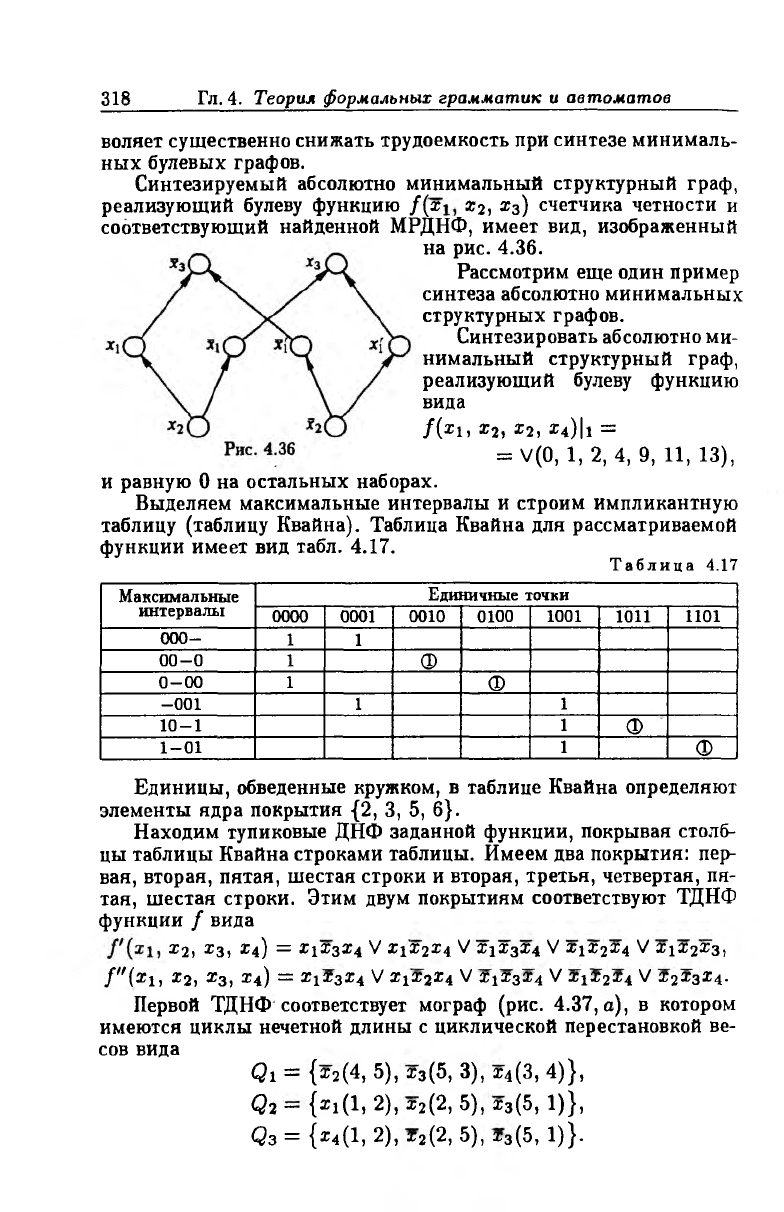
Синтезируемый абсолютно минимальный структурный граф,

реализующий булеву функцию f(x х2, х3) счетчика четности и

соответствующий найденной МРДНФ, имеет вид, изображенный

на рис. 4.36.

Рассмотрим еще один пример

синтеза абсолютно минимальных

структурных графов.

Синтезировать абсолютно ми

нимальный структурный граф,

реализующий булеву функцию

вида

/(*1, х2, *2, x4)|i =

= V(0, 1,2, 4, 9, 11,13),

и равную 0 на остальных наборах.

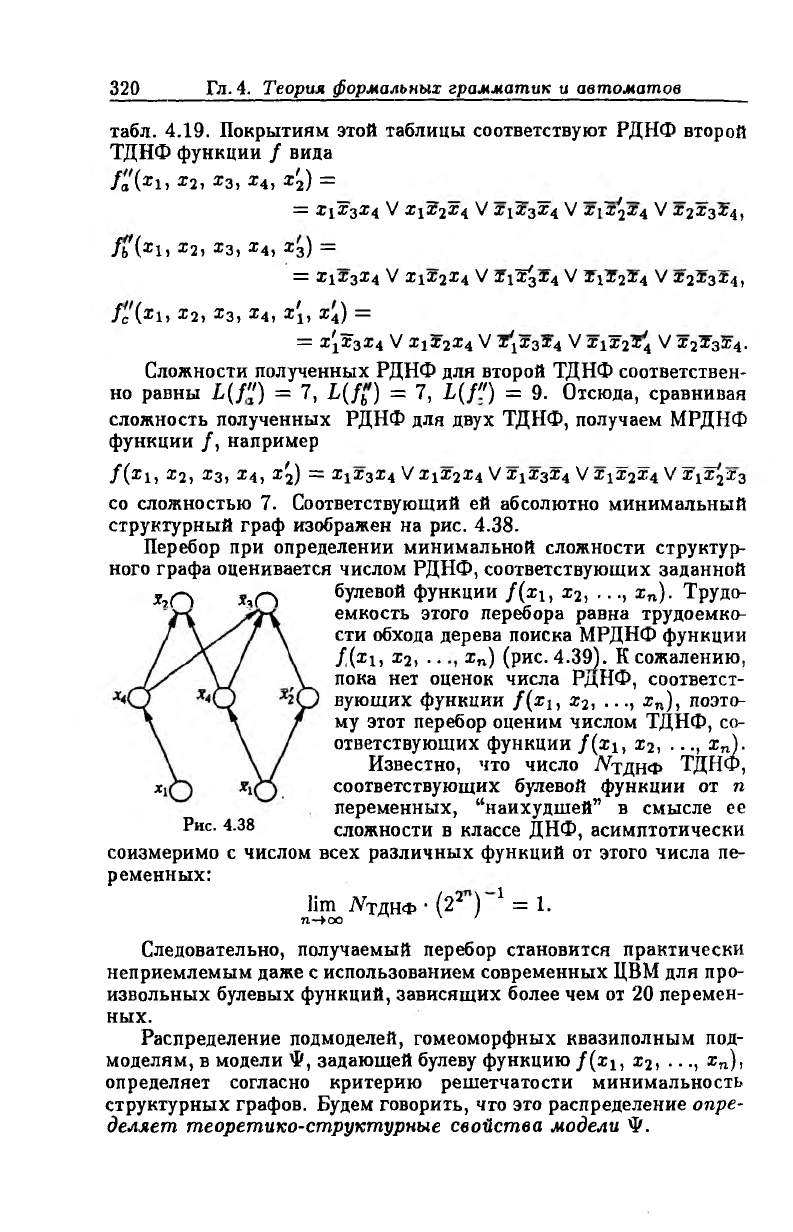
Выделяем максимальные интервалы и строим импликантную

таблицу (таблицу Квайна). Таблица Квайна для рассматриваемой

функции имеет вид табл. 4.17.

Таблица 4.17

Максимальные

интервалы

Единичные точки

0000 0001 0010

0100 1001

1011 1101

000-

00-0 1

0-00 1

-001 1

10 - 1

1-0 1

Единицы, обведенные кружком, в таблице Квайна определяют

элементы ядра покрытия {2, 3, 5, 6}.

Находим тупиковые ДНФ заданной функции, покрывая столб

цы таблицы Квайна строками таблицы. Имеем два покрытия: пер

вая, вторая, пятая, шестая строки и вторая, третья, четвертая, пя

тая, шестая строки. Этим двум покрытиям соответствуют ТДНФ

функции / вида

Х2, Хз, Х4) = ХгХ3Х4 V х{х2х4 V Х1Х3Х4 V Х1Х2Х4 V XiX2X3,

f"{x 1, х2, х3, х4) = xix3x4 V х{х2х4 V xix3x4 V xi*2x4 V 12X3X4.

Первой ТДНФ соответствует мограф (рис. 4.37, а), в котором

имеются циклы нечетной длины с циклической перестановкой ве

сов вида

Q1 = {х2(4, 5), х3(5, 3), х4(3, 4)},

Qi - { *i(l, 2), х2(2, 5), х3(5, 1)},

<Эз = {х4(1, 2), х2(2, 5), 13(5, 1)}.

§4.7. Синтез логических структур в топологических базисах 319

Решетчатая таблица, соответствующая первой ТДНФ, имеет

вид, приведенный в табл. 4.18. Решетчатая таблица имеет покры

тия: вторая и третья строки (первое покрытие); третья и четвер

тая строки (второе покрытие); первая, шестая и седьмая строки

(третье покрытие). Этим покрытиям соответствуют РДНФ первой

ТДНФ функции / вида

f'a(Xь *2) *3, *4. *г) =

= Х1Х3Х4V Х{Х2Х4V Z1Z3Z4V V Х1Х2Х3,

/j(x 1, Х2, Хз, х4, х'з) =

= X1X3X4V X1X2X4V X1X^X4V *1*2*4 V X1X2X3,

f'(xi, Х2, Хз, * 4 , xi, х'4) =

= Х^ХзХ4 V Х1 Х2Х4 V Х{ХЗХ'А V Х1Х2Х4 V * 1 X2X3 .

Таблица 4.18 Таблица 4.19

Q j

Яг

Яз

* 1( 1 ,2 )

*а (4 , 5)

*а (2, 5)

гз(5, 3) 1

*з (5, 1)

* 4(3, 4)

* 4(1, 2)

Q2 <?з

* i( l,2 )

*г (2, 5)

* i ( 3, 4) 1

*з (5, 1)

* 2(4 , 5) 1 1

*з (5, 3) 1 1

* 4(3, 4) 1

Сложности решетчатых ДНФ соответственно равны L(f^) = 7,

L{fb) — 7, L(f'c) = 9.

Второй ТДНФ функции / соответствует мограф (см. рис. 4.37),

в котором имеются циклы нечетной длины с циклической пере

становкой весов вида

Qi = /xi(l, 2), х2(2, 5), х3(5, 1)),

Q2 = |xi(3, 4), х2(4, 5), *3(5, 3)},

Q3 = {х4(3, 4), х2(4, 5), ®3(5, 3)}.

Решетчатая таблица, соответствующая второй ТДНФ, имеет вид

320

Гл. 4. Теория формальных грамматик и автоматов

табл. 4.19. Покрытиям этой таблицы соответствуют РДНФ второй

ТДНФ функции / вида

/«(*ь х2, *з, х4, х'2) =

= х\хзх4 V £1X2X4 V Х1Х3Х4 V xix^x4 V х2X3X4,

/ь'(г 1. *3, ХЗ, *4, *з) =

= Х1Х3Х4 V Х1Х2Х4 V x i4 x 4 V Х1Х2Х4 V х2X3X4,

/с (*ь *а. х3, *4. xi, Х4 ) =

= 1^ 3X4 V Х1Х2Х4 V xix3x4 V XiX2X^ V X2X3X4.

Сложности полученных РДНФ для второй ТДНФ соответствен

но равны L(f") = 7, Х(/ь') = 7, .£(/") = 9. Отсюда, сравнивая

сложность полученных РДНФ для двух ТДНФ, получаем МРДНФ

функции /, например

/(Xl, х2, Х3, х4, х'2) = Х1Х3Х4 V xix2x4 V Х1Х3Х4 V xix2x4 V Х1Х2Х3

со сложностью 7. Соответствующий ей абсолютно минимальный

структурный граф изображен на рис. 4.38.

Перебор при определении минимальной сложности структур

ного графа оценивается числом РДНФ, соответствующих заданной

ЪГ) ЪО булевой функции /(хь х2, ..., хп). Трудо

емкость этого перебора равна трудоемко

сти обхода дерева поиска МРДНФ функции

f(x\, х2, . . хп) (рис. 4.39). К сожалению,

пока нет оценок числа РдНФ, соответст

вующих функции /(хj, х2, ..., хп), поэто

му этот перебор оценим числом ТДНФ, со

ответствующих функции /(х 1, Х2, ..., хп).

Известно, что число тУтднф ТДНФ,

xj соответствующих булевой функции от п

переменных, “наихудшей” в смысле ее

Рис. 4.38 сложности в классе ДНФ, асимптотически

соизмеримо с числом всех различных функций от этого числа пе

ременных:

lim Л^тднф • (22 ) 1 = 1.

п-юо ' '

Следовательно, получаемый перебор становится практически

неприемлемым даже с использованием современных ЦВМ для про

извольных булевых функций, зависящих более чем от 20 перемен

ных.

Распределение подмоделей, гомеоморфных квазиполным под

моделям, в модели Ф, задающей булеву функцию /(хь х2, ..., хп),

определяет согласно критерию решетчатости минимальность

структурных графов. Будем говорить, что это распределение опре

деляет теоретико-структурные свойства модели Ф.