Горбатов В.А. Фундаментальные Основы Дискретной Математики. Информационная Математика

Подождите немного. Документ загружается.

§5.1. Принципы характеризационного анализа

391

Если мощность портфеля 2 < \к\ < £o(<2cb)i где £о(<2св) —

число внутренней устойчивости или вершинное число независи-

и 6

а б

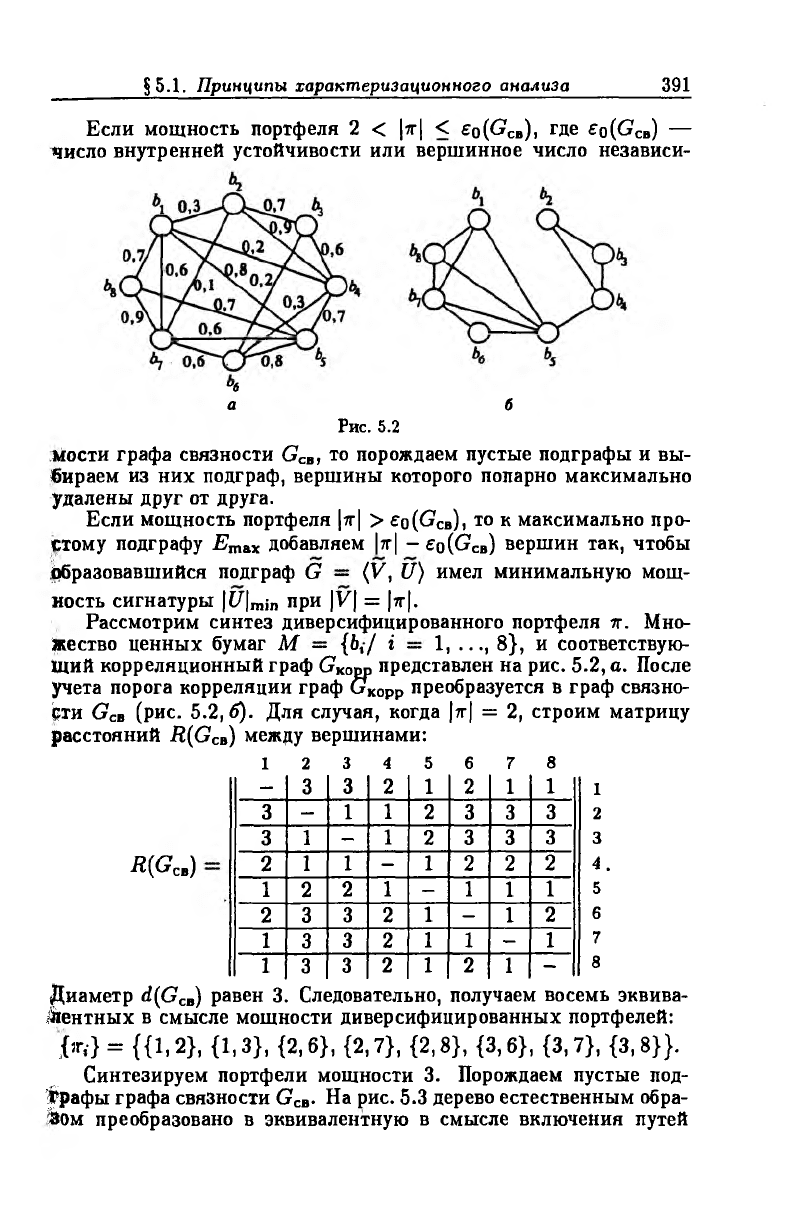
Рис. 5.2

мости графа связности GCB, то порождаем пустые подграфы и вы

бираем из них подграф, вершины которого попарно максимально

удалены друг от друга.

Если мощность портфеля \к\ > eo^aOi то к максимально про

стому подграфу Еща.х добавляем |7r| — £q{Gcb) вершин так, чтобы

Образовавшийся подграф G — {V, U) имел минимальную мощ

ность сигнатуры |J7|mj„ при |У| = |7г|.

Рассмотрим синтез диверсифицированного портфеля ж. Мно

жество ценных бумаг М — {Ь,/ i — 1, ..., 8}, и соответствую

щий корреляционный граф GKOpp представлен на рис. 5.2, а. После

учета порога корреляции граф GKOpp преобразуется в граф связно

сти GCB (рис. 5.2,6). Для случая, когда |тг| = 2, строим матрицу

расстояний R(GCb) между вершинами:

1 2 3 4 5 6 7 8

R(GCB)

—

3 2 1 2 1

3 3

- 1

2 3 3

2 2

1 - 1

2 3

3 2

1 1

2 1 2

4 .

Диаметр d(GCB) равен 3. Следовательно, получаем восемь эквива

лентных в смысле мощности диверсифицированных портфелей:

£г,-}= {{1,2}, {1,3}, {2,6}, {2,7}, {2,8}, {3,6}, {3,7}, {3,8}}.

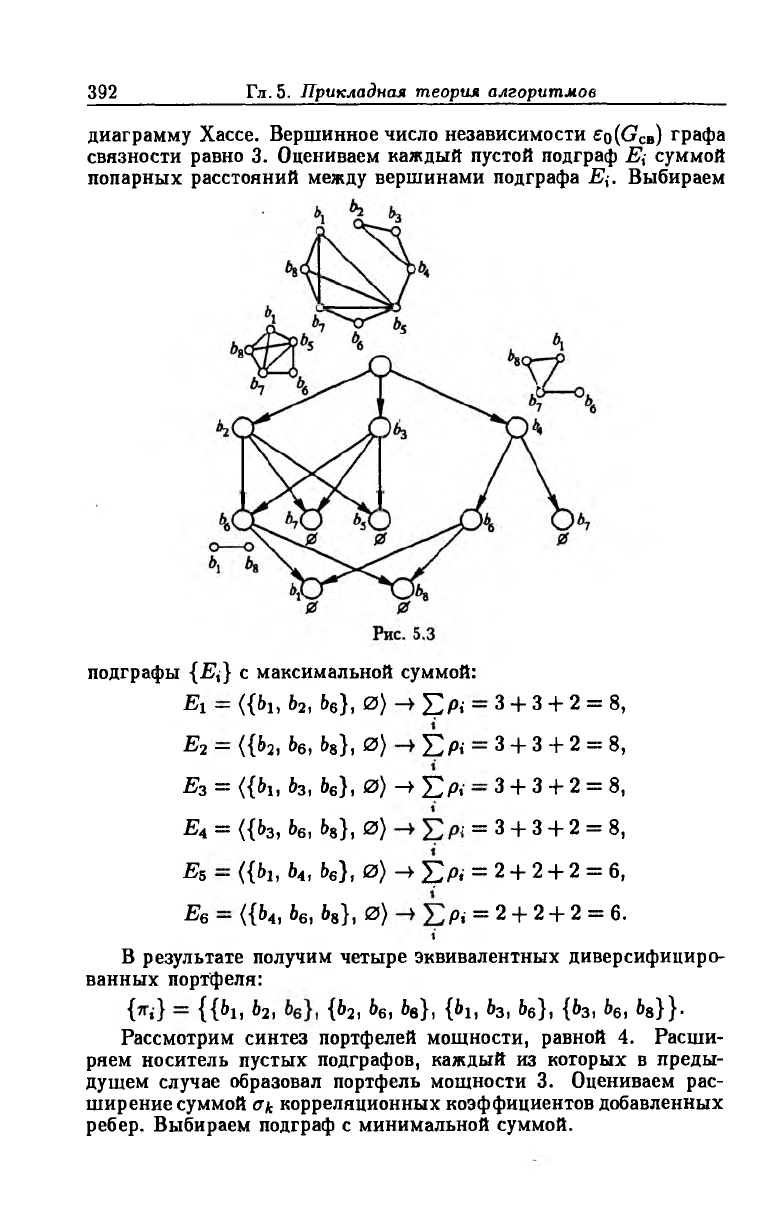
Синтезируем портфели мощности 3. Порождаем пустые под

графы графа связности GCB- На рис. 5.3 дерево естественным обра

зом преобразовано в эквивалентную в смысле включения путей

392

Гл. 5. Прикладная теория алгоритмов

диаграмму Хассе. Вершинное число независимости £о(С?св) графа

связности равно 3. Оцениваем каждый пустой подграф Е{ суммой

попарных расстояний между вершинами подграфа Е\. Выбираем

подграфы {£,} с максимальной суммой:

Е\ — <{Ьь hi &б}) 0) Y^Pi ~ 3 + 3 + 2 = 8,

Ег — ({&2i be, be}i 0 ) J2Pi — 3 + 3 + 2 = 8,

Ез = {{b\, Ьз, &б}) 0 ) —* Y2 Pi — 3 + 3 + 2 = 8,

Е* = ({&з, i>6, be}i 0 ) = 3 -f 3 + 2 = 8,

Еь — ({&i> b4, be}, 0) —> ]Cp* = 2 + 2 + 2 = 6,

Ее — ({b4, &6i &e}i 0 ) Pi = 2 + 2 + 2 = 6.

В результате получим четыре эквивалентных диверсифициро

ванных портфеля:

{*«} “ {{^ii ^2i {Ь2, 6б, b6}, {&1, Ь3, 66}, {Ь3, b6, Ьв}}-

Рассмотрим синтез портфелей мощности, равной 4. Расши

ряем носитель пустых подграфов, каждый из которых в преды

дущем случае образовал портфель мощности 3. Оцениваем рас

ширение суммой ak корреляционных коэффициентов добавленных

ребер. Выбираем подграф с минимальной суммой.

§5.1. Принципы характеризационного анализа

393

Подграф Ei расширяется вершиной Ъу\ при этом сумма сг* =

= 0,6. Добавилось ребро {i>6, ^7}, остальные расширения уве

личивают значение о>. В результате получили первый портфель

я-i = {i>i, £>2i be, &т}- Аналогично расширяем остальные 3 порт

феля; в результате получаем еще 4 портфеля с суммой <7* = 0,6:

Добиться максимального быстродействия комбинированных

алгоритмов без порождения всех эквивалентных решений, т. е. ис

пользовать малый объем памяти, позволяют алгоритмы третьего

класса, реализующие семантическое эквивалентирование.

При семантическом эквивалентировании известна не только

полная система аксиом, но и конструктивный критерий, который

позволяет:

для задачи анализа проверить истинность предиката

р ч _ ( 1, если модель Фа обладает заданным свойством,

°' ~ 1.0 в противном случае;

для задачи синтеза связать две различные абстракции — мо

дели Фа и Фь — в единую систему с помощью предиката функцио

нальной целостности

Общее, что характеризует модели Фа и Фь и что отличает их от

других, — это смысл преобразования Фа -+ Фь. Суть преобразова

ния Фа Фь — это свойство языковых выражений, инвариант

ное относительно их модельных представлений. Изучением смы

сла занимается логическая семантика, которая является разделом

металогики. Под семантикой, как правило, понимают дескрип

тивную (описательную) семантику, изучающую связь между зна-

косочетаниями формализованного языка и их интерпретациями

(толкованиями) в терминах той системы понятий, формализацией

которых является, данный язык. Здесь под семантикой понимают

изучение интерпретации одного формализованного языка в катего

риях другого, причем оба языка являются формализацией одного

и того же объекта (явления). Этот вид семантики будем называть

проективным. В частном случае, когда оба языка совпадают и

исследуется выполнимость определенного свойства изучаемой мо

дели, проективную семантику будем называть

рефлексивной.

Рефлексивная семантика позволяет решать задачи анализа мо

делей. Проективная семантика преобразования Фа —у Фь позво

ляет вычислять экстремальное значение функционала качества ре

шения у>(Фь) и строить соответствующую оптимальную модель Фь,

7Г2 = {i>2 i &6, &7 , bg) , 7Г3 = { Ьг, Ьз, Ь4, b6},

ТГ4 = {Ьз, i>4 , i>6i ^ в}, Я"5 = {Ьз, i>6, by, i>g}.

fi>(®., ФЬ)

{

1, если преобразование Фа Фь существует

при взаимно однозначном соответствии

между элементами моделей Фа и Фь,

0 в противном случае.

394

Гл. 5. Прикладная теория алгоритмов

не строя все эквивалентные модели {Фь,}, что намного уменьшает

трудоемкость алгоритмов.

Для определения проективной семантики преобразования

Фа -»• Фь необходимо:

1) найти числовые характеристики {у,} модели Фь, однозначно

определяющие значение у>(Фь);

2) установить свойства 5(, модели Фь, при наличии которых

вычислимы {^i};

3) выявить свойства Sa модели Фа, однозначно определяющие

свойства Бь модели Фь;

4) найти числовые характеристики модели Фа, обладающей

свойствами Sa, однозначно определяющие <^(Фь).

Таким образом, наличие свойств 5а позволяет однозначно вы

числить у>(Фь) без фактического построения Ф(,.

Для нахождения рефлексивной семантики анализа модели Фа

необходимо:

1) выявить свойства 5а модели Фа, однозначно определяющие

предикат Р0(Фа);

2) найти числовые характеристики модели Фа, определяющие

наличие свойств Sa-

В обоих случаях основным моментом является установление

свойств Sa модели Фа. которые определяют истинность предиката

Р0(Фа) или Ро(Фа) Фь)- Эти свойства модели Фа будем определять

отсутствием запрещенных фигур, образующих основу критерия

выполнения свойств 5а. Знание запрещенных фигур позволяет

эффективно решать задачи анализа и конструктивно вычислять

функционал у>(Фь) без генерации всех эквивалентных моделей

{Фь,} (см. рис. 5.1, в) при решении задач синтеза. Поиск про

ективных и рефлексивных семантик, основой которых являются

запрещенные фигуры, и их изучение отнесем к разделу метало

гики и будем называть конструктивной семантикой.

Взаимоотношение всех трех семантик преобразования иллю

стрирует рис. 5.4.

Рефлексивные семантики

Рис. 5.4

§5.1. Принципы характеризационного анализа

395

Проблему поиска запрещенных фигур называют характери-

зационной проблемой. Эта проблема определяется классом рас

сматриваемых моделей Ка = {Фа} и характеризуется свойством

5а, определяющим предикат Ро(Фа) или Ро(Фа, Фь)- Для реше

ния характеризационной проблемы требуется определить множе

ство запрещенных фигур К3 = {Ф,}, т. е. таких моделей Ф,,

отсутствие которых в данной модели Фа € Ка является необходи

мым и достаточным условием того, что Фа обладает свойством 5а,

и при этом никакая из моделей Ф, € К3 не присутствует в другой

запрещенной фигуре — модели Ф_, € К3.

Формализуем понятие отсутствия и присутствия одной мо

дели в другой. На множестве моделей Ка можно задать отношение

упорядочения Рп такое, что (Ф,-, Ф_,) € РП, если Ф,- присутствует

в Ф_, . Отношение Р„ называется отношением подчинения, а мо

дель Ф,- — подчиненной модели Ф_,. Отношение подчинения моде

лей служит обобщением известного отношения быть подмоделью.

Модель Ф,- является подмоделью модели Фj, если получена из Ф_,

удалением некоторых элементов носителя и/или сигнатуры. Ха-

рактеризационная проблема с заданным отношением подчинения

Рп в классе моделей определяет характеризационные задачи. По

скольку в классе моделей Ка может быть задано много отношений

упорядочения, характеризационную проблему можно рассматри

вать как целое множество характеризационных задач, каждая из

которых имеет собственное решение в виде множества запрещен

ных фигур.

От выбора отношения подчинения в решении характеризаци

онной задачи зависит многое: и компактность множества запре

щенных фигур, й разрешимость этой задачи вообще. Принци

пиальным является тот факт, что характеризационная проблема

всегда разрешима. Нужно только правильно выбрать отношение

подчинения и соответственно получить постановку разрешимой

характеризационной задачи. Покажем, каким должно быть отно

шение подчинения.

Теорема 5.1 (принцип локальности). Множество запре

щенных фигур К3 = {Ф3,} для класса моделей Ка = {Фа} с от

ношением подчинения РП и свойством 5а существует (харак

теризационная задача разрешима) тогда и только тогда,

когда справедливо, что всякая модель Ф,-, подчиненная модели

Ф^-, обладающей свойством 5а, также обладает им.

Доказательство. Допустим, что множество запрещенных

фигур существует. Тогда по определению запрещенной фигуры

никакая модель Фа, обладающая свойством 5а, не имеет запре

щенной фигуры в качестве подчиненной.

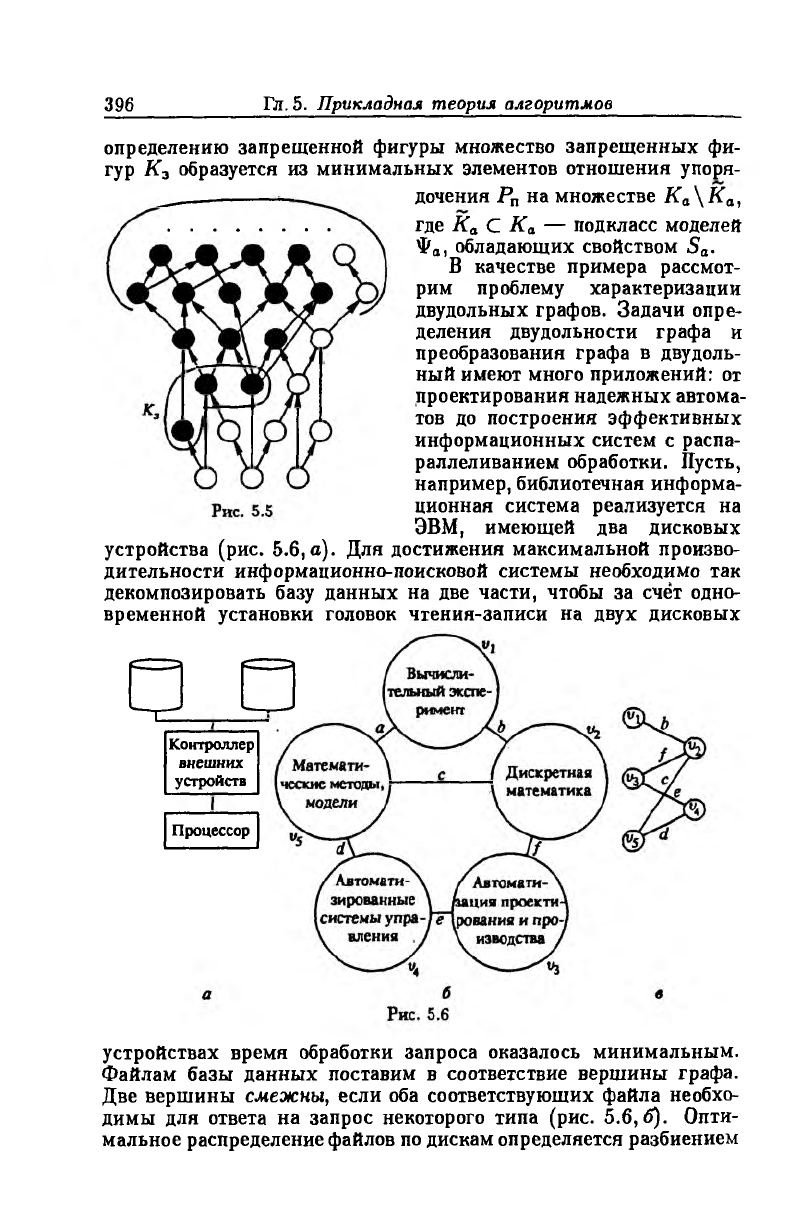
С другой стороны, пусть отношение подчинения таково, что

моделям Фа, которым присуще свойство 5а, подчинены только мо

дели, которые им также обладают (рис. 5.5). В этом случае по

396

Гл. 5. Прикладная теория алгоритмов

определению запрещенной фигуры множество запрещенных фи

гур К3 образуется из минимальных элементов отношения упоря

дочения Рп на множестве Ка\Ка,

где Ка С Ка — подкласс моделей

Фа, обладающих свойством Sa.

В качестве примера рассмот

рим проблему характеризации

двудольных графов. Задачи опре

деления двудольности графа и

преобразования графа в двудоль

ный имеют много приложений: от

проектирования надежных автома

тов до построения эффективных

информационных систем с распа

раллеливанием обработки. Пусть,

например, библиотечная информа

ционная система реализуется на

ЭВМ, имеющей два дисковых

устройства (рис. 5.6, а). Для достижения максимальной произво

дительности информационно-поисковой системы необходимо так

декомпозировать базу данных на две части, чтобы за счёт одно

временной установки головок чтения-записи на двух дисковых

Контроллер

внешних

устройств

Процессор

устройствах время обработки запроса оказалось минимальным.

Файлам базы данных поставим в соответствие вершины графа.

Две вершины смежны, если оба соответствующих файла необхо

димы для ответа на запрос некоторого типа (рис. 5.6,6). Опти

мальное распределение файлов по дискам определяется разбиением

§5.1. Принципы характеризационного анализа

397

множества вершин графа на два множества, внутри которых как

можно меньше ребер (что соответствует достижению максималь

ного параллелизма). Эта задача сводится к выявлению проектив

ной семантики преобразования графов в двудольные с минималь

ным удалением ребер. Семантику определяет решение характери-

зационной проблемы двудольности графов (рис. 5.6, в).

Класс Ка состоит из моделей, сигнатура которых образуется од

ним бинарным симметричным, антирефлексивным отношением.

Свойство Sa означает быть двудольным. Исследуем два отноше

ния подчинения: Р„ — быть частичным подграфом и Р% —

быть сводимым графом. Сводимым называется граф Ga, полу

чающийся из Gb в результате последовательного склеивания смеж

ных вершин (объединения их в одну) с соответствующим объеди

нением их окрестностей. Оба отношения удовлетворяют принципу

локальности. Следовательно, в обоих случаях характеризацион-

ная задача разрешима. Диаграммы отношения подчинения при

ведены на рис. 5.7. В случае отношения подчинения Р* множе-

Рис. 5.7

ством запрещенных фигур является множество нечетных циклов,

в случае отношения подчинения Р% — множество полных графов

порядка > 2.

Итак, всегда можио решить характеризационную проблему, а

следовательно, получить множество запрещенных фигур. Это мно

жество определяет конструктивный семантический критерий для

решения задачи анализа. Более того, знание множества запре

щенных фигур используется в методе семантического эквивален-

тирования в задачах синтеза. Основополагающим принципом се

мантического эквивалентирования является то, что знание кон

кретных запрещенных моделей, присутствующих в модели Фа и

мешающих ей обладать свойством 5а, позволяет определить те

локальные структуры, преобразование которых необходимо для

того, чтобы получить модель Фа, которой присуще свойство 5а.

При этом осуществляется только минимальный (неизбежный) пе

ребор вариантов преобразований, т. е. вычислительный процесс в

смысле трудоемкости улучшить нельзя. При семантическом экви-

398

Гл. 5- Прикладная теория алгоритмов

валентировании дерево решений (см. рис. 5.1, в) состоит из двух

звезд. Первая звезда соответствует преобразованию Фа —>■ Фь,

Р0(Фа, Фь) = I, вторая — Ф0 —>• Фь. При поиске минимального

решения необходим обход всех ветвей первой звезды, во второй

звезде достаточно взять любую ветвь, так как с точки зрения ми

нимальности решения, определяемого значением у>(Фа), все ветви

второй звезды равнозначны.

Рассмотрим подробно процесс семантического эквивалентиро-

вания. Основу этого процесса составляют способы преобразова

ния запрещенных фигур в эквивалентные разрешенные. Эквива

лентность определяется смыслом преобразования Фа —>• Фь. Как

правило, способом преобразования запрещенной фигуры в разре

шенную является удаление, введение или расщепление элемента

носителя или сигнатуры либо переход к некоторой подчиненной

модели.

Для семантического эквивалентирования или преобразования

графа в двудольный существует несколько способов преобразова

ния запрещенных фигур — циклов нечетной длины. В случае ис

пользования преобразования для вложения графа в гиперкуб при

проектировании надежных автоматов запрещенная фигура пре

образуется в разрешенную введением на ребро нечетного числа

вершин (строго говоря, здесь не одно преобразование, а множе

ство). Если преобразование используется для оптимальной деком

позиции базы данных, то способ преобразования заключается в

удалении ребра. Принципиальным является то, что способ пре

образования запрещенной фигуры в разрешенную существует все

гда, когда преобразование Фа —>• Фь имеет смысл. Действительно,

для каждой модели Фа существует эквивалентная модель Фа, обла

дающая свойством 5а. Следовательно, существует преобразование

Фа в Фа, а любое преобразование модели Фа в модель, обладаю

щую свойством 5а, обязательно преобразует запрещенные фигуры

в разрешенные. Таким образом, способ преобразования запрещен

ной фигуры в разрешенную существует всегда.

В общем случае существует множество преобразований запре

щенной фигуры в разрешенную. Пусть Я, = {г,-.} — множество

способов преобразований запрещенной фигуры Ф,- £ К3 (т. е. для

всякого j г,--(Ф<) — разрешенная фигура). Построим множество

базисных способов преобразований С Ri, т. е. такое мини

мальное по включению множество г? , что для любого г,- най-

1 J

дется последовательность преобразований из R°, переводящая Ф,

в г;, (Ф,).

Рассмотрим способы преобразования запрещенных фигур для

преобразования мографа в линейный, что важно в задачах ор

§5.1. Принципы характеризационного анализа

399

ганизации данных в информационно-поисковых системах и ба

зах данных. Основными характеристиками размещения данных

в памяти являются объем занимаемой памяти и время доступа.

При представлении информационно-поисковой системы мографом

объем памяти определяется мощностью носителя, а время дос

тупа — временем считывания слов модели. Одним из способов

оптимальной организации данных в памяти является линейное

размещение, которое предполагает такое линейное (полное) упо

рядочение объектов данных, что ответ на каждый вопрос есть це

почка непосредственно следующих в этом упорядочении объектов

данных. Поставим в соответствие объектам данных элементы но

сителя мографа, ответам на запросы — слова. Мограф называется

линейным, если допускает линейное размещение элементов носи

теля, при котором все слова представляются цепочками. Таким

образом, для получения оптимальной организации данных необхо

димо преобразовать мограф в линейный и, следовательно, решить

характеризационную проблему линейности мографа.

Не конкретизируя вид запрещенных фигур (этот вопрос по

дробно рассмотрен далее), отметим, что возможны два способа

преобразования запрещенных фигур в разрешенные:

1) расщепление элемента носителя х на х и х' с соответст

вующей заменой х на х' в некоторых словах, в которые входил

элемент х;

2) расщепление слова М, т. е. замена его на два слова.

Можно показать, что эти способы образуют базисное множество

способов преобразований запрещенных фигур в разрешенные.

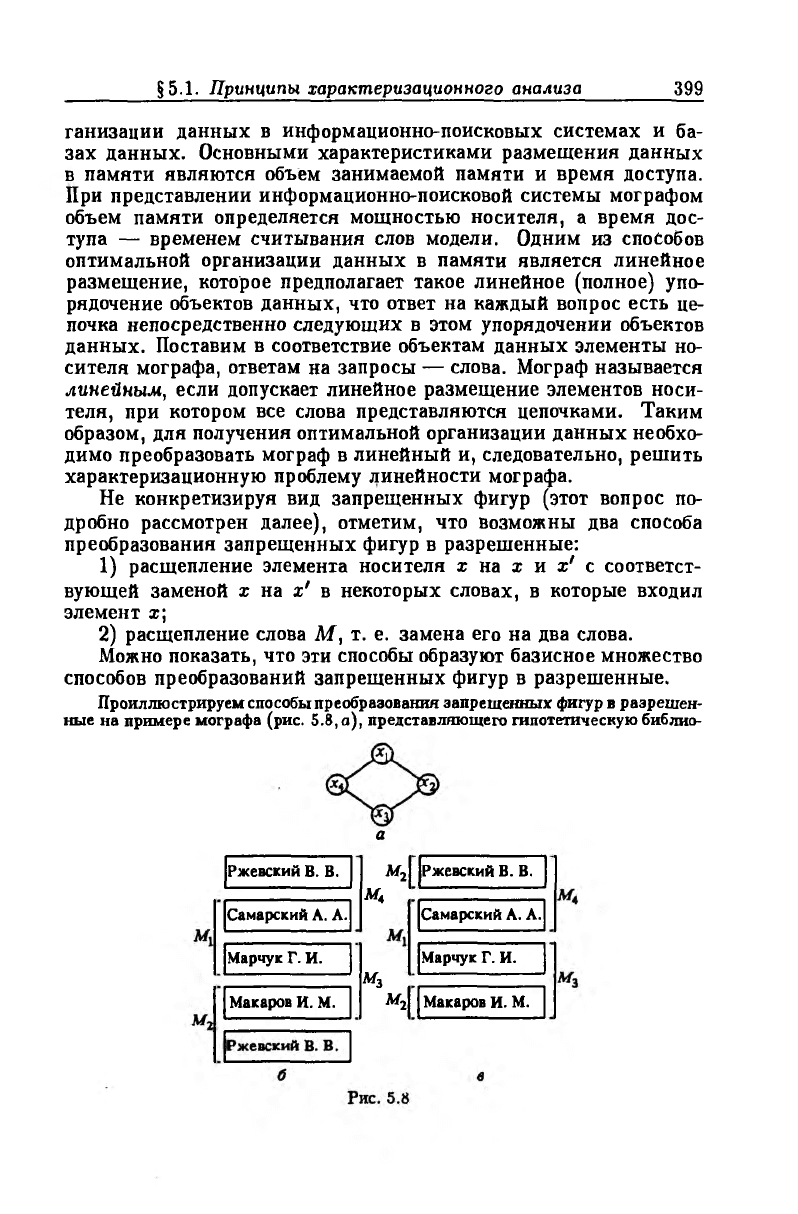
Проиллюстрируем способы преобразования запрещенных фигур в разрешен

ные на примере мографа (рис. 5.8, а), представляющего гипотетическую библио-

Ржевский В. В.

м 2

Ржевский В. В.

М4

Самарский А. А.

Марчук Г. И.

Макаров И. М.

м 2

Макаров И. М.

400

Гл. 5. Прикладная теория алгоритмов

темную информационную систему, включающую информацию о следующих кни

гах:

xi — Ржевский В.В. Процессы открытых горных работ. — М.: Недра,

1978;

х2 — Самарский А.А. Теория разностных схем. — М.: Наука, 1977;

хз — Марчук Г.И. Методы вычислительной математики. — М.: Наука,

1977;

Х4 — Оснокы автоматизации управления производством / Под ред. Мака

рова И.М. — М.: Высшая швола, 1983.

В ней реализуются следующие запросы:

М\ — Книги по вычислительным методам. Ответ {х2, х3};

Мг — Книги по автоматизации процессов. Ответ {xi, х4};

Мз — Книги авторов (редакторов), фамилии которых начинаются с букв от

А до М. Ответ {хз, х<};

Mi — Книги авторов (редакторов), фамилии которых начинаются с букв от

Н до Я. Ответ {xi, хг}.

Данный мограф не является линейным. Можно показать, что каждый эле

мент носителя и каждое слово входят в запрещенную фигуру. Расщепление

элемента носителя или слова должно преобразовать мограф в линейный. Рас

смотрим, например, расщепление элемента x i. Преобразованный мограф явля

ется линейным и представляется линейно упорядоченным, приведенным на

рис. 5.8,6. При расщеплении любого слова, например, Мг, мограф также ста

новится линейным и представляется линейно упорядоченным, приведенным на

рис. 5.8,в. В первом случае увеличивается объем памяти, занимаемый объек

тами данных, во втором — увеличивается среднее время ответа на запросы.

Каждый способ преобразования г,- характеризуется стои

мостью ct>. Функционал качества преобразования у>(Фь) опреде

ляется стоимостью произведенных преобразований запрещенных

фигур в разрешенные.

Для выполнения преобразования Фа —> Фа неизбежно преобра

зование каждой запрещенной фигуры в разрешенную, поэтому вы

берем для каждой запрещенной фигуры Ф3| С Фа один из спо

собов ее преобразования; их совокупность определит глобальное

преобразование Фа —)• Фа. Такое преобразование в общем случае

может не достигать экстремума функционала у>(Фг>), даже если

для каждой фигуры ФЭ| выбран способ преобразования с наимень

шей стоимостью. • Это обусловлено тем, что возможен способ пре

образования Ф3,, пусть имеющий не наименьшую стоимость, но

преобразующий заодно и другую запрещенную фигуру ФЭ|. Более

того, взаимосвязь способов преобразования запрещенных фигур

может оказаться очень сложной, поэтому простой выбор способов

преобразования по одному на каждую фигуру Ф3< С Фа не обеспе

чивает достижения экстремума функционала качества у>(Фь).

Процедура семантического эквивалентирования основана на

построении семантической таблицы. Столбцам этой таблицы соот

ветствуют запрещенные фигуры,, присутствующие в модели, стро

кам — компоненты запрещенных фигур. Элемент (г, j ) таблицы

равен 1, если преобразование t-й компоненты превращает j-ю за

прещенную фигуру в разрешенную, и 0 в противном случае. По