Горбатов В.А. Фундаментальные Основы Дискретной Математики. Информационная Математика

Подождите немного. Документ загружается.

§5.6. Семантическое ослабление функциональной связности 451

{1.4}

{4,5}

{3. 4}

Аналогично, рассматривая остальные сцепленные лары вну

тренних состояний, получаем граф Gp (рис. 5.38, а), показываю

щий условия соцветности сцеп

ленных состояний. В этом гра-

-------

J3! 5}

фе каждая вершина взаимно

однозначно соответствует паре

сцепленных состояний, кото

рая играет роль веса соответ

ствующей вершины, дуги графа

показывают условия соцветнос

ти сцепленных пар. Отношение

соцветности обладает свойством

транзитивности. Расширим

сигнатуру этого графа добавле

нием транзитивно замыкаю

щих дуг. Согласно свойству транзитивности полученный граф в

дальнейшем будем называть графом расцепления. Условия, при

которых сцепленные вершины могут быть окрашены в один цвет,

определяются следующим утверждением.

Утверж дение. Если вершина и(5,-, Sj) графа расцепления

соединена путем с полным подграфом, объединение весов вер

шин которого равно носителю графа сцепления, то для вершин

Si, Sj не существует условия, при котором эти вершины со-

цветны.

В рассматриваемом случае ни одна пара сцепленных вершин

не может быть соцветна, так как каждая вершина графа расцепле

ния соединена путем с вершинами {из, v4, v5, v6}, которые после

добавления транзитивно замыкающих дуг образуют полный под

граф, объединение весов вершин которого равно носителю графа

сцепления.

Производим расцепление сцепленных состояний {Si, S3} и

{S 3, S5} расширением входных векторов а и с. В результате за

данная таблица переходов автомата эквивалентируется табл. 5.28.

Матрица смежности (см. табл. 5.22) преобразуется в матрицу

смежности, представленную в табл. 5.29.

Таблица 5.28 Таблица 5.29

a,b a,b

a,b

a, с a,b

a, с a, с

a,b a, с

a,b

a, b a,b

Si Si

Si S3

с' Si

с"

452

Гл. 5. Прикладная теория алгоритмов

После удаления ребер {Si, S3} и {S3, S5} хроматическое число

графа сцепления равно 2:

K0 = {Si, S3, S5}, Кх = {S2,S4}.

Соединяя соцветные вершины ребром, получаем граф сцепле

ния для определения значений второго разряда кодов внутрен

них состояний. Граф сцепления для второго разряда представ

ляет собой полный граф на пяти вершинах {Si, S2, S3, S4, S5}.

Этот граф содержит запрещенные фигуры фЖ|- — циклы нечетной

длины:

Cl = {{Si, S2}, {S2, S3}, {S3, S4}, {S4, Ss}, {Si, S5}},

c 2 = {{Si, S3}, {S3, Ss}, {S2, Ss}, {S2, S4}, {Si, S4}},

Сз = { { S i,S 2},{S 2,S 3}, {S i,S 3}},

C4 = {{S2, S3}, {S3, S4}, {S2, S4}},

Cs = {{S3, S4}, {S4, Ss}, {S3, s5}},

C6 = {{S i, S4}, {Si, Ss}, {S4, S5}},

c 7 = {{S i,S 2}, {S b S5}, {S 2,S 5}},

c B = {{S i, S2}, {Si, S4}, {S 2, S4}},

c 9 = { { S2, S3}, {S2, Ss}, {S 3, Ss}},

C io = {{S i,S 3}, {S i,S 4}, { S3,S 4}},

Cn = { { S2, S4}, {S2, Ss}, {S4, S5}},

Ci2 = {{Si, S3}, {Si, Ss}, {S3, S5}}.

Семантическая таблица — табл. 5.30.

Таблица 5.30

Cs Ce C T Cg c9

Сю

Cn C i2

{S i,S 2}

1 1 1

to , S3}

1 1

{Si,S<} 1 1 1

{S i,S 5}

{S2 )s 3}

1 1

{S2 ,S 4} 1

1 1

{S2 ts s} 1

1 1

{S3 ,S 4 } 1 1 1 1

{S3, Ss}

1 , 1 1

{S«, S5)

Очевидно, что граф расцепления, соответствующий второму

разряду, получается из графа расцепления первого разряда путем

удаления вершин, взвешенных расцепленными состояниями, и

инцидентных им дуг. После удаления вершин t>i и v2 получаем,

§ 5.6. Семантическое ослабление функциональной связности 453

что ни одна пара сцепленных вершин не может быть соцветна.

Поэтому расцепление пар {Si, S2}, {S 2, S5}, {S 3, S4}, вошедших

в минимальное покрытие {{S i, S2}, {Si, S5}, {S2, S5}, {S3, S4} }

табл. 5.30, производим расширением входных векторов а, Ь, с.

После удаления ребер {Si, S2}, {Si, S5}, {S 2, S5}, {S3, S4},

вошедших в покрытие, раскрашиваем граф сцепления в две кра

ски:

К0 = {Si, S2, S5}, К\ = {S3, S4}.

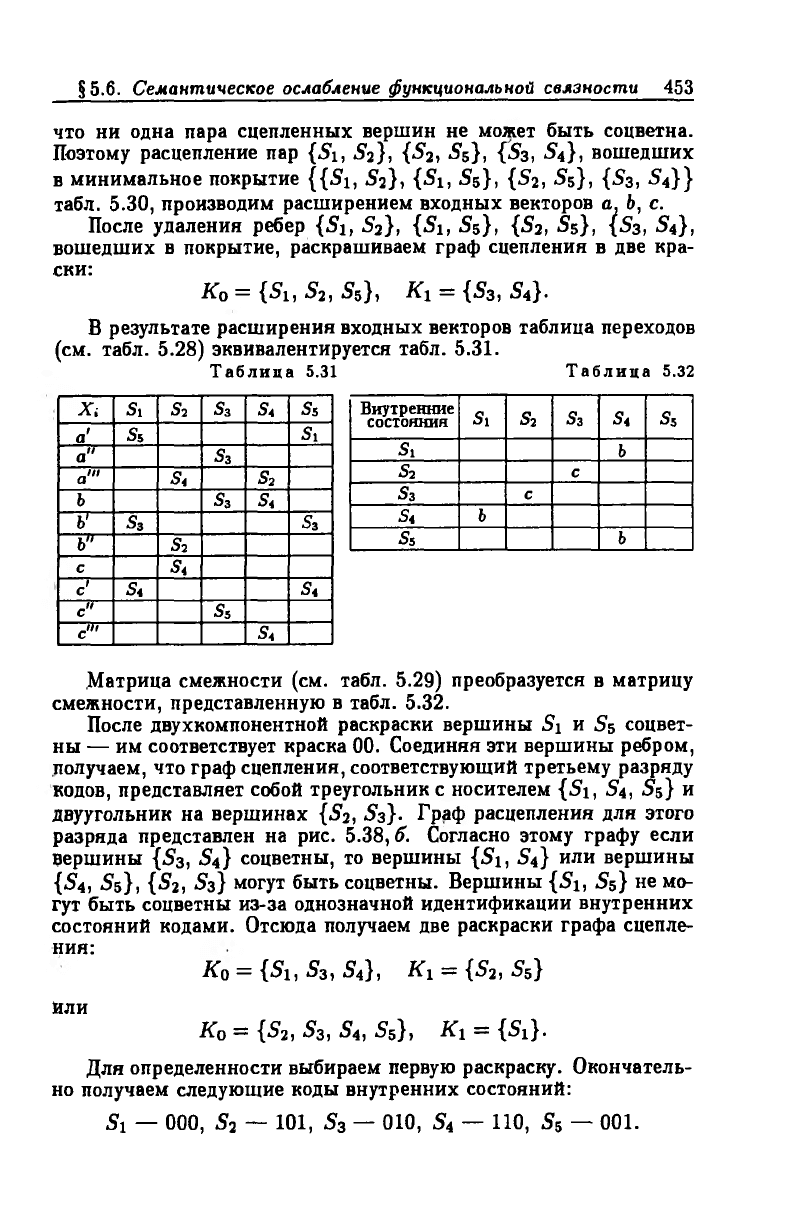
В результате расширения входных векторов таблица переходов

(см. табл. 5.28) эквивалентируется табл. 5.31.

Таблица 5.31 Таблица 5.32

Внутренние

состояния

S i

s 2 s 3

S i b

S 3

Ss b

Si S2 S 3

a "

S 3

a"'

s 2

S 3

с' Si s<

с"

сш

.Матрица смежности (см. табл. 5.29) преобразуется в матрицу

смежности, представленную в табл. 5.32.

После двухкомпонентной раскраски вершины Si и 5s соцвет-

ны — им соответствует краска 00. Соединяя эти вершины ребром,

получаем, что граф сцепления, соответствующий третьему разряду

кодов, представляет собой треугольник с носителем {Si, S4, S5} и

двуугольник на вершинах {S 2, S3}. Граф расцепления для этого

разряда представлен на рис. 5.38,6. Согласно этому графу если

вершины {S3, S4} соцветны, то вершины {Si, S4} или вершины

{S 4, S5}, {S 2, S3} могут быть соцветны. Вершины {Si, S5} не мо

гут быть соцветны из-за однозначной идентификации внутренних

состояний кодами. Отсюда получаем две раскраски графа сцепле

ния:

Ко = {Si, S3, S4}, К г = {S 2, S5}

Или

Ко = {S 2, S3, S4, S5}, К\ = {S i}.

Для определенности выбираем первую раскраску. Окончатель

но получаем следующие коды внутренних состояний:

Si — ООО, S2 — 101, S3 — 010, S4 — НО, S5 — 001.

454

Гл. 5. Прикладная теория алгоритмов

После замены штрихов у входных векторов а, Ь, с соответствую

щим расширением этих векторов внутренними переменными по

лучаем условия переходов элементов памяти, представленные в

табл. 5.33.

Таблица 5.33

0 1 0

1 0

i = 1 i = 2

1 = 3

a VbV

Vcz*

С*7

02j+ V

V62+

azfv

Vbzf V с

02 j+ z} V bV

Vc(21+2j+V

V2+2+)

a(z+ 0z+)V

Vczfzf

a VbV с azfv

VC2j+

dzf V bV

VC2j+

a V bz / V с

bzf

Функционал <p(G), как и в предыдущем решении, равен 4.

§ 5.7. Решение проблемы повторной

функциональной декомпозиции в булевой логике

В гл. 2 (§2.2) было введено понятие функциональной деком

позиции. Рассмотрим проблему синтеза функциональной деком

позиции для общего случая, когда переменные, соответствующие

строкам и столбцам, в матрице Вейча пересекаются. Представим

заданное булево пространство Р (Х ) в виде декартова произведения

Р(Х а) х Р{ХЬ) пространств Р (Х а), Р (Х Ь), {Х а} U (Х ь) = {X },

{Х а} П {Хь) = 0 .

Каждой точке пространства Р(Х а) взаимо однозначно сопоста

вим вершину € Va графа Ga = (V^,0 ), а точке пространства

Р(Хь) — вершину Vb G И графа Gb = (И, 0)- Тогда граф

G = (VaUVb, Uu Щ , G = Ga + Gb,

определит исходное пространство Р(Х ). При этом если булева

функция f(X ) в этом пространстве принимает единичное значе

ние в точке Xi, то вершины vai € Va и € И, соответствующие

этой точке, соединены неинверсным ребром {vai, иь,} € U\\ если

f{X ) принимает нулевое значение, то вершины vai и vbt соеди

нены инверсным ребром {uai, vj,.} € Uq] если же функция f(X ) в

точке Xi = Х а{ Хь, (вектор Xi есть результат конкатенации век

торов X ai и Хь{) не определена, то {иа,, иг>,} £ U\, Uq. Получен

ный граф K (f) является графом Кёнига и имеет два сорта ребер:

неинверсные и инверсные. Очевидно, что каждая вершина va. € Va

взаимно однозначно соответствует остаточной булевой функции

/(и,,, оа2, ...,<так, Х ь), а вершина vbi € Vy— остаточной функции

/(Х а, °ь{к+1), сть(к+2), ..., сть„) в разложении Шеннона по строчным

§ 5.7. Решение проблемы повторной декомпозиции 455

и столбцевым переменным соответственно:

f{Xa,X b)=V к\х?-/№,Хь), Е,»<Та1<Таз...<Так,

f(X a, Хь) = ' 'f(X a, Ej), Ej Gbk+iGbk+i • • •O'bn-

Рассмотрим, например, булеву функцию

fix, X, а: . ! - / 1 на 0,1,4,17,18,26,30,

Д*1, *2, на 2,3,11,19,29.

В качестве Х а выберем переменные xi: х2; в качестве Хь — пе

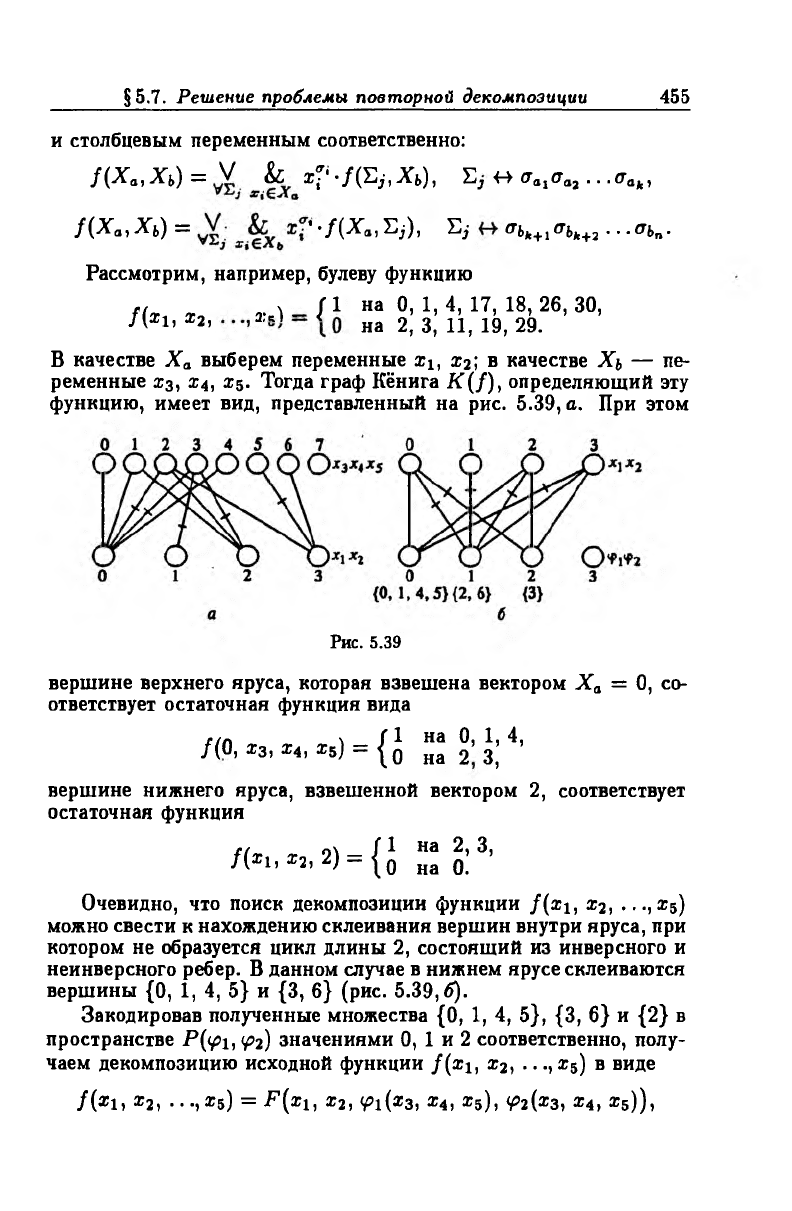
ременные хз, а?4, Х5. Тогда граф Кёнига K (f), определяющий эту

функцию, имеет вид, представленный на рис. 5.39, а. При этом

Рис. 5.39

вершине верхнего яруса, которая взвешена вектором Х а = 0, со

ответствует остаточная функция вида

_ Г1 на 0, 1, 4,

/(0, 1 3, 1 4, х5) - | 0 на 2’ 3|

вершине нижнего яруса, взвешенной вектором 2, соответствует

остаточная функция

г/ п\ f 1 на 2, 3,

f(x 1, 1 2, 2) = |( ’ ’

.0 на 0.

Очевидно, что поиск декомпозиции функции f(x i, х2, • • •, *б)

можно свести к нахождению склеивания вершин внутри яруса, при

котором не образуется цикл длины 2, состоящий из инверсного и

неинверсного ребер. В данном случае в нижнем ярусе склеиваются

вершины {0, 1, 4, 5} и {3, 6} (рис. 5.39,6).

Закодировав полученные множества {0, 1, 4, 5}, {3, 6} и {2 } в

пространстве P(<pi, <рг) значениями 0, 1 и 2 соответственно, полу

чаем декомпозицию исходной функции f(x i, х2, .. ., х5) в виде

/(х 1, х2, ..., х5) = F (x i, х2, <fii(x3, х4, х5), <р2(х3, х4, х5)),

456

Гл. 5. Прикладная теория алгоритмов

где

ч Г1 на 0, 8, 10, 13, 14,

, х2, v?i, (ft) - (о на 2, 5, 9, 12,

<Pi(x3, х4, хв) = { J J® q’ 3) 4) 5) б)

, ч /1 на 3, 6,

9г(*з, *4, *5) - | 0 на о, 1 , 2, 4, 5.

Для поиска объективных причин, определяющих декомпози

цию булевых функций в общем случае, предложим теоретико-гра

фовую интерпретацию этой задачи.

Для построения декомпозиции функции /(X ) определим поня

тие графа противоречивости.

Строчным графом противоречивости Gnp(Xa) — (Va, Unp),

называется граф, каждая вершина V,- которого взаимно однозначно

соответствует вектору :

{*„.-} О К , ипр с К2,

R ,, «.>} € tf„P ^ (3xbj){f(xia, хЬ}) ф /(*,•„, Хь,)).

Столбцевым графом противоречивости Gnp(Xb) = (Vj,, J7np)

называется граф, каждая вершина Vj которого взаимно однозначно

соответствует вектору X bj:

{X bj} » V b, ипр С vb2,

К , , € ипр f* (3Xai)(f(X ai, X j.) Ф f(X a„ Xj,)).

Названия графов противоречивости Gnp(Xa) и Gnp(Xь) соот

ветственно «строчной» и «столбцевой» указывают на возможность

задания графа Кёнига K (f) — (Va U Vb', U\, Uq), определяющего

булеву функцию f(x i, x2, •.., xn), в виде соответствующей двумер

ной таблицы Вейча, в которой каждая строка (столбец) задает со

ответствующую остаточную функцию в разложении Шеннона.

Теорем а 5.7 (А.В.Горбатов). Булева функция f(X ) деком

позируема в виде F((pi(Xa), <Рг(Ха), ..., <рь(Ха), Хь) тогда и

только тогда, когда ближайшее большее целое двоичного ло

гарифма хроматического числа h(G„Р(Ха)) графа противоре

чивости <?„р(Ха) = (Va, и„р) меньше |ЛТ„|:

f(X ) = F {^ (X a), M X *), --.М Х а ), Хь) »

[logaM Gnp^.))] <|Хв|, (5.3)

где k = [log2 Л(Спр(Х а))], [ ] — знак ближайшего большого це

лого.

§ 5.7. Решение проблемы повторной декомпозиции 457

Рассмотрим функцию

,, ч _ / 1 на 1,4,9,11,13,14,17,19,20,28,

/ (*!, х2, ..., х5) - { 0 на 0) б) 12) 15) 1б) 18) 22) 23 24) 2б) 29

Граф Кёнига, соответствующий разложению заданного простран

ства

Р{х 1, х2, . . ж5) = Р(х 1, х2, х3) х Р(х4, х5),

имеет вид, представленный на рис. 5.40.

Построим граф противоречивости для строчных остаточных

функций Gnp(Xa) (рис. 5.41, а); при его построении учитываем,

что две вершины, u,(Xaj) и Uj(Xa>), {u,(Xai), Vj(Xa, )} € Unp,

смежны, если найдется вершина Vk(Xb) другого яруса, которая

соединена с вершиной и,(Ха.) неинверсным ребром, а с вершиной

Vj(Xaj) — инверсным (рис. 5.41, б). Граф Gnp(Xa) содержит ква

зиполный подграф Q(3, 0):

V{Q(3, 0)) = {1, 3, 4}.

Согласно характеризационному анализу минимальное число

красок равно трем:

a = {0,2, 4, 6}, Ь= {1 ,5 ,7 }, с = {3 }.

Теорема 5.7 справедлива. После кодирования красок с помо

щью символов <pi<p2 (a — 00, b — 01, с — 10) получаем декомпо

зицию заданной функции /(хi, х2, ..., х$) вида

/ (*1, хг, • • •, *5) = * 2, Х3), <p2(xi, х2, х3), i 4, х5),

V>i(xi, х2, х3)

(fi2(xt, х2, х3)

= V(3),

= V(l, 5, 7).

Функция F(<pi, <р2, *4, xg) . определяется матрицей Вейча

{табл. 5.34), полученной в результате соответствующего раскраске-

458

Гл. 5. Прикладная теория алгоритмов

склеиванию строк матрицы Вейча, определяемой по выбранному

Таблица 5.34

________________________

Таблица 5.35

*1 *2 *3

*4 *5

2 3

0 0 1

1 1 0

0 1 1 0

0 1 0 1

5 1

0 0

7 1 0

¥>1¥>2

*4 *5

0 1 2

0 0 1

0 1

1 0

2 0

1 1 0

разложению пространства Р(хi, х2, •••,*5) (табл. 5.35):

ч / 1 на 1, 3, 4, 9, 10,

F{<pi, у?2, х4, х5) - | о на 0; 2; 5) б; 8; п

В дальнейшем функции <р\, <р2 будем называть внутренними,

а функцию F — внешней; множества переменных, вошедших в

различные сомножители при разложении заданного пространства,

назовем взаимно дополняющими до полного множества.

В рассматриваемом случае множества Ха = {xi, х2, хз) и Хь =

= {х 4, xs} являются взаимно дополняющими друг друга до пол

ного множества X = {* i, х2, • • •, х$}.

Очевидно, что условия декомпозируемости по столбцевым пе

ременным будут аналогичными (5.3).

Булева функция f(X ) декомпозируема в виде

f(X) = F{Xa, т(Хь), V2(Xb),...,Vs(Xb))

тогда и только тогда, когда [lo g2h{G пр №>))] < 1*ь|:

f(X ) = F{xa, т(Хь), т(Хь) , .., п.(Хъ)) **

*+ [1о82л(с„р(а:ь))] <\Хь\, (5.4)

где s = [log2 /г(Спр(Хб))].

Рассмотрим булеву функцию

.. ч Г 1 на 0, 4, 12, 16, 17, 19, 21, 26, 30,

f(x 1, ха, ..., х5) - | о на 1; 3 5; б; 9 10; 23, 24, 28, 31.

Представим исходное пространство P (x lt х2, ..., Х5) в виде де

картова произведения пространств Р (Х а) х Р{Хь), где Х а = {xj,

х2}, Хь = {хз, х4, Х5}. Тогда получим граф Кёнига и матрицу

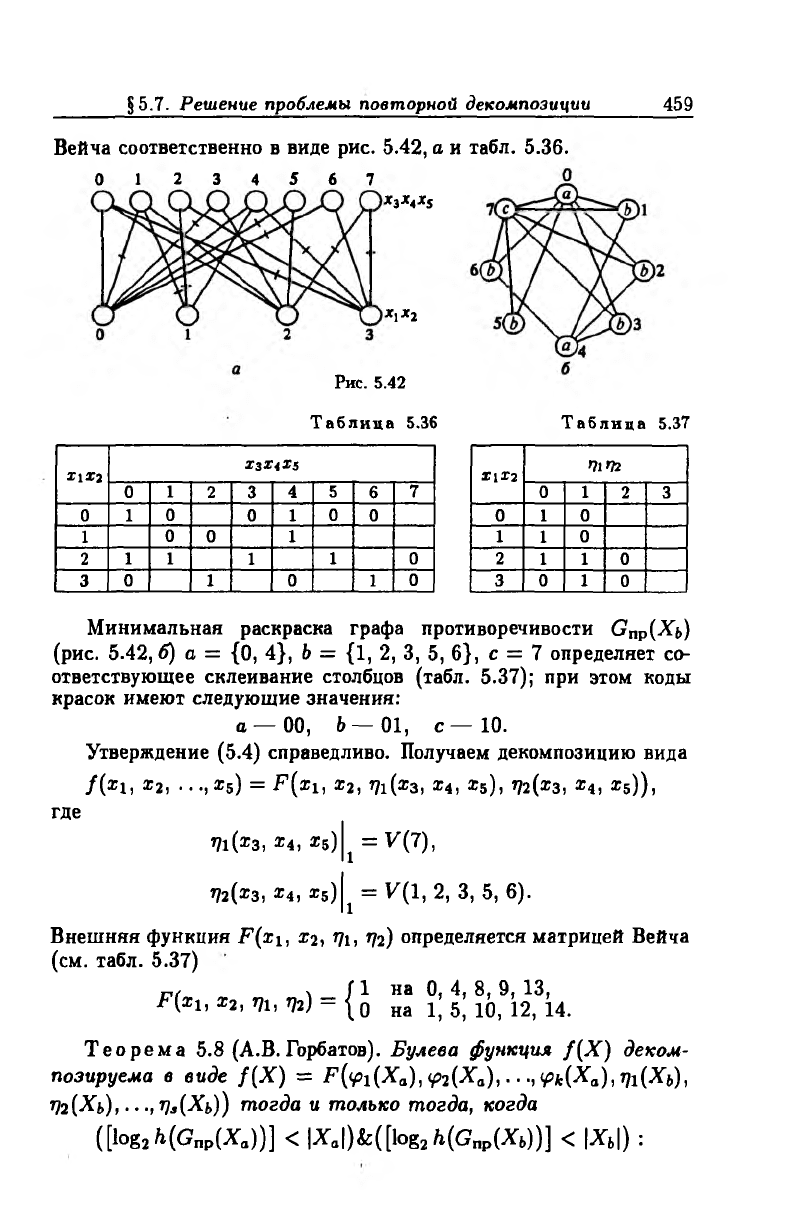
§ 5.7. Решение проблемы повторной декомпозиции

459

Вейча соответственно в виде рис. 5.42, а и табл. 5.36.

0 1 2 3 4 5 6 7

Х3Х4Х5

*1*2

Рис. 5.42

Таблица 5.36

Таблица 5.37

XI хз

X3X4 XS

0 1

2 3

4 5

0 1

2 1

0 1 0

XiX?

nim

0 1

2 з

0 1 0

1 1 0

3 0 1

Минимальная раскраска графа противоречивости Gnp(Xi>)

(рис. 5.42, б) а = {0, 4}, Ъ = {1, 2, 3, 5, 6}, с = 7 определяет со

ответствующее склеивание столбцов (табл. 5.37); при этом коды

красок имеют следующие значения:

а — 00, Ь — 01, с — 10.

Утверждение (5.4) справедливо. Получаем декомпозицию вида

/(ц , х2, ..., х5) = F(x 1, Х2, Tf\(х3, х4, х5), т)2(х3, х4, х5)),

где

r/i(x3, х4, х5) i = V(7),

т)2(х3, х4, х5) ^ = F (l, 2, 3, 5, 6).

Внешняя функция F(xi, х2, Щ, щ) определяется матрицей Вейча

(см. табл. 5.37)

, /1 на 0, 4, 8, 9, 13,

F(x1,x 2, m,r]2) = [ 0 на х; 5; хЬ, 12, 14.

Теорем а 5.8 (А.В.Горбатов). Булева функция f(X ) деком

позируема в виде f{X ) = Р(^1(Ха),^ 2(Ха),---,^(^а),»71№ ),

г)2{Хь) , ..., г?л(Хь)) тогда и только тогда, когда

([log2/i(Gnp(X a))] < |Xa|)&([log2/i(Gnp(Xb))] < \Xb\) :

460

Гл. 5. Прикладная теория алгоритмов

/(X) = F(Vl(Xa), ЫХа), . . <рк(Ха),гц(Хь),т(Хь),. . .

...МХь)) <-> ([log2fc(Gnp(Xe))] < |Ха|)&

H H 2h{Gnp(Xb))]< )X b\) (5.5)

при совместной раскраске графов Gnp(Xa) и Gnp(Xb)', при этом

Var\Vb = 0.

Рассмотрим булеву функцию

v _ /1 на 0,4,12,16,17,19,21,24,26,28,30,

*з, ..., хъ) - на 1,3,5,5,9,10,23,31.

Представление исходного пространства Р (i lt х2,.. х5) выберем

в виде

P (xlt 12, • • • > ^s) = Р(хь Х2) X Р{х3, 14, Z5).

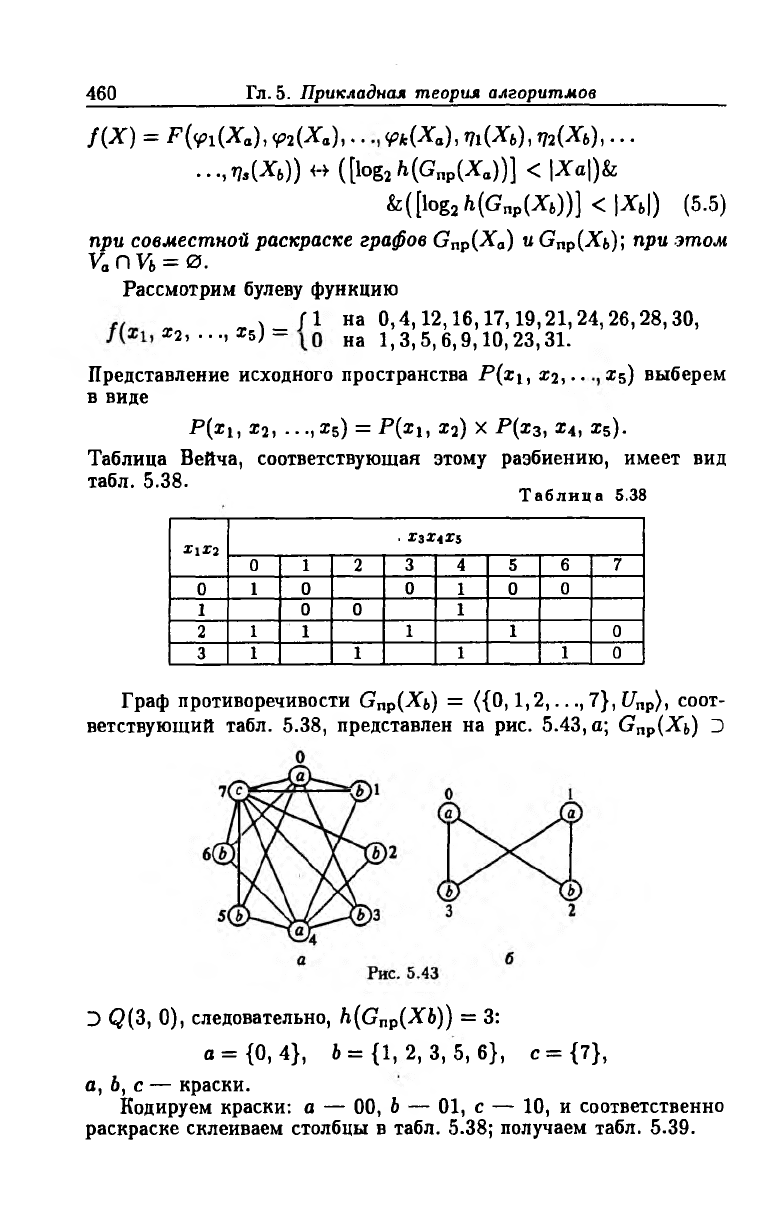
Таблица Вейча, соответствующая этому разбиению, имеет вид

табл. 5.38.

Таблица 5.38

Х\Х2

• Г3Х4Г5

0 1

3 4 5

6 7

1 0

0 0 1

1 1 0

1 1

1 1 0

Граф противоречивости Gnp(Xb) = ({0,1,2,..., 7}, С/Пр), соот

ветствующий табл. 5.38, представлен на рис. 5.43, a; Gnp(Xь) Э

Э Q{3, 0), следовательно, h(Gnp(Xb)) = 3:

а = {0,4}, Ь = {1,2, 3,5, 6}, с = {7 },

а, 6, с — краски.

Кодируем краски: а — 00, Ь — 01, с — 10, и соответственно

раскраске склеиваем столбцы в табл. 5.38; получаем табл. 5.39.