Горбатов В.А. Фундаментальные Основы Дискретной Математики. Информационная Математика

Подождите немного. Документ загружается.

§ 5.8. Синтез функциональной декомпозиции в k-знаиной логике 471

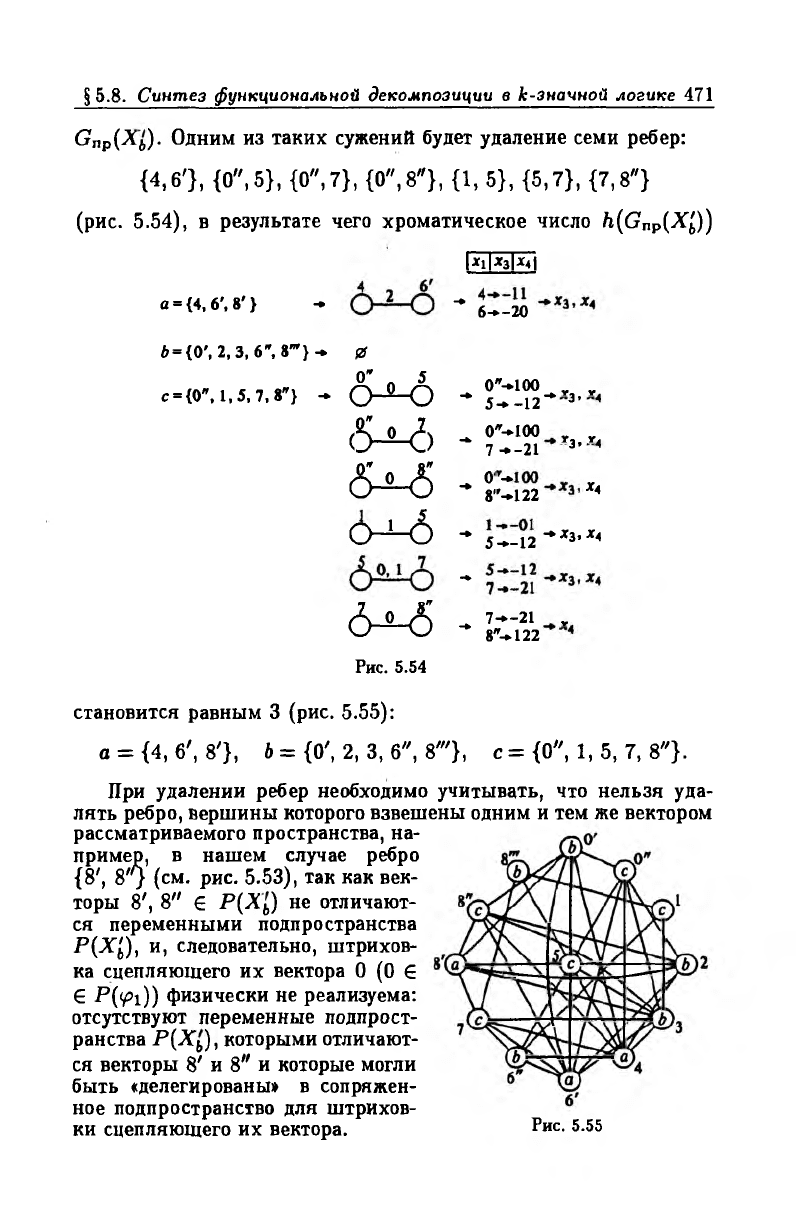
Gnp(-Xj). Одним из таких сужений будет удаление семи ребер:

{4,6'}, {0", 5}, {О", 7}, {О", 8"}, {1, 5}, {5,7}, {7,8"}

(рис. 5.54), в результате чего хроматическое число h(Gnp(X'b))

|*1|*3|*4|

в = { 4, 6', 8 '} -

- 6 - 2 0

Ь = {0', 2, 3 ,6 я, 8” } -

с = {0", 1, 5, 7, 8 "} -

0 * 5

0 - 2 - 0

0"-100 v v

- 5-* -12 ”* 3’ 4

< W >

_ 0^100 у у

7 -*-21 3’ 4

- J C m *

с и - 6

- 5— 12 - * 3’ * 4

< W 5

7-*-21 „

- 8"-* 122

Рис. 5.54

становится равным 3 (рис. 5.55):

а = {4, б', 8'}, Ъ = {O', 2, 3, б", 8'"}, с = {0", 1, 5, 7, 8"}.

При удалении ребер необходимо учитывать, что нельзя уда

лять ребро, вершины которого взвешены одним и тем же вектором

рассматриваемого пространства, на

пример, в нашем случае ребро

{ 8', 8'0 (см. рис. 5.53), так как век

торы 8', 8" 6 P(-Xt) не отличают

ся переменными подпространства

Р{Х'Ь), и, следовательно, штрихов-

ка сцепляющего их вектора 0 (0 €

G P(v>i)) физически не реализуема:

отсутствуют переменные подпрост

ранства Р (Х Ь), которыми отличают

ся векторы 8' и 8" и которые могли

быть «делегированы» в сопряжен

ное подпространство для штрихов

ки сцепляющего их вектора.

Рис. 5.55

472

Гл. 5. Прикладная теория алгоритмов

В рассматриваемом случае (см. рис. 5.54) для соцветности вер

шин 4, 6', 8' необходимо было удалить ребро {4, 6'}, для чего

расширить сопряженное подпространство P(<pi) до P(<pi, Хз) или

Р(<р 1, 14) переменной 13 или х4, которыми отличаются векторы

4 и б'. Вершины 0', 2, 3, 6", 8'" образуют пустой подграф, и уда

ления ребер не требуется. Для соцветности вершин 0 , 1, 5, 7, 8"

необходимо удалить шесть ребер При этом векторы, соответствую

щие вершинам ребер {0", 5}, {О", 7}, {0", 8"}, {1, 5}, {5, 7} от

личаются как переменной 13, так и х4. Векторы, соответствую

щие ребру {7, 8"}, отличаются переменной х4. Следовательно,

при расширении переменной х4 сопряженного подпространства

P(<Pi) —> Р(<р 1, 14) реализуема штриховка всех векторов подпро

странства P(<pi), порождающих семь удаляемых ребер в простран

стве Р{Х'Ь). Склеиваем соцветные вершины, окрашенные крас

ками а, Ь, с (рис. 5.56); кодируем эти краски соответственно как

О, 1 , 2. В результате полученный граф Кёнига определяет внеш

нюю функцию F(y?i, 14, ¥>2) искомой декомпозиции:

/ (* 1 , *2 , *3 , * 4) = F{<Plixl> * 2), *4 , Хз, 14) ) .

Здесь функция трехзначной логики от четырех переменных пред

ставлена в виде оптимальной повторной декомпозиции одной функ

ции <pi от двух переменных и двух функций <р2 и F от трех пере

менных. Вид функции <pi был представлен выше.

Функция ч>г(х\, a?2i ^з) имеет вид (см. рис. 5.52)

а = {4, 6', 8'} Ь = {O', 2, 3, 6я, 8"> с = {0", 1, 5, 7. 8я}

Рис, 5.56

§5.9. Синтез функциональной декомпозиции

473

Таким образом, стратегия синтеза оптимальной функциональ

ной декомпозиции в fc-значной логике заключается в выполнении

следующих этапов:

— разбиение исходного пространства Р (Х ) на два сопряжен

ных, Р{Х а) и Р{ХЬ)\ Р{Х а) х Р{ХЬ) = Р{Х), Х аП Х ь = 0 ,

Хаи Х ь = Х ;

— построение графа противоречивости Gnp(Xa), его раскраска

и, если это необходимо для выполнения соотношения (5.8), осуще

ствление редукции его хроматического числа путем расширения

подпространства Р(Хь) до Р{Х'Ь), Х'ь = XbU &Ха\

— склеивание соцветных вершин графа Gnp(X a), кодирова

ние красок и построение соответствующих внутренних функций в

подпространстве Р (Х а)\

— построение графа противоречивости Gnp(X^), его раскраска

и, если это необходимо для выполнения соотношения (5.9), осу

ществление редукции его хроматического числа на основе расши

рения подпространства Р(Ф) до Р(Ф'), Ф' = ФЛХ(>;

— склеивание соцветных вершин графа Gnp(-Xb), кодирование

красок и построение соответствующих внутренних функций в под

пространстве Р{Х'Ь)]

— при необходимости дальнейшая декомпозиция полученных

внутренних функций на основе этой стратегии и в результате по

строение внешней функции F искомой декомпозиции.

§ 5.9. Синтез функциональной

декомпозиции заданной размерности

Многие практические задачи сводятся к синтезу функциональ

ной декомпозиции булевой функции, в которой полученные вну

тренние и внешняя функции имеют заданную размерность.

Рассмотрим синтез функциональной декомпозиции булевой

функции /(xj, Х2, ..., in) через функции от четырех переменных.

Тогда в выражении (5.5) параметры fc и s удовлетворяют неравен

ству к + з < 4. При этом возможны два случая: fc = s = 2 и

k(s) = 3, s(k) = 1.

В первом случае запрещенными фигурами построения деком

позиции булевой функции вида

Д Х ) = FfaiXa), М Ха), т(Хь), т(Хь))

являются квазиполные графы квазиплотности 5 Q(pi, fc,-) С

С Gnp(-Xa), Gnp(-X'b) (Pi — плотность, fc, — порядок квазиплотного

графа Q):

0 ( 5,0), Q (4,l), Q(3,2), 0(2,3).

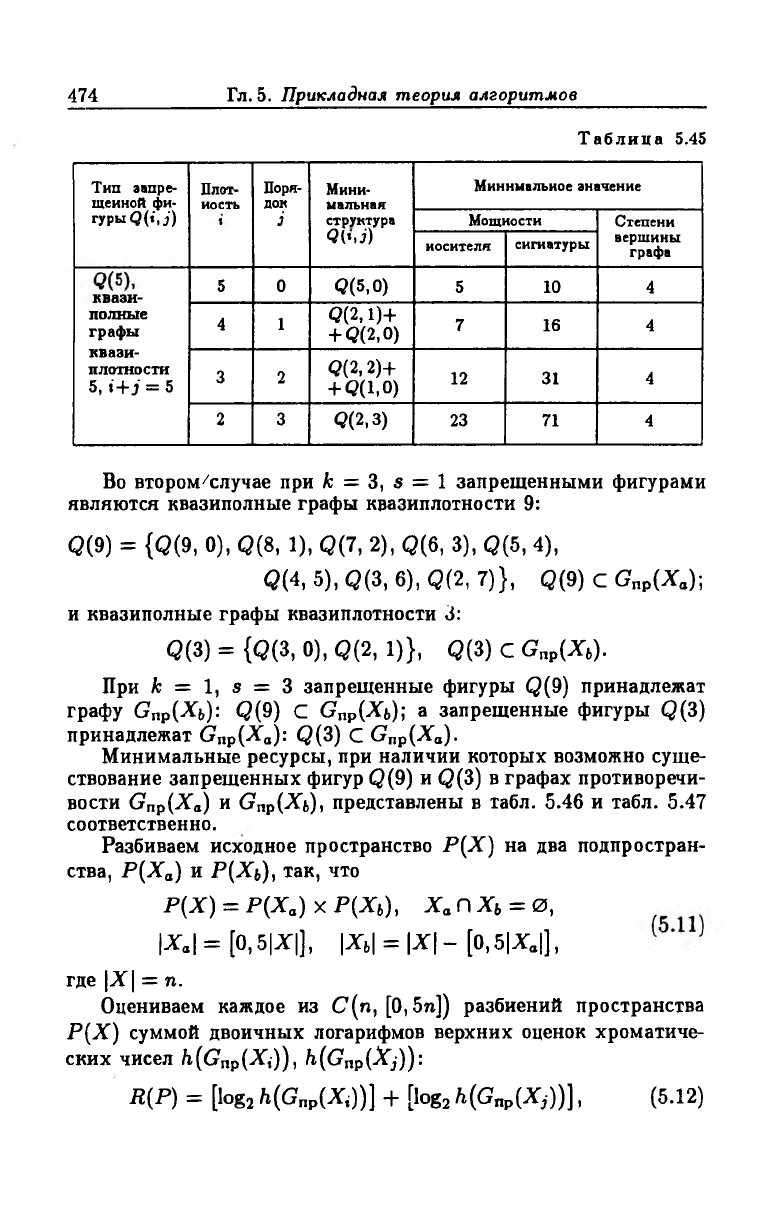
Минимальные ресурсы — вершинный, реберный, локально

топологический (степени вершин графа), — определяющие запре

щенные фигуры 0(5)i приведены в табл. 5.45.

474

Гл. 5. Прикладная теория алгоритмов

Таблица 5.45

Тип запре

щенной фи-

гуры Q (i,i)

Плот

ность

Поря

док

Мини

мальная

структура

Q (»,j)

Минимальное значение

Мощности

Степени

вершины

графа

носителя

сигнатуры

квази

полные

графы

квази

плотности

5, i+j = 5

5 0

Q( 5,0)

5 10

Q( 2 ,1 )+

+ Q(2,0)

7 16

3 2

Q (2 ,2 )+

+ 0 (1, o)

12 31 4

2 3

Q( 2,3)

23 71 4

Во втором/случае при к = 3, s = 1 запрещенными фигурами

являются квазиполные графы квазиплотности 9:

0 (9) = {Q(9, 0), Q(8, 1), 0(7, 2), 0(6, 3), 0(5, 4),

0(4, 5), 0(3, 6), 0(2, 7)}, 0(9) С Gnp(Xa);

и квазиполные графы квазиплотности 3:

0(3) = {0(3,0), 0 (2 ,1 )}, 0(3) С Gnp(Xb).

При к = 1, s = 3 запрещенные фигуры 0(9) принадлежат

графу Gnp(Xb): 0(9) С Gnp(Xb); а запрещенные фигуры 0(3)

принадлежат Gnp(-^a)-' 0(3) С Gnp(Xa).

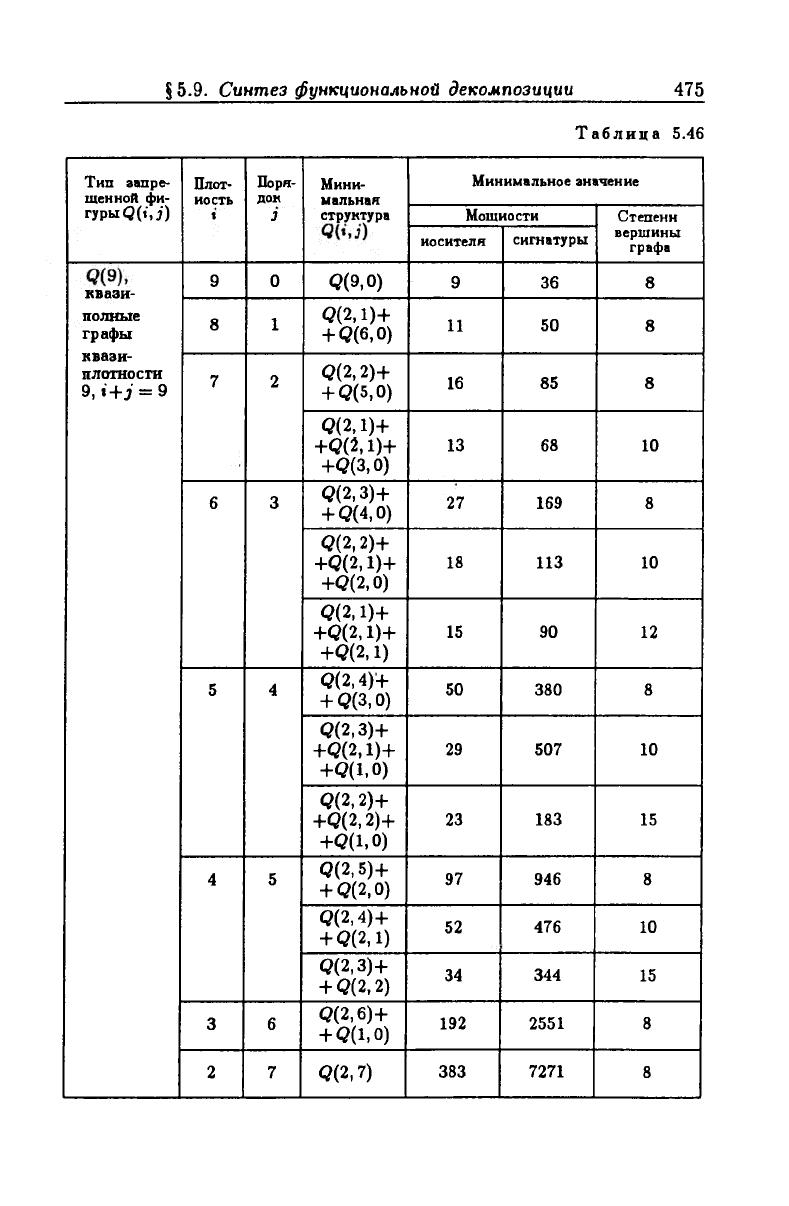
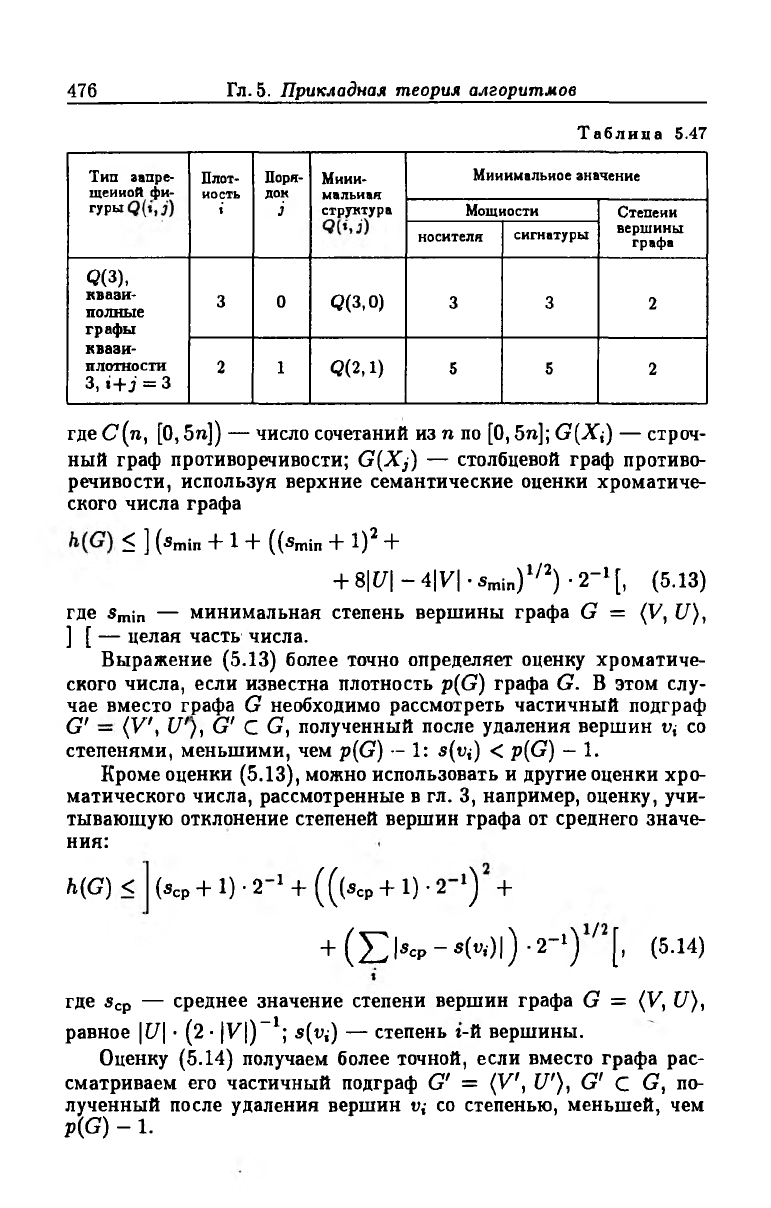
Минимальные ресурсы, при наличии которых возможно суще

ствование запрещенных фигур 0(9) и 0(3) в графах противоречи

вости Gnp(Xa) и Gnp(Xb), представлены в табл. 5.46 и табл. 5.47

соответственно.

Разбиваем исходное пространство Р (Х ) на два подпростран

ства, Р{Ха) и Р(Хь), так, что

F (X ) = P (I . ) x P № ) , Х аПХь = 0 ,

|Хо|=[0,5|Х|], \ХЬ\ = \Х \-[0,5|Хо|],

где |Х| = п.

Оцениваем каждое из С(п, [0,5п]) разбиений пространства

Р{Х ) суммой двоичных логарифмов верхних оценок хроматиче

ских чисел h(Gnp(Xi)), h(Gnp(Xj)):

R(P) = [log2 h{Gnp(Xi))] + [log2 Л(СПр( ^ ) ) ] , (5.12)

§5.9. Синтез функциональной декомпозиции

475

Таблица 5.46

Тип запре

щенной фи

гуры Q(i, j)

Плот

ность

Поря

док

Мини

мальная

Минимальное значение

структура

Мощности

Степени

носителя

сигнатуры

вершины

графа

квази

9 0 <?(9,0)

9 36 8

полные

графы

8 1

<?(2,1)+

+ <?(6,0)

кваэи-

плотностн

9, i + i = 9

7 2

<?( 2 ,2)+

+ <?(5,0)

16 85 8

«?(2 ,1)+

+ «?(2 ,1 )+

+<?(3,0)

6 3

(?(2,3)+

+ <?(4,0)

27 169 8

<?(2,2)+

+ Q (2 ,1)+

+Q (2 ,0 )

113 10

Q ( 2,1)+

+<?( 2 ,1)+

+<?(2,1)

15 90

5 4

Q (2,4)4-

+ Q (3,0)

50 380 8

Q (2 ,3 )+

+ Q (2 ,1 )+

+Q(i,o)

29 507 10

Q( 2,2 )+

+ Q (2 ,2 )+

+Q (1 ,0 )

23 183 15

Q (2 ,5 )+

+ Q(2,0)

946

Q (2 ,4 )+

+ <?( 2,1)

476 10

3 (2 ,3 )+

+ Q(2,2)

344

3 6

Q (2 ,6 )+

+ Q (1,0)

192 2551 8

2 7

Q (2,7) 383

7271

476

Гл. 5. Прикладная теория алгоритмов

Таблица 5.47

Тип запре

щенной фи

гуры

Плот

ность

Поря

док

Мини

мальная

структура

Минимальное значение

Мощности

Степени

вершины

графа

носителя

сигнатуры

<?(3),

квази

полные

графы

квази

плотности

3, i+ j = 3

3 0 <?(3,0)

3 3

2 1

<?(2,1)

5 5

где С(п, [0,5га]) — число сочетаний из га по [0,5га]; G(X{) — строч

ный граф противоречивости; G(Xj) — столбцевой граф противо

речивости, используя верхние семантические оценки хроматиче

ского числа графа

^ ] (smin + 1 + ((Smin + l ) 2 +

+ 8|С/| — 4|V| • smin) 1/2) • 2-1 [, (5.13)

где smin — минимальная степень вершины графа G = (V, U),

] [ — целая часть числа.

Выражение (5.13) более точно определяет оценку хроматиче

ского числа, если известна плотность p(G) графа G. В этом слу

чае вместо графа G необходимо рассмотреть частичный подграф

G' — (V7, U'), G' С G, полученный после удаления вершин V{ со

степенями, меньшими, чем p(G) — 1: s(uj) < p(G) — 1.

Кроме оценки (5.13), можно использовать и другие оценки хро

матического числа, рассмотренные в гл. 3, например, оценку, учи

тывающую отклонение степеней вершин графа от среднего значе

ния:

h(G) <

(■sCp + 1) • 2 1 + ^ ( s cp + 1) • 2 ^ +

+ (S k p -^ M l) '2_1) ' [> (5Л4)

где scp — среднее значение степени вершин графа G = (V, U),

равное \U\ • (2 ■ |V|)-1; s(v;) — степень г-й вершины.

Оценку (5.14) получаем более точной, если вместо графа рас

сматриваем его частичный подграф G' = (V7, U'), G' С G, по

лученный после удаления вершин и,- со степенью, меньшей, чем

p(G) - 1.

§5.9. Синтез функциональной декомпозиции 477

Разбиение вида (5.11) определяется использованием субмик-

ронной технологии, так как в этом случае дебаланс активизируе

мых цепей в нейронной сети будет оптимальным. Исследование

такого разбиения показало, что оценки (5.12), с помощью которых

выбирается оптимальное разбиение, близки друг к другу.

Действительно, порождение различных разбиений переменных

булевой функции /(*i, х2, ..., гп) эквивалентно применению пре

образований Джевонса к этой функции. Все соответствующие гра

фы Кёнига определяют функции, принадлежащие одному и тому

же типу (в смысле Джевонса), но все однотипные булевы функции

имеют одни и те же теоретико-структурные свойства, которые в ко

нечном счете объективно определяют декомпозиционные свойства

функции.

Рассмотрим синтез функциональной декомпозиции, реализую

щей булеву функцию f(x lt х2, .. .,х6), описывающую функциони

рование одного из узлов машины логического вывода, при задан

ных ограничениях k + s < 4:

на 3, 4, 7, 9, 16, 18, 22, 24, 25, 26,

. 34, 36, 37, 48, 50, 53, 58, 59, 62, 63,

/(*1, х2, ..., z6) - < о на 0) 2) 12) 13) 19) 23) 28) 31) 40)

43,44,45,46,49,55.

В результате оценки разбиений согласно (5-12) было выбрано раз

биение вида

Р(хг, х2, ..., х6) = P{xi, х2, х3) х Р(х4, х5, х6);

соответствующая таблица Вейча представлена в виде табл. 5.48 и

граф Кёнига — на рис. 5.57.

Таблица 5.48

х\х2%г

0 1

4 5

6 7

0 0 0 1

1 1

0 0

2 1

1 0 1 0

3 1 1

1 0 0

4 1

1 1

5 0

0 0 0

0 1

7 1 1

Строчный граф противоречивости Gnp(A'a) представлен на

рис. 5.58, а; он содержит запрещенную фигуру Q(5, 0) — пол

ный подграф плотности 5 (рис. 5.58,6). Для определения мини

мального сужения сигнатуры графа противоречивости и его оп-

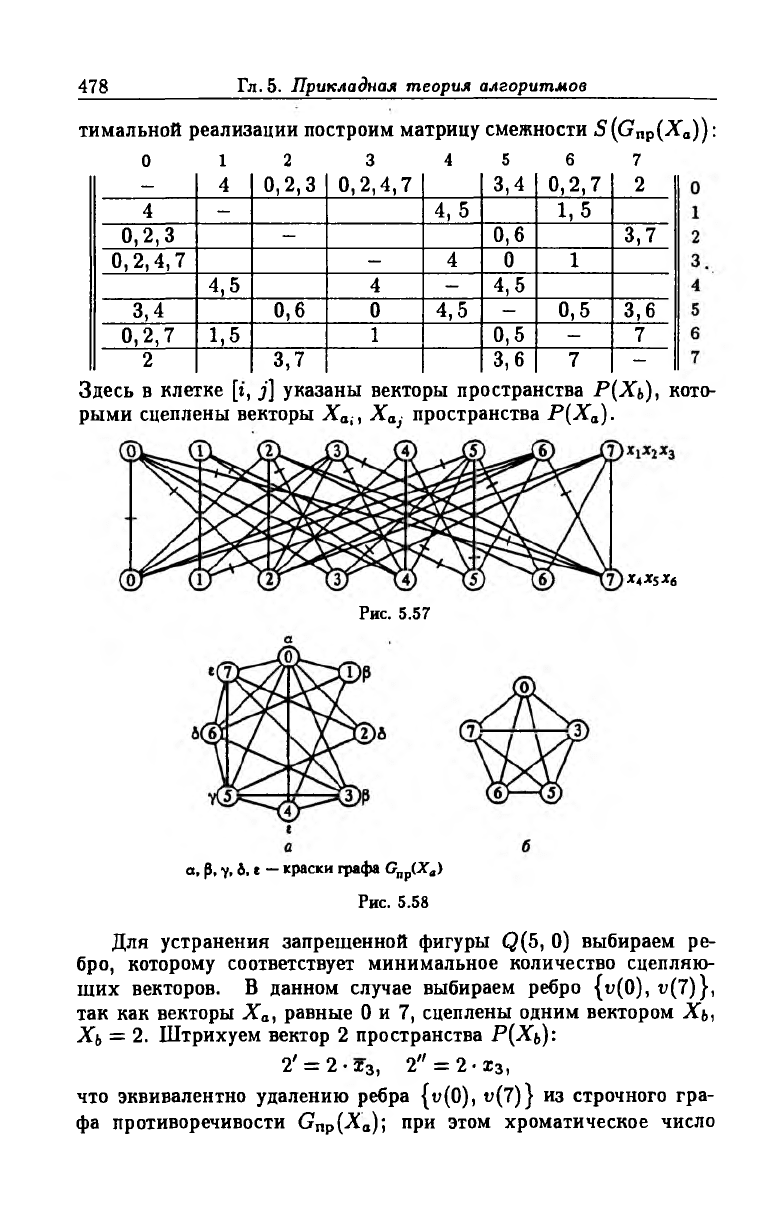
478

Гл. 5. Прикладная теория алгоритмов

тимальной реализации построим матрицу смежности S(Gnp(Xa)):

О 1 2 3 4 5 6 7

—

4 0,2,3 0,2,4,7

3,4 0,2,7 2

4,5

1,5

0,2,3

0,6

3,7

0,2,4, 7

- 4

0 1

4,5 4

4,5

3,4 0,6 0

4,5

0,5

3,6

0,2,7 1,5

1 0,5

2 3,7 3,6 7

Здесь в клетке [г, j] указаны векторы пространства Р(Хъ), кото

рыми сцеплены векторы X ai, X aj пространства Р(Х а).

Х4Х5Х6

Рис. 5.57

а, р, у. 6. « — краски графа Gnp(Xa)

Рис. 5.58

Для устранения запрещенной фигуры Q(5, 0) выбираем ре

бро, которому соответствует минимальное количество сцепляю

щих векторов. В данном случае выбираем ребро {и(0), v(7)},

так как векторы Х а, равные 0 и 7, сцеплены одним вектором Хь,

Хь = 2. Штрихуем вектор 2 пространства Р(Хь):

2' = 2 -х3, 2" = 2 -1 3,

что эквивалентно удалению ребра {и(0), и (7)} из строчного гра

фа противоречивости Gnp(-Xa); при этом хроматическое число

§5.9. Синтез функциональной декомпозиции

479

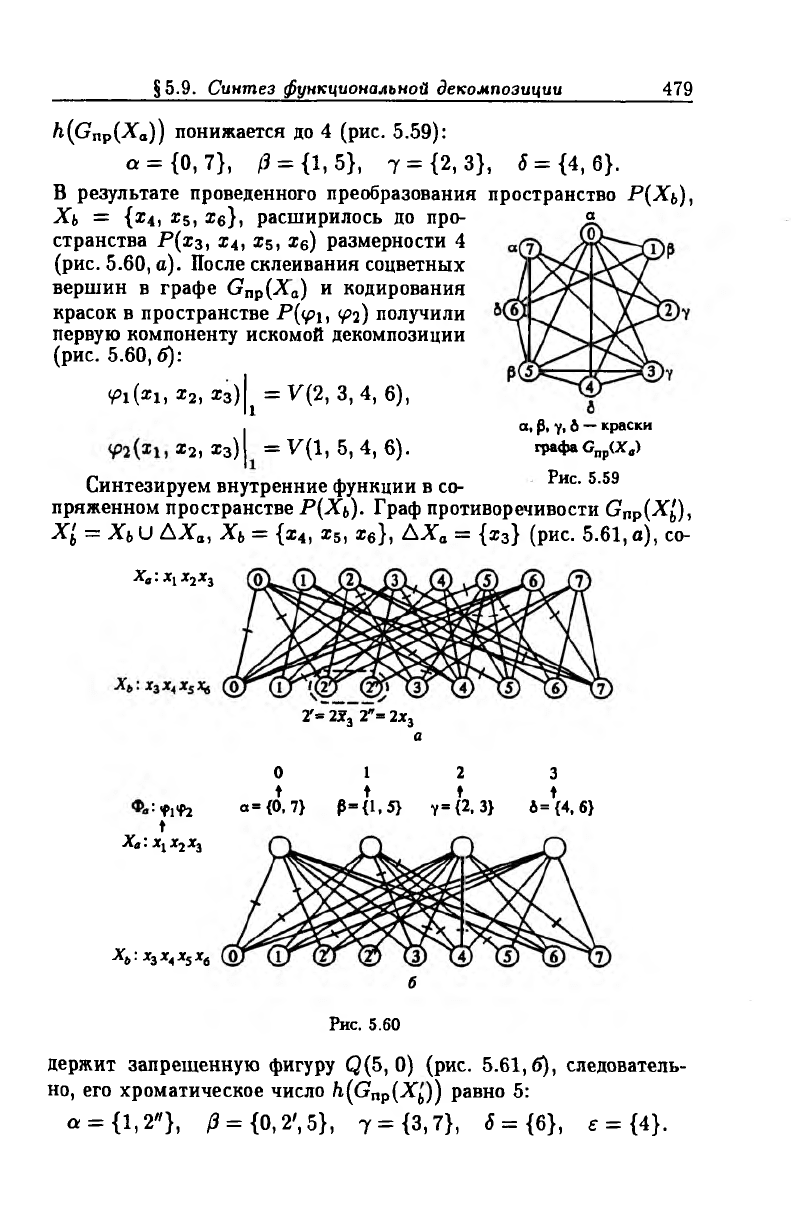
h{Gnp(Xa)) понижается до 4 (рис. 5.59):

а = {0,7}, /3 = {1,5}, 7 = {2,3}, 6 = {4, 6}.

В результате проведенного преобразования пространство Р(Хь),

Хь = {®4, х5, ®б}, расширилось до про

странства Р(хз, г4, г5, г6) размерности 4

(рис. 5.60, а). После склеивания соцветных

вершин в графе G ^ X a ) и кодирования

красок в пространстве P(<pi, <^2) получили

первую компоненту искомой декомпозиции

(рис. 5.60, 6):

<Ы*1, ®2, гз)^ = ^(2, 3,4, 6),

12, *з)| = У(1, 5, 4, 6).

Синтезируем внутренние функции в со

пряженном пространстве Р{Хь). Граф противоречивости G„p(^ ),

Х'ь = Хь U Д Х а, Хь = { 14, is, Яб}, Д Х а = {г 3} (рис. 5.61, а), со-

Ха: ^*2 *3

2'= 2У3 2"= 2х3

0 1 2 3

t t t t

: fif2 a= {0, 7} P= {1. 5} y={2,3} 6= {4, 6}

Xa: jtj jt2 x3

X„:x3xAxsx6

Рис. 5.60

держит запрещенную фигуру Q(5, 0) (рис. 5.61,6), следователь

но, его хроматическое число /i(Gnp(X j)) равно 5:

а = {1,2"}, /3 = {0,2',5}, Т = {3,7}, S = { 6}, е = {4}.

а. р, Vi 6 — краски

графа Gnp(Xa)

Рис. 5.59

480

Гл. 5. Прикладная теория алгоритмов

у Для редукции хроматического числа достаточно удаления од

ного из ребер графа Q(5, 0).

Для нахождения оптимального сужения сигнатуры графа про

тиворечивости Gnp(Xf)) строим матрицу смежности S(Gnp(Х'ь)) с

в, р, 1 ,6, е - краски графа

противоречивости Gnp(Xb)

Рис. 5.61

указанием сцепляющих векторов пространства Р(Фа), Фа = {ipx,

<Р2} (табл. 5.49). Удаляем ребро (и(1), и(6)}, взвешенное сцепляю-

Таблица 5.49

0 1

3 4 5 6 7

0 -

1,3 0

0, 2

0, 2,3

1,3 - 3

1,2

1, 2,3

1,3

0, 2 0, 2 0

0, 2,3

2" 0 0

0, 2

1,2

0, 2

—

0, 2

1, 2, 3

0, 2 2

5 1,3 -

2 2

0, 2,3 2

0, 2, 3 2 3 3

щим вектором 1, (1 <-»■ 11 X2*3) (рис. 5.62, а). В результате чи

сло красок графа противоречивости Gnp( ^ ) уменьшается до 4

(рис. 5.62, б):

а = {1,2", 6}, /? = {0,2'}, 7 = {3 ,7 }, 8 = {4,5}.

Склеиваем соцветные вершины и кодируем краски а, /?, j, S

соответственно векторами 0, 1, 2, 3 пространства Р(у>з, щ). По

лучаем, что внешняя функция определяется пятью переменными,

<fi, <f2, ¥>з, ¥>4, *4 (рис. 5.63):

/(хь х2, ...,х6) = F(ipi(xi, х2, х3), (р2{хъ * 2, *з),

¥>3(*3, * 4 , * 5 , * б ), ^ 4 (*3 , * 4 , * 5 , * б ) , 2Г4) ,