Горбатов В.А. Фундаментальные Основы Дискретной Математики. Информационная Математика

Подождите немного. Документ загружается.

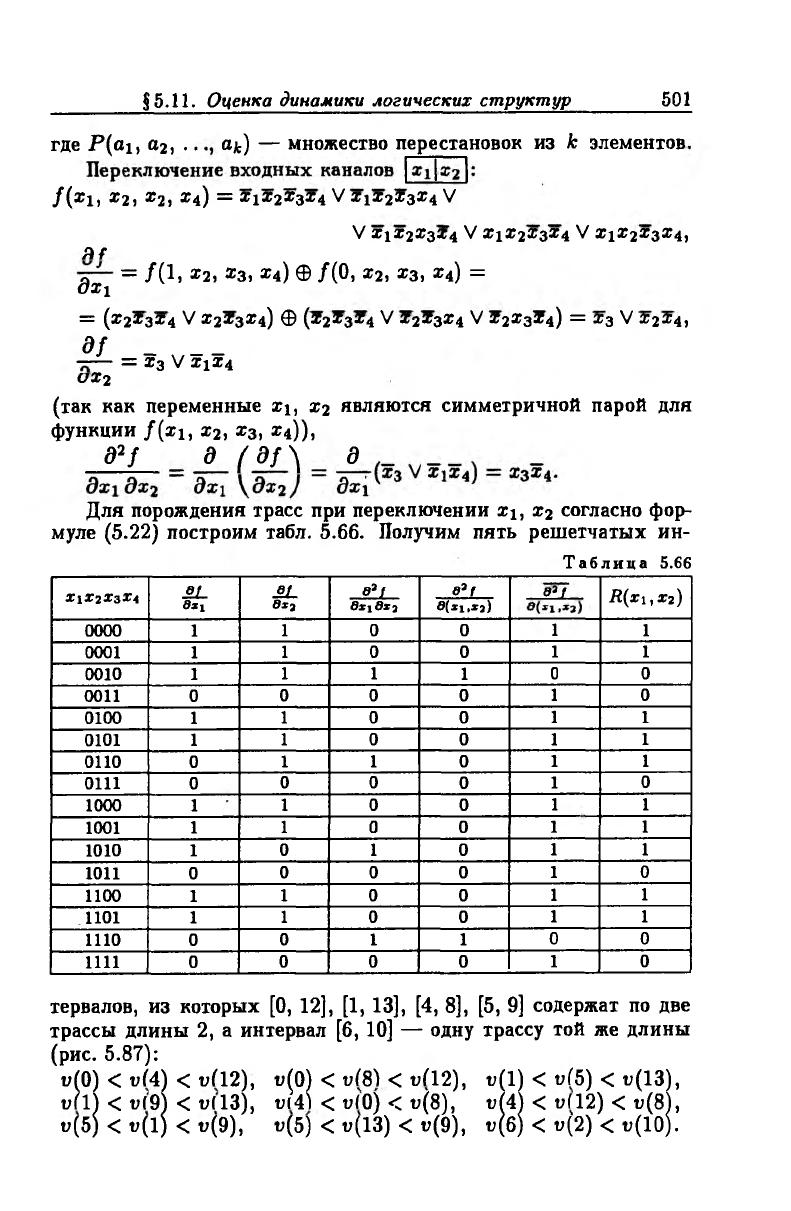
§5.11. Оценка динамики логических структур 501

где Р{аи а2, . . а*) — множество перестановок из к элементов

/ (хи Х2, х2, Х4) = Х\Х2 Х3Х4 V 1 1 1 2 1 3 * 4 V

V 1 1 1 2 X3*4 V Х1 Х2Х3Х4 V Х1Х2Х3Х4,

a t

= /(1, Х2, Хз. *4) Ф /(О, х2, Хз, х4) =

dxi

= (x2x3i 4 V Х2Х3Х4) ф (12X3X4 V х2х3х4 V Х2Х3Х4) = х3 V х2х4,

df _ __

— = i 3 V Х1Х4

ОХ 2

(так как переменные xi, Х2 являются симметричной парой для

функции /(х 1 , х2, х3, х4)),

а2/ д (df\ э

Для порождения трасс при переключении xi, Х2 согласно фор

муле (5.22) построим табл. 5.66. Получим пять решетчатых ин-

Таблица 5.66

271X2X3X4

8*1

ML.

8*2

e1/

8>/

R(x l,x2)

0*1 Of]

e(*i,*a)

0000 1

1 0 0

0001 1

1 0 0

1 1

0010 1

1 1

0011 0

0 0 0

1 0

0100 1

1 0 0

1 1

0101 1

1 0 0 1

0110 0

1 1 0

1 1

0111 0

0 0

1000 1

1 0 0

1 1

1001

1 0 0

1 1

1010 1

0 1 0

1 1

1011 0

0 0 0

1 0

1100 1

1 0 0

1101 1

1 0 0

1 1

1110 0

0 1 1

0 0

1111

0 0 0

1 0

тервалов, из которых [0, 12], [1, 13], [4, 8], [5, 9] содержат по две

трассы длины 2, а интервал [6, 10] — одну трассу той же длины

(рис. 5.87):

и(0) < uf4) < ufl2), и(0) < v(S) < v(12), u(l) < u(5) < u(13),

ufl) < u(9) < u(13), u(4) < u(0) < u(8), u(4) < u(12) < u(8),

u(5) < u (l) < u(9), u(5) < u(13) < t?(9), u(6) < u(2) < u(10).

502

Гл. 5. Прикладная теория алгоритмов

Рис. 5.87

Вычисление трасс для xi, хз и для других переключений двух

каналов оставляем для самостоятельной работы читателю, здесь

же приведем только результаты этих вычислений.

При переключении )а?х |а:з | имеется три трассы:

и(3) < v(l) < и(9), и(4) < и(12) < и(14), и(5) < t?(13) < и(15).

Множество трасс при переключении \x1\x4 :

и(3) < v{2) < и(10).

Множество трасс при переключении | а:2 |а?з I:

и(3) < и(1) < и(5), v(8) < и(12) < t?(14), и(9) < и(13) < и(15).

Множество трасс при переключении \x2\x4 :

и(3) < t?(2) < и(б).

Множество трасс при переключении j а?з|а:4 :

и(1) < и(3) < v(2).

Решетчатый интервал, содержащий хотя бы одну трассу, на

зывается критическим.

При переключении двух входных каналов нейрона получили 14

критических решетчатых интервалов:

Ji =[0,12], J2 =[1,13], J3 =[4,8], J4 =[5,9],

J5 =[6,10],' J 6 =[3,9], J 7 =[4,14], J8 = [5,15],

J9 =[3,10], Ло = [3, 5], Jn = [8,14], J\2 = [9,15],

Лз = [3,б], Ji4 = [l,2].

Вычислим трассы при переключении трех входных каналов ней

рона:

(*1. *2, *з), (*1, *2, *4), (*1, Х3, Х4), ( Х2 , Хз, Х4).

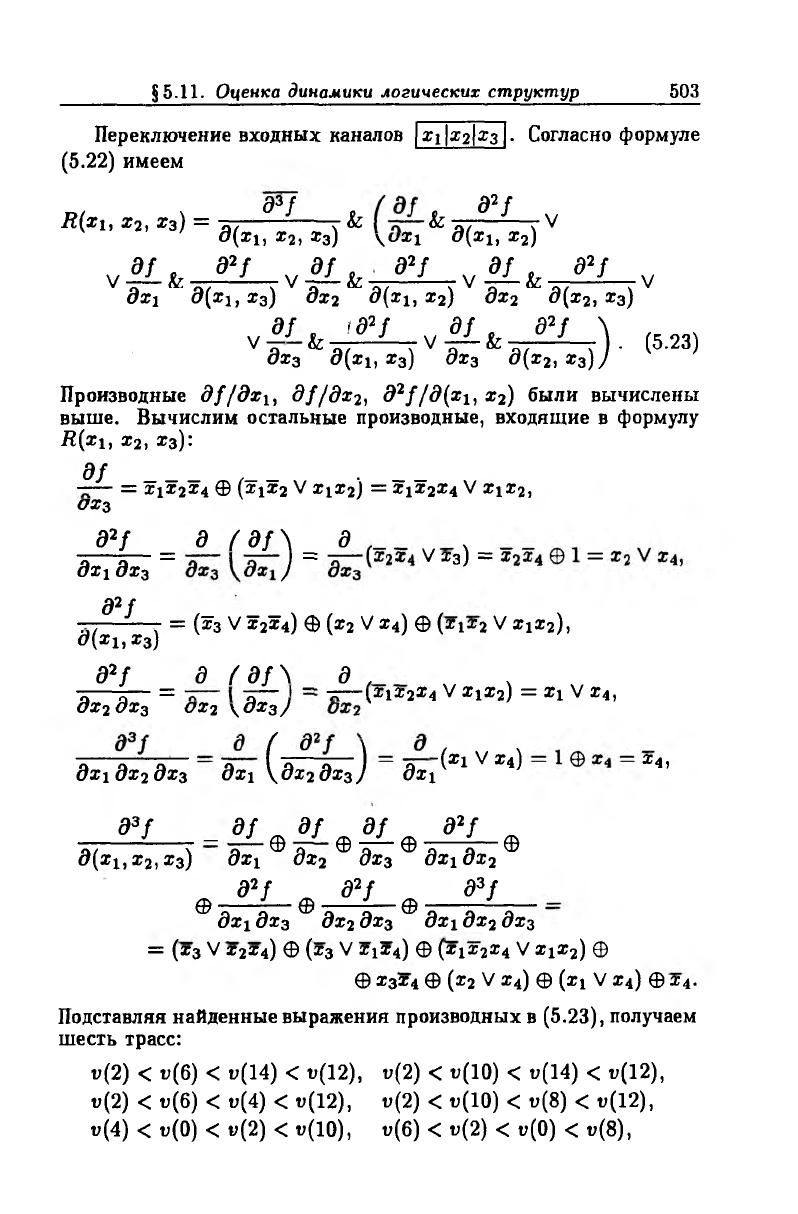
§5.11. Оценка динамики логических структур

503

Переключение входных каналов xi|x2|a;3 . Согласно формуле

(5.22) имеем

R (x u Х2, х 3) = <*1

------

, fc fc Jp - V

д (х ъ х 2, * 3) \ » * 1 о{х 1 , х2)

d f . d2f df „ d2f d f „ d2f

V —— Hr

--------

-----

V —— f c

---------

-----

V —— f c ----------

-----

dxi d(xi, x3) dx2 d{xi, x2) dx2 d(x2, x3)

v | / fe^ v f fc * Ц ) . (5.23)

dx3 0(zi, x3) ox3 d(x2, x3)J

Производные df/dxi, df/dx2, d2f/d(xi, x2) были вычислены

выше. Вычислим остальные производные, входящие в формулу

Д (* 1 , х 2, х 3):

d f

_____

___

- — = XiX2X4 ф (XiX2 V XiX2) = XiX2X4 V XiX2,

OX3

d2f d ( d f\ d 4

9 ^ д Г г = J = v I3) = =

d2f

______

—;

--------

= (x3 V I 2X4) Ф {X2 V X4) ф (XlX2 V XlX2),

d(x i,X3)

d2f d ( df\ d

я — ЪГ~ = я~~ ~ -Х— (Х1Х2Х4 V Z ix 2) = Xi V х 4 ,

ох2 0 x3 0 x2 \ дхз )

dxidx2 dx3 d x ii<dx2 dx3) dx^X l^ X4^ х*>

a3/ d f df d f d2f

- ® ф 77^- ф

----

5— ®

а(хх,Х2,хз) 0xx dx 2 #x3 dx\dx2

d2f d2f d3f

ф -— ^— ф -— ^— ф

0X !0x3 5x2 dx3 dx 1 0x2 dx3

= (x3 V X2X4) ф (x3 V X1X4) Ф (X !X 2X4 V X iX 2) Ф

ф X3X4 Ф (X2 V X4) ф ( x i V X4) Ф X4.

Подставляя найденные выражения производных в (5.23), получаем

шесть трасс:

v(2) < t>(6) < t»(14) < v(12), v{2) < u(10) < u(14) < v(12),

u(2) < u(6) < u(4) < u(12), v(2) < u(10) < u(8) < u(12),

u(4) < u(0) < u(2) < u(10), u(6) < v(2) < t?(0) < u(8),

504

Гл. 5. Прикладная теория алгоритмов

содержащихся в трех критических интервалах

Лб = [2, 12], Ji6 = [4, 10], Ji7 = [6, 8].

Поиск трасс при переключении переменных (®i, х2, 14), ( ii, х3,

хл), (х2, Хз, *4) оставляем читателю для самостоятельной работы.

Приведем результаты вычислений.

При переключении (*i, х2, *4) получаем семь трасс:

t?(0) < и(4) < и(5) < t?(13), и(0) < и(8) < и(9) < и(13),

и(1) < и(9) < и(8) < и(12), и(4) < и(0) < и(1) < и(9),

и(4) < и(12) < и(13) < и(9), v(5) < t?(l) < и(0) < t?(8),

и(5) < t»(13) < t»(12) < и(8),

содержащихся в четырех критических интервалах

Лв = [0,13], J 19 = [1, 12], J 20 = [4, 9], J 2i = [5, 8].

При переключении каналов (x i, 5С3, х4) получаем четыре трас

сы:

и(3) < и(1) < и(0) < и(8), и(3) < и(2) < и(0) < и(8),

и(4) < и(12) < и(13) < и(15), и(5) < и(13) < и(12) < и(14),

содержащиеся в трех критических интервалах

J 22 = [3, 8], J23 = [4, 15], /24 = [5, 14].

При переключении входных каналов (х2, хз, х4) получаем че

тыре трассы:

и(3) < и(1) < и(0) < и(4), и(3) < t?(2) < и(0) < v(4),

и(8) < ю(12) < и(13) < «(15), и(9) < и(13) < и(12) < t>(14),

содержащиеся в трех критических интервалах

^25 = [3, 4 ], J 26 = [8, 15], J27 = [9, 14].

Переключение входных каналов |Хх\х2\хз\х4\. Согласно (5.22)

имеем

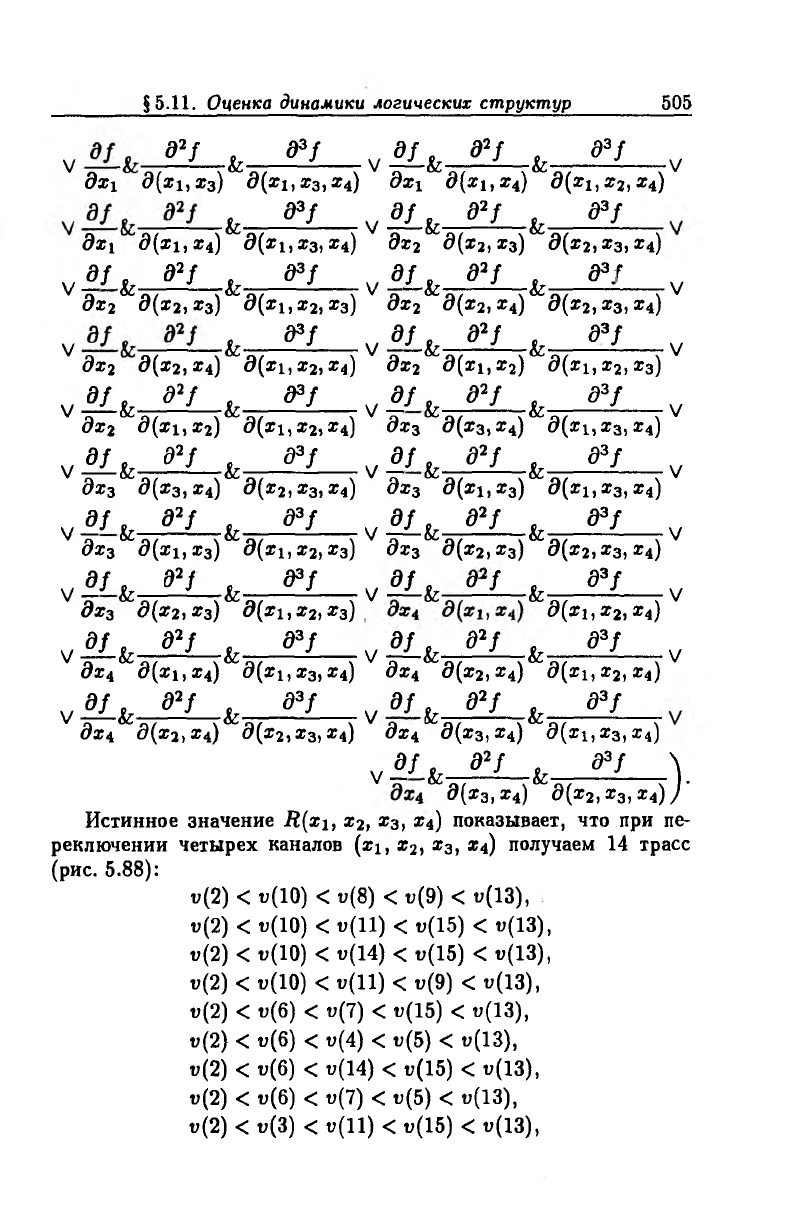
§5.11. Оценка динамики логических структур 505

v 2 !L _

dxi d(xi,x3)

03/

dx\ 0 (x i,x 4)

v j / fc_ g i L -

& i 9 ( i , , i 3)

0X2 0(*2>Х4)

v-glfc **/

0x2 д(* ь х2)

v i l f c - g l Л .

0x3 0(x3,x 4)

yj/fc g y

0X3 0(ll,X 3)

v i / fc_ ? y _

0x3 0 (^2, x3)

yjlfc g/

0 x4 0 (xb x4)

yjlfc. dU .

0X4 0(X2,X4)

0 (^ 1) Хз, X4

0(Xi,X3, X4

03/

0 ( x i,x 2, хз

03/

0 (xi, X2 , x4

03/

0(xi,x 2,x 4

03/

0(X2 ,X3 ,X4

03/

0(xi, X2) Хз

0 3/

0 (xi, X2 , x3

0 3/

0(Xi,X3 ,X4

0 3/

0(x2 ,X3, X4

v 1 L fc.

gy ■

0X1 0(x i,x 4)

53/

yjlfc gL.

9i 2 a ( i „ I3)

у °LkJ>lL .

0X2 0(X2, X4)

v«Ifc_»y_

« . j e l l , , . , )

y | / f c W fc

0X3 0(x3, X4 )

y|/fc^fc

0X3 0(Xl,X3)

yilfc_£y_

« 4 « ( » .,!,)

yilfc a..L ,fc

уЩ . а-У .

0X4 0(x2, x4)

у»/,: »У

0X4 0(x3, X4 )

y j / f c g / . fc

9 ( i3 ,n )

0(X1,X2,X4)

03/

0(X2,X3,X4)

£ jf

____

0(X2, X3, X4)

d3f

0(Xl,X2,X3)

0 3/

0(Xl,X3,X4)

^3/

0(Xi,X3,X4)

a 3/

0 (s2,x 3,x 4)

d3f

0(Xl,X2,X4)

03/

0(Xl,X2,X4)

03/

0(X1,X3, I 4)

0 3/

)•

0(*2i *3i *

)

Истинное значение i?(x

, x2)

x4) показывает, что при пе

реключении четырех каналов (xi, х2, х3, х4) получаем 14 трасс

(рис. 5.88):

«(2) < «(10) < «(8) < «(9) < «(13),

«(2) < «(10) < «(И) < «(15) < «(13),

«(2) < «(10) < «(14) < «(15) < «(13),

«(2) < «(10) < «(11) < «(9) < «(13),

«(2) < «(6) < «(7) < «(15) < «(13),

«(2) < «(6) < «(4) < «(5) < «(13),

«(2) < «(6) < «(14) < «(15) < «(13),

«(2) < и(б) < «(7) < «(5) < «(13),

«(2) < «(3) < «(11) < «(15) < «(13),

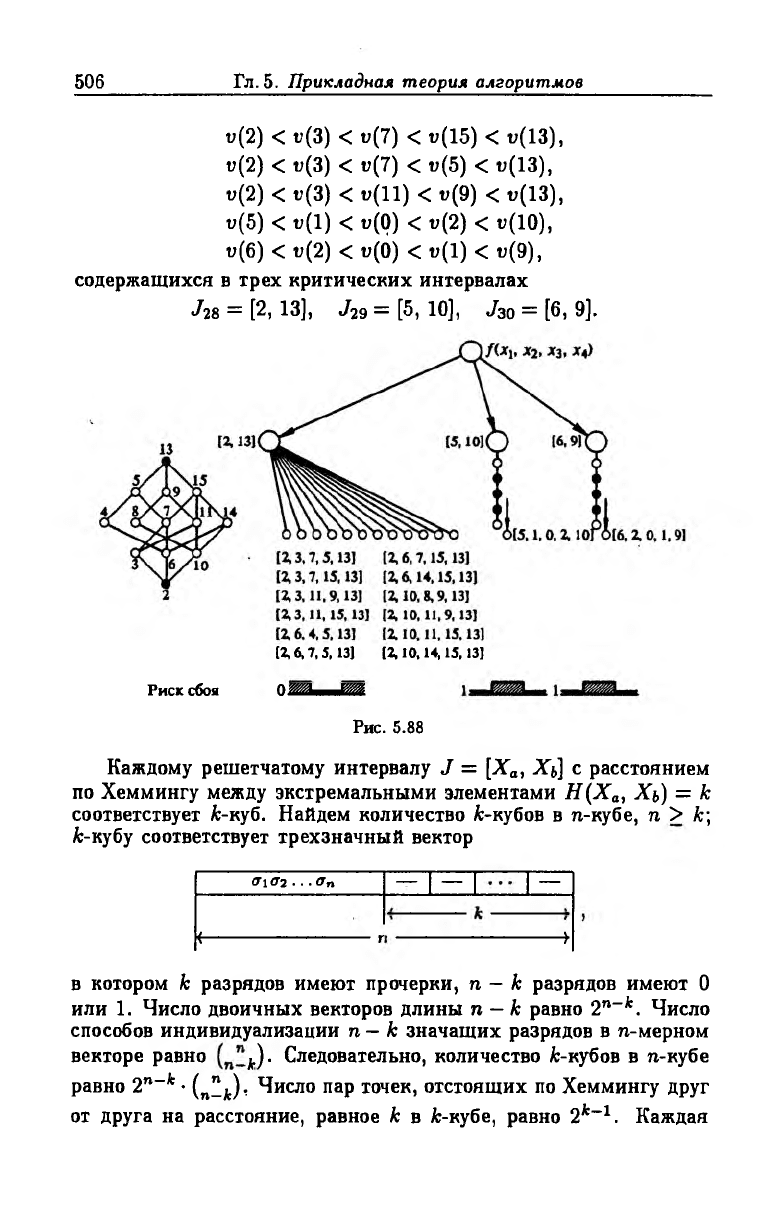
506

Гл. 5. Прикладная теория алгоритмов

v(2) < ю(3) < v(7) < v(15) < v(13),

v(2) < v(3) < v(7) < v(5) < u(13),

v(2) < t?(3) < v (ll) < u(9) < u(13),

u(5) < u (l) < u(Q) < v(2) < t?(10),

u(6) < v(2) < u(0) < u (l) < u(9),

содержащихся в трех критических интервалах

J28 = [2, 13], J-ig = [5, 10], J 30 = [6, 9].

[2,6,7,5,13] [2,10,14,15,13]

Риск сбоя О Ж - Ш

Рис. 5.88

Каждому решетчатому интервалу J = [Х0, Xj] с расстоянием

по Хеммингу между экстремальными элементами Н(Ха, Хь) = к

соответствует fc-куб. Найдем количество fc-кубов в n-кубе, п > fc;

fc-кубу соответствует трехзначный вектор

o\o% ...on

— — —

<-- - - - - - - - - - - - - ----------------------------- г

----------------

>■

в котором к разрядов имеют прочерки, п — fc разрядов имеют О

или 1. Число двоичных векторов длины п — к равно 2п~к. Число

способов индивидуализации п - fc значащих разрядов в п-мерном

векторе равно д.). Следовательно, количество fc-кубов в п-кубе

равно 2п~к • (n2jt)’ Число пар точек, отстоящих по Хеммингу друг

от друга на расстояние, равное к в fc-кубе, равно 2*-1 . Каждая

§5.11. Оценка динамики логических структур 507

пара точек соответствует возможному переключению к каналов;

при этом фактическое переключение возможно по одной из А:! це

пей.

Следовательно, число цепей длины к в одном А;-кубе равно

2*-1 ■ А:! Отсюда получаем, что возможное количество цепей Nu

длины к, каждая из которых может быть трассой, в n-кубе равно

"■« = 2”"‘ ■(„!*)■ 2‘"‘ ' W = 2”‘ ‘ • (п - ' Н

Для рассматриваемого нейрона:

из 96 цепей длины 2 образуют трассы 14 цепей;

из 192 цепей длины 3 — 13 цепей;

из 192 цепей длины 4 — трассы 3 цепи.

Если допустить что переключения каналов равновероятны, то:

с вероятностью 0,15 возможна ложная информация при пере

ключении двух каналов;

с вероятностью 0,07 — при переключении трех каналов;

с вероятностью 0,01 — при переключении четырех каналов.

Из 480 цепей трассами являются 30; наиболее “опасным” в

случае порождения ложной информации является переключение

(0010) <-> (1101).

Порождение трасс для выходных элементов составляет пер

вый этап синтеза “наихудшей” в смысле переходных процессов

сигнальной части — входной сигнальной программы при модели

ровании аномалий динамических свойств логической структуры.

Вторым этапом является отображение найденных в пространстве

P {zit z2, • ■ •) zk,x) критических решетчатых интервалов в прост

ранство Р(х 1, Х2, ..., *п), где Z{ (г = 1, 2, ..., квж) — входные

каналы выходного элемента; х\, х2, ..., хп — входные каналы ло

гической структуры.

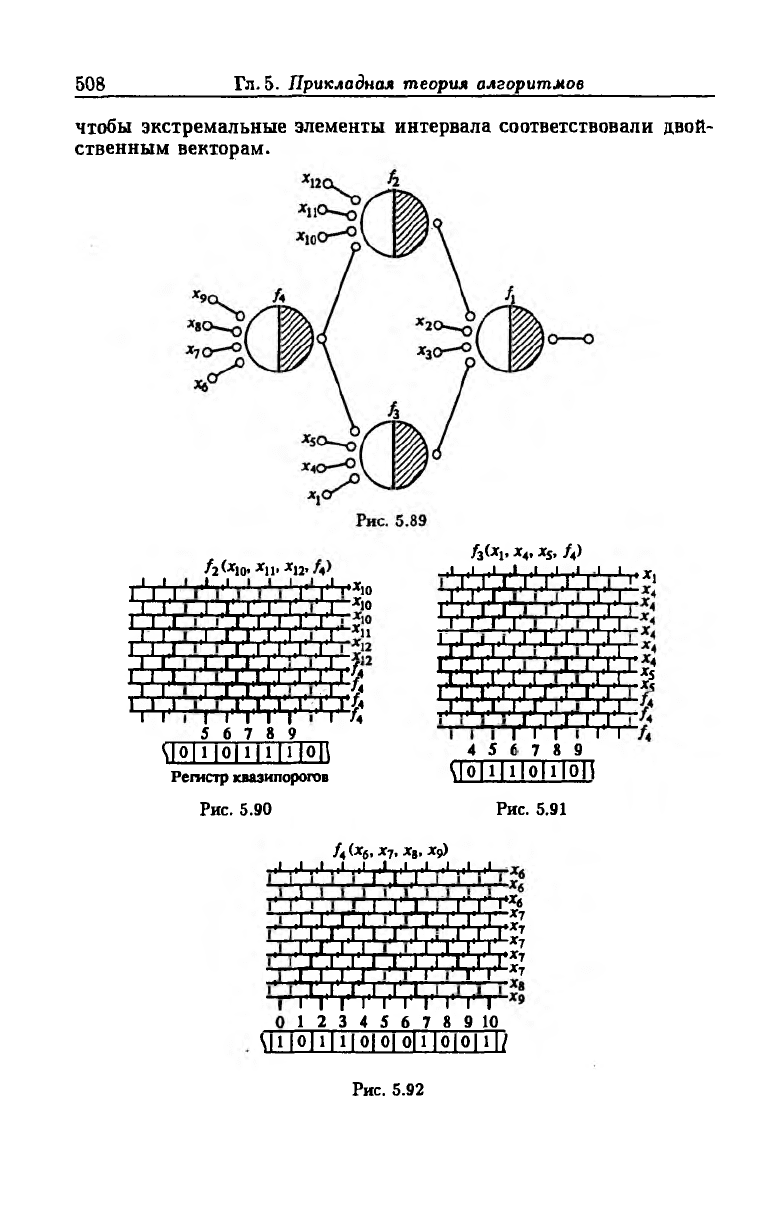
Рассмотрим логическую структуру в виде нейронной сети

(рис. 5.89), состоящей из нейронов гексагональной структуры,

реализующих булевы функции:

Л (/2, * 2, х3, /3)^= V(0, 1, 2, 12, 13) (ее реализация в виде

нейрона гексагональной структуры представлена на рис. 5.85, где

xi = /2> х4 = /3);

/2(^10, * и , *12, /4)|j= V(5, 7, 9, 10, 11, 13) (рис. 5.90);

/з(*1, * 4, хь, /4)^= V(3, 4, б, 11) (рис. 5.91);

f4(x6, х7, х8, *9)|х= V(0, 3, 7, 8, 15). (рис. 5.92);

Учитывая, что невыходные элементы нейронной сети имеют

свойство “фильтрации”, каждый критический интервал простран

ства Рк„ будем отображать в соответствующий критический ин

тервал пространства Рп (для рассматриваемого случая квх = 4,

п = 12) с максимальным расстоянием по Хеммингу в пределе так,

508

Гл. 5. Прикладная теория алгоритмов

чтобы экстремальные элементы интервала соответствовали двой

ственным векторам.

fi (*10. *11> *12’

,гт~г

JL.Q

& г

5 6 7 8 9

Slol Цо|

1 1 1

ji |о~П

Регистр квазипорогов

Рис. 5.90

Т**10

* 10

*■*11

/3(*1, х4, х5, /4)

,i ,1 ,,i „1 ,1 I .1

аЭ ?

W ?

У г У

т а 1

5SP

4 5

ШИ

гт

7 8 9

ш ш \

Рис. 5.91

Г *1

Г *

/4 (*6. * 7. *8. *9>

I .,1 „I ,,1 ,,1 A ,I .J J L ,,I .4-

Т О

т а

П г т

l . l j

EXT

, 111 |^г*б

r x ic c s ;

й Ж ; ;

,.1 .Ц.11.1 *7

1* Г I' I" I' Г I1 Г 1

2 3 4 5 6 7 8 9 10

\11 IО j 11 11 о| 0| о|1 10101 11/

Рис. 5.92

§5.11. Оценка динамики логических структур

509

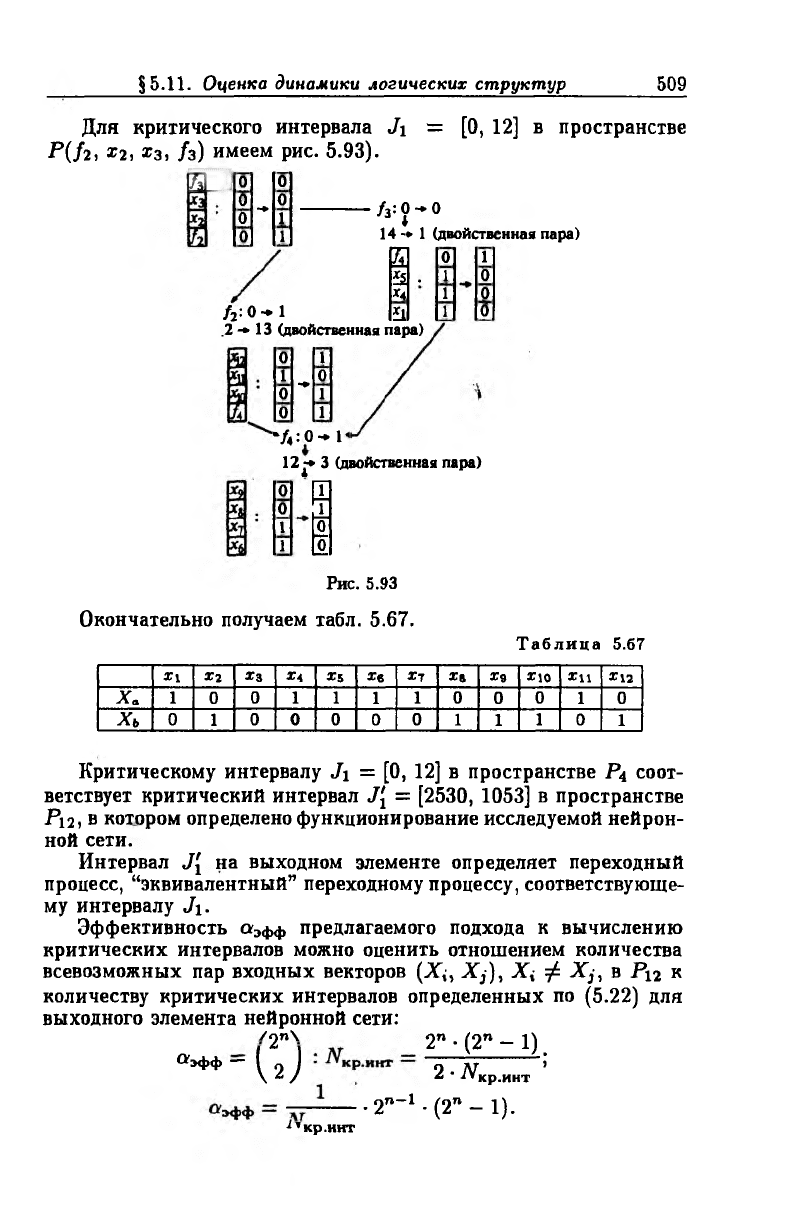
Для критического интервала J\ = [0, 12] в пространстве

-Р(/г. *2> *з> /з) имеем рис. 5.93).

1ЙВ

•ф

0 1

/3: 0 -* О

14 -* 1 (двойственная пара)

/2:0~1

.2 -» 13 (двойственная пара)

1 0

£1

0 1

•ф

0 1

-/«: 0-1-

12 j* 3 (двойственная пара)

Рис. 5.93

Окончательно получаем табл. 5.67.

Т а б ли ц а 5.67

хг

хъ

х*

*5 *6

Xs Xio

Хц

*12

Х а 1

0 1 1

1 0

Хь

0 0 0 0 0 1

Критическому интервалу Ji = [0, 12] в пространстве Р4 соот

ветствует критический интервал J[ = [2530, 1053] в пространстве

Р12, в котором определено функционирование исследуемой нейрон

ной сети.

Интервал J[ на выходном элементе определяет переходный

процесс, “эквивалентный” переходному процессу, соответствующе

му интервалу J\.

Эффективность а эфф предлагаемого подхода к вычислению

критических интервалов можно оценить отношением количества

всевозможных пар входных векторов (X,-, Xj), Х{ ф Xj, в Рц к

количеству критических интервалов определенных по (5.22) для

выходного элемента нейронной сети:

/2п\ 2" • (2П - 1)

“• * * ~ Ы 2 ■ JVkp.hht ;

------

2 - ‘ -(2"-1).

Л’ кр.ННТ

510

Гл. 5. Прикладная теория алгоритмов

Для рассматриваемого случая

-(D

®эфф :

30 =

8 386560

= 279 552.

Выполняя аналогично отображение остальных 13 критических

интервалов при переключении двух каналов выходного элемента,

получаем

|(1, 13)

./ 4( 5 ,

J?\

М 3, 9)

Js (5, 15)

•М З, 5)

/12(9, 15)

0306, 3229),

1381, 2205),

,(0866, 2205 ,

4(1378, 3741),

JL (0870, 3225),

J '2(0357, 3738),

/з(4, 8)

Л (6,10)

/т(4, 14

М 3, Ю)

/и (8, 14)

Л з(3, 6)

Л(3554, 0029),

4(4066, 0541),

4(3554, 1565),

4(0994, 2588),

4 i (0229, 3866),

4 з(0998, 3605),

j{ 4(0486, 2585).

/ 14( 1, 2)

Найдем отображение критических интервалов при переключе

нии трех каналов выходного элемента: Jis(2, 12), /ie(4, 10),

/ 17 (6 , 8), J i8(0, 13), /19(1 , 12), /20(4 , 9), J2i(5, 8), /22(3 , 8),

/ 2з (4 , 15), J24(5 , 14), J 25(3, 4), J 26(8, 15), /27(9 , 14).

Отображение Jis(2 ,12) ->4s(0738,3357) показано на рис. 5.94.

2 -. 13

1 2 -3

1 1 0 0 0 1 0

0 0 11

1 0 1

/3:0~0

х?

0 1

1 1

0 1

001011100010

llilolilolololilililoir

Рис. 5.94

Аналогично отображаем остальные 12 интервалов:

/ 1б (4 , Ю )

/18(0, 13)

/20 4, 9)

/22(з, 8)

/ 24( 5 , 14)

/26 (8, 15)

/(6(1250, 2845),

4 8(2402, 1181),

4 0(3426, 0157),

JL 0994, 2077),

/L(1506, 3613),

4б(2405, 1690),

/ 1 7 (6 , 8 )

/ie(l, 12)

/ 21( 5 , 8 )

/аз 4, 15)

/25(3 , 4)

/ 27( 9 , 14)

{7(1762, 2333),

19(0482, 3101),

JL 1506, 2077),

4з(3426, 1693),

4 5(0998, 3097),

4 7(0485, 3610).