Горбатов В.А. Фундаментальные Основы Дискретной Математики. Информационная Математика

Подождите немного. Документ загружается.

§5.11. Оценка динамики, логических структур

511

Определим отображение критических интервалов «/2в(2, 13),

^29(5, 10), Узо(6, 9) в пространство входных векторов нейронной

сети — в пространство Р12.

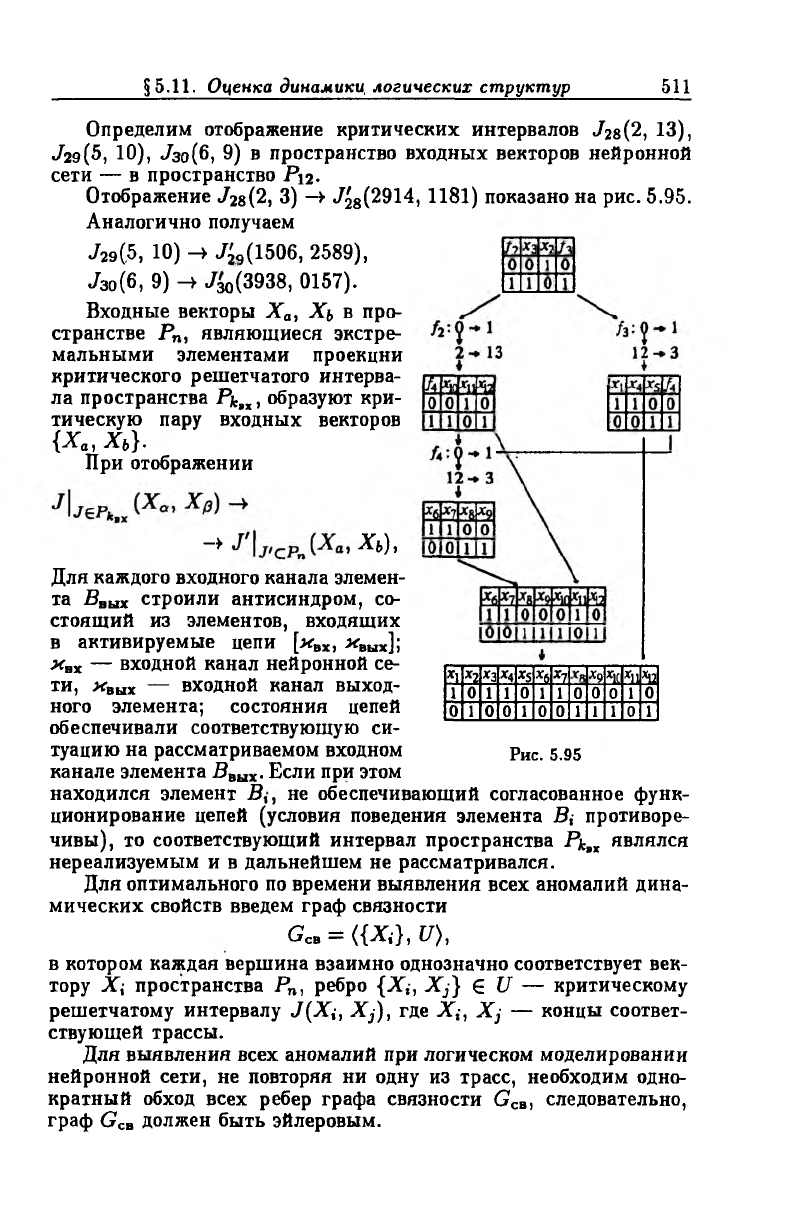
Отображение 7г8(2, 3) -> ^ 8(2914, 1181) показано на рис. 5.95.

Аналогично получаем

J29(5, 10) -► ^<,(1506, 2589),

J 30(6, 9) -► 7зо(3938, 0157).

Входные векторы Ха, Х ь в про

странстве Рп, являющиеся экстре

мальными элементами проекции

критического решетчатого интерва

ла пространства Р*,х, образуют кри

тическую пару входных векторов

{Ха, Хь}.

При отображении

-* *»)■

Для каждого входного канала элемен

та Ввых строили антисиндром, со

стоящий из элементов, входящих

в активируемые цепи [хвх, х вых];

хвж — входной канал нейронной се

ти, х вых — входной канал выход

ного элемента; состояния цепей

обеспечивали соответствующую си

туацию на рассматриваемом входном

канале элемента Ввыж. Если при этом

находился элемент В,, не обеспечивающий согласованное функ

ционирование цепей (условия поведения элемента Bi противоре

чивы), то соответствующий интервал пространства Р*,х являлся

нереализуемым и в дальнейшем не рассматривался.

Для оптимального по времени выявления всех аномалий дина

мических свойств введем граф связности

GCB = ({Xi}, U),

в котором каждая вершина взаимно однозначно соответствует век

тору X,- пространства Р„, ребро {X,, Xj} G U — критическому

решетчатому интервалу J(Xi, Xj), где Xi, Xj — концы соответ

ствующей трассы.

Для выявления всех аномалий при логическом моделировании

нейронной сети, не повторяя ни одну из трасс, необходим одно

кратный обход всех ребер графа связности GCB, следовательно,

граф GCB должен быть эйлеровым.

*1 хг

х4

*0 *7

хк *11*12

1 1 0 1 1

0 0 1

1 0

0 0

1 1 1 0 1

Рис. 5.95

512

Гл. 5. Прикладная теория алгоритмов

Для минимизации времени формирования входных векторов

X,- необходимо отсутствие их повторения, следовательно, граф G«,

должен быть гамильтоновым.

Используя характеризаиионный анализ, можно показать, что

граф связности GCB эйлеров и гамильтонов тогда и только тогда,

когда его цикломатическое число v(GCB) равно нулю и его степень

S(GCB) не превышает двух:

K G «)= 0)& (5(G cb)< 2).

При этих условиях граф GCB является линейно упорядочивае

мым. Запрещенными фигурами исследуемого свойства графа связ

ности являются циклы и вершины со степенью, превышающей 2.

Если граф GCB не является эйлеровым и гамильтоновым, то

расширением носителя {ДХ,} устраняем циклы и вершины X,

со степенью S(X ,) > 3 и линейно упорядочиваем граф GCB.

Линейно упорядоченный граф GCB = ({X,- U ДХ,}) U) опреде

ляет входную сигнальную программу выявления аномалий дина

мических свойств нейронных сетей.

Анализ графов связности для реальных сетей показал их ма

лую связность. Учитывая это свойство, предложим следующий

эффективный алгоритм расширения носителя графа GCB и его

линейного упорядочивания:

1) GCB :=G i;

2) 5(G ,) < 2 ? Если да, то переходим к п. 3), если нет — к

п. 4);

3) V (G,) > 0 ? Если да, переходим к п. 4), если нет ^кп.6);

4) определяем цепь максимальной длины 7rmax (в пределе —

остов, графа) G,-;

5) G, \ тгтах := G,-, в результирующем графе штрихуем повто

ряющиеся векторы X,-. Переход.к п. 2);

6) линейно упорядочиваем граф ({Х, иД Х ,}, U);

7) конец.

Пусть граф связности GCB = ({X,}, U) (рис. 5.96, о) имеет вид

{X,/ i = а, Ь, с, d, е, к, ш},

и = {{Х0, Х ь}, {Ха, Х с}, {Ха, Х Л , { х ь, Х с}, {ХЬ, Х е},

{Хь, Х т }, {Хс, Хе}, {Хс, Х Л , {Хс, Xjt}, {Хе, Xjfc},

{Хе, Хт }, {Xd, Х к], {Xd, Х т }, {Xjt, х т }}-

Имеем запрещенные фигуры графа связности

X, Ха

Хь х с

x rf х е x fc

x m

5(Х .) 3 4

4 4

§5.11. Оценка динамики логических структур 513

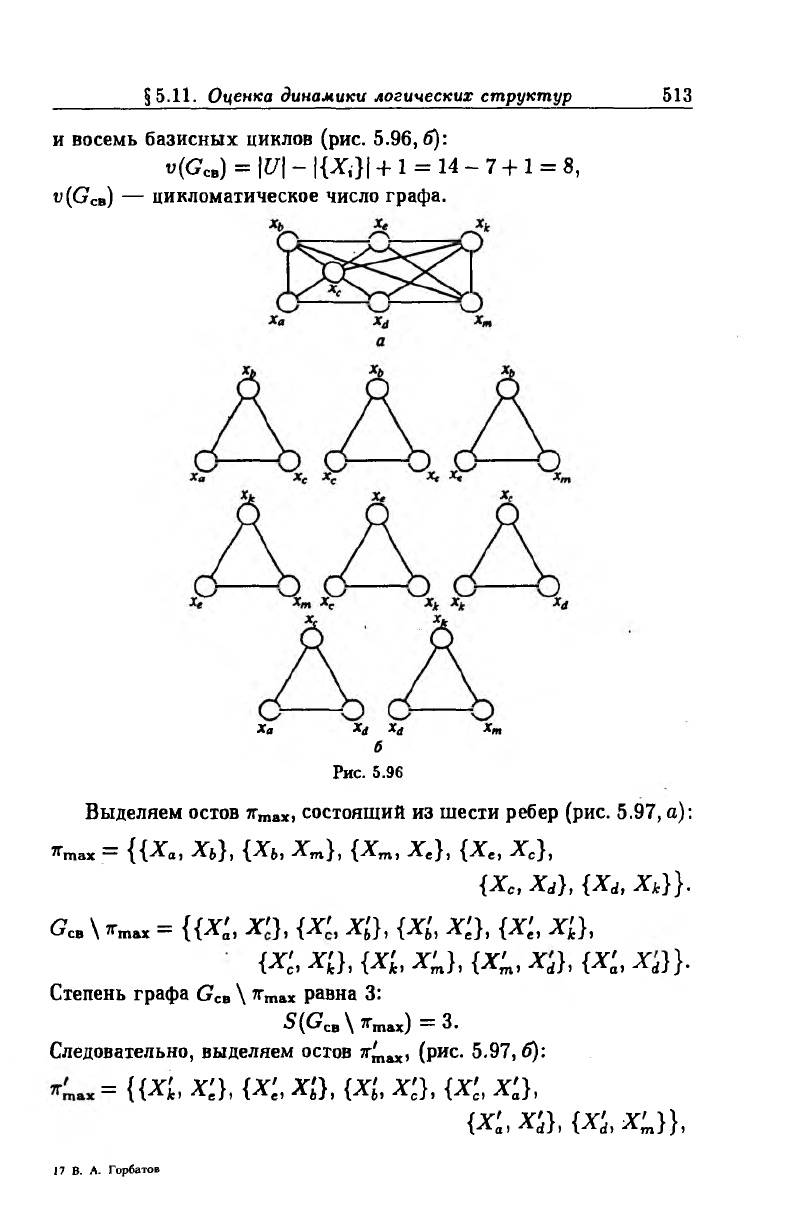
и восемь базисных циклов (рис. 5.96,6):

«(Сев) = |U\ - \{Xi}\ + 1 = 14 - 7 + 1 = 8,

v(GCB) — цикломатическое число графа.

Хд Хд Х4 хт

Рис. 5.96

Выделяем остов тгтах, состоящий из шести ребер (рис. 5.97, а):

^max =

{{Ха, Хь}, {Хь, х т }, {Хт , Хе}, {Хе, Хс},

{Хс, Xd), {Xd, Xk}}.

Gcb \ 7Tmax = {{X'a, X'}, {X', XD, {Xi, X'e], {Xi, X'k},

{X'c, X'k], {X'k, XI), {X.'m, Xd], {X'a, Xd}}.

Степень графа GCB \ ^max равна 3:

S(G CB \ ^max) = 3.

Следовательно, выделяем остов т г ^ , (рис. 5.97,6):

= { д а , К ), д а а д , д а а д , д а , а д ,

д а , а д , д а , а д } } ,

17 В. А. Г орбатов

514 Гл. 5. Прикладная теория алгоритмов

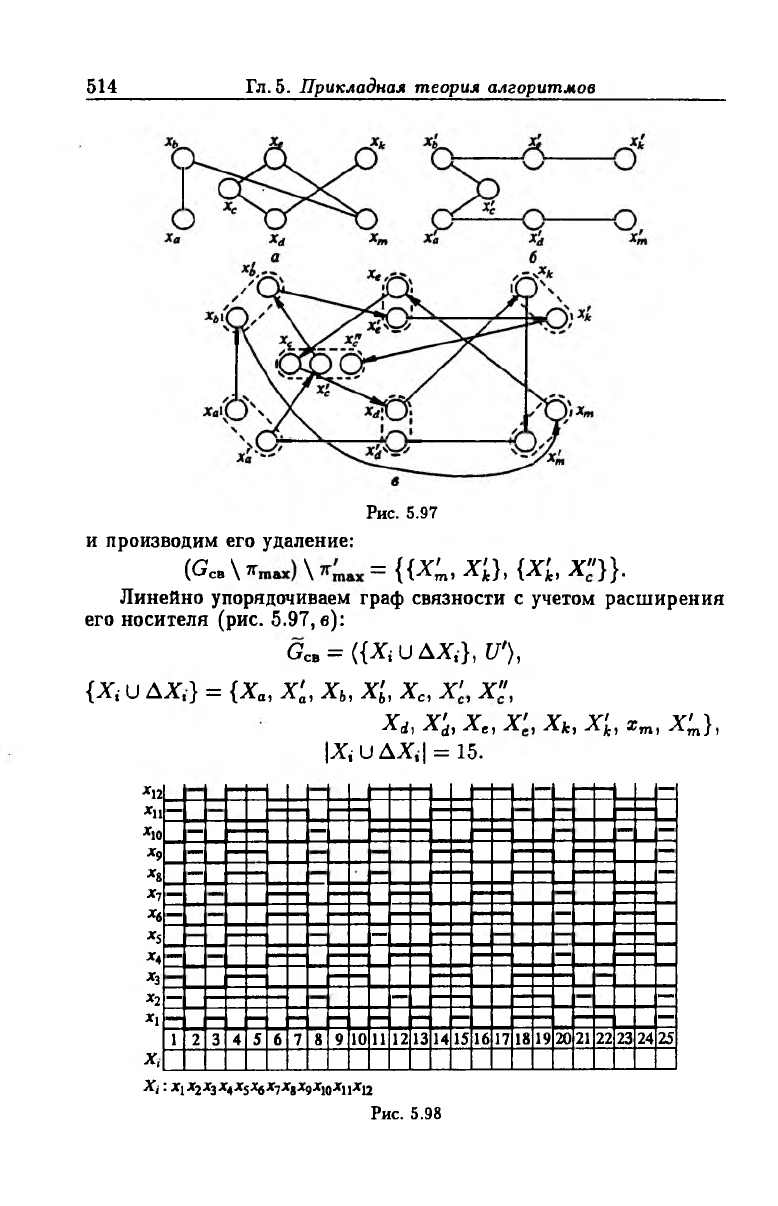
Рис. 5.97

и производим его удаление:

(<?„ \ к \ = { д а , х з , д а , х"}}.

Линейно упорядочиваем граф связности с учетом расширения

его носителя (рис. 5.97, в):

Gcb = ({Xi U ДХ,}, U'),

{Xi U ДХ,} = {Х0, х :, Хь, Х'ь, Хс, X', X ",

xdt x'd, х е, х', Хк, Х'к, хт, х;},

|Xi U ДХ,| = 15.

*12

*11

* 10

х9

* 8

— -■

—

— — —

—

— —

—

— —

—

— —

— — —

—

4 5 6

13 14 15

18 19 20

21 22

23 24 25

X,: Д^Д^З *4*5*6*7***9*10*11*12

Рис. 5.98

§5.11. Оценка динамики логических структур 515

При реализации линейно упорядоченного графа связности GCB =

= ({Л,- U ДХ,}, U') имеем 14 ребер, 15 вершин, 7 из которых

соответствуют повторениям входных векторов.

Функционалом качества у>КЛЧ решения этой задачи будем счи

тать число, равное количеству повторений входных векторов, т. е.

¥>кач = т|п|{дх,}_,|.

При <ркач = 0 граф связности является как эйлеровым, так и га

мильтоновым.

Если эйлеровость графа характеризуется наличием и распре

делением вершин с нечетными степенями, то эффективное опреде

ление гамильтоновости графа является открытой проблемой. По

этому предложим приближенное, но с практической точки зрения

оптимальное решение этой задачи.

Линейно упорядоченный граф связности определяет как объем

памяти V„, так и время выполнения Т„ входной сигнальной про

граммы при моделировании аномалий динамических свойств ИС:

Vn = (|Х,- U ДХ,| — 1) • квж,

Т„= (| Х ,и Д Х ,| -1 ).Т мод.1,

где ТМОд.1 — время моделирования одного переключения —> Xj.

Линейное упорядочение графа связности является третьим (за

вершающим) этапом синтеза входной сигнальной программы

(ВС-программы). Синтезированная ВС-программа для нейрон

ной сети (см. рис. 5.89) и построенных решетчатых интервалов

J[ — J '30 представлена на рис. 5.98.

Для оценки переходного процесса в ИС предложим число

вую характеристику в виде соответствующего функционала

ip(Ta(Xi, Xj)), учитывающего распределение трасс, функциональ-

—1 —1 —

—

—1 —|

—

— — —

—

— — —

—

|—

28 29 30

38 39 40 41 42

43 44 45 46

50 51

Продолжение рис. 5.98

516

Гл. 5. Прикладная теория алгоритмов

ные и топологические свойства ИС и временной дебаланс пере

ключаемых цепей в ИС:

<p(T,(Xi, Xj)) = шах Tig fj2 f(T ( X {, X,•)) х

х (H(Xit X j)!)-1 • A rmax(J(Xi, X j) ) ) ) , (5.24)

s = 1, 2, ..., тп.

Здесь:

f(T(Xi, X j)) — частота (количество) цепей (X,, X j) решет

чатого интервала J = [X,-, X j], для которого функция риска сбоя

s-ro выходного канала R„(Xi, X j) = 1 — количество трасс;

Н(X,-, X j) — расстояние по Хеммингу между точками X,- и X j

в булевом ^вх,-мерном пространстве;

&Tmax(J(Xi, X j)) — максимальный временной дебаланс це

пей при переключении векторов X,- X j для s-ro выходного эле

мента ИС,

Д т-п .а*№ , = max(rmax(Tjt(X,-, X j)) - rmin(T,(X„ X j))),

где

w C zM X ,-, X j)) — максимальное время задержки переключе

ния входного канала rmax = m axr3afl(xa), а = 1, 2, ..., fcBX>;

ТзлЯ(ха) — время задержки канала ха s-ro выходного элемента

для к-й трассы решетчатого интервала J(X,-, X j);

rmin(Tjt(Xi, X j)) — минимальное время задержки переключе

ния входного канала тт \а = mjn ^ „ (а ^ ), /? = 1, 2, . . &BXj,

s-ro выходного элемента для к-й трассы решетчатого интервала

J(Xi, X j);

m — количество выходных каналов логической структуры.

В функционале (5.24) частота трасс и соответствующие им

расстояния по Хеммингу определяют функциональные свойства

выходных элементов, дебаланс цепей — топологические свойства

всей логической структуры.

Значение функционала (5.24) мажорирует относительную за

держку на входных каналах выходных элементов ИС. Для нор

мального функционирования время смены входных векторов (ре

активность ИС) не должно превышать ш ах(Дгтах(7(Х,-, X j))) ,

j,» *

т. е. временную задержку для наихудшего случая переключений.

Предложенный функционал (5.24) позволяет оценить переход

ные процессы на этапе логического проектирования.

§5.11. Оценка динамики логических структур 517

Чем меньше значение функционала (5.24), тем меньше пере

ходной процесс влияет на функционирование логической струк

туры.

На основе предложенного функционала оценки качества логи

ческого проекта (5.24), оценим переходной процесс в нейронной

сети (см. рис. 5.85, 5.89-5.92).

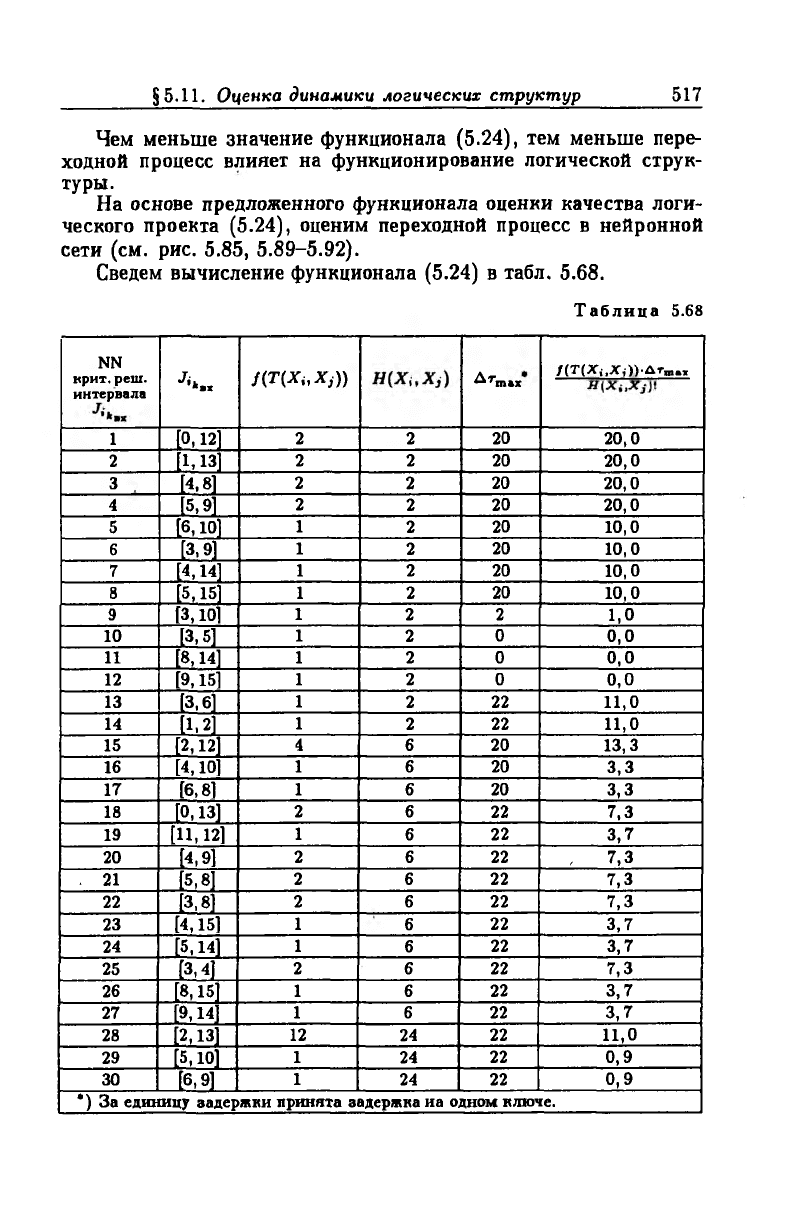
Сведем вычисление функционала (5.24) в табл. 5.68.

Таблица 5.68

крит. реш.

интервала

Ji*,x

/ ( Т ( * ,* у ) )

^ тт и

/(Г№ ,х())-Дгт „

[0,12] 2 2

20,0

1 1 . 13]

2 2 20 20,0

[4. 8]

20,0

[5, 9]

20,0

5 [6,10]

10,0

6 [3. 9]

10,0

7 [4, 14]

1 2 20 10,0

[5, 15]

1 2

10,0

[3,101

2 2

1,0

13, 5]

0,0

[8, 14]

1 2 0 0,0

[9, 15]

1 2 0 0,0

[3, 6]

2 22 11,0

[1.2]

2 22 11,0

15 [2,12]

6 20 13,3

[4,101

1 6 20

3,3

[6,81

1 6 20 3,3

[0, 13]

2 6

22 7,3

[П , 121

3,7

[4,91

2 6 22

, 7,3

. 21 [5, 8]

2 6 22 7,3

[3.81

2 6 22 7,3

[4,151

3,7

[5, 14]

22 3,7

[3,41

2 6 22 7,3

[8, 15]

1 6

22 3,7

27 [9, 14]

1 6 22

3,7

[2, 13]

12 24 22

11,0

[5, 10]

22 0,9

[6,91

24 22

0,9

*) За единицу задержки принята задержка иа одном ключе.

518

Гл. 5. Прикладная теория алгоритмов

Суммируем элементы последнего столбца и, логарифмируя сум

му, получаем

¥>кан(5) = m axA g Xj)) • (H(X„ Xj)\)~l x

X Дгтах • T(Xi, X j)j ) = lg 230, 7 * 2,2.

Минимизация функционала (5.24) осуществляется с помощью

уменьшения дебаланса активизируемых цепей. Для нейронных

сетей гексагональной структуры, работающих в условиях субми-

кронной технологии, нулевой дебаланс активизируемых цепей

достигается совместным решением систем уравнений для разре

шенных и запрещенных квазипорогов всех нейронов сети путем

соответствующего согласования весов синапсов: суммы весов си

напсов нейронов, образующих активизируемую цепь, должны быть

равными для каждой цепи.

§ 5.12. Семантическое проектирование

скоростной транспортной сети большого города

Повышение пропускной способности, увеличение скорости со

общения и безопасности движения транспорта и пешеходов в боль

ших городах является важной и острой проблемой в современном

градостроительстве. Ее решение связано не только с большими

капитальными затратами, но и с проблемой сохранения истори

ческих памятников и памятников культуры. При этом ввод маги

стралей с большой пропускной способностью ставит проблему раз

работки принципа оптимальной трассировки скоростных дорог.

Дорога называется скоростной, если мощность транспортного

потока, который она реализует, не меньше одного экипажа в се

кунду в одном направлении. Такой поток называется скорост

ным.

Идеальным принципом управления скоростными потоками яв

ляется принцип непрерывного движения на магистралях типа ско

ростной дороги, т. е. управление “без управления”, когда потоки

не пересекаются, а “вливаются” и “разливаются”. Исходной ин

формацией синтеза сети скоростного движения является граф кор

респонденций Gс = (К , Uc), каждая вершина которого взаимо од

нозначно соответствует транспортному району и вершины и,-, Vj

связаны ребром {и,-, Vj} 6 Uc, если плотность транспортного по

тока в “час пик” не меньше 3600 экипажей в одном направлении.

Транспортные потоки прогнозируются на основе использования

парной и множественной регрессии.

Рассмотрим проектирование транспортной сети скоростного

движения, представив транспортную сеть большого города как объе

динение сети, реализующей скоростные потоки и построенной на

$ 5.12. Семантическое проектирование скоростной

519

основе частичного квазиупорядочения, и сети, реализующей осталь

ные потоки и построенной на основе кратчайших остовов. При

этом скоростное движение является свободным движением, ско

ростные потоки не пересекаются (друг с другом и с пешеходными

потоками). Управление во второй сети осуществляется, как обычно,

с помощью светофоров.

Преобразование графа скоростных потоков Gc — (Vc, Uc) в сеть

скоростного движения Sc = (Vc, <) заключается в частичном ква

зиупорядочении графа Gc, Gc Sc- Если при частичном упорядо

чении некоторое подмножество преобразуется в путь, а все такие

подмножества — в диаграмму Хассе, то при частичном квазиупо

рядочении они преобразуются соответственно в гамильтонов кон

тур и цунг.

При этом очевидно, что запрещенные фигуры относительно

предиката частичного упорядочения Ро(Фа) Фь) являются запре

щенными фигурами относительно предиката частичного квазиу

порядочения Po(Gc, Sc), и наоборот. Поэтому методы частичного

упорядочения с успехом могут быть использованы и при транс

портной интерпретации.

Временные затраты, отведенные в данном городе в “час пик”

(обычно это время равно 45 мин) определяют ограничения, кото

рые рассматриваемое преобразование Gc —> 5С сводят к преобра

зованию вида Фо —> 5С:

Фо = (М,52, ..., 5n), M = VC.

Сигнатура модели Фа представляет собой полные подграфы

Fi = (VJ, Ui) графа Gc, удовле*воряющие следующему условию:

время езды от произвольной вершины v е до середины каждого

гамильтонова контура любого из этих подграфов Fi не превышает

предельных временных затрат, отведенных в “час пик”.

Семантика этого преобразования также определяется предика

том частичного упорядочения.

Для проектирования сетей скоростного движения предложим

следующую стратегию.

1. В графе корреспонденций Gc = (V, (U, Р)), матрица смеж

ности которого имеет вид [sij]|K|x|K|i

с, если P(vi, Vj) > 3600 эк./ч,

1, если 150 эк./ч < Р(t/,-, Vj) < 3600 эк./ч,

0, если P[v{, Vj) < 150 эк./ч,

P(vi, Vj) — плотность транспортного потока между i-м и j -м транс

портными районами.

2. Формируем сигнатуру модели Ф0 выделением всех полных

подграфов Fi = (Vi, Ui) графа Gc, удовлетворяющих временному

Sij =

520

Гл. 5. Прикладная теория алгоритмов

ограничению (время езды от произвольной вершины v G V* до се

редины каждого гамильтонова контура подграфа F, не превышает

времени, отведенного на езду в “час пик”).

3. Упрощением модели Фа Фа -> Фа (Ро(Фа> Фь) = 1), опре

деляются запрещаемые потоки, которые реализуются транзитно

через другие транспортные районы. В результате упрощения мо

дели Фа ее функциональная связность уменьшается настолько, что

возможно частичное квазиупорядочение модели Фа.

4. Частично квазиупорядочиваем модель Фа. Удаляем все за

мыкающие дуги. Полученные гамильтоновы контуры, соответ

ствующие словам модели Фа, сопоставляем скоростному кольцу,

на котором не стоит ни один светофор и который не пересекает ни

один поток. Полученная модель Фь определяет сеть скоростного

движения S.

Маршрут из одной вершины в другую вершину сети Sc реа

лизуется набором соответствующих отрезков полученных колец

непрерывного движения. Съезд с одного кольца на другое осу

ществляется стандартным образом.

Проиллюстрируем предложенную методику построением

транспортной сети крупного города. Пусть в транспортном разделе

генерального плана города имеется граф корреспонденций, ребра

которого взвешены плотностью транспортных потоков. Матрица

смежности этого графа имеет вид

1 2 3 4 5

6 7 8

10 11 12 13 14 15 16

—

с с с с с с 0

0 0 0 0 0 0 0 0

—

с с

0 1

0 0

0 1 1 0 0 0 0 0

с с

—

с с

0 1

0 0 0 0 1 1 3

с с с

—

0 0

0 0 0 0 0

1 1 0 0 0

с 0 с

—

с с с 0 0 0 0 0 0 0 0 0

1 0 0

—

1 0 1 0 0 0 0

0 0

1 1

с с

—

1 0 0 0 0

0 1 1

0 7

0 0

—

1 0 0 0 0 0 0 0 0

0 0

0 0 0 1 0 0 0 0 0 0 0 1 9 '

0 0 0 0 0 1 0 0 0

—

1 0 0 0 0 0 0

0 0 0 0 0 0 0

—

0 0

0 0 0 0

0 1 0

0 0 0 0 0 0 0

—

0 0 0

0 0 1 0 0 0 0 0 0 0

—

0 0 0 0

0 0 0 1

1 0 0 0 0 0 0

—

1 0 0

0 0 0 0 0 0

0 0 0 1

—

1 0

0 0

0 0 0 0 0 0 0

0 0 0 0 1

—

0 0 1 0 0 0 0

0 0 0 0 0 0 0

Согласно предложенной стратегии выделяем частичный под

граф, соответствующий скоростным потокам. Матрица смежности