Горбатов В.А. Фундаментальные Основы Дискретной Математики. Информационная Математика

Подождите немного. Документ загружается.

§ 5.9. Синтез функциональной декомпозиции

__________481

т. е. получили декомпозицию исходной функции от шести пере

менных в виде системы одной функции от пяти переменных, двух

функций от четырех переменных и двух функций от трех перемен

ных Внешняя функция F не удовлетворяет введенным ограни

чениям и ее необходимо декомпозировать дальше. Такой резуль

тат получен при последовательном способе поиска декомпозиции.

Более оптимальное решение получим при параллельном способе

поиска. Для этого расширение пространства P(<pi, ^ 2) до про

странства P{<fi, <Р2, Х4) спроектируем на расширение простран

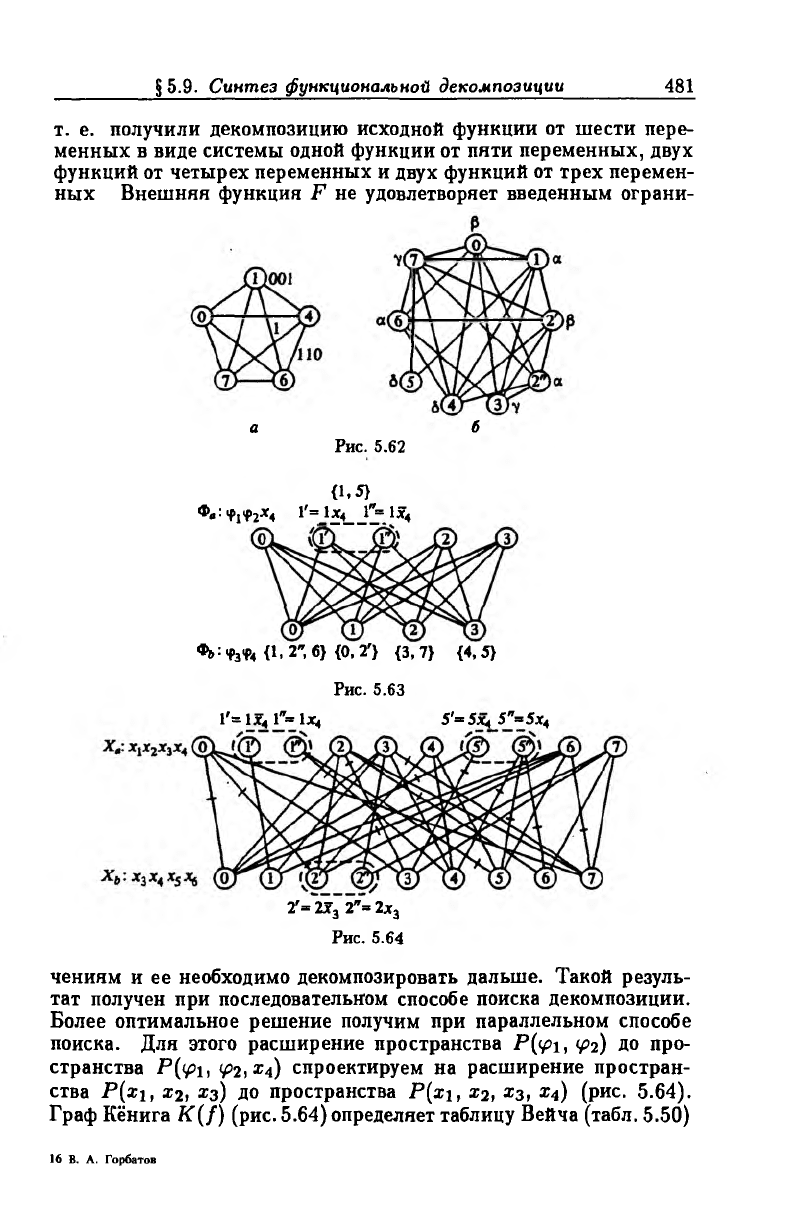
ства P(xi, х2, хз) до пространства Р{х\, х2, х3, х4) (рис. 5.64).

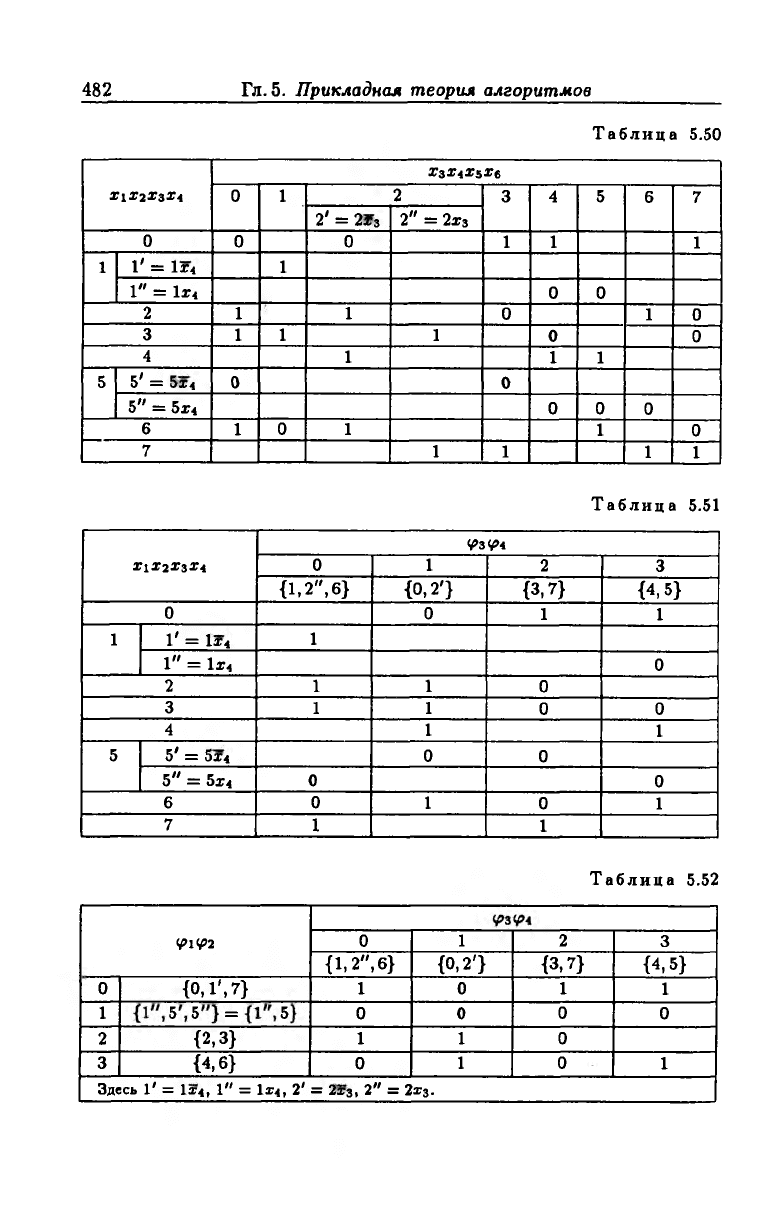
Граф Кёнига К (/) (рис. 5.64) определяет таблицу Вейча (табл. 5.50)

Рис. 5.62

{1.5}

Ф.:*,¥2*4 l'=Ji4_Jl=l*4

Фб: ¥з*4 {1. 2", 6} {О, У) {3, 7} {4, 5}

Рис. 5.63

1'= 1У« Г- 1*4

5'= 5х4 5"= 5х4

2'= 273 2"= 2х3

Рис. 5.64

16 В. А. Горбатов

482 Гл. 5. Прикладная теория алгоритмов

Таблица 5.50

X 1X 2 X 3 X 4

13 X 4 X 5 X 6

0 1

3 4 5

6 7

2' = 2х3 2" = 2х3

0 0

1 1

1 1' = 1 Х4 1

1" = 1х4

0 0

1 1

1 1 1

1 1

5 5' = 5х4

5" = 5x4

0 0

0 1

1 1

Таблица 5.51

X1X2X3X4

V3V4

0 1

{1,2", 6}

{0, 2'}

{3,7}

{4,5}

1' = 1X4

1" = 1X4

2 1 1

1 1

0 0

5 5' = 5X4

5" = 5X4

6 0

0 1

Таблица 5.52

VIV2

2 3

{1,2", 6}

{0,2'} {3,7} {4,5}

{0,1',7}

1 0 1

СЛ

0 0

2 {2,3}

1 1 0

{4,6} 0

1 0

Здесь 1' = 1*4, 1" = 1*4, 2' = 2хз, 2" = 2х3.

§5.10. Семантическое проектирование нейронных сетей 483

с учетом расширения пространств Р(Ха), Р(Хь), при котором га

рантируется размерность функций, декомпозирующих исходную

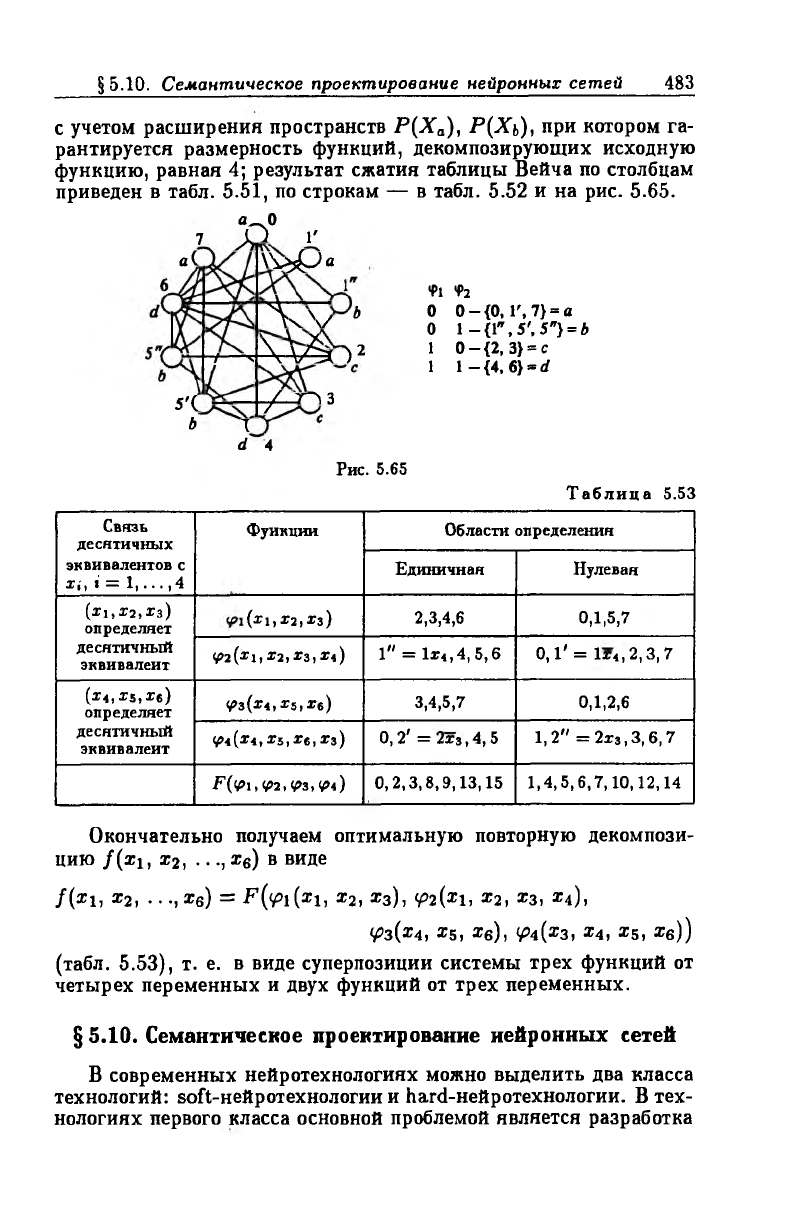
функцию, равная 4; результат сжатия таблицы Вейча по столбцам

приведен в табл. 5.51, по строкам — в табл. 5.52 и на рис. 5.65.

а .

7 А

У 1'

a t

V v ^ J e

Ч> l

Л о ч / *

0 0 — {0. 1', 7} = a

1 - {Iя , 5', 5"} = b

\ v ^ x ')2

1 0 — {2, 3} = с

/ >

1 —{4. 6}»rf

5'С

.уУглз

ь Т

d 4

Рис. 5.65

Таблица 5.53

Связь

десятичных

эквивалентов с

Xi, i = 1,. - ., 4

Функции

Области определения

Единичная

Нулевая

(Х1,Х2 ,ХЗ)

определяет

десятичный

эквивалент

l(xi,X2 ,X3 ) 2,3,4,6

0,1,5,7

<?2 (XI,X2 , Хз,Х4)

1" = 1x 4, 4, 5,6

0 ,1' = 1х4,2 ,3,7

(Х4 ,Х$,Х6 )

определяет

десятичный

эквивалент

4>з(х4,ха,х6)

3,4,5,7

0,1,2,6

tpt(Xi,X 5,Гб,Гз)

0, 2' = 2х3, 4,5

1, 2" = 2хз, 3, 6, 7

F((fil,V2 ,V3 ,V4 )

0, 2, 3, 8, 9, 13,15

1, 4, 5, 6, 7, 10, 12,14

Окончательно получаем оптимальную повторную декомпози

цию /(хь х2, ..., х6) в виде

/(*1, х2, ...,х 6) = F((pi(x b х2, х3), cp2(xi, х2, х3, х4),

^з(®4| ®5i ®б)) ^4(^3) ®4) ®5i ®б))

(табл. 5.53), т. е. в виде суперпозиции системы трех функций от

четырех переменных и двух функций от трех переменных.

§ 5.10. Семантическое проектирование нейронных сетей

В современных нейротехнологиях можно выделить два класса

технологий: soft-нейротехнологии и hard-нейротехнологии. В тех

нологиях первого класса основной проблемой является разработка

484

Гл. 5. Прикладная теория алгоритмов

стратегий обучения и самообучения нейронных сетей, включаю

щих в себя синтез сценариев обучения. Эти технологии особенно

важны при решении неформализованных задач при наличии

зашумленной, противоречивой, неполной входной информации.

Такими задачами являются задачи распознавания, классифика

ции, прогнозирования, краткосрочного предсказания, которыми

изобилуют финансовая и оборонная области деятельности чело

века.

В hard-технологиях, реализованных в виде нейроБИС, нейро-

платакселераторов и работающих, как правило, в субмикронном

диапазоне, одной из главных проблем является проблема разложе

ния произвольной булевой функции /(хi, х2, ..., хп) в декомпози

цию функций от четырех-пяти переменных. Современный уровень

технологий в электронной промышленности России и США по

зволяет выпускать четырехсинаптические нейроны, а в Японии —

пятисинаптические нейроны при их цифровой реализации.

Рассмотрим проектирование четырехсинаптической нейрон

ной сети на однородных нейронах гексагональной структуры,

реализующей булеву функцию /(хi, х2, хв) (табл. 5.54).

Таблица 5.54

Единичная область функции

f(xu x 2,...,х6)

Нулевая область функции

f(xi,x2,...,x6)

-00100,

0 0 0- 11

00 0 0 -0 ,

—ОНО—

0 - 1001, 010 - 10

0 - 1100, 010-11

01 - 010,

-10010 101 - 00, 1011 - 0

01100-,

ОНО - 0 01 - 111,

110001

1 - 0010,

10010- 101011, -10111

1100 - 0,

00-111

-11010, 1 - 0101

11 - 010, 11101—

111 -11,

11111—

Представим исходной пространство Р(хi, х2, ..., хв) в виде де

картова произведения пространства размерности 3:

Р(хи Х2, ...,Х6) = Ра(хи х2 , Х3) X Рь{х4, Х5, Х6),

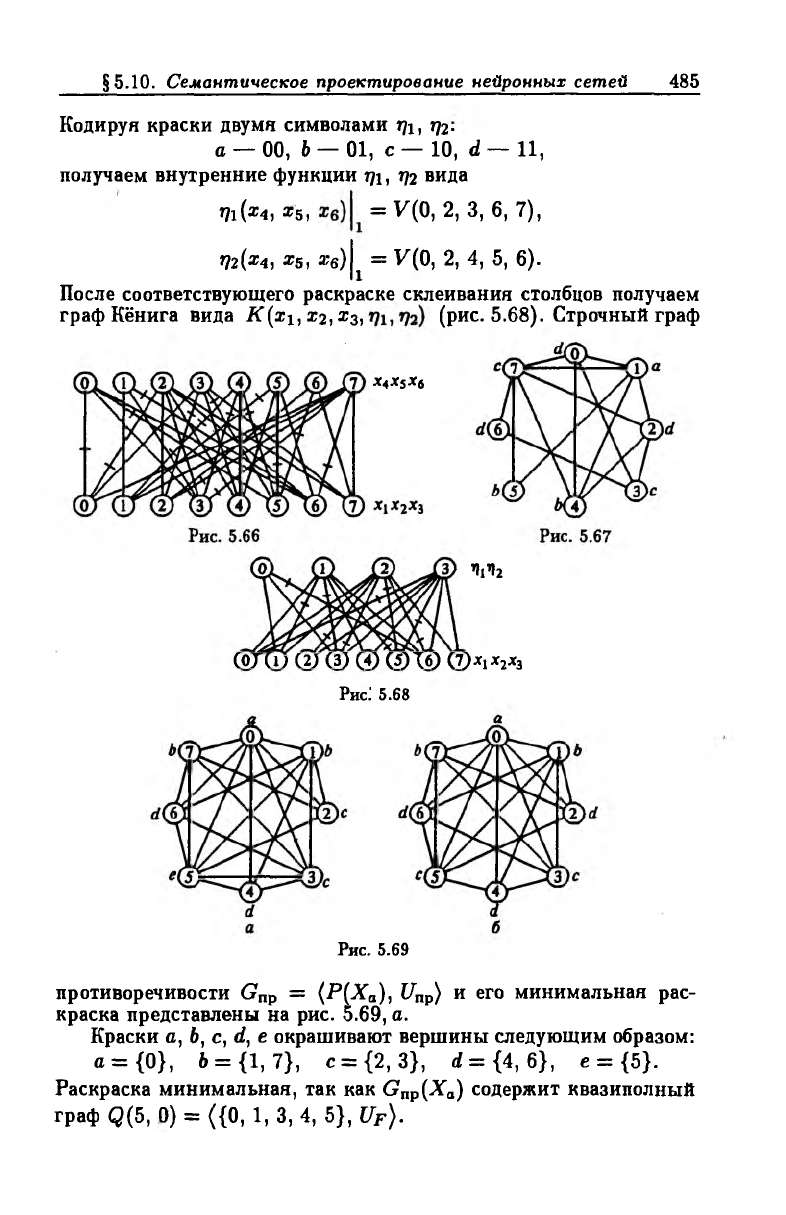
и зададим исходную функцию в виде графа Кёнига K (f)

(рис. 5.66).

Столбцевой граф противоречивости Grmnp(Xj,) имеет вид

рис. 5.67. Граф G>mnp(X(,) содержит квазиполный подграф Q (4,0);

Grm„P(Xb) D Q(4, 0), Q(4, 0) = ({1, 2, 4, 7}, UF).

Следовательно, его хроматическое число равно 4 и минимальная

раскраска имеет вид а = {1}, Ь = {4, 5}, с = {3, 7}, d = {0, 2, 6}.

§5.10. Семантическое проектирование нейронных сетей 485

Кодируя краски двумя символами щ, щ-

а — 00, b — 01, с — 10, d — 11,

получаем внутренние функции г]i, щ вида

щ(х4, *в, = V(0, 2, 3, 6, 7),

m(x4, x5i а*)^ = F(0, 2, 4, 5, 6).

После соответствующего раскраске склеивания столбцов получаем

граф Кёнига вида K (x i,i2,x3, (рис. 5.68). Строчный граф

*4*5*6

4in2

СОТСи C2J (3) (4) (S)J6) (7)xlx2x3

Рис! 5.68

Рис. 5.69

противоречивости Gnp = (Р(Ха), Unр) и его минимальная рас

краска представлены на рис. 5.69, а.

Краски а, 6, с, d, е окрашивают вершины следующим образом:

а = {0}, 6 = {1,7}, с = {2,3}, d = {4, 6}, е = {5}.

Раскраска минимальная, так как Gnp(Xa) содержит квазиполный

граф Q(5, 0) = ({0, 1, 3, 4, 5}, UF).

486

Гл. 5. Прикладная теория алгоритмов

3'=3?! З'-З*!

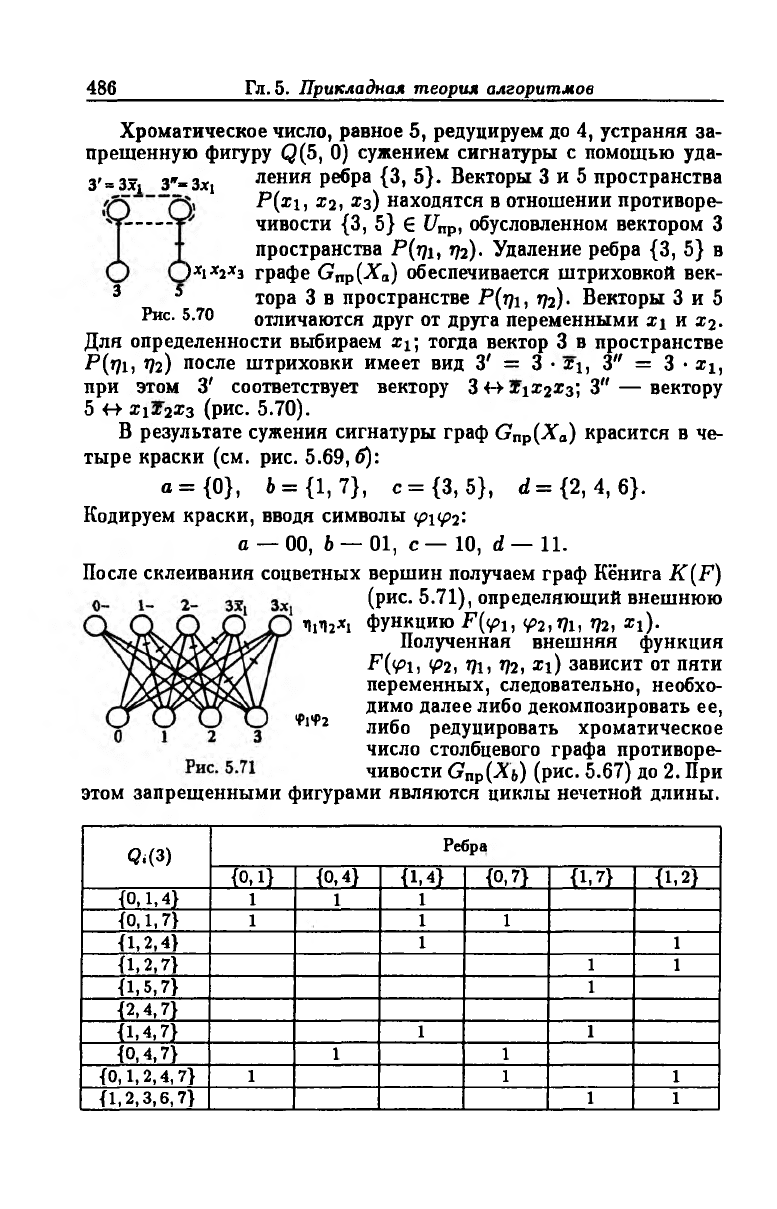
Хроматическое число, равное 5, редуцируем до 4, устраняя за

прещенную фигуру Q(5, 0) сужением сигнатуры с помощью уда

ления ребра {3, 5}. Векторы 3 и 5 пространства

Р{х 1, Х2, хз) находятся в отношении противоре

чивости {3, 5} € иар, обусловленном вектором 3

пространства Р(щ, г)2). Удаление ребра {3, 5} в

)*1*2*3 графе Gnp(Xa) обеспечивается штриховкой век-

3 5 тора 3 в пространстве Р(щ, %). Векторы 3 и 5

Рис. 5.70 отличаются друг от друга переменными x i и х 2.

Для определенности выбираем xi; тогда вектор 3 в пространстве

P(V 1) V2) после штриховки имеет вид 3' = 3 • xi, 3" = 3 • xit

при этом 3' соответствует вектору 3 «-> Х1Х2Х3; 3м — вектору

5 <-)■ x ix 2x3 (рис. 5.70).

В результате сужения сигнатуры граф Gnp(Xa) красится в че

тыре краски (см. рис. 5.69,6):

а = {0}, Ь = { 1,7}, с = {3,5}, d = { 2 ,4 ,6 } .

Кодируем краски, вводя символы ipiip2:

а — 00, 6 — 01, с — 10, d — 11.

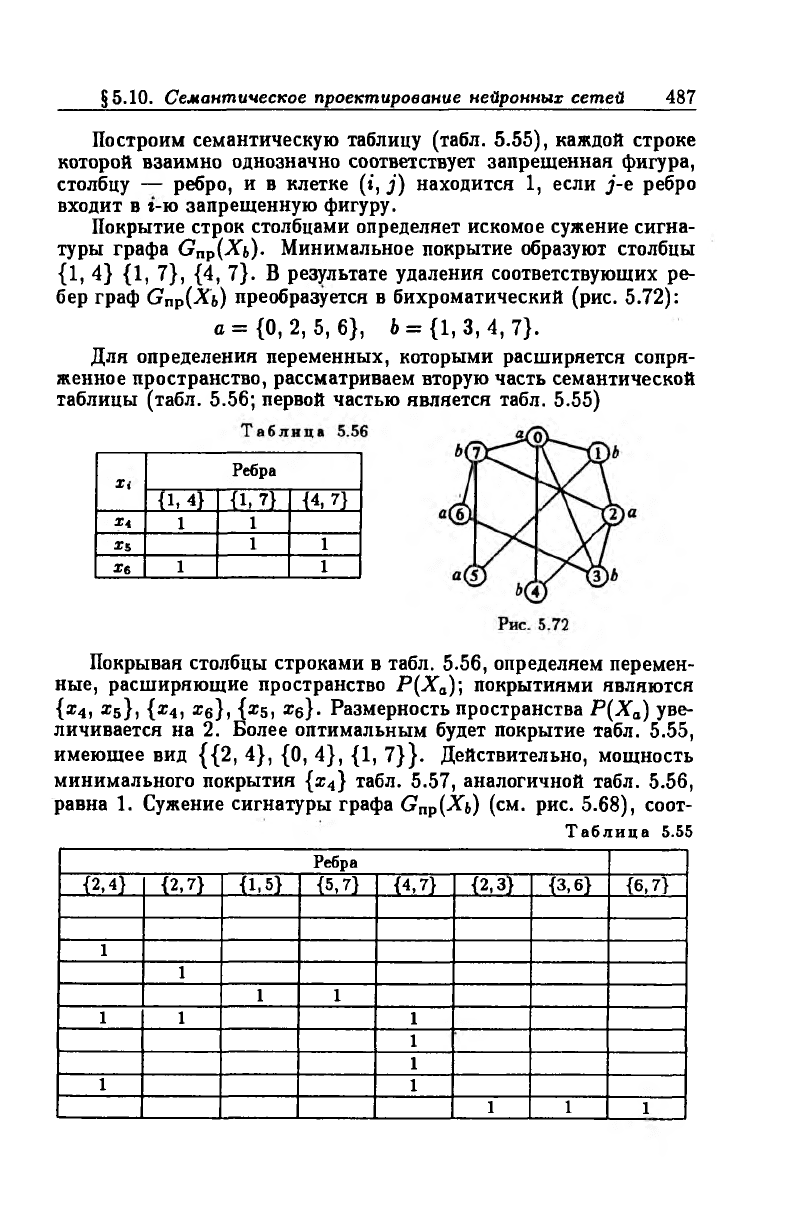
После склеивания соцветных вершин получаем граф Кёнига К (F)

(рис. 5.71), определяющий внешнюю

4l42*l ФУНКЦИЮ F(y> i, ip2,m , Г]2, x i ) .

Полученная внешняя функция

jP(^1 , <Р2 , Щ, Т)2 , Xi) зависит от пяти

переменных, следовательно, необхо

димо далее либо декомпозировать ее,

либо редуцировать хроматическое

число столбцевого графа противоре

чивости Gnp(-Xb) (рис. 5.67) до 2. При

этом запрещенными фигурами являются циклы нечетной длины.

Ч>1Ч>2

Qi( з)

Ребра

{0,1}

{0,4}

{1,4}

{0,7}

{1,7}

{1,2}

{0,1,4}

{0,1,7}

1 1 1

0,2,4} 1

{1,2,7} 1

{1,5,7} 1

{2,4,7}

{1,4,7}

1 1

{0,4,7}

1 1

{0,1,2,4, 7} 1 1

{1,2,3,6,7}

1 1

§5.10. Семантическое проектирование нейронных сетей 487

Построим семантическую таблицу (табл. 5.55), каждой строке

которой взаимно однозначно соответствует запрещенная фигура,

столбцу — ребро, и в клетке (i, j) находится 1, если j-e ребро

входит в г-ю запрещенную фигуру.

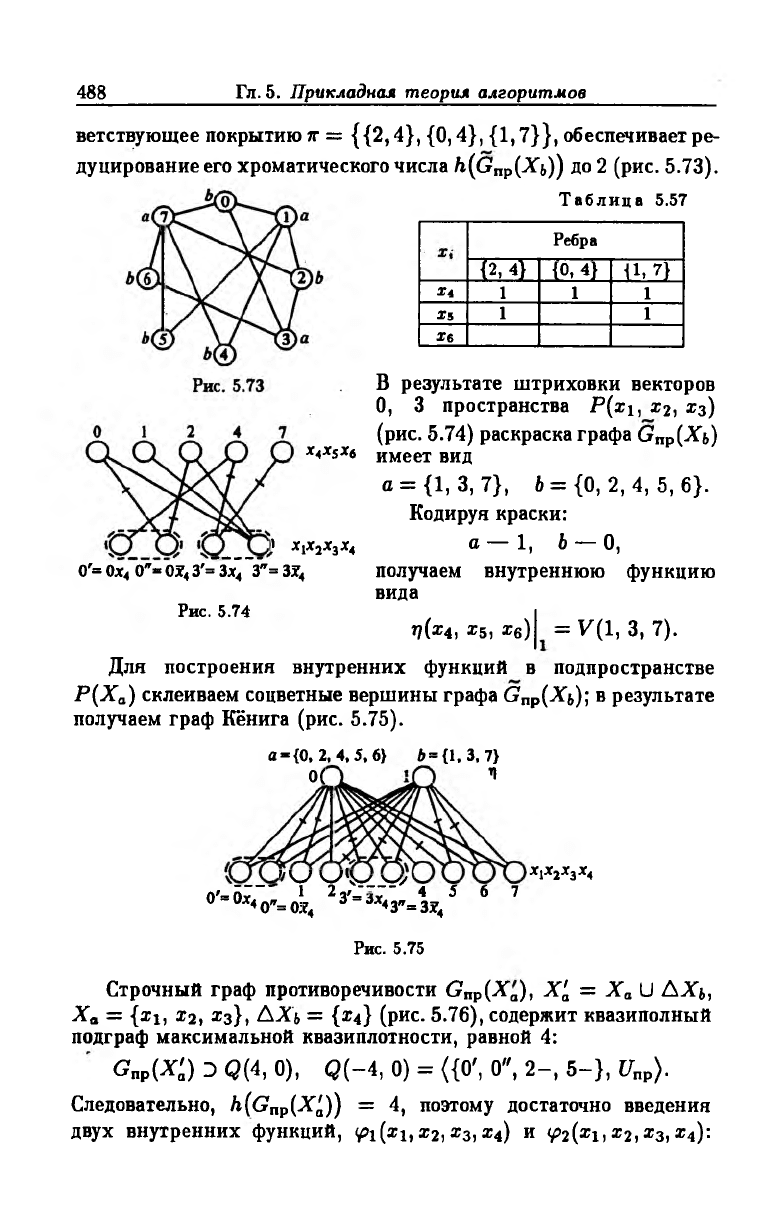
Покрытие строк столбцами определяет искомое сужение сигна

туры графа Gnp(Xb). Минимальное покрытие образуют столбцы

{1, 4} {1, 7}, {4, 7}. В результате удаления соответствующих ре

бер граф Gпр(-Хь) преобразуется в бихроматический (рис. 5.72):

а = {0,2, 5, 6}, 6 = {1,3, 4, 7}.

Для определения переменных, которыми расширяется сопря

женное пространство, рассматриваем вторую часть семантической

таблицы (табл. 5.56; первой частью является табл. 5.55)

Ребра

{1, 4}

{1.7} {4, 7}

Хб

1 1

Покрывая столбцы строками в табл. 5.56, определяем перемен

ные, расширяющие пространство Р{Ха)\ покрытиями являются

{х4, х5}, {х4, х6}, {х5, х6}- Размерность пространства Р{Ха) уве

личивается на 2. Более оптимальным будет покрытие табл. 5.55,

имеющее вид {{2, 4}, {0, 4}, {1, 7}}. Действительно, мощность

минимального покрытия {х4} табл. 5.57, аналогичной табл. 5.56,

равна 1. Сужение сигнатуры графа Gnp(Xb) (см. рис. 5.68), соот-

Таблица 5.55

Ребра

{2,4} {2,7}

{1,5}

{5,П

{4,7} {2,3}

{3,6} {6,7}

1 1

488

Гл. 5. Прикладная теория алгоритмов

ветствующее покрытию ж = {{2,4}, {0,4}, {1,7}}, обеспечивает ре

дуцирование его хроматического числа h(Gnp(Xb)) до 2 (рис. 5.73).

Таблица 5.57

Ребра

{2, 4}

(0, 4}

I1. 7)

1 1

Хб

В результате штриховки векторов

О, 3 пространства Р(хi, х2, хз)

(рис. 5.74) раскраска графа Gnp(Xb)

x*xsxt имеет вид

а = {1,3, 7}, Ь = { 0 ,2 , 4, 5, 6}.

Кодируя краски:

а — 1 , 6 — 0 ,

получаем внутреннюю функцию

вида

Т)(х4, Х5, Хб)| = V (l, 3, 7).

Для построения внутренних функций в подпространстве

Р(Ха) склеиваем соцветные вершины графа Gnp(^f,); в результате

получаем граф Кёнига (рис. 5.75).

II XiX2X3X4

0'= 0хА 0"- ОЗГ4 3'= Зх4 3"= щ

Рис. 5.74

а~{0, 2,4, 5,6}

*={1.3, 7}

* 1* 2*3 *4

____

’у V ’ 'V'WiJSr*' . f _

ft'= O r 1 2 X= 4 5 6 7

o- Ox4 0"=0jf4 3 3^зя=зг4

Рис. 5.75

Строчный граф противоречивости Gnp(-X'a), Х^ = X a U АХь,

Ха = {®i, х2, а:з}| Д-Хь = {^4} (рис. 5.76), содержит квазиполный

подграф максимальной квазиплотности, равной 4:

Gnp(X'a) D 0 (4, 0), 0 ( - 4 , 0) = ({O', 0", 2 -, 5 -} , Unp).

Следовательно, h(G„p(X'a)) = 4, поэтому достаточно введения

двух внутренних функций, <рг(хх, х2, х3, х4) и V>2(si,a;2, £3, 2:4):

§5.10. Семантическое проектирование нейронных сетей 489

[log2 fc(GnpTO)] = 2. Кодируем краски а, Ь, с, d (табл. 5.58)

и получаем

, V / 1 на 0', 3', 3", 5 -, 7 -

ф и х2, хз, х4) = 1 0 на 0„’ 11 ) 2’_ 1 _

, ч /1 на 2 -, 4 - , 3', 5 -, 6 -,

ф \ , Х2 , Х3, х4) - | о на 0', 0", 1 -, 3", 7 - .

Согласно проведенной раскраске Gnp(X'a) (см. рис. 5.76) склеиваем

соцветные вершины; в результате получаем табл. 5.59, определяю-

Таблица 5.58

Краски

а = {0», 1-} 00

Ь = {2 - 4 -, 6 -}

СО

<*={3', 5—}

Таблица 5.59

Рис. 5.76

Ч>1Ч> 2

0 1

1 1 0

2 1 1

щую внешнюю функцию F оптимальной повторной декомпозиции

исходной функции f(xi, х2, ..., Хб):

f(x 1, х2, хб) =

= F(tpi{xu Х2, Х3, X4),V>2(X!, Х2, Х3, Х4), Г)(х4, х5, х6)),

{xi, х2, х3, х4} П {х4, х5, х6} = {х4}.

Внешняя функция F(<p\, <р2, v) имеет вид

1,<Р2, ^ = ^(1 , 2, 4, 5).

В результате исходная булева функция от шести переменных

представлена в виде повторной декомпозиции двух функций (щ

и (р2) от четырех переменных и двух функций (F и Т)) от трех

переменных.

Вторым способом штриховки является способ, основанный на

введении специальных переменных штриховки {хШТ1}. Выше

были найдены два покрытия ж\ и ж2 (см. табл. 5.55):

*1 = {{1.4}, {1,7}, {4,7}}, *г2 = {{2,4}, {0,4}, {1,7}}.

490

Гл. 5. Прикладная теория алгоритмов

Для определения размерности вектора штриховки строим граф

зацепления <2эац = (У, излц, X )), являющийся подграфом соот-

Рис. 5.77

ветствующего графа противоречивости. Для покрытия граф за

цепления (рис. 5.77, а) имеет вид

С'зац ~ (■V., (С/зац, * ) ) ,

V = { 1 , 4 , 7}, С/зац = { {1 , 4 } , {1 , 7}, { 4 , 7}},

для покрытия я-2 — вид (рис. 5.77,6)

<?зац=({0, 1 ,2 ,4 , 7}, (С/зац, X)),

t u = {{0, 4}, {2, 4}, {1,7 }}.

Двоичный логарифм хроматического числа графа зацепления

определяет минимальное значение размерности вектора штрихов

ки ХШТ, значение которого для равно 2:

|Хшх| = [log2 ^(G3aH(7Ti))] = [log2 3] = 2,

а для 7г2 — 1. Выбираем второе покрытие.

Минимальная раскраска вершин графа G3au(7r2) имеет вид

а = { 0 ,2 , 7}, Ь = { 1,4}.

Кодируя краски о — 0, 6 — 1, получаем значение вектора штри

ховки Хшт, задаваемого функцией

<Aiit(s 4, S5, х6) = j Q н а 0| 2| у

Векторы 0, 1, 3 пространства Р(хi, х2, Хз), определяющие зацеп

ления векторов 0, 1, 2, 4, 7 пространства Р(х4, х5, х6), штри

хуются согласно раскраске G m ,,^ )) как показано в табл. 5.60,

табл. 5.61).

Таблица 5.60

Х1Х2 Хз<ршт

XtXsX6

1 2

4 7

0 ' = 0 • <Ршт 1

о" = о.^шт

0 0