Гонтарь И.Н., Волчихина Н.И. Сопротивление материалов
Подождите немного. Документ загружается.

181
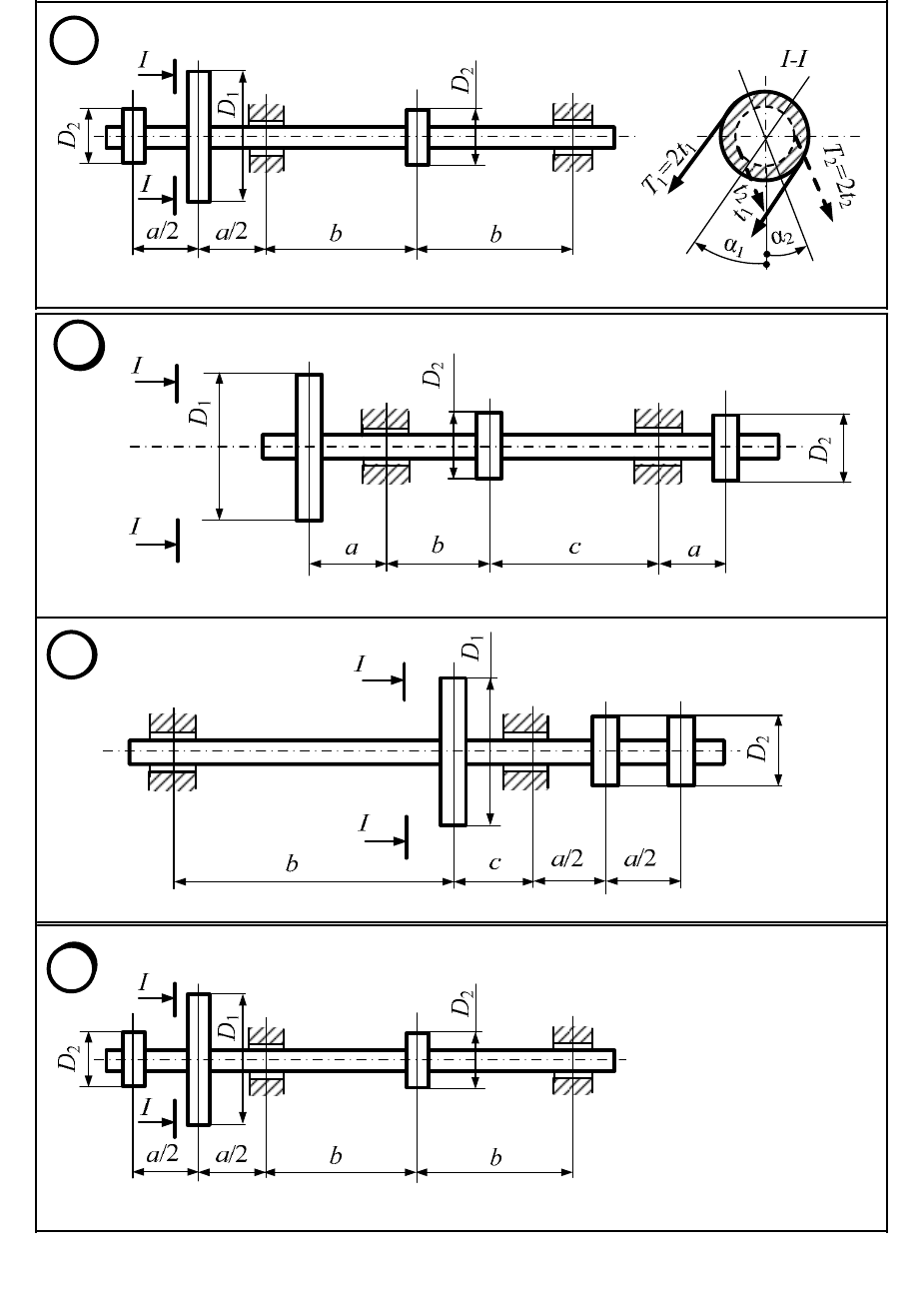
Рисунок 6.1.1 (продолжение)
21
22
23
24
182
D
1
D
2
D
2
T
1
=
2
t
1
T
2
=
2
t
2
t
1
t
2
D
2
D
1
D
2
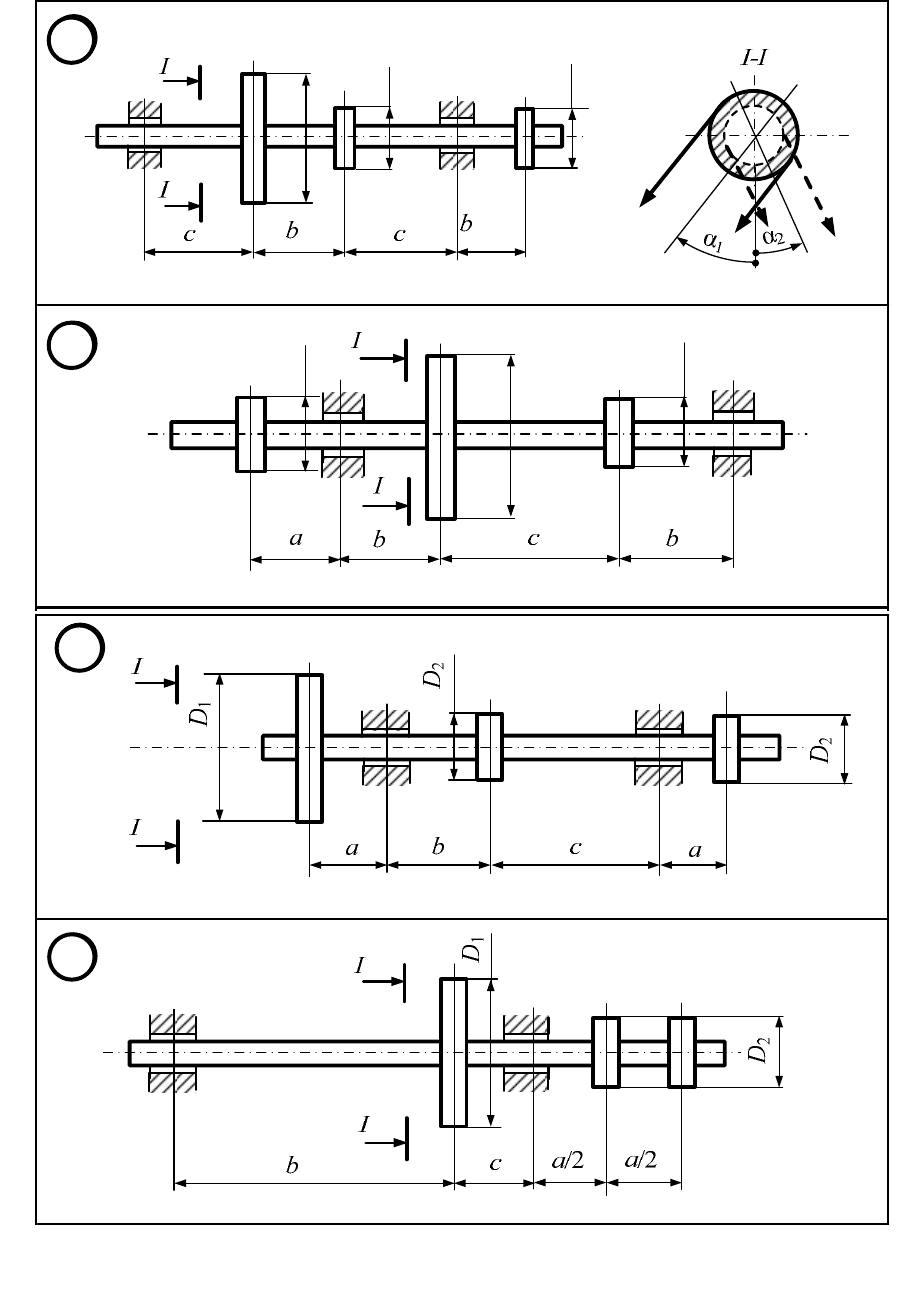
Рисунок 6.1.1 (продолжение)
25
26
27
28
183
D
1
D
2
D
2
T
1
=2t
1
T
2
=2
t
2
t
1
t
2
α
2
D
2
D
1
D
2
D
1
D
2
D
2
D
1
D
2
D
2
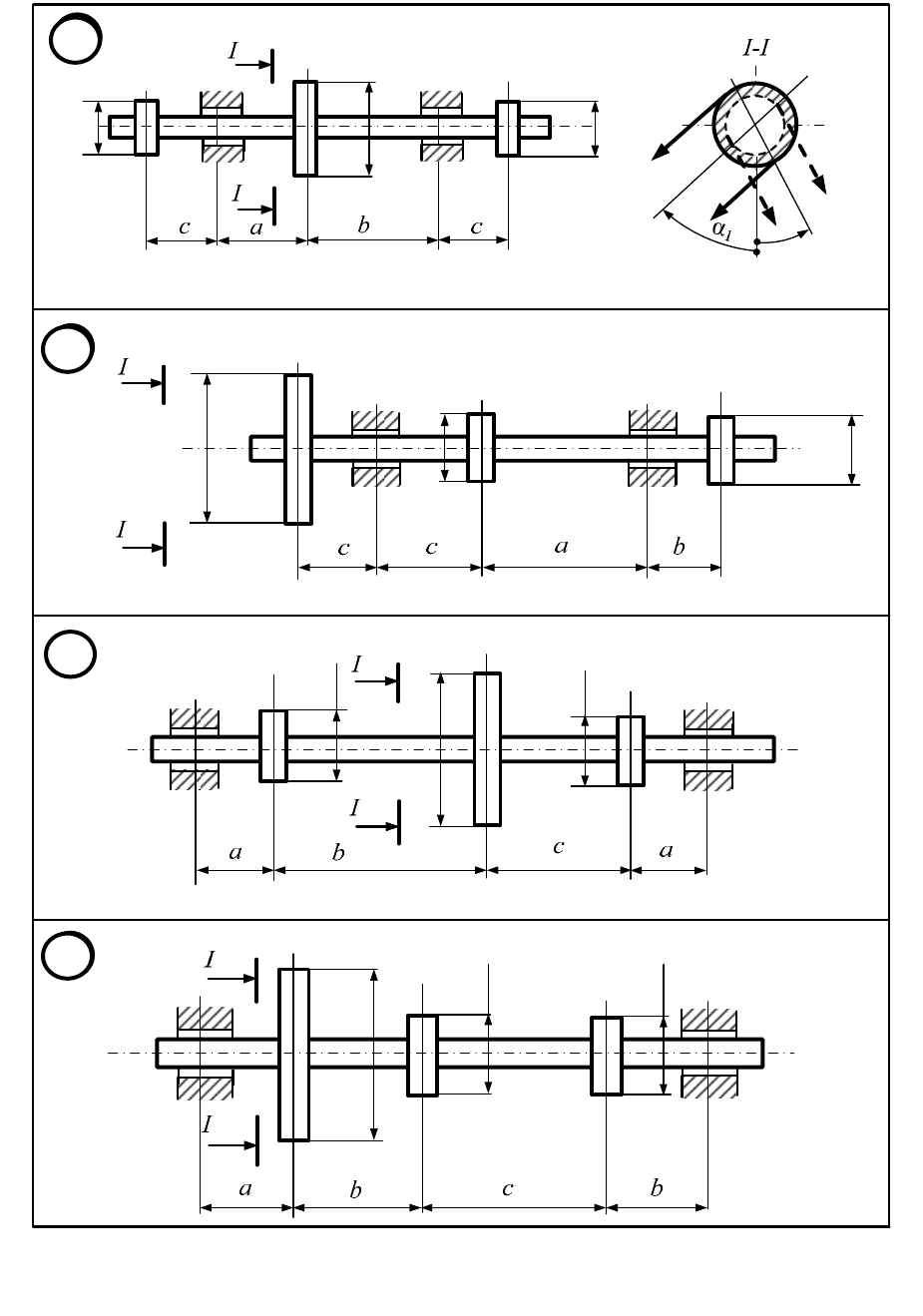
Рисунок 6.1.1 (продолжение)
29
30
31
32

184
Пример выполнения
Расчёт на прочность вала круглого поперечного сечения
при кручении с изгибом
Вал ремённой передачи несёт на себе три шкива, один из которых яв-
ляется ведущим, а два других − ведомыми. Ведущий шкив с помощью ре-
мённой передачи соединён с электродвигателем. От ведомых шкивов ремни
идут к станкам. Ветви ремней у каждого шкива параллельны друг другу и
наклонены к горизонтали под углами
α
1
и α
2
. Усилие в сбегающей ветви
ремня, идущей к электродвигателю ведомого шкива, вдвое больше, чем
в набегающей. В набегающих ветвях ведомых шкивов, идущих к станкам,
усилие вдвое больше, чем в сбегающих. Ведущий шкив передаёт мощ-
ность N
1
(кВт); частота вращения вала − n (об ⋅ мин
−1
).
Цель:
− рассчитать по эпюрам крутящего момента и результирующего из-
гибающего момента наибольший эквивалентный момент вала по четвёртой
теории прочности;
−
подобрать необходимые размеры круглого и кольцевого попереч-
ных сечений валов;
−
сравнить веса валов сплошного и кольцевого поперечных сечений.
Исходные данные принять по таблице 6.1.1 и рисунку 6.1.1.
В расчётах массу вала и шкивов не учитывать.
Исходные данные по варианту ______ приняты по таблице 6.1.1 и ри-
сунку 6.1.1.
Материал вала – Сталь 40, σ
т
= 340 МПа.
Коэффициент запаса прочности n = 1,6.
Динамические характеристики вала:
мощность ведущего шкива N
1
= 11,0 кВт;
скорость вращения вала n = 120 об · мин
–1
.
Геометрические характеристики вала:
а = 0,4 м; b = 0,3 м; с = 0,18 м;
D
1
= 0,4 м; D
2
= 0,35 м; D
3
= 0,35 м;
α
1
= 0 º; α
2
= 60 º.
Отношение диаметров кольцевого сечения вала
8,0==α
D
d
.
185
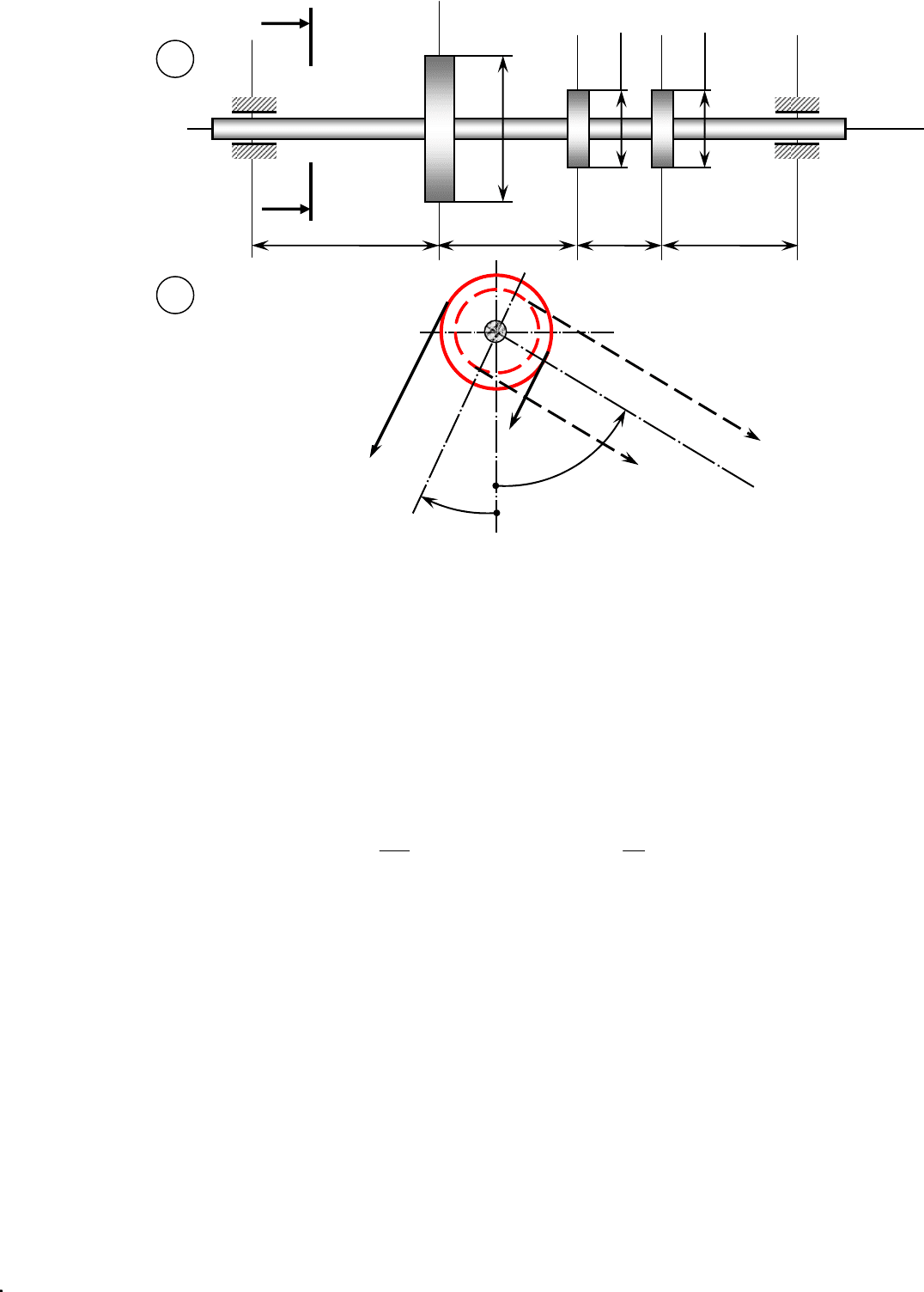
1 Вычерчиваем заданную схему вала (рисунок 6.1.1.1).
2
Определяем мощности на ведомых шкивах.
По условию задачи диаметры ведомых шкивов одинаковы, скорость
вращения n у них тоже одинаковая, поэтому потребляемые мощности тоже
одинаковые N
2
= N
3
.
Сумма потребляемой мощности должна быть равна
мощности на ведущем шкиве:
N
2
+ N
3
= N
1
,
откуда
2
1
32
N
NN == ,
кВт5,5
2
11
32
=== NN .
Скручивающий момент ведущего шкива уравновешивается момента-
ми на ведомых шкивах. Вращение на ведомых шкивах происходит в проти-
воположную сторону относительно вращения ведущего шкива (рису-
нок 6.1.1.1,б, вид I-I). Так как по условию задачи диаметры ведомых шкивов
и мощности одинаковые, то моменты М
2
и М
3
имеют равные значения М.
3
Вычерчиваем расчётную схему вала (рисунок 6.1.1.2).
а − схема расположения шкивов; б – вид I-I : схема усилий на шкивах 2 и 3
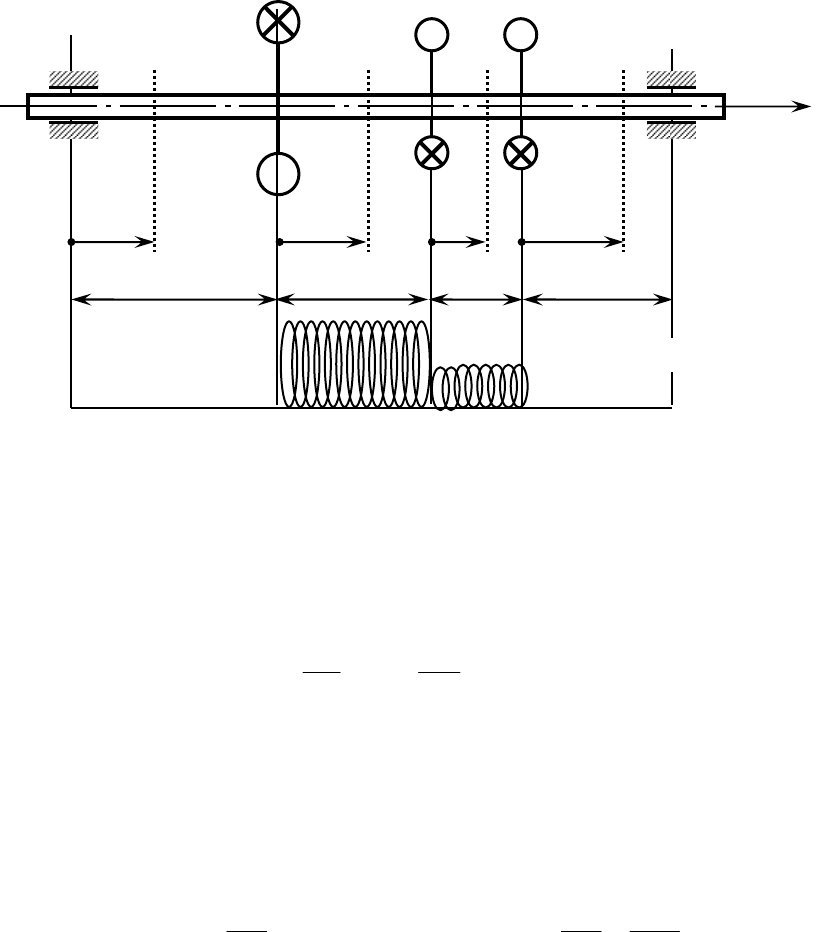
Рисунок 6.1.1.1 − Заданная схема вала
a b
c
b
1шкив 2 шкив 3 шкив
I
I
D
2
D
1
D
3
а
t
2
=
t
3
α
2
t
1
Т
1
= 2
t
1
α
1
Т
2
= Т
3
= 2
t
2
Вид по I-I
б
б
186
Определяем внешние скручивающие моменты, действующие на вал, и
крутящие моменты. Внешний скручивающий момент M
1
на ведущем шкиве
по заданной мощности N
1
и скорости вращения вала n равен
мкН88,0
120
11
55,955,9
1
1
⋅===
n
N
M .
Составляем уравнение равновесия для определения числового значе-
ния скручивающих моментов на ведомых шкивах 2 и 3.
За положительное направление внешнего момента принимаем его
вращение против часовой стрелки вдоль оси Z вала со стороны опоры
А:
Σ
mom Z
= 0; М
1
− М
2
− М
3
= 0 ⇒ М
1
= (М
2
+ М
3
) = 2М,
откуда
2
1
32
М
МММ ===
, т. е. имеем м кН44,0
2
88,0
2
1
22
⋅====
М
ММ .
Внешние моменты определены:
М
1
= 0,88 кН ⋅ м,
М
2
= 0,44 кН ⋅ м,
М
3
= 0,44 кН ⋅ м.
4 Определяем крутящие моменты на каждом участке, используя ме-
тод сечений. Разбиваем вал на участки (см. рисунок 6.1.1.2).
I участок
A – B. На участке от границы A до B моментов нет.
М
к
I
= 0.
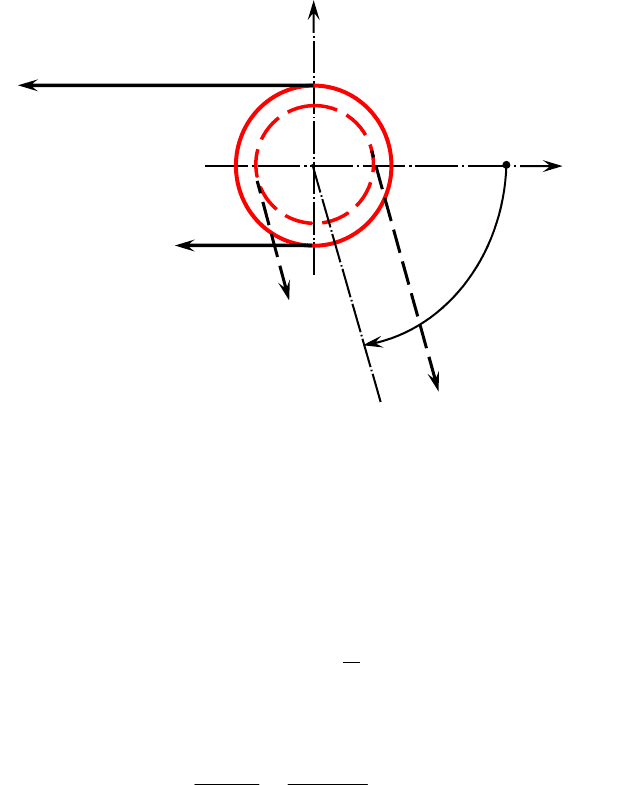
Рисунок 6.1.1.2 − Расчётная схема вала для определения внешних
М
1
, М
2
, М
3
и крутящих моментов. Эпюра крутящих моментов
0 0
0,88
0,44
Эпюра М
к
Z
М
1
М
2
М
3
●●
●
а b
c
b
Z
1
Z
2
Z
3
Z
4
А В
С
D
E
I II
III
IV
187
II участок
B – C. М
к
II
= М
1
= 0,88 кН ⋅ м (const); в любом сечении
II участка крутящий момент имеет значение 0,88 кН ⋅ м.
III участок
С – D. М
к
III
= М
1
– М
2
=0,88 – 0,44 = 0,44 кН ⋅ м
(const).
IV участок
D – E. М
к
IV
= М
1
– М
2
– М
3
= 0,88 – 0,44 – 0,44 = 0.
Крутящие моменты определены. Строим эпюру крутящих момен-
тов М
к
(см. рисунок 6.1.1.2).
5 Для определения изгибающих моментов вычерчиваем расчётную
схему усилий на шкивах 1, 2 и 3 (рисунок 6.1.1.3), которые вызывают изгиб
оси вала.
Определяем окружные усилия t
i
, действующие на шкивы.
Выражаем найденные скручивающие моменты на шкивах через кру-
тящие моменты и окружные усилия.
Ведущий шкив:
11
II
к1
2
1
tDMM ==
.
Усилие натяжения набегающей ветви
кН4,4
4,0
88,02
2
1
II
к
1
=
⋅
==
D
M
t .
Натяжение сбегающей ветви Т
1
= 2t
1
= 2 · 4,4 = 8,8 кН.
6 Определяем давления R
i
шкивов на вал и составляющие давления
R
iх
, R
iy
от каждого шкива, изгибающие вал в горизонтальной и вертикальной
плоскостях.
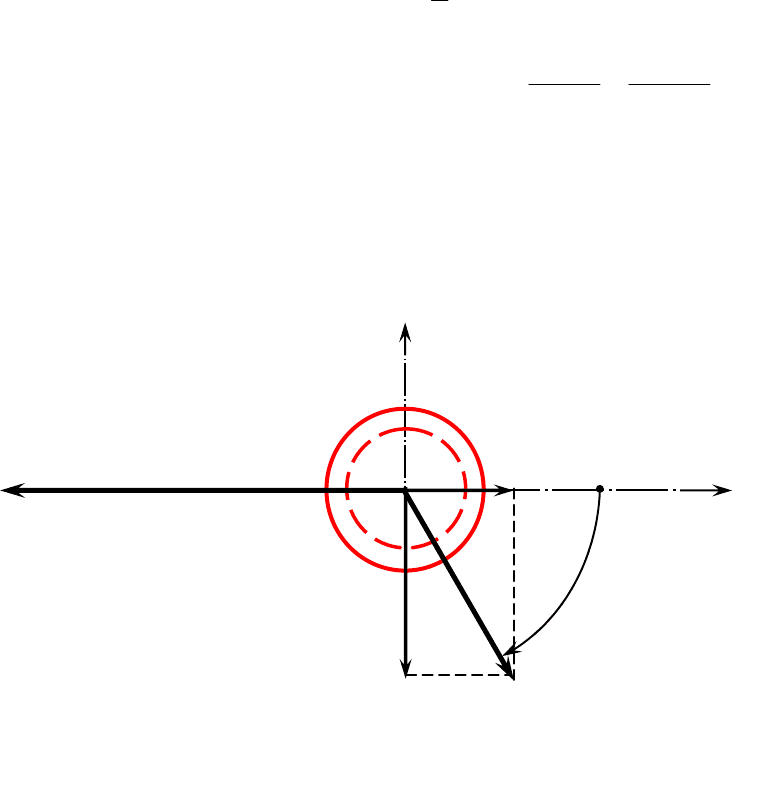
Рисунок 6.1.1.3 − Схема усилий на шкивах 1, 2 и 3
t
2
= t
3
α
2
t
1
Т
1
= 2
t
1
Т
2
= Т
3
= 2t
2
Х
Y
α
1
=0
O
188
Равнодействующая окружных усилий на ведущем шкиве
R
1
= t
1
+Т
1
= 3 t
1
= 3 · 4,4 = 13,2 кН, R
1
= 13,2 кН.
Ведомые шкивы
22
III
к32
2
1
tDMMM ===
;
откуда при условии, что t
2
= t
3
,
имеем кН5,2
35,0
44,02
2
2
III
к
32
=
⋅
===
D
M
tt .
Равнодействующая окружных усилий на ведомых шкивах
R
2
= R
3
= t
2
+Т
2
= 3 t
2
= 3 · 2,5 = 7,5 кН. R
2
= R
3
= 7,5 кН.
В сечениях, где посажены шкивы, вал нагружен горизонтальной си-
лой R
1
и наклонными силами R
2
, R
3
(рисунок 6.1.1.4).
Для простоты вычисления наибольшего изгибающего момента опре-
деляем отдельно изгибающие моменты в вертикальной и отдельно в гори-
зонтальной плоскости, а затем просуммируем их геометрически.
Для этого разложим наклонные силы по координатным осям – на го-
ризонтальные и вертикальные составляющие (см. рисунок 6.1.1.4).
7 Составляем схему нагружения вала в вертикальной плоскости YOZ.
Внешние
вертикальные силы – активные и реактивные: R
2Y
, R
3Y
, R
ВY
, R
АY
.
Составляем расчётную схему вала при действии вертикальных сил
(рисунок 6.1.1.5).
O
Рисунок 6.1.1.4 − Схема сил, изгибающих вал,
приложенных к шкивам
α
2
R
1
R
2
= R
3
Х
Y
R
2
х
= R
3
х
R
2Y
= R
3Y
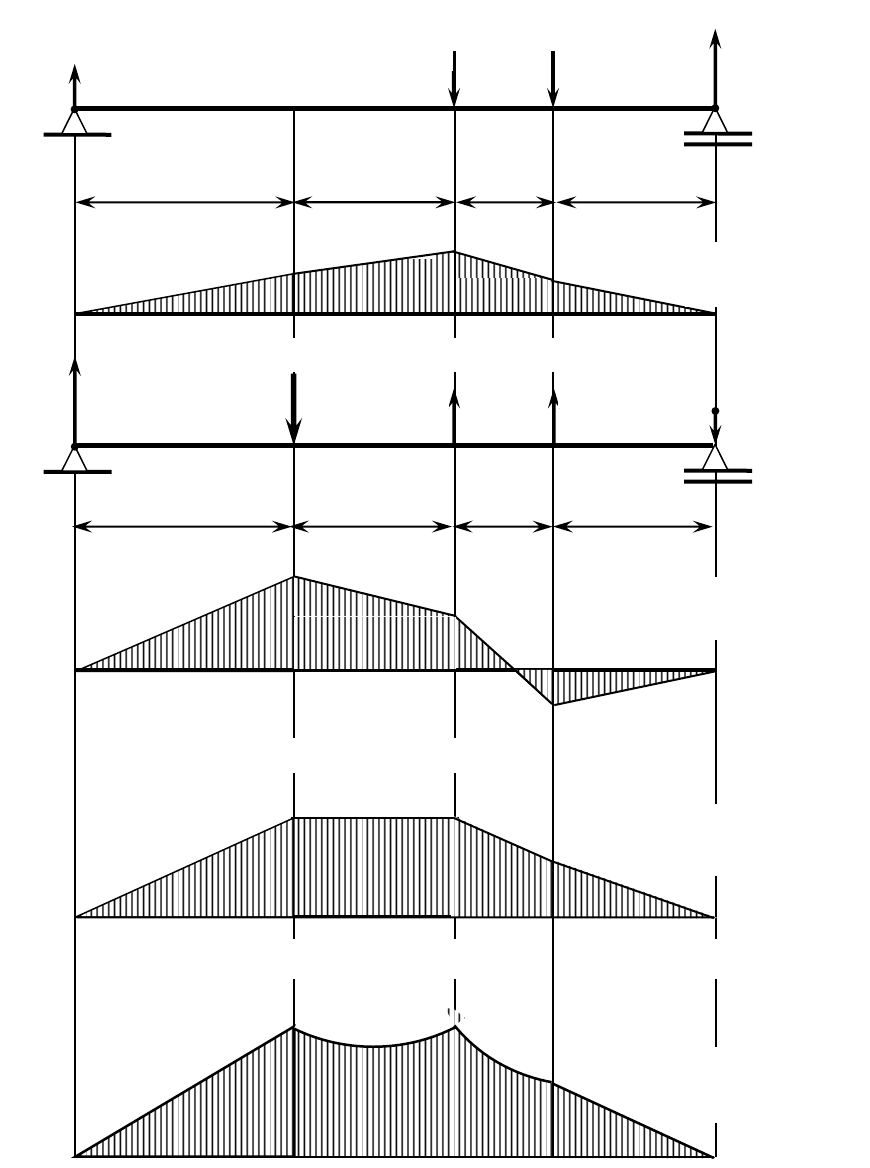
189
Рисунок 6.1.1.5 − Расчётные схемы вала
и эпюры
М
в
, М
г
, М
и
, М
экв
Вертикальная плоскость
R
YA
B
E
D
C
A
R
2Y
R
3Y
R
B
Y
a b
c
b
2
,
6
1,72
3,01
Эпюра М
в
,
кН·м
0 0
Эпюра М
экв
,
кН·м
3,13
2,64
3,13
Результирующая эпюра эквивалентных моментов М
экв
0 0
Результирующий изгибающий момент
Эпюра М
и
,
кН·м
3,04 3,04
2,61
0 0
2
,
5
0,42
0,16
Эпюр
а
М
г
,
кН·м
0 0
Горизонтальная плоскость
R
A
Х
B
E
D
C
A
R
2
Х
R
3
Х
R
B
Х
R
1
Х
a b
c
b
190
Давление шкивов в вертикальной плоскости определяем проецирова-
нием их на ось Y:
R
1Y
= 0, так как α
1
= 0.
R
2Y
= R
2
· sin α
2
= 7,5 · sin 60 º = 6,5 кН ⋅ м; R
2Y
= R
3Y
= 6,5 кН ⋅ м.
Реакции опор определяем из условий равновесия всех внешних вер-
тикальных сил:
∑mom
A = 0; R
ВY
·L – R
2Y
(а + b) – R
3Y
(a + b + c) = 0,
где L – длина вала; L = a + b + c + b = 0,4 + 0,3 + 0,18 + 0,3 = 1,18 м.
R
ВY
·1,18 – 6,5(0,4 + 0,3) – 6,5(0,4 + 0,3 + 0,18) = 0,
откуда R
ВY
= 8,7 кН.
∑mom
В = 0; – R
АY
·L + R
2Y
(b + с +b) + R
3Y
b = 0,
– R
АY
·1,18 + 6,5(0,18 + 0,3) + 6,5 · 0,3 = 0,
откуда R
АY
= 4,3 кН.
Проверка вычислений. ΣY = 0; R
АY
– R
2Y
– R
3Y
+ R
ВY
= 0;
4,3 – 6,5– 6,5 + 8,7 = 0. Силы уравновешены.
Вычисления выполнены верно.
Определяем изгибающие моменты в вертикальной плоскости, пользу-
ясь методом сечений на каждом участке вала:
I участок
A – B. М
В
I
= R
АY
· z
1
; 0 ≤ z
1
≤ a = 0,4 м;
z
1
= 0 М
В
I
= 0;
z
1
= a = 0,4 м, М
В
I
= 4,3 · 0,4 = 1,72 кН ⋅ м;
II участок
B – C. М
В
II
= R
А
(а + z
2
); 0 ≤ z
2
≤ b = 0,3 м;
z
2
= 0 М
В
II
= 4,3 · 0,4 = 1,72 кН ⋅ м;
z
2
= b = 0,3 м; М
В
II
= 4,3 (0,4 + 0,3) = 3,01 кН ⋅ м;
III участок
С – D. М
В
III
= R
АY
(а + b + z
3
) – R
2Y
· z
3
; 0 ≤ z
3
≤ c = 0,118 м;
z
3
= 0 М
В
III
= 4,3 (0,4 + 0,3) = 3,01 кН ⋅ м;
z
3
= c = 0,18 м, М
В
III
= 4,3 (0,4 + 0,3 + 0,18) – 6,5 ⋅ 0,18 = 2,61 кН ⋅ м;
IV участок
D – E.
М
В
IV
= R
АY
(а + b + с + z
4
) – R
2Y
(с + z
4
) – R
3Y
· z
4
; 0 ≤ z
4
≤ b = 0,3 м;
Z
4
= 0 М
В
IV
= 4,3 (0,4 + 0,3 + 0,18) – 6,5 · 0,18 = 2,61 кН ⋅ м;
z
4
= b = 0,3 м,
М
В
IV
= 4,3 (0,4 + 0,3 + 0,18 + 0,3) – 6,5(0,18 + 0,3) – 6,5 · 0,3 = 0,004 кН ⋅ м.
По условиям закрепления в опоре В не должно возникать изги-
бающих моментов
. Расчётом это подтверждается.
