Gockenbach M.S. Partial Differential Equations. Analytical and Numerical Methods
Подождите немного. Документ загружается.

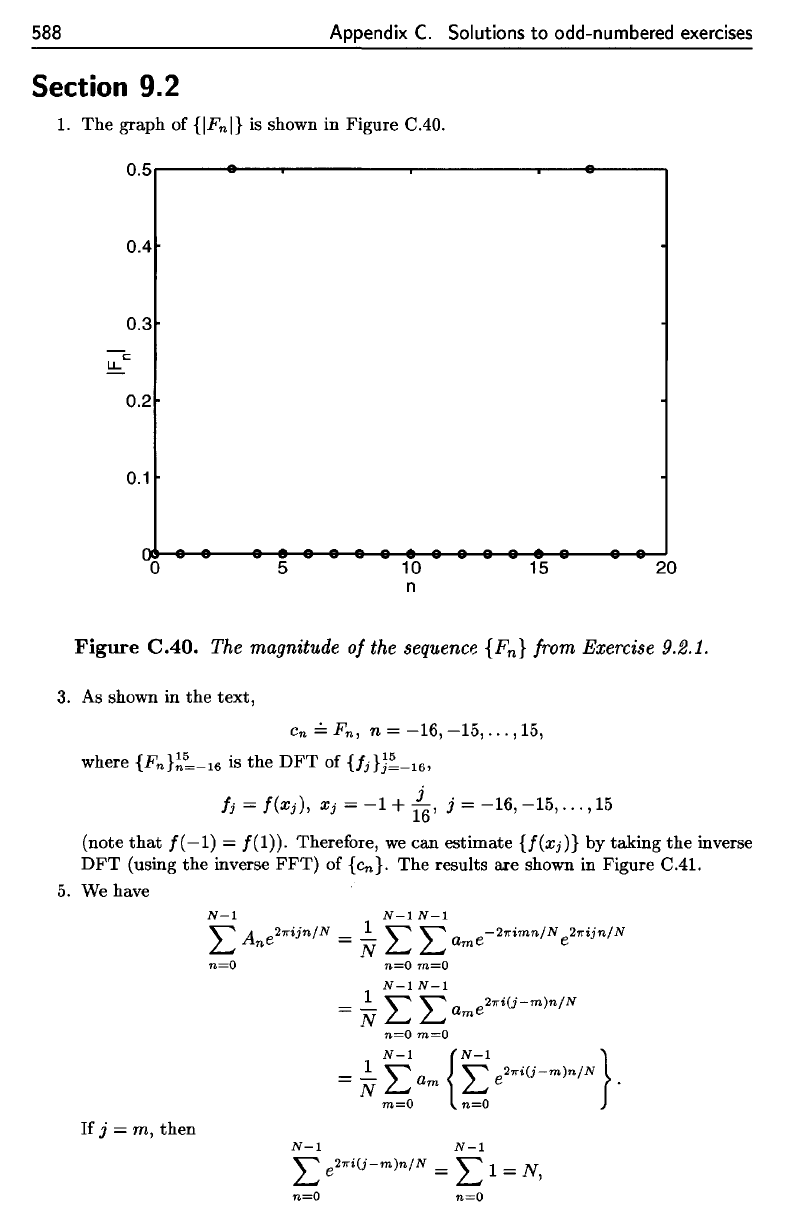
588
Appendix
C.
Solutions
to
odd-numbered
exercises
Section
9.2
1.
The
graph
of
{|F
n
|}
is
shown
in
Figure
C.40.
Figure
C.40.
The
magnitude
of
the
sequence
{F
n
}
from Exercise
9.2.1.
3.
As
shown
in the
text,
where
{F
n
}*
5
=
_
16
is the DFT of
{/j}jl_
16
,
(note
that
/(—I)
=
/(!))•
Therefore,
we can
estimate
{f(xj}}
by
taking
the
inverse
DFT
(using
the
inverse
FFT)
of
{c
n
}.
The
results
are
shown
in
Figure
C.41.
5.
We
have
If j — ra,
then
588
Appendix
C.
Solutions
to
odd-numbered exercises
Section 9.2
1.
The
graph
of {IFnI} is shown in Figure
C.4D.
0.5.------......------r-------r--
......
--
.......
0.4
0.3
c::
LL
0.2
0.1
~O
5
10
n
15 20
Figure
C.40.
The magnitude
of
the sequence {Fn} from Exercise 9.2.1.
3. As shown in
the
text,
en
==
Fn,
n =
-16, -15,
...
,15,
where
{Fn}~~-16
is
the
DFT
of
{Ii
}J~-16'
fj
=
f(xj),
Xj
=
-1
+
:6'
j =
-16, -15,
...
,15
(note
that
f(
-1)
=
f(l)).
Therefore,
we
can estimate
{f(Xj)}
by
taking
the
inverse
DFT
(using
the
inverse
FFT)
of {en}.
The
results are shown in Figure C.41.
5.
We have
If
j =
m,
then
N-l N-l
N-l
"A
e2rrijn/N
_
..!.
" "
-2rrimn/N
2rrijn/N
~
n - N
~
~ame
e
n=O n=O m=O
N-l
N-l
_ 1
""
2rri(j-m)n/N
-
N~~ame
n=O
m=O
N-l
{N-l
}
_
..!.
"
"2rri(j-m)n/N
-
N~am
~e
.
m=O
n=O
N-l N-l
L e
2rri
(j-m)n/N
=
2:
1 =
N,
n=O
n=O
Appendix
C.
Solutions
to
odd-numbered
exercises
589
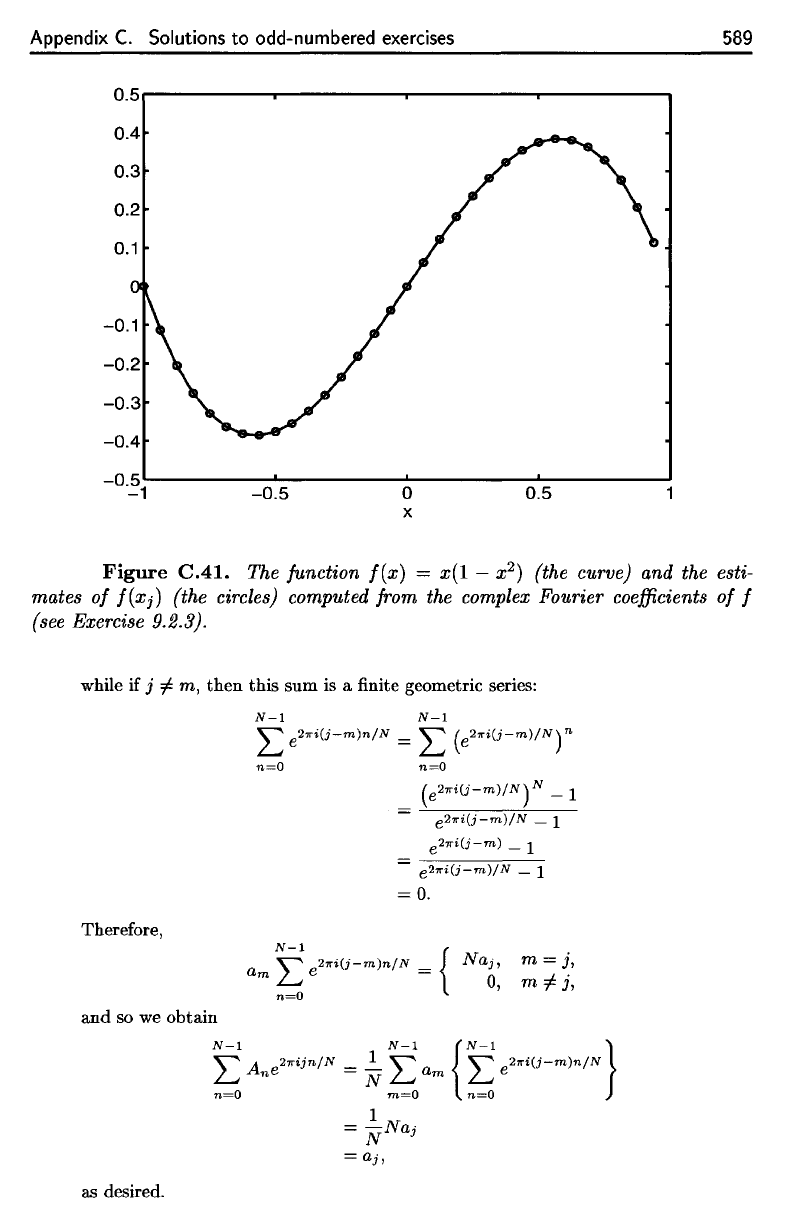
Figure C.41.
The
function
f(x)
=
x(l — x
2
)
(the
curve)
and the
esti-
mates
of
f(xj)
(the
circles) computed from
the
complex Fourier
coefficients
of f
(see
Exercise 9.2.3).
while
if j
^
m,
then this
sum is a finite
geometric series:
Therefore,
and so we
obtain
as
desired.
Appendix
C.
Solutions
to
odd-numbered exercises
0.5.....-----~----"""T""----~-------.
-0.5~----~----~~----~----~
-1
-0.5
o
x
0.5
589
Figure
C.4l.
The function
f(x)
=
x(l
- x
2
)
(the curve) and the esti-
mates
of
f(xj)
(the circles) computed from the complex Fourier coefficients
of
f
(see Exercise 9.2.3).
while if j
=/=
m,
then
this sum is a finite geometric series:
Therefore,
N-l N-l
L e
21ri
(j-m)n/N
= L
(e
2rri
(j-m)/N)n
n=O n=O
(e
2
1l"iu-m)/N)N
_ 1
e
2
1l"i(j-m)/N
- 1
e
27Ti
(j-m)
- 1
e
2rri
(j-m)/N
- 1
=0.
N-l
{
~
2rri(j-m)n/N_
am
L.J e -
n=O
m=j,
m
=/=j,
and
so
we
obtain
as desired.
N-l
N-l
{N-l
}
~
A
21rijn/N
_
..!.
~ ~
27Ti(j-m)n/N
L.J n
e
- N L.J am L.J e
n=O
m=O
n=O
1
=
-Naj
N
=
aj,

590
Appendix
C.
Solutions
to
odd-numbered
exercises
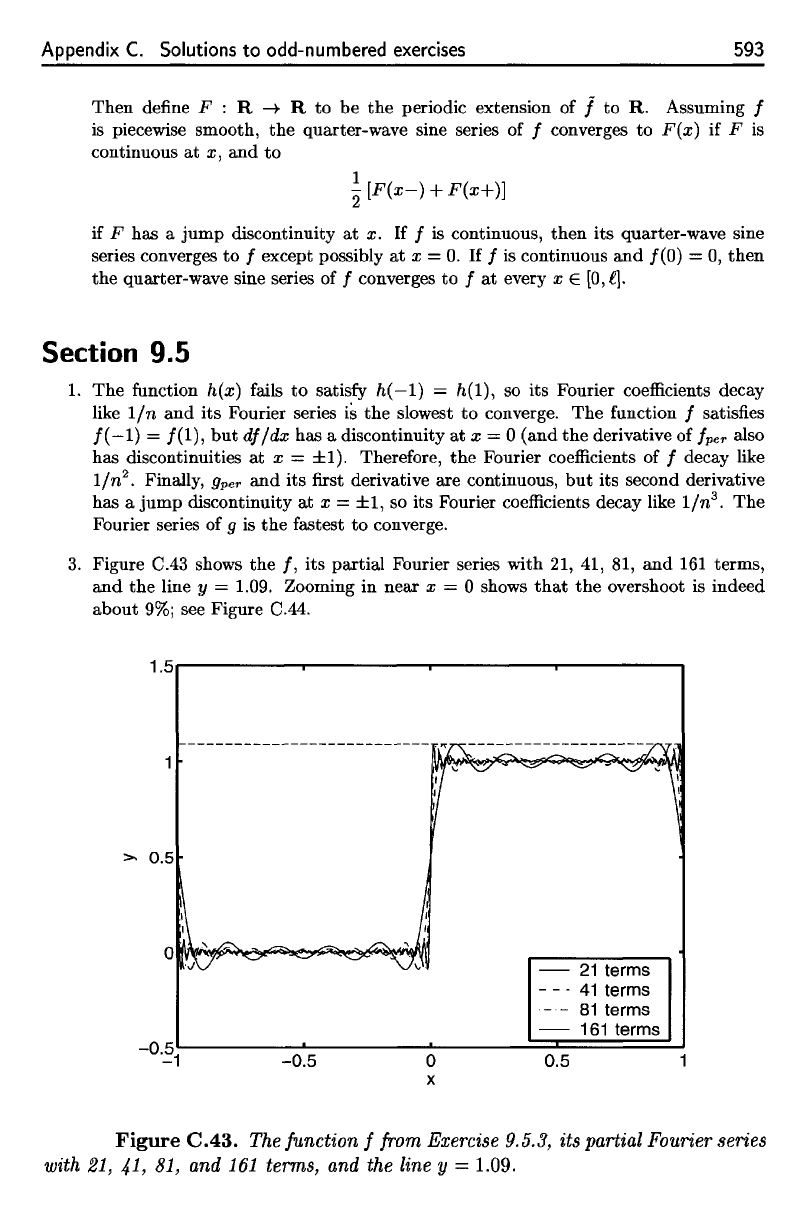
7.
Below
we
show
the
exact Fourier sine
coefficients
of /, the
coefficients
estimated
by
the
DST,
and the
relative error. Since both
a
n
and the
estimated
a
n
are
zero
for
n
even,
we
show only
a
n
for n
odd.
9.
We
have
By
the
hint,
is
either
N/2 or 0,
depending
on
whether
ra = j or
not.
It
then
follows
immediately
that
which
is
what
we
wanted
to
prove.
Section
9.3
1. The
partial Fourier sine series, with
50
terms,
is
shown
in
Figure
C.42.
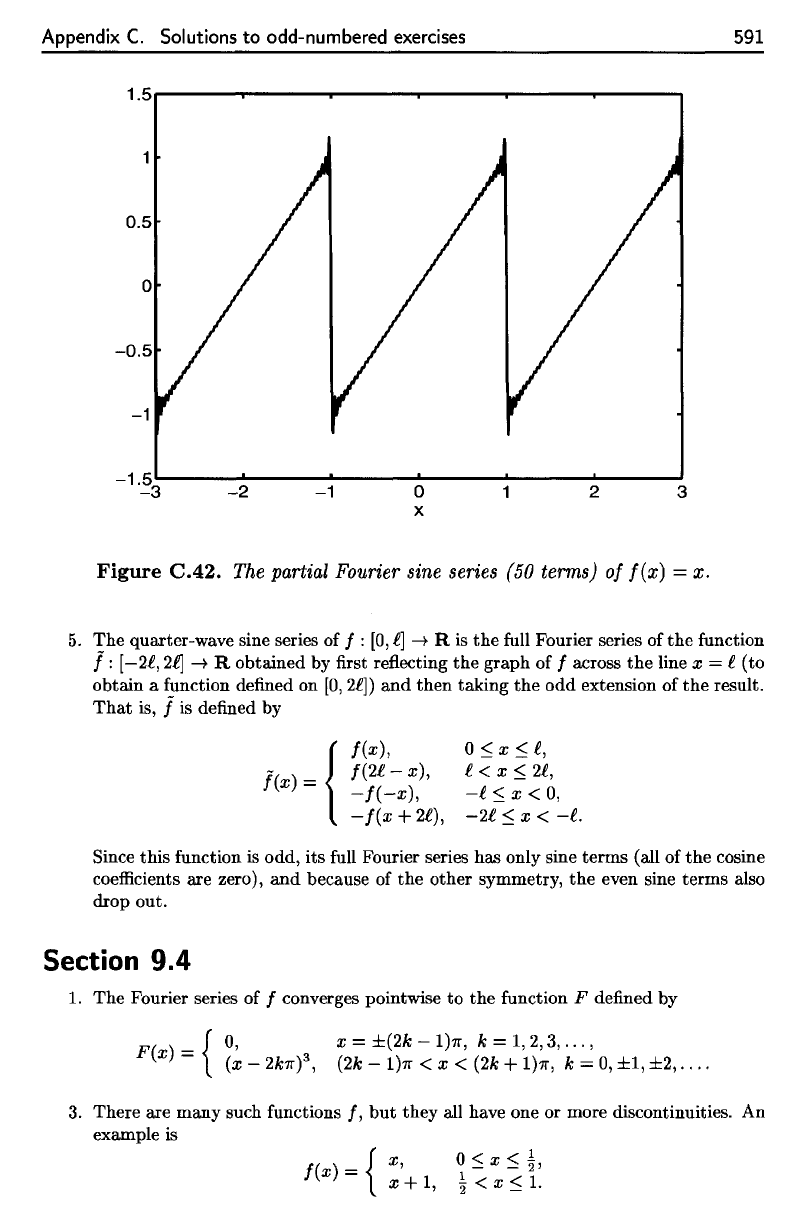
It
appears
that
the
series converges
to the
function
F
satisfying
The
period
of
this
function
is 2.
3. (a) The odd
extension
f
0
dd
is
continuous
on
[—I,
t]
only
if
/(O)
= 0.
Otherwise
fodd
has a
jump
discontinuity
at x = 0.
(b)
The
even extension
f
even
is
continuous
on
[—•£,•£]
for
every continuous
/
[0,
f\
-»-
R.
590
Appendix
C.
Solutions
to
odd-numbered exercises
7.
Below we show
the
exact Fourier sine coefficients
of
I,
the
coefficients
estimated
by
the
DST,
and
the
relative error. Since
both
an
and
the
estimated
an
are
zero for n
even,
we
show only
an
for n odd.
n
an
estimated
an
relative error
1
2.5801.10-
1
2.5801
.10-
1
6.2121 .
10-
6
3
9.5560 .
10-
3
9.5511 .
10-
3
5.1571 .
10-
4
5
2.0641 .
10-
3
2.0555 .
10-
3
4.1824 .
10-
3
7
7.5222 .
10-
4
7.3918 .
10-
4
1.7340 .
10-
2
9
3.5393 .
10-
4
3.3531 .
10-
4
5.2608 .
10-
2
11
1.9385 .
10-
4
1.6778 .
10-
4
1.3448.10-
1
13
1.1744.10-
4
8.0874.10-
5
3.1135.10-
1
15
7.6448 .
10-
5
2.4279 .
10-
5
6.8241.10-
1
9.
We have
N-1 N-1 N-1
2
" F .
(imr)
4""
f .
(mn7r)
.
(in7r)
~
n
sm
N =
~~
m
sm
-;;;-
sm
N
n=l n=l
m=l
N-1 N-1
= 4
Lim
L sin
(m;7r)
sin
e~7r).
m=l
n=l
By
the
hint,
~
.
(mn7r)
.
(in7r)
~
sm
-;;;-
sm
N
n=l
is
either
N
/2
or
0,
depending
on
whether
m = i or not.
It
then
follows immediately
that
~
.
(in7r)
N
2
~
Fn
sm
N =
4"2fJ
=
2NfJ,
n=l
which is
what
we
wanted
to
prove.
Section 9.3
1.
The
partial
Fourier sine series,
with
50
terms, is shown
in
Figure C.42.
It
appears
that
the
series converges
to
the
function F satisfying
F(x)
= x - 2k,
-2k
- 1 < x <
2k
+
1,
k =
0,
±1, ±2,
....
The
period
of
this
function is
2.
3. (a)
The
odd
extension
IOdd
is continuous on [-£,
£]
only
if
I(a) =
a.
Otherwise,
IOdd
has a
jump
discontinuity
at
x =
o.
(b)
The
even extension
lev
en
is continuous on [-£,
£]
for every continuous I :
[a,£]
-t
R.
Appendix
C.
Solutions
to
odd-numbered
exercises
591
5.
The
quarter-wave
sine series
of / : [0, i]
—>•
R is the
full
Fourier series
of the
function
/ :
[—2i,
2i]
-»
R
obtained
by first
reflecting
the
graph
of /
across
the
line
x = t (to
obtain
a
function
defined
on [0,
21])
and
then taking
the odd
extension
of the
result.
That
is,
/is
defined
by
Since
this
function
is
odd,
its
full
Fourier
series
has
only sine
terms
(all
of the
cosine
coefficients
are
zero),
and
because
of the
other symmetry,
the
even sine terms also
drop out.
Section
9.4
1.
The
Fourier series
of /
converges
pointwise
to the
function
F
defined
by
3.
There
are
many such
functions
/, but
they
all
have
one or
more discontinuities.
An
Figure
C.42.
The
partial
Fourier
sine
series
(50
terms)
of
f(x)
= x.
Appendix
C.
Solutions
to
odd-numbered exercises
591
1.5r-----.----....-----.----....----
.........
-----,
1
-1.5~---~------~------~----~-----~----~
-3
-2
-1
0 2 3
x
Figure
C.42.
The partial Fourier sine series (50 terms)
of
f(x)
=
x.
5.
The
quarter-wave sine series of f :
[0,
f]
-+
R is
the
full Fourier series of
the
function
1:
[-2£,2f]
-+
R obtained by first reflecting
the
graph of f across
the
line x = £ (to
obtain a function defined on
[0,
2£])
and
then
taking
the
odd
extension of
the
result.
That
is, 1 is defined by
{
f(x),
f(x)
= f(2£ -
x),
-f(-x),
-f(x
+
2£),
°
:-:::
x:-:::
£,
f<
x:-:::
2£,
-£:-:::
x <
0,
-2£:-:::
x
<-£.
Since
this
function is odd, its full Fourier series has only sine
terms
(all of
the
cosine
coefficients are zero),
and
because of
the
other symmetry,
the
even sine terms also
drop out.
Section 9.4
1.
The
Fourier series of f converges pointwise
to
the
function F defined by
x =
±(2k
-
1)71",
k = 1,2,3,
...
,
(2k -
1)71"
< X < (2k +
1)71",
k =
0,
±1, ±2,
....
3.
There are many such functions f,
but
they
all have one or more discontinuities. An
example is
f(x)
= {
x,
x+
1,
0:-:::
x:-:::
~,
~<x:-:::l.

592
Appendix
C.
Solutions
to
odd-numbered
exercises
5.
If
{/N}
converges
uniformly
to / on [a,
6],
then
it
obviously converges pointwise
(after
all,
the
maximum
difference,
over
x
(E
[a, 6],
between
/N(X)
and
f(x)
converges
to
zero,
so
each individual
difference
must converge
to
zero).
To
prove
that
uniform
convergence
implies mean-square convergence,
define
Then
By
hypothesis,
MN
—>
0 as N
—>
oo,
which gives
the
desired result.
7.
Suppose
/ :
[0,^]
—>•
R is
continuous. Then
f
even
,
the
even, periodic extension
of /
to R, is
defined
by
Obviously,
then,
f
ev
en
is
continuous
on
every interval
(2ki,
(Ik
+
1)1)
and
((2k
—
1)1,2k£.),
that
is,
except possibly
at the
points
Ikt
and (2k
—
l)i,
k — 0, ±1, ±2,
1H7_
1
and
Since
f
e
ven(2kf)
=
/(O)
by
definition, this shows
that
f
even
is
continuous
at x =
2n£.
A
similar calculation shows
that
9.
Given
/ :
[0,
f\
-»•
R,
define
/:
[-21,21]
-»
R by
592
Appendix
C.
Solutions
to
odd-numbered exercises
5.
If
{fN}
converges uniformly
to
f on
[a,
b],
then
it
obviously converges pointwise (after
all,
the
maximum difference, over x E
[a,b],
between fN(X)
and
f(x)
converges
to
zero, so each individual difference
must
converge
to
zero). To prove
that
uniform
convergence implies mean-square convergence, define
MN
=
max{lf(x)
-
fN(X)1
:
a:::;
x
:::;
b}.
Then
lb
If(x)
-
fN(X)12
dx
:::;
J
lb
M'j.
dx
=
MNVb-a.
By hypothesis,
MN
--+
0 as N
--+
00,
which gives
the
desired result.
7.
Suppose f :
[0,
£]
--+
R is continuous.
Then
feven,
the
even, periodic extension of f
to
R,
is defined by
{
f(x
- 2k£),
feven(x)
=
f(
-x
+ 2k£),
2k£
:::;
x < (2k +
1)£,
k =
0,
±1, ±2,
...
,
(2k -
1)£
:::;
x <
2k£,
k = 0, ±1, ±2,
...
.
Obviously, then,
feven
is continuous on every interval (2k£, (2k +
1)£)
and
((2k -
1)£,
2k£),
that
is, except possibly
at
the
points 2k£
and
(2k
-1)£,
k =
0,
±1, ±2,
....
We have
lim
feven(x) = lim
f(-x+2k£)
x~2W-
x~2W-
= lim
f(x)
x~o+
=
f(O)
and
lim feven(x} = lim
f(x
- 2k£)
x~2kl+ x~2kl+
= lim
f(x)
x~o+
= f(O).
Since feven(2k£) = f(O) by definition, this shows
that
feven
is continuous
at
x =
2/';,£.
A similar calculation shows
that
lim feven(x) = lim feven(x) = feven((2k -
1)£)
=
feR),
x~(2k-l)l-
x~(2k-l)l+
and
hence
that
feven
is continuous
at
x = (2k - I)£,
9.
Given f :
[0,
£]
--+
R,
define!
: [-2£,2£]
--+
R by
{
f(x),
lex)
= /(2£ - x),
-fe-x),
-f(x
+
2£),
0:::;
x:::;
£,
£ <
x:::;
2£,
-£:::;
x <
0,
-2£:::;
x <
-f.
Appendix
C.
Solutions
to
odd-numbered
exercises
593
Section
9.5
1.
The
function
h(x)
fails
to
satisfy
h(—1)
=
h(l),
so its
Fourier coefficients decay
like
1/n and its
Fourier series
is the
slowest
to
converge.
The
function
/
satisfies
/(—I)
=
/(I),
but
df/dx
has a
discontinuity
at
re
= 0
(and
the
derivative
of
f
pe
r
also
has
discontinuities
at x =
±1). Therefore,
the
Fourier
coefficients
of /
decay like
1/n
2
.
Finally,
g
pe
r
and its first
derivative
are
continuous,
but its
second derivative
has
a
jump discontinuity
at x = ±1, so its
Fourier coefficients decay like
1/n
3
.
The
Fourier
series
of g is the
fastest
to
converge.
3.
Figure
C.43
shows
the /, its
partial Fourier series with
21, 41, 81, and 161
terms,
and the
line
y =
1.09. Zooming
in
near
x = 0
shows
that
the
overshoot
is
indeed
about
9%;
see
Figure
C.44.
Then
define
F
:
R
—>•
R to be the
periodic extension
of / to R.
Assuming
/
is
piecewise smooth,
the
quarter-wave sine series
of /
converges
to
F(x)
if F is
continuous
at
x,
and to
if
F has a
jump discontinuity
at x. If / is
continuous, then
its
quarter-wave sine
series converges
to /
except possibly
at x = 0. If / is
continuous
and
/(O)
= 0,
then
the
quarter-wave
sine
series
of /
converges
to / at
every
x €
[0,
i}.
Figure C.43.
The
function
f
from
Exercise
9.5.3,
its
partial
Fourier
series
with
21,
41,
81, and 161
terms,
and the
line
y =
1.09.
Appendix
C.
Solutions
to
odd-numbered exercises
593
Then
define F : R
--+
R
to
be
the
periodic extension of f
to
R.
Assuming I
is piecewise smooth,
the
quarter-wave sine series of I converges
to
F(x)
if F
is
continuous
at
x,
and
to
1
"2
[F(x-)
+ F(x+)]
if F has a
jump
discontinuity
at
x.
If
I is continuous,
then
its quarter-wave sine
series converges
to
I except possibly
at
x =
O.
If
I is continuous
and
1(0) =
0,
then
the
quarter-wave sine series of f converges
to
f
at
every x E
[0,
.e].
Section 9.5
1.
The
function
hex)
fails
to
satisfy
h(-l)
=
h(l),
so its Fourier coefficients decay
like
l/n
and
its
Fourier series is
the
slowest
to
converge.
The
function I satisfies
f(
-1)
=
f(l),
but
dl/dx
has a discontinuity
at
x = a
(and
the
derivative of
Iper
also
has discontinuities
at
x =
±1).
Therefore,
the
Fourier coefficients of f decay like
1/n2.
Finally,
gper
and
its
first derivative are continuous,
but
its
second derivative
has a
jump
discontinuity
at
x =
±1,
so its Fourier coefficients decay like
1/n
3
.
The
Fourier series of 9 is
the
fastest
to
converge.
3.
Figure C.43 shows
the
I,
its
partial Fourier series with 21, 41, 81,
and
161
terms,
and
the
line y = 1.09. Zooming in near x = a shows
that
the
overshoot is indeed
about
9%;
see Figure C.44.
1.5~--------~---------r--------~--------~
>-
0.5
-0.5
o
x
-
21
terms
-
_.
41
terms
0.5
81
terms
161 terms
Figure
C.43.
The function f from Exercise 9.5.3, its partial Fourier series
with 21, 41, 81, and
161
terms, and the line y = 1.09.

594
Appendix
C.
Solutions
to
odd-numbered
exercises
Figure
C.44.
Zooming
in on the
overshoot
in
Figure
C.43.
Section
9.6
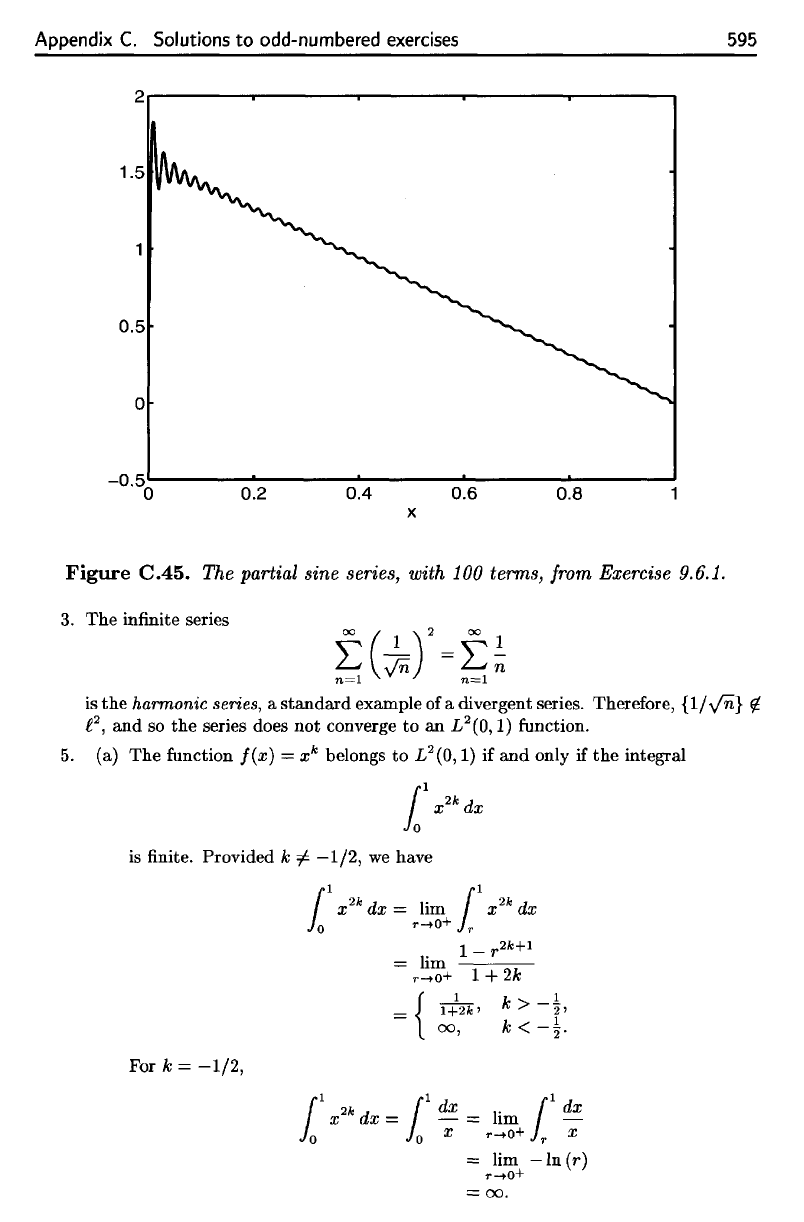
1. (a) The
infinite
series
converges
to a finite
value.
87
Therefore,
{1/n}
G
f
2
and so, by
Theorem 9.36,
the
sine series converges
to a
function
in
L
2
(0,1).
(b)
Figure
C.45
shows
the sum of the first 100
terms
of the
sine series.
The
graph
suggests
that
the
limit
/ is of the
form
f(x)
=
m(l
—
x).
The
Fourier sine
series
of
such
an / are
Therefore,
in
order
that
c
n
=
1/n,
we
must have
m
=
Tr/2.
Therefore,
87
A
standard
result
in the
theory
of
infinite
series
is
that
converges
if
A;
is
greater
than
1.
This
can be
proved,
for
example,
by
comparison
with
the
improper
integral
594
Appendix
C.
Solutions
to
odd-numbered exercises
1.1051--..-----r----...----~====::::c:::===;_,
21
terms
41
terms
1.1
81
terms
161
terms
1.095
>.
1 .09 - - - - - - - - - - - - -
-:-
- - - - - - -
...
- - - - - - - - - - - - -
I,
I \
1.085
1.08
o
ii'
,
I ,
I
i
I i
I
I
i
0.02 0.04
x
,
,
0.06
0.08
Figure
C.44.
Zooming in on the overshoot in Figure C.43.
0.1
Section 9.6
1. (a)
The
infinite series
00
1
Ln
2
n=l
converges
to
a finite value.
87
Therefore,
{lin}
E £2
and
so,
by
Theorem
9.36,
the
sine series converges
to
a function in L2(0, 1).
(b)
Figure
C.45 shows
the
sum
of
the
first 100
terms
of
the
sine series.
The
graph
suggests
that
the
limit
f is
of
the
form
f(x)
=
m(l
- x).
The
Fourier sine
series
of
such
an
f
are
C
n
= 2 t
m(l
- x) sin (mTx) =
2m,
n =
1,2,3,
....
10
n~
Therefore, in
order
that
en =
lin,
we
must
have m =
~/2.
Therefore,
~
f(x)
=
2(1
- x).
87
A standard result in the theory of infinite series
is
that
00
L:k
n=l
converges if k
is
greater than 1. This can be proved, for example,
by
comparison with the improper
integral
f
oo
dx
k'
1 X
Appendix
C.
Solutions
to
odd-numbered
exercises
595
Figure
C.45.
The
partial
sine
series,
with
100
terms,
from Exercise
9.6.1.
3.
The
infinite
series
is
the
harmonic series,
a
standard
example
of a
divergent series. Therefore,
{l/^/n}
0
t
2
,
and so the
series
does
not
converge
to an
L
2
(0,1)
function.
5.
(a) The
function
f(x)
=
x
k
belongs
to
L
2
(0,1)
if and
only
if the
integral
is
finite.
Provided
k
^
—1/2,
we
have
For
A;
=
-1/2,
Appendix
C.
Solutions
to
odd-numbered exercises
595
2.-------~------_,--------T_------_r------_.
-0.5L..--------
.......
---
........
----'----~
o 0.2 0.4 0.6 0.8
x
Figure
C.45.
The partial sine series, with 100 terms, from Exercise 9.6.1.
3.
The
infinite series
00
(
1)2
00
1
~
fo
=~~
is
the
harmonic series, a
standard
example of a divergent series. Therefore, {1/
fo}
(j.
p2,
and
so
the
series does
not
converge
to
an
L2(0,
1) function.
5.
(a)
The
function
f(x)
==
xk belongs
to
L2(0,
1)
if
and
only if
the
integral
is
finite. Provided k
#-
-1/2,
we
have
For
k
==
-1/2,
1
1
X2k
dx
==
lim
11
x
2k
dx
o
r-+O+
r
1 - r
2k
+
1
lim
r-+O+
1 +
2k
=={
1
1+2k'
00,
{1
x
2k
dx
==
t
dx
==
lim
11
dx
10
10
x
r-+O+
r X
==
lim
-In
(r)
r-+O+
==
00.
596
Appendix
C.
Solutions
to
odd-numbered
exercises
Thus
we see
that
/
e
L
2
(0,1)
if and
only
if k >
-1/2.
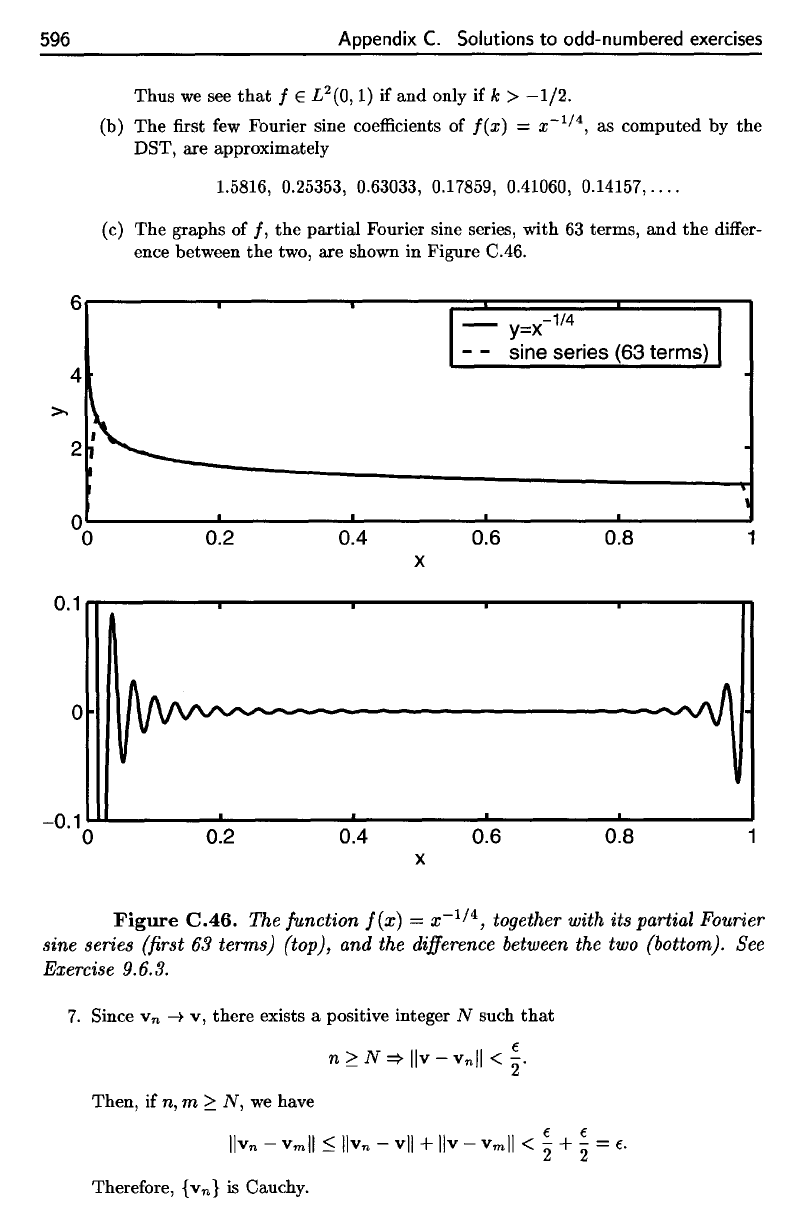
(b)
The first few
Fourier sine
coefficients
of
f(x)
=
a:"
1
/
4
,
as
computed
by the
DST,
are
approximately
1.5816,
0.25353,
0.63033, 0.17859, 0.41060,
0.14157,....
(c)
The
graphs
of /, the
partial Fourier sine series, with
63
terms,
and the
differ-
ence between
the
two,
are
shown
in
Figure
C.46.
Figure
C.46.
The
function
f(x)
= x
1//4
,
together with
its
partial Fourier
sine
series
(first
63
terms)
(top),
and the
difference
between
the two
(bottom).
See
Exercise
9.6.3.
7.
Since
v
n
—>•
v,
there exists
a
positive integer
N
such
that
Then,
if
n,
m
>
TV,
we
have
Therefore,
{v
n
}
is
Cauchy.
596
6
4
2
Appendix
C.
Solutions
to
odd-numbered exercises
Thus
we
see
that
f E L2(0,
1)
if
and
only if k >
-1/2.
(b)
The
first
few
Fourier sine coefficients of
f(x)
=
X-
1
/
4
,
as computed by
the
DST, are approximately
1.5816, 0.25353, 0.63033, 0.17859, 0.41060, 0.14157,
....
(c)
The
graphs of
j,
the
partial Fourier sine series, with
63
terms,
and
the
differ-
ence between
the
two, are shown in Figure C.46.
-
y=x-
1/4
--
sine series (63 terms)
~
•
0.2 0.4 0.6 0.8 1
x
0.1n-------~~------~~------~~-------,---------n
o
-0.1U.------~--------~------~--------~------~
o 0.2 0.4 0.6 0.8 1
x
Figure
C.46.
The function
f(x)
=
X-
1
/
4
,
together with its partial Fourier
sine series (first
63 terms) (top), and the difference between the two (bottom). See
Exercise 9.6.3.
7.
Since
Vn
~
v,
there exists a positive integer N such
that
10
n ? N
~
Ilv
-
vnll
<
2'
Then,
if
n, m ?
N,
we
have
10 10
IIv
n
-
vmll
::;
IIv
n
-
vII
+
IIv
-
vmll
< 2 + 2 =
10.
Therefore,
{v
n
}
is
Cauchy.

Appendix
C.
Solutions
to
odd-numbered
exercises
597
Section
9.7
1. The
proof
is a
direct
calculation, using integration
by
parts
(Green's identity): Sup-
pose
u,
v
£
Cf)(fi).
Then
3.
If t is
very large, then
we can
approximate
-u(x,
t]
by the first
term
in its
gener-
alized
Fourier series. Using
the
same notation
as
before
for the
eigenvalues
and
eigenfunctions
of the
negative Laplacian
on fi, we
have
The
constant
c\
is the first
generalized Fourier
coefficient
of the
initial temperature
5:
The
approximation
is
valid provided
AI
is a
simple
eigenvalue;
that
is,
there
is
only
one
linearly independent eigenvector corresponding
to
AI.
Then
all of the
other
terms
in the
generalized Fourier series decay
to
zero
much more rapidly than does
the first
term.
Section
10.1
1.
We
must
check
that
the
one-point rule gives
the
exact
values
for the
integral
and
when
/(x)
= 1,
/(x)
=
xi,
or
/(x)
=
x<z-
With
/(x)
= 1, we
have
Appendix
C.
Solutions
to
odd-numbered exercises 597
Section 9.7
1.
The
proof is a direct calculation, using integration by
parts
(Green's identity): Sup-
pose
u, v E
eben).
Then
(KDU, v) =
-10
V'.
(k(x)V'u)
v
= 1
k(x)V'u
.
V'v
- {
k(x)v
~u
n
Jon
vn
=
10
k(x)V'u·
V'v
(since v = 0 on
an)
= - r V'.
(k(x)V'v)
u + r
k(x)u
~v
Jn
Jon
vn
=
-10
V'.
(k(x)V'v)
u (since u = 0 on
an)
= (U,KDV).
3.
If
t is very large,
then
we
can approximate
u(x,
t) by
the
first
term
in its gener-
alized Fourier series. Using
the
same notation as before for
the
eigenvalues
and
eigenfunctions of
the
negative Laplacian on
n,
we
have
The
constant C1 is
the
first generalized Fourier coefficient of
the
initial
temperature
5:
In
5'1f;1
C1 =
In'1f;i·
The
approximation is valid provided
>'1
is a simple eigenvalue;
that
is, there is only
one linearly independent eigenvector corresponding
to
>'1.
Then
all
of
the
other
terms in
the
generalized Fourier series decay
to
zero much more rapidly
than
does
the
first term.
Section 10.1
1.
We
must check
that
the
one-point rule gives
the
exact values for
the
integral
when
I(x)
= 1,
I(x)
=
Xl,
or
I(x)
=
X2.
With
I(x)
=
1,
we
have
and
