Gockenbach M.S. Partial Differential Equations. Analytical and Numerical Methods
Подождите немного. Документ загружается.


The
temperature
at the
midpoint
after
20
minutes
is
ti(50,1200)
=
1.58 degrees Celsius.
548
Appendix
C.
Solutions
to
odd-numbered
exercises
and
We
define
and
Then
v
satisfies
7.
Define
v(x,
t) =
u(x,
t)
—
xcos
(t). Then
v
satisfies
the
following
IBVP
(with homo-
geneous
boundary conditions,
but
with
a
nonzero source term):
This IBVP
has
solution
where
The
solution
to the
original IBVP
is
then
u(x,t)
=
v(x,t)
+
xcos(t).
A
graph
of
«(•,
1.0)
is
given
in
Figure
C.ll.
9.
The
temperature
u(x,
t)
satisfies
the
IBVP
The
solution
is
548
and
We define
and
Then
v satisfies
Appendix
C.
Solutions
to
odd-numbered exercises
v(O,
t)
=
u(O,
t)
-
p(O,
t)
= get) - get) =
0,
vel, t) = u(l,
t)
- pel, t) = h(t) - h(t) =
o.
g(x,
t)
=
I(x,
t) -
pc
(~!
(t)
+ 7
(~~
(t) -
~!
(t)) )
x
ifJ(x)
=
1j;(x)
- g(to) -
l(h(to)
- g(to)).
{)v
{)2V
pc
{)t
- K
{)x
2
= g(x,
t),
0 < x <
l,
t > 0,
v(x,to)
=
ifJ(x),
0 < x <
l,
v(O,
t) = 0, t > to,
vel,
t)
=
0,
t > to.
7.
Define vex,
t)
= u(x, t) - x cos (t).
Then
v satisfies
the
following
IBVP
(with homo-
geneous boundary conditions,
but
with a nonzero source term):
{)v
{)2V
.
at
-
{)x2
= x sm (t), 0 < x < 1, t > 0,
v(x,O) = 0, 0 < x < 1,
v(O,
t) =
0,
t >
0,
v(l,t)
=
0,
t >
O.
This
IBVP
has solution
00
v(x,t)
=
Lan(t)
sin (mrx),
n=l
where
(
2(
_l)n
(
()
_n
2
,..2
t
2 2 • ( )
an
t) =
mr
(n
4
7r
4
+ 1) cos t - e - n
7r
sm
t)
.
The
solution
to
the
original
IBVP
is
then
u(x,
t)
= vex, t) + x cos (t). A
graph
of
u(·,1.0) is given in Figure C.11.
9.
The
temperature
u(x, t) satisfies
the
IBVP
{)u
{)2U
pc
at
- K
{)x
2
=
0,
0 < x < 100, t >
0,
u(x,O) =
5,
0 < x < 100,
u(O,
t) = 0, t >
0,
u(100, t) =
0,
t >
O.
The
solution is
00
10(1-(-1)n)
_"n
2
,,2
t
(n7rx)
u(x
t) =
'\:""'"
e
100
2
pc
sin - .
,
~
n7r
100
n=l
The
temperature
at
the
midpoint after
20
minutes is
u(50, 1200)
==
1.58 degrees Celsius.
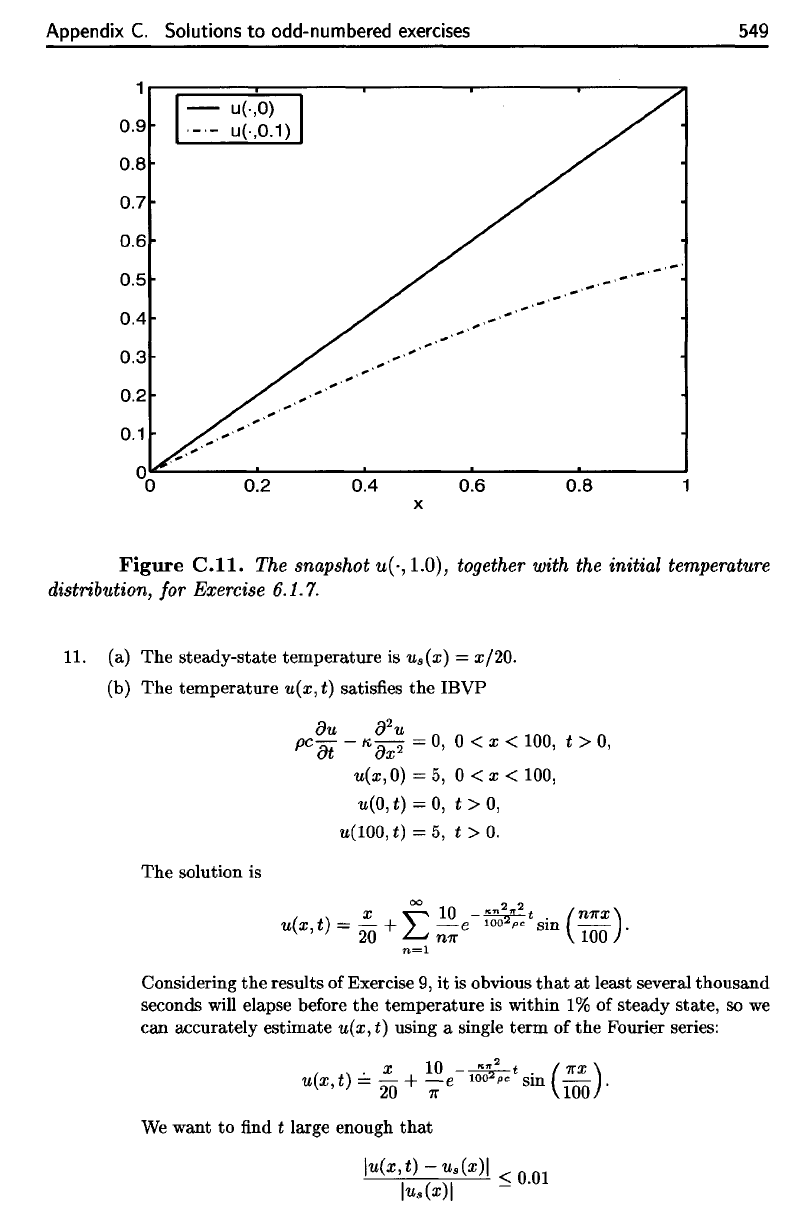
Appendix
C.
Solutions
to
odd-numbered
exercises
549
Figure
C.ll.
The
snapshot
u(-,
1.0),
together with
the
initial temperature
distribution,
for
Exercise
6.1.7.
The
solution
is
Considering
the
results
of
Exercise
9, it is
obvious
that
at
least several thousand
seconds
will
elapse
before
the
temperature
is
within
1% of
steady state,
so we
can
accurately estimate
u(x,t)
using
a
single term
of the
Fourier series:
11. (a) The
steady-state temperature
is
u
s
(x)
=
re/20,
(b)
The
temperature
u(x,t)
satisfies
the
IBVP
We
want
to find t
large enough
that
Appendix
C.
Solutions
to
odd-numbered exercises
549
Figure
C.ll.
The snapshot u(·, 1.0), together with the initial temperature
distribution, for Exercise
6.1.7.
11. (a)
The
steady-state
temperature
is
u.(x)
= x/20.
(b)
The
temperature
u(
x,
t) satisfies
the
IBVP
AU
02U
pc
at
-
K,
ox
2
=
0,
0 < x < 100, t >
0,
u(x,O)
=
5,
0 < x < 100,
u(O,
t) =
0,
t >
0,
u(lOO,
t)
= 5, t >
o.
The
solution is
00
2 2
X L
10
- '''''
"t
(nlrx)
u(x
t) = - +
-e
l002pc
sin
--
.
,
20
nlr
100
n=l
Considering
the
results of Exercise
9,
it
is obvious
that
at
least several
thousand
seconds will elapse before
the
temperature
is
within
1%
of steady state,
so
we
can accurately estimate u(x, t) using a single
term
of
the
Fourier series:
x
10
- ",,2 t (
lrX
)
u(x
t)
==
- +
-e
lO02pc
sin -
,
20
11'
100 .
We want
to
find t large enough
that
lu(x, t) - u.(x)1 < 0.01
lu.(x)1 -

550
Appendix
C.
Solutions
to
odd-numbered
exercises
for
all x
e
[0,100].
Using
our
approximation
for
u,
this
is
equivalent
to
A
graph shows
that
for
all x, so we
need
This yields
About
75
minutes
and 20
seconds
are
required.
Section
6.2
1.
The
solution
is
where
The
graphs
are
given
in
Figure
C.I2.
/
3.
(a)
Ifu,v£
C^[0,4
then
This
shows
that
LN is
symmetric.
550
Appendix
C.
Solutions
to
odd-numbered exercises
for all x E [0,100]. Using
our
approximation for u,
this
is equivalent
to
200
sin (
ffo-
)
7rX
A graph shows
that
200
sin
(;o~)
~2
7rX
for all x, so
we
need
This yields
t >
-100
2
pcln
0.005
~
4520.
- K.7r
2
About
75
minutes
and
20
seconds are required.
Section 6.2
1.
The
solution is
00
u(x,
t) =
do
+ L dne-n21r2t cos (n7rx),
n=1
where
1
1
1
11
2
((-It+
1
-1)
d
o
=
x(1-x)dx=-6'
d
n
=2
x(l-x)cos(n7rx)dx=
22
•
o 0 n 7r
The
graphs are given in Figure C.12. I
3.
(a)
Ifu,v
E C1[0,f],
then
t d
2
(LNU,V)=-
10
dx~(x)v(x)dx
du
Ii
t
du
dv
=-
dx(x)v(x)
0 +
10
dx(x)dx(x)dx
l
i
du
dv .
=
-(x)-(x)dx
(smcedU(O)=du(£)=O)
odx
dx
do;
do;
dv
Ii
t d
2
v
=
u(x)dx(x)
0 -
10
u(x)dx
2
(x)dx
t d
2
= -
10
u(x)
dx~
(x)
dx
(since
~~
(0) =
~~
(£)
= 0)
= (u, LNV).
This shows
that
LN
is symmetric.
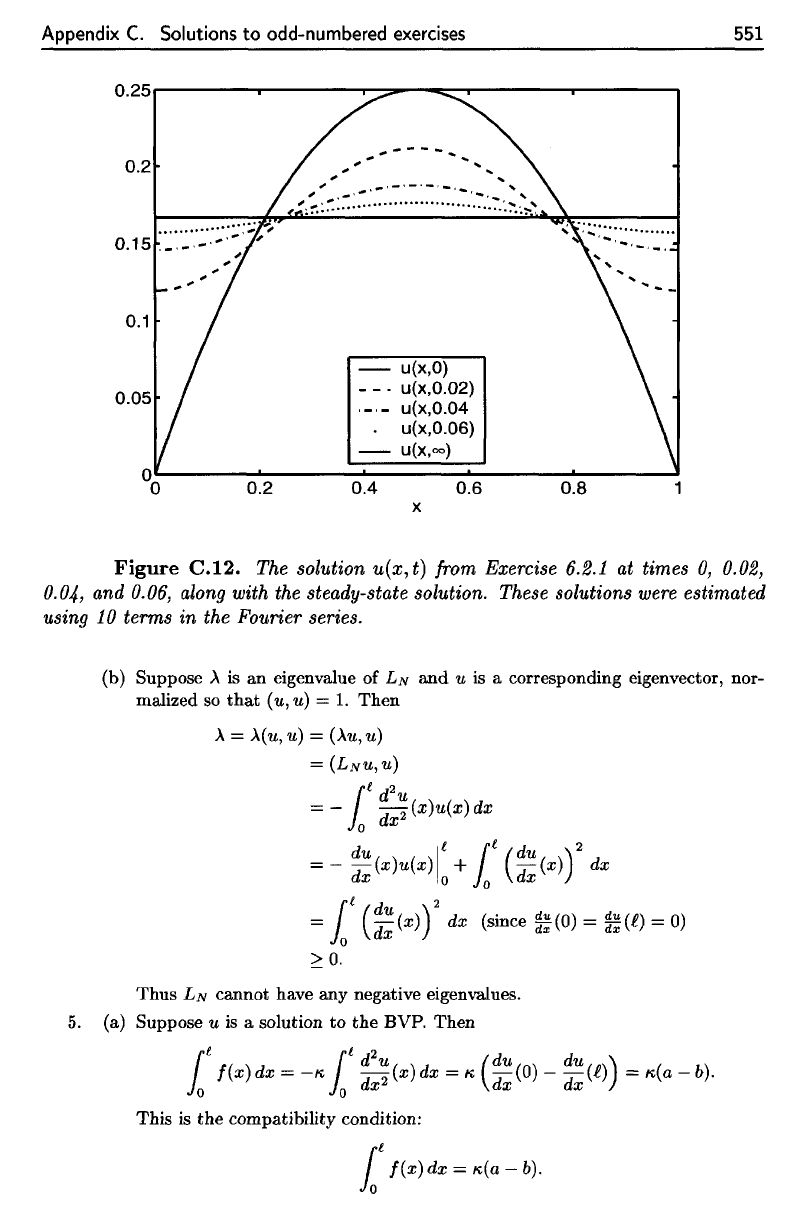
Appendix
C.
Solutions
to
odd-numbered
exercises
551
Figure
C.12.
The
solution
w(x,t)
from
Exercise
6.2.1
at
times
0,
0.02,
0.04,
and
0.06,
along
with
the
steady-state
solution.
These
solutions
were
estimated
using
10
terms
in the
Fourier
series.
(b)
Suppose
A is an
eigenvalue
of LN and
it
is a
corresponding eigenvector, nor-
malized
so
that
(u. u) =
1.
Then
Thus
LN
cannot have
any
negative eigenvalues.
5.
(a)
Suppose
u is a
solution
to the
BVP.
Then
This
is the
compatibility
condition:
Appendix
C.
Solutions
to
odd-numbered exercises
0.25,....----"T""""----r-~-~__r---~---___,
0.2
0.15.
__
,
....
0.1
0.2
...
----.,
..
..
...
..
...
"
,-
....
-
-'-'-
-'-
.........
"
'!:-::::
...............................
,:.':"'
...
~~
- u(x,O)
- - - u(x,0.02)
,-,
- u(x,0.04
u(x,0.06)
-
u(x,oo)
0.4 0.6
x
"--
0.8
551
Figure
C.12.
The solution
u(x,
t) from Exercise 6.2.1 at times
0,
0.02,
0.04, and 0.06,
along
with the steady-state solution. These solutions were estimated
using 10 terms in the Fourier series.
(b) Suppose A is an eigenvalue of LN
and
U is a corresponding eigenvector, nor-
malized
so
that
(u, u) =
1.
Then
A =
A(U,
u) =
(AU,
u)
= (LNU,U)
=
-it
::~
(x)u(x) dx
= -
~:(x)u(x)l:
+
1£
(::(X))2
dx
1
£ d 2
= 0
C:(x))
dx (since
~~(O)
=
~~(f)
=
0)
~
O.
Thus
LN
cannot have any negative eigenvalues.
5.
(a) Suppose U
is
a solution
to
the
BVP.
Then
if
I(x)dx
= -t>
it
::~(X)dX
=
t>
(::(0)
-
::(f))
=
t>(a
-
b).
This is
the
compatibility condition:
1£
I(x)
dx =
t>(a
-
b).

552
Appendix
C.
Solutions
to
odd-numbered
exercises
(b) The
operator
K
:
C^[0,£\
->•
C[Q,t\
defined
by
has
eigenpairs
The
method
of
Fourier series
can be
applied
to
show
that
a
unique solution
exists
for
each
/
G
C[0,^].
(The
key is
that
0 is not an
eigenvalue
of K, as it
is of
LN.)
7.
As
shown
in
this
section,
the
solution
to the
IBVP
is
where
do,
di,
c?2,
• • • are the
Fourier cosine
coefficients
of
if).
We
have
This last series certainly converges
(as can be
proved,
for
example, using
the
cora-
narisrm
t.pst^
anr\
This shows
that
The
limit
do is
the
average
of the
initial temperature distribution.
9.
The
steady-state
temperature
is
about
0.992 degrees Celsius.
11. (a)
Suppose
that
the
Fourier sine series
of
u(x,t)
on
(0,^)
is
and
u
satisfies
552
Appendix
C.
Solutions
to
odd-numbered exercises
(b)
The
operator K :
c1
[0,
f]
-t
C[O,
f] defined by
has eigenpairs
~n2~2
(n~x)
>'0
= 1,
'Yo(x)
=
1,
and
>'n
= 1 +
-;y-,
'Yn(x) = cos
-f-
, n =
1,2,3,
....
The
method
of Fourier series can
be
applied
to
show
that
a unique solution
exists for each
f E
C[O,
fl.
(The
key is
that
0 is not an eigenvalue of
K,
as
it
is of
LN.)
7. As shown in this section,
the
solution
to
the
IBVP
is
~
2 2
/l2
(n~x)
u(x, t) =
do
+
L...J
dne-
n
1T
t cos
-f-
,
n=l
where
do,
dl,
d
2
,
...
are
the
Fourier cosine coefficients of"p. We have
00
00
L
dne-n21T2t/l2
cos
(n;x)
~
L
JdnJ
e-n21T2t/l2Icos
(n;x)
I
n=l
n=l
n=l
00
~
e-1T2t/l2
L
JdnJ
e-(n
2
-1)1T
2
t/l
2
.
n=l
This last series certainly converges (as
can
be proved, for example, using
the
com-
parison test),
and
This shows
that
00
do
+ L
dne-n21T2t/£2
cos
(n;x)
-t
do
as t
-t
00.
n=l
The
limit
do
is
~
1£
"p(x)
dx,
the
average of
the
initial
temperature
distribution.
9.
The
steady-state
temperature
is
about
0.992 degrees Celsius.
11. (a) Suppose
that
the
Fourier sine series
of
u(x, t) on (0,
f)
is
00
it
u(x, t) = L an(t) sin
(n;x),
an
(t) =
~
u(x, t) sin
(n;x)
dx
n=l
0
and
u satisfies
au au
ax
(0, t) =
ax
(f, t) = 0 for all t >
o.

AnnpnHiv
C
Solutions
to
r»HH-nu
inhered
exerr.ises
553
The nth
Fourier sine
coefficient
of
—d
2
u/dx
2
is
computed
as
follows:
Since
the
values
w(0,
t)
and
u(l,
t) are
unknown,
we see
that
it is not
possible
to
express
the
Fourier sine
coefficients
of
—d
2
u/dx
2
in
terms
of
oi(t),a2(t),
—
(b)
The
Fourier sine series
of
u(x,
t) = t is
and the
formal
calculation
of the
sine series
of
—d
2
u/dx
2
yields
However,
and so all of the
Fourier sine coefficients
of
—d
2
u/dx
2
should
be
zero.
Thus
the
formal
calculation
is
wrong.
Section
6.3
1. The
formula
for the
solution
u is
exactly
the
same
as in
Example 6.6, with
a
different
value
for
K
(4.29 instead
of
3.17). This implies
that
the
amplitude
of the
solution
is
reduced
by
about 26%. Therefore, there
is
less variation
in the
temperature
distribution
in the
silver ring
as
opposed
to the
gold
ring.
3. fa) The
IBVP
is
Appendix
C.
Solutions
to
odd-numbered
exercises
553
The
nth
Fourier sine coefficient of -02U/OX
2
is
computed
as follows:
2 r
02U
. (n1l"x)
-"llo
ox
2
(x, t)
sm
-e-
dx
2
[ou
. (n1l"x)ll n1l"1
i
ou
(n1l"x)]
=
--
-(x,t)sm
- - -
-(x,t)cos
- dx
e
Ox
e 0 e 0
ox
e
2n1l"
r
ou
(n1l"x)
=£2
10
ox(x,t)cos
-e-
dx
2n1l"
[ (n1l"x)
Ii
n1l"
r . (n1l"x) ]
=
£2
u(x, t) cos
-e-
0 + f
10
u(x, t) sm
-e-
dx
2n1l"
n n
2
11"2
=
£2
((-1)
u(e, t) - u(O,t)) +
f2an(t).
Since
the
values
u(O,
t)
and
u(e, t) are unknown,
we
see
that
it is
not
possible
to
express
the
Fourier sine coefficients of -02U/OX
2
in
terms
of
al
(t), a2(t),
....
(b)
The
Fourier sine series of u(x, t) = t
is
00
2
(1
- (_1)n) t
'"'
sin (1mx),
~
n1l"
n=l
and
the
formal calculation of
the
sine series of -02U/OX
2
yields
00
L 2
(1
-
(-1t)
n1l"tsin
(n1l"x).
n=l
However,
02U
-
ox
2
(x,
t)
= 0,
and
so all of
the
Fourier sine coefficients of -02U/OX
2
should
be
zero.
Thus
the
formal calculation is wrong.
Section
6.3
1.
The
formula for
the
solution u is exactly
the
same as in Example 6.6,
with
a different
value for
fl,
(4.29 instead of 3.17). This implies
that
the
amplitude of
the
solution
is
reduced
by
about
26%. Therefore,
there
is less variation in
the
temperature
distribution in
the
silver ring as opposed to
the
gold ring.
3. (a)
The
IBVP
is
ou
02U
pc
at
-
fl,
ox
2
=
0,
-511"
< X <
511",
t > 0,
u(x,O) = "p(x),
-511"
< X <
511",
u(
-511",
t)
=
u(511",
t), t >
0,
ou ou
ox
(-511",
t)
=
ox
(511",
t), t >
O.

554
Appendix
C.
Solutions
to
odd-numbered
exercises
(b)
The
solution
is
where
(c)
The
steady-state
temperature
is the
constant
u
s
= 25 +
7T
4
/9
degrees
Celsius.
(d)
We
must choose
t so
that
holds
for
every
x €
[—STT,
STT].
By
trial
and
error,
we find
that
about
360
seconds
(6
minutes)
are
required.
5.
(a) To
show
that
L
p
is
symmetric,
we
perform
the now
familiar
calculation:
we
form
the
integral
(L
p
u,
v) and
integrate
by
parts twice
to
obtain
(u,
L
p
v).
The
boundary term
from
the first
integration
by
parts
is
Since
both
u and v
satisfy periodic boundary conditions,
we
have
so
the
boundary term vanishes.
The
boundary term
from
the
second integra-
tion
by
parts
vanishes
for
exactly
the
same reason.
(b)
Suppose
L
p
u
=
\u,
where
u has
been normalized:
(u, u) = 1.
Then
The
boundary terms vanishes because
of the
periodic boundary conditions:
7.
(a)
Since
the
ring
is
completely insulated,
a
steady-state temperature distribution
cannot exist unless
the net
amount
of
heat being added
to the
ring
is
zero.
This
is
exactly
the
same situation
as a
straight
bar
with
the
ends,
as
well
as
the
sides, insulated.
554 Appendix
C.
Solutions
to
odd-numbered exercises
(b)
The
solution is
00
"n2
t
(nx)
u(x, t) =
Co
+ L
ene-25P""C
cos
""5
'
n=l
where
71"4
Co
=
25
+
9'
10(
_l)n+l
en
= n
4
'
n =
1,
2,3,
....
( c)
The
steady-state
temperature
is
the
constant
Us
=
25
+
71"4/9
degrees Celsius.
(d) We
must
choose t so
that
Ius
- u(x,
t)1
< 0.01
lusl
-
holds for every x E
[-571",571"].
By
trial
and
error, we find
that
about
360
seconds (6 minutes)
are
required.
5.
(a) To show
that
Lp
is symmetric, we perform
the
now familiar calculation: we
form
the
integral (Lpu, v)
and
integrate
by
parts
twice
to
obtain
(u, Lpv).
The
boundary
term
from
the
first integration
by
parts
is
[
du
]l
du
du
- dx (x )v(x)
-t
=
dx
(-f)v(
-f)
-
dx
(f)v(f).
Since
both
u
and
v satisfy periodic
boundary
conditions, we have
du du
v(
-f)
= v(f), dx
(-f)
= dx
(f),
so
the
boundary
term
vanishes.
The
boundary
term
from
the
second integra-
tion
by
parts
vanishes for exactly
the
same
reason.
(b) Suppose
Lpu =
AU,
where u has been normalized: (u,
u)
= 1.
Then
1
£
d2U
A =
A(U,
u)
=
(Au,
u)
= (Lpu, u) = -
_£
dx
2
(x)u(x)
dx
= -
[~:(x)u(x)rl
+
I:
(~:(x)f
dx
=
I:
(~:(x)f
dx
~
O.
The
boundary
terms
vanishes because
of
the
periodic
boundary
conditions:
du du
dx
(-f)u(
-f)
= dx
(f)u(f).
7.
(a) Since
the
ring
is
completely insulated, a
steady-state
temperature
distribution
cannot
exist unless
the
net
amount
of
heat
being
added
to
the
ring is zero.
This
is exactly
the
same
situation
as a
straight
bar
with
the
ends, as well
as
the
sides, insulated.

Appendix
C.
Solutions
to
odd-numbered
exercises
555
(b)
Suppose
u
is a
solution
to
(6.21).
Then
The
last
step
follows from the
periodic boundary conditions.
(c)
The
negative second derivative operator, subject
to
boundary conditions,
has a
nontrivial
null space, namely,
the
space
of all
constant
functions
on
(—i,i).
In
analogy
to the
Predholm
alternative
for
symmetric matrices,
we
would expect
a
solution
to the
boundary value problem
to
exist
if and
only
if the
right-hand-
side
function
is
orthogonal
to
this
null
space. This condition
is
Thus
Gx = 0
implies
that
the
vector
or
simply
Section
6.4
1.
We
give
the
proof
for
the
general case
of a
Gram matrix
G.
Suppose
Gx = 0,
where
x €
R
n
.
Then
(x, Gx) = 0
must hold,
and
Appendix
C.
Solutions
to
odd-numbered exercises
555
(b) Suppose U is a solution
to
(6.21).
Then
I
t
1£
0
2
f(x)
dx =
-K,
ax~
(x,
t)
dx
-i
-i
[
aU
] l
=
-K,
-(x,t)
ax
-l
(
aU
aU)
=K,
ax(-l,t)-
ax(l,t)
=0.
The
last step follows from
the
periodic boundary conditions.
(c)
The
negative second derivative operator, subject
to
boundary
conditions, has a
nontrivial null space, namely,
the
space of all constant functions on
(-l,
l).
In
analogy
to
the
Fredholm alternative for symmetric matrices,
we
would expect
a solution
to
the
boundary value problem
to
exist
if
and
only if
the
right-hand-
side function
is
orthogonal
to
this null space. This condition is
or simply
Section 6.4
I:
cf(x)
dx = 0 for all c E
R,
t
f(x)dx
=
o.
J-
l
1. We give
the
proof for
the
general case of a
Gram
matrix
G. Suppose
Gx
=
0,
where
x
ERn.
Then
(x,
Gx)
= 0 must hold,
and
n n n
(x,
Gx)
=
Z)GX)iXi
= L L
GijXjXi
i=1
Thus
Gx
= 0 implies
that
the
vector
n
i=1
j=1
n n
i=1
j=1
=
~
(tXjUj,Ui)
Ui
(t
XjUj,
~
XiUi)
n
=
LXjUj
j=1
2
LXjUj
j=1

556
Appendix
C.
Solutions
to
odd-numbered
exercises
is
the
zero vector. But, since
{wi,
W2,...
,u
n
}
is
linearly independent, this
in
turn
implies
that
x\
=
xi
= • • • =
x
n
= 0,
that
is,
that
x = 0.
Since
the
only
vector
x €
R
n
satisfying
Gx = 0 is the
zero vector,
G is
nonsingular.
3. (a)
that
is,
and
similarly
for
c(x)
and
K(X).
Then
the
IBVP
is
5.
(a)
Write
pi
=
8.97,
p
2
=
7.88,
(b)
The
mass matrix
M
is
tridiagonal
and
symmetric,
and its
nonzero
entries
are
and
The
stiffness
matrix
K is
tridiagonal
and
symmetric,
and its
nonzero entries
are
and
(b)
The
system
of
ODEs
is
556
Appendix
C.
Solutions
to
odd-numbered
exercises
is
the
zero vector.
But,
since
{U1,
U2,
...
, Un} is linearly independent, this in
turn
implies
that
Xl
=
X2
= ... =
Xn
=
0,
that
is,
that
x =
0.
Since
the
only vector
x
E R
n
satisfying
Gx
= ° is
the
zero vector, G is nonsingular.
3. (a)
_ [
2/9
M-
1/18
1/18]
K = [ 6
2/9'
-3
-3]
f
__
1_ [
11
cos (t) ]
6 ' (t) -
162
11
cos (t) .
(b)
The
system of ODEs is
do:
M dt =
-Ko:
+ f(t),
that
is,
2
d0:
1
1
d0:2
11
cos (t)
9"
d.t
+
18
d.t
= -60:1 +
30:2
+ 162 '
.!..
d0:
1
~
d0:2
_ 3 _ 6
11
cos (t)
18
dt + 9 dt -
0:1
0:2
+ 162 .
5.
(a) Write
P1
= 8.97,
P2
= 7.88,
p(x) = {
° < X < 50,
50
< x < 100,
and
similarly for c(x)
and
,.(x).
Then
the
IBVP
is
aU
a ( aU)
p(x)c(x)
at - ax ,.(x) ax =
0,
° < x < 100,
u(x,O) = 5, ° < x < 100,
u(O,t) =
0,
t >
0,
u(100, t) =
0,
t >
0.
t >
0,
(b)
The
mass
matrix
M is tridiagonal
and
symmetric,
and
its
nonzero entries are
and
{
~
6 '
Mi,i+1=
~
i =
1,2,
...
,
~
-
1,
i =
~,~
+ 1,
...
, n -
1,
M;;
= {
6 '
~
3 '
(Pi
C1
+P2C2
)h
3
i =
1,2,
...
,
~
- 1,
. n
2 =
2'
~
'-n+1n+2
1
3'
2-
2
'2
,
...
,n-.
The
stiffness
matrix
K is tridiagonal
and
symmetric,
and
its nonzero entries
are
and
h'
K"+l
=
{
-~
1.,1.
~2
K;; = {
-h'
~
h '
1<1+1<2
h '
~
h '
i = 1,2,
...
,
~
-
1,
i =
~,
~
+
1,
...
, n
-1,
i = 1,2,
...
,
~
- 1,
i
=~,
i =
~
+ 1, % +
2,
...
, n - 1.
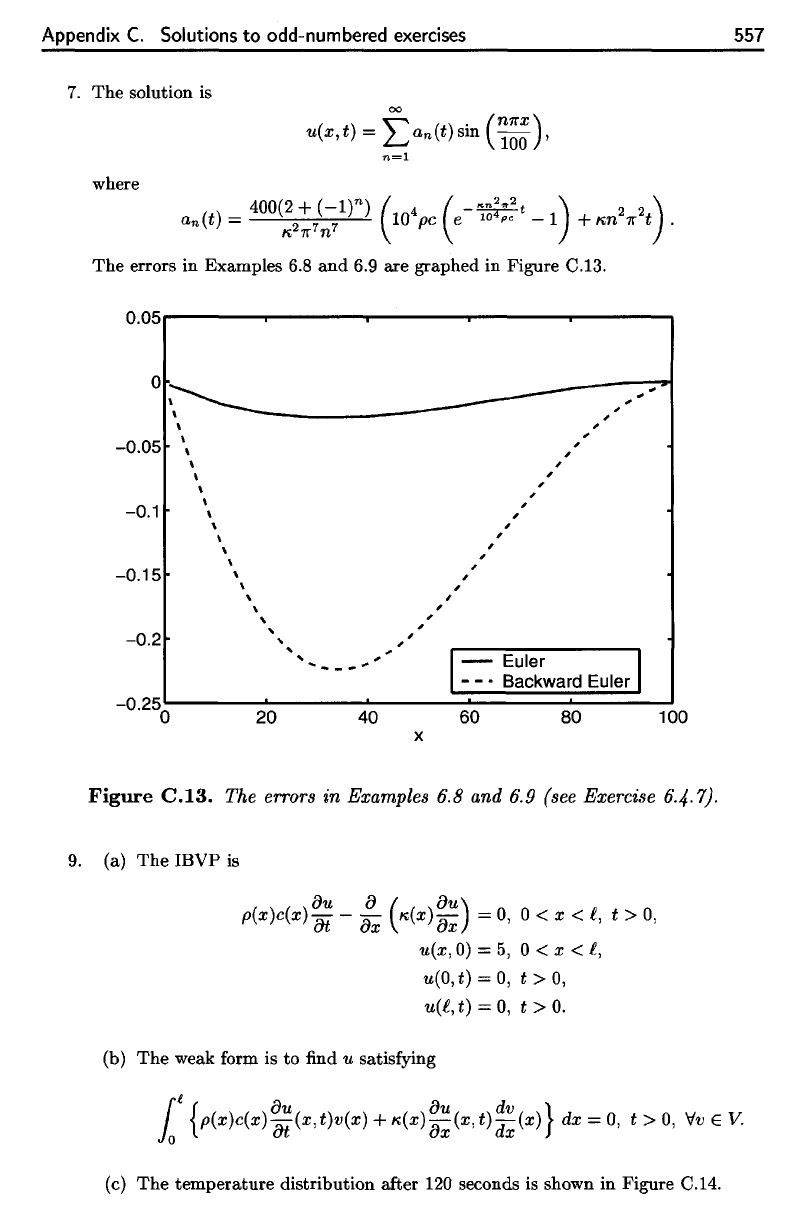
Appendix
C.
Solutions
to
odd-numbered
exercises
557
7.
The
solution
is
where
Figure
C.13.
The
errors
in
Examples
6.8 and 6.9
(see Exercise
6.4-V-
9.
(a)
ThelBVPis
(b)
The
weak
form
is to find u
satisfying
(c)
The
temperature distribution
after
120
seconds
is
shown
in
Figure
C.14.
The
errors
in
Examples
6.8 and 6.9 are
graphed
in
Figure C.13.
Appendix
C.
Solutions
to
odd-numbered exercises
7.
The
solution is
00
u(x,t)
=
I>n(t)
sin
C~;),
n=l
where
a
n
(t)
__
400(2+(-1)n)
( 4 (
"n
2
,,2t
) 2
2)
10
pc e
-~
-1
+ Kn 7r t .
K
2
7r
7
n
7
The
errors in Examples 6.8
and
6.9 are graphed in Figure C.13.
0.05,.----..-----.....----....----...,......----,
°l~
____
~
..
..
..
..
-0.05
-0.1
-0.15
-0.2
,
\ '
\ "
\ ,
\ ,
\ ,
\ ,
\ ,
" '
"
..
"
,
,
,
,
,
,
,
..
..
,
,
l
-
Euler I
-
_.
Backward Euler
" "
....
_-_ ....
20
40
60
80
x
100
Figure
C.I3.
The errors in Examples 6.8 and 6.9 (see Exercise 6.4.7).
9.
(a)
The
IBVP
is
au
a (
aU)
p(x)c(x)
at
-
ax
K(X)
ax
= 0, 0 < x <
t',
t >
0,
u(x,O)
=
5,
0 < x <
t',
u(O, t) = 0, t >
0,
u(t', t) =
0,
t >
O.
(b)
The
weak form is
to
find u satisfying
557
l
l{ & &
~
}
o
p(x)c(x)
at
(x,
t)v(x)
+
K(X)
ax
(x, t)
dx
(x)
dx
= 0, t > 0, \Iv E V.
(c)
The
temperature
distribution after 120 seconds is shown in Figure C.14.
