Gockenbach M.S. Partial Differential Equations. Analytical and Numerical Methods
Подождите немного. Документ загружается.


538
Appendix
C.
Solutions
to
odd-numbered
exercises
that
is,
Then
A*,,
A;
= 1,
2,...,
are
eigenvalues,
and the
corresponding eigenfunctions
are
Using
Newton's method,
we find
that
which
yields
The
eigenfunctions
are
vi,vz,
as
given
by the
above
formula.
A
direct calculation shows
that
so
vi
and
v?
are not
orthogonal.
The
errors
in
approximating
the
original
functions
using
10
terms
of the
Fourier sine
series
are
graphed
in
Figure
C.6.
9.
sin
(STTX)
(That
is, all of the
Fourier sine
coefficients
are
zero,
except
the
third, which
is
one.)
11.
The
series have
the
form
where
The
errors
in
approximating
the
original functions using
10
terms
of the
Fourier
quarter-wave
cosine series
are
graphed
in
Figure
C.7.
538
Appendix
C.
Solutions
to
odd-numbered exercises
that
is,
2
21
Ak
= 8
k
+
4'
k = 1,2,
....
Then
Ak,
k = 1,2,
...
, are eigenvalues,
and
the
corresponding eigenfunctions are
Using Newton's method,
we
find
that
81
==
1.8366, 8
2
==
4.8158,
which yields
Al
==
8.6231,
A2
==
28.4423.
The
eigenfunctions are
VI,
V2,
as given by
the
above formula.
A direct calculation shows
that
so
VI
and
V2 are not orthogonal.
(a)
,",00
2(
_l)n+l
. ( )
7.
L....n=1
mr
sm
n7rX
(b)
,",00
4sin(Vf)
. ( )
L....n=1
n2".2
SIn
n7rX
(
)
,",00
12(_I)n+l
. ( )
c
L....n=l
n3".3
sIn
n7rX
(d)
,",00
720(
_I)n+l
. ( )
L....n=l
n5".o
SIn
n7rX
The
errors in approximating
the
original functions using
10
terms
of
the
Fourier sine
series are graphed in Figure C.6.
9.
sin
(37rx)
(That
is, all of
the
Fourier sine coefficients are zero, except
the
third, which
is one.)
11.
The
series have
the
form
~
((2n
-1)7rX)
L...Ja
n
cos 2 '
n=l
where
(b)
-
32cos
«2n-I)"./4)
sin
2
«2n-I)"./8).
an -
".2(2n_l)2
,
(d)
8
5760+2880(
_l)n
(2n-I)".+240(2n-l)2".2+
7
(2n_l)4".4
an = -
".
(2n-l)
The
errors in approximating
the
original functions using
10
terms
of
the
Fourier
quarter-wave cosine series are graphed in Figure C.7.
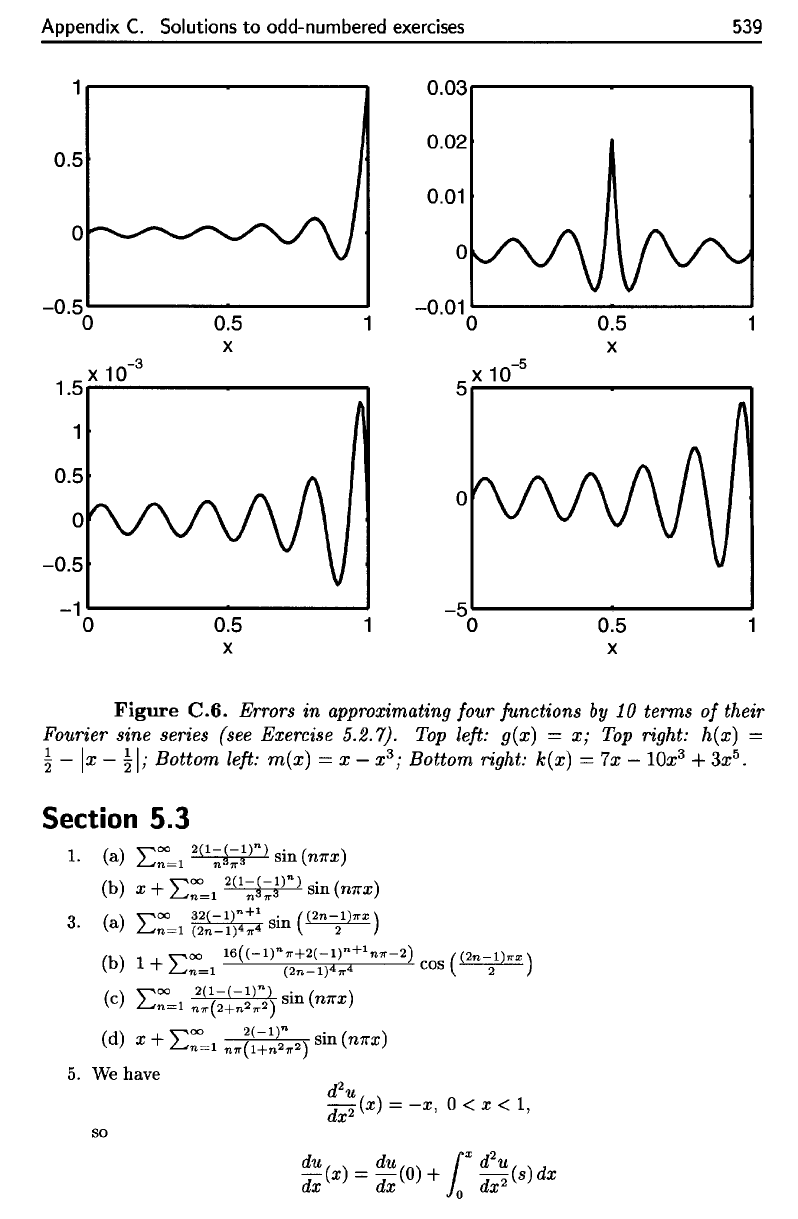
Appendix
C.
Solutions
to
odd-numbered
exercises
539
so
Figure
C.6.
Errors
in
approximating
four
functions
by 10
terms
of
their
Fourier sine series (see Exercise 5.2.7).
Top
left:
g(x)
= x; Top
right:
h(x)
=
|
—
x
—
|
;
Bottom
left:
m(x]
=
x
—
x
3
;
Bottom
right: k(x)
=7x
—
10x
3
Section
5.3
5.
We
have
Appendix
C.
Solutions
to
odd-numbered exercises 539
1~------------------~
0.03,....---------
.....
0.02
0.5
0.01
-0.5
-0.01
0 0.5 1 0 0.5
x
x
1.5 x 10
-3
5
X1O
-5
1
-1~----------------~
o
-5~----------------~
0.5
x
1
o
0.5
x
1
Figure
C.6.
Errors in approximating four /unctions
by
10 terms
of
their
Fourier sine series (see Exercise
5.2.7).
Top
left: g(x) =
x;
Top
right: h(x) =
~
-
Ix
-
~
I;
Bottom left:
m(x)
= x - x
3
;
Bottom right: k{x) = 7x - lOx
3
+
3x
5
•
Section 5.3
1 (a)
~oo
2(1_~_1)n)
. ( )
.
L..-n=l
n
.".3
Sln
n7rX
(b)
~oo
2(1-C-l)n)
. ( )
x +
L..-n=l
n3.".3 sm
n7rX
3 (a)
~oo
32(_1)n+l
sin
(2n-l).".X)
.
L..-n=l
(2n_l)4.".4
2
(
b) 1
~oo
16(-1)n.".+2(-1)n+l
n
.".-2)
cos
(2n-l)"X)
+
L..-n=l
(2n-l)411'4
2
(c) L
OO
2(1-(-1)n)
sin (n7rx)
n=l
nn-(2+n27r2)
d
2
u
dX2
(x)
=
-x,
0 < x <
1,
so
540
Appendix
C.
Solutions
to
odd-numbered exercises
Finally,
we
choose
C so
that
u(l)
= 0,
which
yields
C =
1/6.
This
yields
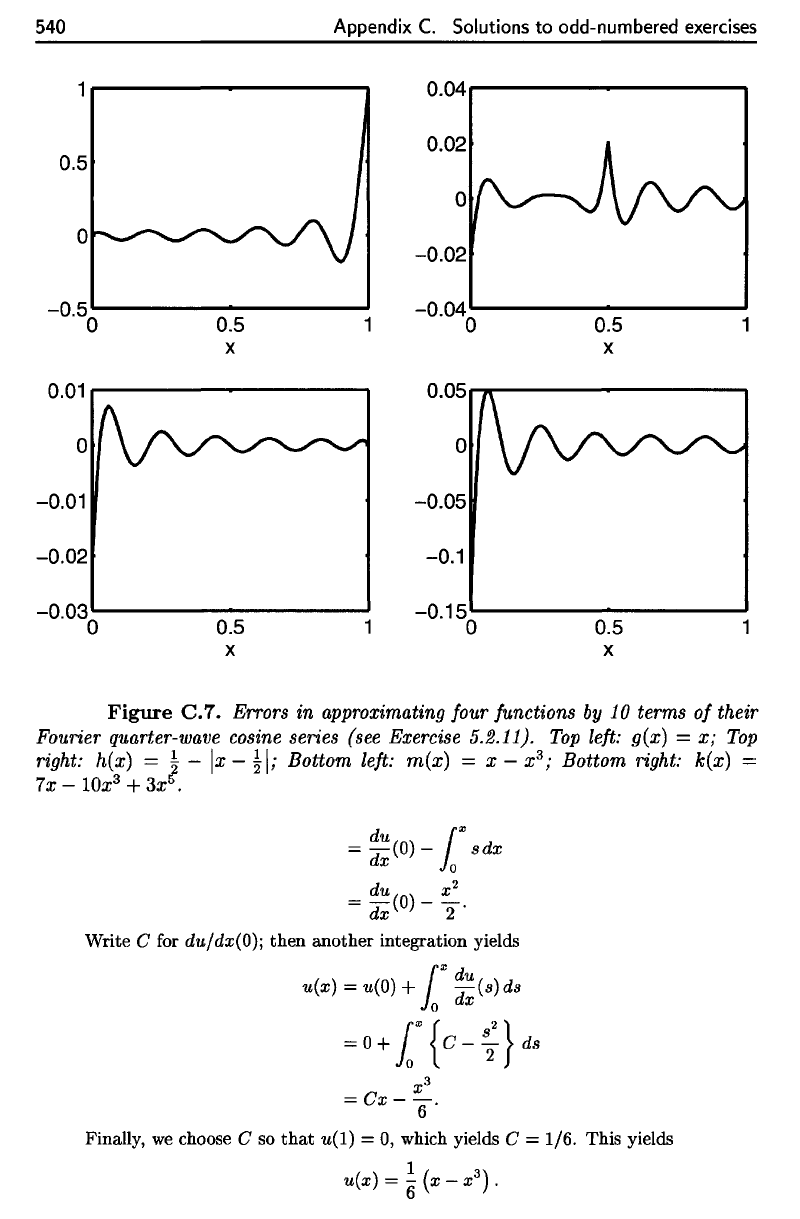
Figure
C.7.
Errors
in
approximating four functions
by 10
terms
of
their
Fourier quarter-wave cosine series (see Exercise 5.2.11).
Top
left:
g(x)
=
x;
Top
right:
h(x)
=
\
— x
—\
;
Bottom
left:
m(x)
= x
—
x
3
;
Bottom
right:
k(x]
=
7x-Wx
3
+3x
5
.
Write
C for
du/dx(Q);
then
another
integration
yields
540
Appendix
C.
Solutions
to
odd-numbered
exercises
0.04,....----------"
0.5
-0.5'----------~
o 0.5
1
x
0.01
,....----------"
o
-0.01
-0.02
-0.03'----------~
o
0.5
x
1
-0.02
-0.04
0
0.05
0
-0.05
-0.1
-0.15
0
0.5
x
0.5
x
1
Figure
C.7.
Errors
in
approximating four junctions
by
10 terms
of
their
Fourier quarter-wave cosine series (see Exercise
5.2.11).
Top
left: g(x) = X;
Top
right: h(x) = ! -
Ix
- !
I;
Bottom left:
m(x)
= x - x
3
;
Bottom
right: k(x) =
7x
- lOx
3
+
3xt.
du
1'"
=
-(0)
-
sdx
dx 0
=
~:(O)
_
x22.
Write C for du/dx(O); then another integration yields
l
"'d
u(x)=u(O)+
0
d;(s)ds
= 0 +
1'"
{c
-
s;
} ds
x
3
=Cx-
6
·
Finally,
we
choose C
so
that
u(l)
=
0,
which yields C = 1/6. This yields
u(x)
=
~
(x-x
3
).

Using
integration
by
parts
twice, almost exactly
as in
(5.23),
we can
express
&„
in
terms
of
a
n
:
Appendix
C.
Solutions
to
odd-numbered
exercises
541
7.
The
Fourier quarter-wave sine
coefficients
of
—Td
2
u/dx
2
are
while
those
of u are
This
gives
the
desired result. (Actually, since
it is
known
that
the
negative second
derivative operator
is
symmetric under
the
mixed boundary conditions,
we can
just
appeal
to
(5.29),
which
is the
above calculation written
abstractly.)
9.
Let
ai,
0,2,as,...
be the
Fourier
quarter-wave
sine
coefficients
of u;
then
where
K
=
3/2.
We
also have
Appendix
C.
Solutions
to
odd-numbered exercises
541
7.
The
Fourier quarter-wave sine coefficients
of
-Td
2
u/dx
2
are
b
= _
2T
1i
d
2
u(
) .
((2n
-l)'JrX)
d
n £ 0 dx2 x sm
2£
x,
while those
of
u
are
2 . (2n - l)7rx
1
i ( )
an = £ 0
u(x)sm
2£
dx.
Using integration by
parts
twice, almost exactly as in (5.23), we
can
express b
n
in
terms
of
an:
_
2T
1t
d
2
u(
).
((2n-1)7rx)
d
£ 0 dx
2
x
sm
2£
x
= _
2T
{
[dU
(x) sin
((2n
-
l)7rX)]
i
£ dx 2f
x=O
_ (2n
-1)7r
ii
du()
((2n
-l)7rX)
d }
n d X cos n X
2"
0 X
2"
=
2T(2n
-1)7r
1i
du()
((2n
-l)7rX)
d
2£2
odxxCOS
2f x
(since sin (0) =
du/dx(£)
= 0)
=
2T(2n
-1)7r
{[
()
((2n
-l)7rX)]
i
2£2
u X cos
2£
,,=0
(2n
-1)7r
1t
(
).
((2n
-l)7rX)
d }
+ 2f
ux
sm
2£
x
o
_
T(2n
_1)27r
2
~
1i
( ) .
((2n
- l)7rX) d
-
4£2
£
uxsm
2£
x
o
(since
u(O)
= cos ((2n - 1)7r/2) = 0)
This
gives
the
desired result. (Actually, since
it
is known
that
the
negative second
derivative
operator
is symmetric
under
the
mixed
boundary
conditions, we
can
just
appeal
to
(5.29), which is
the
above calculation
written
abstractly.)
9. Let
aI,
a2, a3, .
..
be
the
Fourier quarter-wave sine coefficients
of
U;
then
_ d
2
u(
) =
~
,..(2n _1)27r
2
in
((2n
-l)7rX)
,..
dX2
x
~
2002
an s
200
'
n=l
where,.. =
3/2.
We also have
0.001 =
~
0.004 sin
((2n-1)7rX).
~
(2n -
1)7r
200
n=l
542
Appendix
C.
Solutions
to
odd-numbered exercises
Setting
the two
series equal
and
solving
for
a
n
,
we find
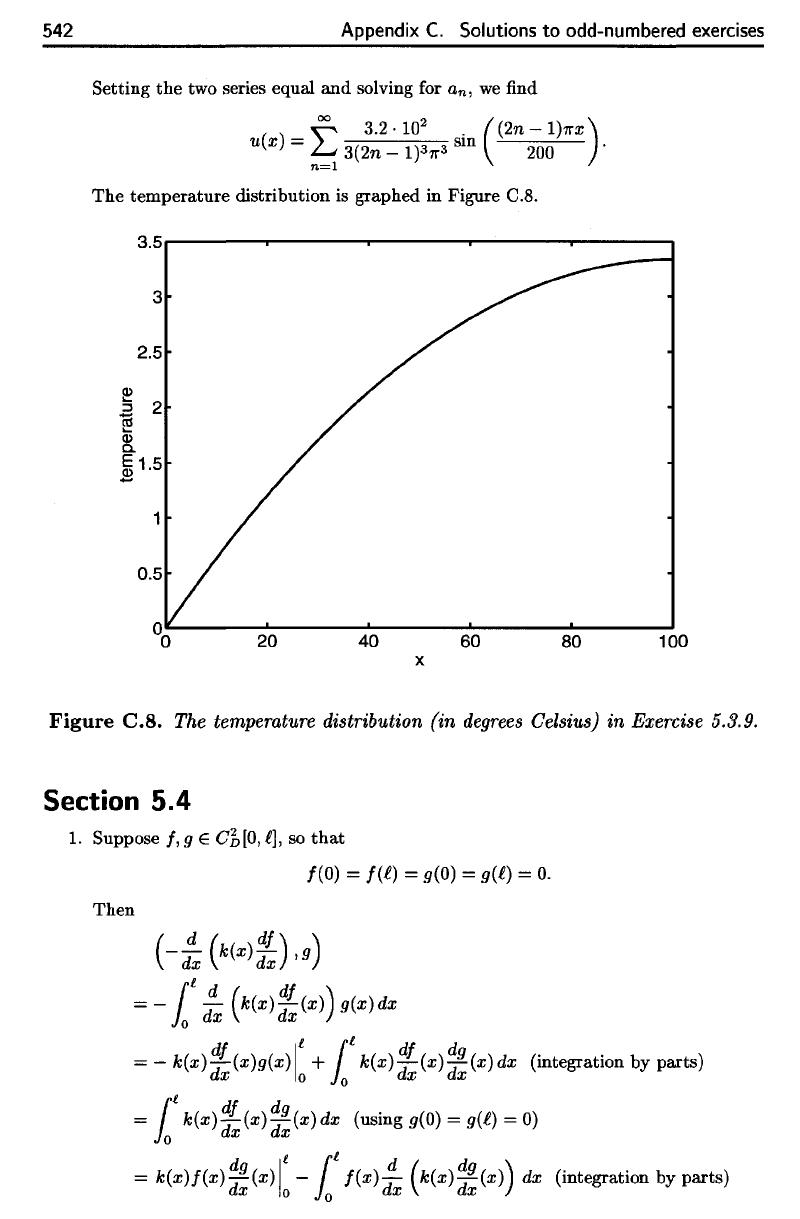
The
temperature distribution
is
graphed
in
Figure
C.8.
Figure
C.8.
The
temperature distribution
(in
degrees
Celsius)
in
Exercise 5.3.9.
Section
5.4
1.
Suppose
f,g
<E
Cr>[0,<],
so
that
Then
542
Appendix
C.
Solutions
to
odd-numbered exercises
Setting
the
two series equal
and
solving for an,
we
find
~
3.2.10
2
.
(2n-1)7rx)
u(x) =
~
3(2n _
1)37r3
sm 200 .
The
temperature
distribution is graphed in Figure C.S.
3.5r-----r-----r-----~---...__--__,
3
2.5
Q)
:s
2
~
Q)
c.
~
1.5
0.5
20
40
60 80
100
x
Figure
C.S.
The temperature distribution (in
degrees
Celsius) in Exercise 5.3.9.
Section 5.4
1. Suppose
I,
9 E
C1[0,
€J,
so
that
1(0) = f(€) =
g(O)
=
g(€)
=
O.
Then
(-!
(k(X):~)
,g)
=-li
d~
(k(x):~(x))9(X)dX
df
Ii
1i
df d
=-k(x)dx(x)g(x)
0 + 0
k(x)dx(x)d;(x)dx
(integration by parts)
1
i
dl
d
= 0 k(x)
dx(x)
d~(x)dx
(using
g(O)
=
g(€)
=
0)
=
k(x)/(x)~;(x)l:
-It
f(x)!
(k(X)~;(X))
dx (integration by parts)

Appendix
C.
Solutions
to
odd-numbered
exercises
543
3.
Take p(x)
= (x
—
c)
3
(d
—
x)
3
and
V[
c>
d]
as
suggested
in the
hint.
5.
Repeating
the
calculation beginning
on
page 173,
we
obtain
This shows
that
derivative with respect
to
time
of the
total
energy
is
always negative,
and
hence
that
the
total energy
is
always decreasing.
Section
5.5
1. (a)
Yes.
(b)
No,
o(/,
/) = 0
for
/(x)
= 1, but /
/
0.
(c)
No,
o(/,
/) = 0
for
f(x)
= 1, but /
/
0.
3.
(a) The set S is the
span
of
{x,
x
2
}
and
therefore
is a
subspace.
(b)
As
discussed
in the
text,
a(-,-)
automatically satisfies
two of the
properties
of
an
inner product. Every
function
p in S
satisfies
p(Q)
= 0, so
a(-,
•)
also
satisfies
the
third property
(a(u,
u)
= 0
implies
that
u = 0) for
exactly
the
same reason
as
given
in the
text
for the
subspace
V
(see page 181).
(c)
The
best approximation
is
p(x)
= (9
—
3e)x
2
+ (4e
—
10)x.
(d)
The
bilinear
form
is not an
inner product
on
7>2,
since
a(l,
1) = 0 but
1/0
(a
constant
is
"invisible"
to the
energy inner product
and
norm). Therefore,
every
polynomial
of the
form
(9
—
3e)o;
2
+ (4e
—
10)x
+ C € S is
equidistant
from
f(x)
=
e
x
in the
energy
norm.
5.
Write
p(x]
— x(l — x) and
q(x)
—
x(l/2
—
x)(l
— x). The
approximation
will
be
v(x)
=
mp(x)
+
u-2q(x),
where
Ku = f. The
stiffness
matrix
K is
and the
load vector
f is
Therefore,
Appendix
C.
Solutions
to
odd-numbered exercises
=
-11
I(x)!
(k(x)
~~
(x))
dx (using 1(0) =
I(t)
=
0)
=
(/,-
d~
(k(x)~~)).
3. Take p(x) = (x - c)3(d - x)3
and
V[c,d] as suggested in
the
hint.
5. Repeating
the
calculation beginning on page 173,
we
obtain
!
[~lt
Ap(x)
(~f
dx+
~
1t
Ak(x)
(~;f
dX]
1
£
au
2
= - 0 c (
at)
dx, t >
O.
543
This shows
that
derivative with respect
to
time
of
the
total
energy is always negative,
and
hence
that
the
total
energy is always decreasing.
Section 5.5
1. (a) Yes.
(b) No,
a(f,
f)
= 0 for
I(x)
=
1,
but
I
i=
O.
(c) No,
a(f,
f)
= 0 for
I(x)
=
1,
but
I
i=
O.
3. (a)
The
set S is
the
span of
{x,
x
2
}
and
therefore is a subspace.
(b) As discussed in
the
text, a(·,·) automatically satisfies two of
the
properties
of an inner product. Every function
p in S satisfies
p(O)
=
0,
so a(·,·) also
satisfies
the
third
property (a(u,u) = 0 implies
that
u = 0) for exactly
the
same reason as given in
the
text
for
the
subspace V (see page 181).
(c)
The
best approximation is p(x) =
(9
- 3e)x2 +
(4e
- 10)x.
(d)
The
bilinear form is not
an
inner product on P2, since
a(l,
1) = 0
but
1
i=
0
(a
constant is "invisible"
to
the
energy inner
product
and
norm). Therefore,
every polynomial of
the
form
(9
- 3e)x2 +
(4e
- 10)x + C E S is equidistant
from
I(x)
=
eX
in the energy norm.
5.
Write p(x) =
x(l
- x)
and
q(x) =
x(1/2
-
x)(l
- x).
The
approximation will be
vex) =
U1P(X)
+
U2q(X),
where
Ku
=
f.
The
stiffness
matrix
K is
K = [
1:(1
+x)*(x)*(x)dx
1:(1
+x)~(x)*(x)dx
1
10
1
(1
+
x)*(x)~(x)
dx
10
1
(1
+
x)~(x)~(x)
dx
=
[-~
-t],
and
the
load vector f is
Therefore,
12
f=
[f~XP(X)dX]
= [
10
xq(x)dx
1 ]
1 .
-120
0.16412 ]
-0.038168 .
544
Appendix
C.
Solutions
to
odd-numbered
exercises
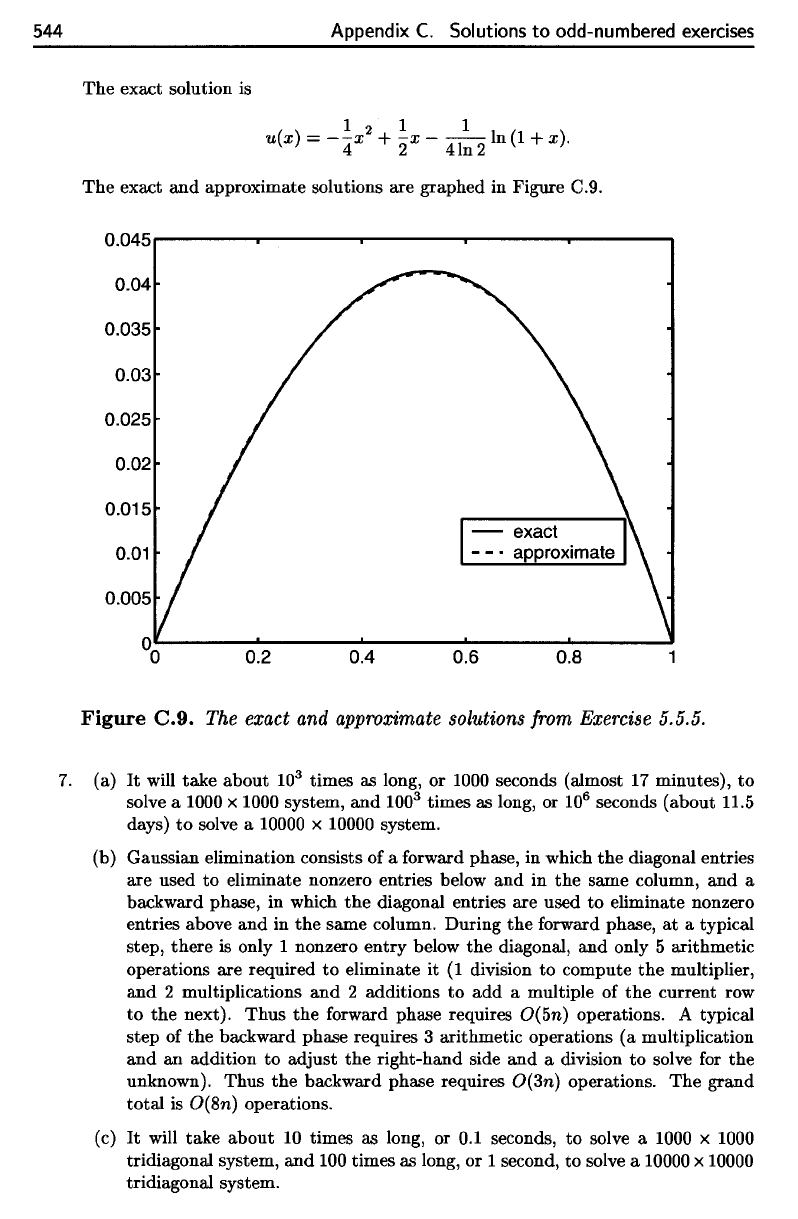
The
exact solution
is
Figure
C.9.
The
exact
and
approximate
solutions
from
Exercise
5.5.5.
7.
(a) It
will
take about
10
3
times
as
long,
or
1000 seconds (almost
17
minutes),
to
solve
a
1000
x
1000 system,
and
100
3
times
as
long,
or
10
6
seconds (about 11.5
days)
to
solve
a
10000
x
10000 system.
(b)
Gaussian elimination consists
of a
forward
phase,
in
which
the
diagonal entries
are
used
to
eliminate nonzero entries below
and in the
same column,
and a
backward
phase,
in
which
the
diagonal entries
are
used
to
eliminate nonzero
entries above
and in the
same column. During
the
forward
phase,
at a
typical
step, there
is
only
1
nonzero entry below
the
diagonal,
and
only
5
arithmetic
operations
are
required
to
eliminate
it (1
division
to
compute
the
multiplier,
and 2
multiplications
and 2
additions
to add a
multiple
of the
current
row
to the
next). Thus
the
forward
phase requires
O(5n)
operations.
A
typical
step
of the
backward phase requires
3
arithmetic operations
(a
multiplication
and an
addition
to
adjust
the
right-hand side
and a
division
to
solve
for the
unknown).
Thus
the
backward phase requires
O(3n)
operations.
The
grand
total
is
O(8n)
operations.
(c)
It
will
take about
10
times
as
long,
or 0.1
seconds,
to
solve
a
1000
x
1000
tridiagonal system,
and 100
times
as
long,
or 1
second,
to
solve
a
10000
x
10000
tridiagonal system.
The
exact
and
approximate solutions
are
graphed
in
Figure
C.9.
544 Appendix
C.
Solutions
to
odd-numbered exercises
The
exact solution is
1
2 1 1
u(x)
=
--x
+
-x
-
--In
(1
+ x)
4 2
4ln2
.
The
exact
and
approximate solutions are graphed in Figure C.g.
0.045r-----r-----r-----r-----r----~
0.04
0.035
0.03
0.025
0.02
0.015
0.01
0.2
0.4 0.6
exact
approximate
0.8
Figure
C.9.
The exact and approximate solutions from Exercise 5.5.5.
7.
(a)
It
will take
about
10
3
times as long,
or
1000 seconds (almost
17
minutes),
to
solve a 1000 x 1000 system,
and
100
3
times as long, or
10
6
seconds (about 11.5
days)
to
solve a 10000 x 10000 system.
(b) Gaussian elimination consists of a forward phase, in which
the
diagonal entries
are
used
to
eliminate nonzero entries below
and
in
the
same column,
and
a
backward phase, in which
the
diagonal entries are used
to
eliminate nonzero
entries above
and
in
the
same column. During
the
forward phase,
at
a typical
step,
there
is only 1 nonzero
entry
below
the
diagonal,
and
only 5 arithmetic
operations are required
to
eliminate
it
(1
division
to
compute
the
multiplier,
and
2 multiplications
and
2 additions
to
add
a multiple of
the
current row
to
the
next).
Thus
the
forward phase requires O(5n) operations. A typical
step of
the
backward phase requires 3 arithmetic operations (a multiplication
and
an
addition
to
adjust
the
right-hand side
and
a division
to
solve for
the
unknown). Thus
the
backward phase requires O(3n) operations.
The
grand
total
is O(Sn) operations.
(c)
It
will take
about
10
times as long, or 0.1 seconds,
to
solve a 1000 x 1000
tridiagonal system,
and
100 times as long, or 1 second,
to
solve a 10000 x 10000
tridiagonal system.

Appendix
C.
Solutions
to
odd-numbered
exercises
545
Section
5.6
1. (b)
Here
are the
errors
for n = 10,
20,40,
80:
n
10
20
40
80
maximum error
1.6586
4.3226
1.1036
2.7881
10~
3
10~
4
io-
4
10~
5
3. The
exact solution
is
u(x)
—
x(l
—
x
)/12. Here
are the
errors
for n
=
10,
20,40,80:
n
10
20
40
80
maximum error
1.1286
•
10~
3
2.9710
•
10~
4
7.6186
•
10~
&
1.9288
•
10~
&
5.
The
weak
form
is
The
bilinear
form
is
Section
5.7
We
see
that,
when
n is
doubled,
the
error decreases
by a
factor
of
approximately
four.
Thus
We
see
that,
when
n is
doubled,
the
error descreases
by a
factor
of
approximately
four.
Thus
find u G V
such
that
3.
(a)
This
BVP
models
a bar
whose
top end
(originally
at x = 0) is
free
and
whose
bottom
end is fixed at x = i. If we
apply
a
unit
force
to the
cross-section
at x = s,
then
the
part
of the bar
originally between
x = s and x = t
will
compress,
and the
part
of the bar
originally above
x = s
will
just
move rigidly
with
u(x)
—
u(s)
for 0
<
x < s. The
compression
of the
bottom
part
of the
bar
will satisfy Hooke's law:
Appendix
C.
Solutions
to
odd-numbered exercises 545
Section 5.6
1.
(b) Here are
the
errors for n = 10,20,40,80:
n
maximum error
10
1.6586 .
10
-0>
20
4.3226 .
10
-q
40
1.1036 .
10
-'l
80
2.7881.10
-0
We see
that,
when n is doubled,
the
error decreases by a factor of approximately
four.
Thus
error = 0
(~2
) .
3.
The
exact solution is u(x) =
x(l-
x
3
)/12. Here are
the
errors for n = 10,20,40,80:
n
maximum error
10
1.1286 .
10
-;j
20
2.9710 .
10
-'l
40
7.6186 . 10
-0
80
1.9288 .
10
-0
We
see
that,
when n is doubled,
the
error descreases by a factor of approximately
four. Thus
error = 0
(~2
) .
5.
The
weak form is
find
u E V such
that
1
£ {
du
dv
}
o k(x) dx (x)
dx
(x) +
p(x)u(x)v(x)
dx
=
1£
f(x)v(x)dx
for all v E
V.
The
bilinear form is
1
£ {
du
dv
}
a(u,v)=
0 k(X)dx(X)dx(X)+P(X)U(X)V(X) dx.
Section 5.7
1. u(x) =
xe-
x
.
3.
(a) This
BVP
models a
bar
whose
top
end
(originally
at
x = 0) is free
and
whose
bottom
end
is fixed
at
x =
£.
If
we
apply a unit force
to
the
cross-section
at
x =
s,
then
the
part
of
the
bar
originally between x = s
and
x = £ will
compress,
and
the
part
of
the
bar
originally above x = s will
just
move rigidly
with
u(x) = u(s) for 0
::;
x <
s.
The
compression of
the
bottom
part
of
the
bar
will satisfy Hooke's law:
k
u(x) 1
()
£ - x
--=
~ux
=--
i-x
k
Section
6.1
1.
The
steady-state
solution
of
Example
6.2
satisfies
the BVP
546
Appendix
C.
Solutions
to
odd-numbered
exercises
(the
uncompressed length
of the
part
of the bar
between
x = s and x = t is
i
—
x).
Therefore
we
obtain
The
Green's
function
is
(b)
The
Green's
function
is
(c) If
A;
is
constant, then
(d)
5.
By
direct integration,
we
obtain
the
following
solution
to
(5.67):
Since
x =
min{x,
i\
for x € [0,
£.],
we can
write
that
is,
7.
The
Green's
function
is
546
Appendix
C.
Solutions
to
odd-numbered exercises
(the
uncompressed length of
the
part
of
the
bar
between x = s
and
x = £ is
£ - x). Therefore we
obtain
u(x) = {
The
Green's function is
G(XjS) = {
i-s
k'
i-x
-k-'
i-s
-k-'
i-x
-k-'
0<
x < s,
s<x<£.
0<
x < s,
S < x <
e.
(b)
The
Green's function is
1
£ dz
G(Xj s) =
k(z)'
max{x,s}
(c)
If
k is constant,
then
(d)
G(XjS) =
e-ma;{x,s}
= {
l-s
k'
i-x
-k-'
0<
x < s,
S < x <
e.
u(X) =
In2
_!
_
X2
+
~
_In(l+x)
2 4 4 2
2'
5.
By
direct integration, we
obtain
the
following solution
to
(5.67):
r ds
u(x)
=p
10
k(s)'
Since x = min{x,
i}
for x E
[0,
il, we
can
write
_
{minix,s}
ds
U(X)
- p
10
k(s)'
that
is,
u(X) = g(Xje)p.
7.
The
Green's function is
~
2l
.
(n7rs)
.
(n7rx)
g(Xj
s) = L.J
kn
2
7r
2
sm
-e-
sm
-e-
.
n=l
Section 6.1
1.
The
steady-state
solution
of
Example 6.2 satisfies
the
BVP
-D::~
=
10-
7
,
0 < X < 100,
u(O)
=
0,
u(lOO)
=
O.
Appendix
C.
Solutions
to
odd-numbered
exercises
547
Either
by
solving
this
BVP or by
taking
the
limit
(as t
—>
oo)
of the
solution
of
Example 6.2,
we find
that
the
steady-state solution
is
3. The
solution
is
A
graph
of
u(-,
0.1)
is
given
in
Figure
C.10.
We
also have
Figure
C.10.
The
snapshot
w(-,0.1),
together
with
the
initial
temperature
distribution,
for
Exercise
6.1.3.
5.
With
Appendix
C.
Solutions
to
odd-numbered exercises
547
Either by solving this
BVP
or by taking
the
limit (as t
---+
00)
of
the
solution of
Example 6.2,
we
find
that
the
steady-state solution is
(
)
_~2.1O-3(1-(-1)n)
.
(n7rx)
Us
X -
~
Dn
3
7r
3
SIll
100
.
n=l
3.
The
solution is
00
2(_1)n+l
2 2
u(x,t)
=
'"'
e-
n
7r
tsin(n7rx).
~
n7r
n=l
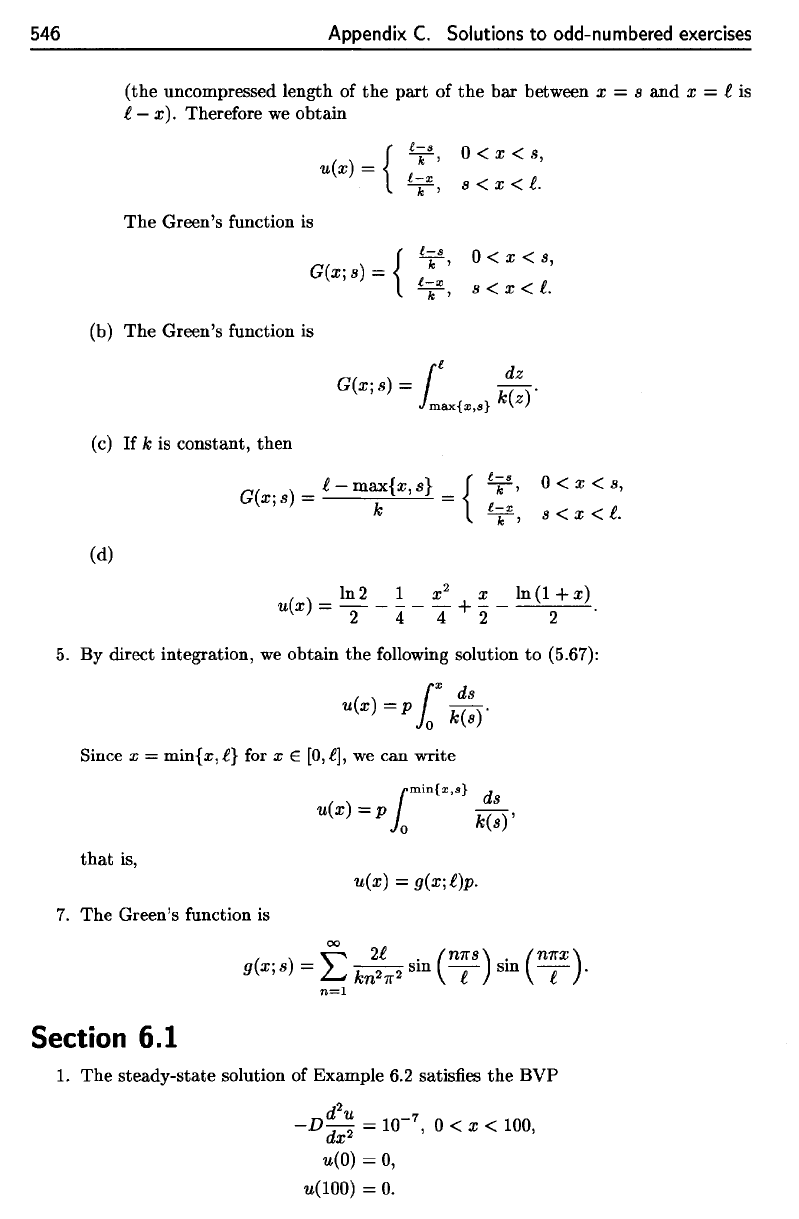
A graph of u(·, 0.1) is given in Figure C.lO.
1~====~~--~------~----~----~
0.9
0.8
0.7
0.6
0.5
0.4
0.3
0.2
0.1
u(·,O)
u(·,O.1 )
0.2
_.-.-,-,-,-,-
~.~
~.~
-'~,~
"'
..
...
...
,
0.4 0.6
0.8
x
Figure
C.1O. The snapshot u(·, 0.1), together with the initial temperature
distribution, for Exercise 6.1.3.
5.
With
x
p(x, t) = g(t) + C(h(t) - g(t))
and
v(x, t) = u(x, t) - p(x, t),
we
have
pcov
_",02
V
=pcou
_",02
U
_
(pc
OP
_",02
p
)
ot
ox
2
at
ox
2
ot
ox
2
=
f(x
t) -
pc
(d
9
(t)
+
~
(dh
(t) _
dg
(t)))
.
,
dt
"dt
dt
We also have
x
v(x, to) = u(x, to) - p(x, to) =
1j;(x)
- g(to) - C(h(to) - g(to))
