Gockenbach M.S. Partial Differential Equations. Analytical and Numerical Methods
Подождите немного. Документ загружается.


so 9
must
be one of the
values
bib
Appendix
C.
Solutions
to
odd-numbered
exercises
The
units
of / are
N/m
3
(force
per
unit
volume).
The
units
of the first
term
on the
left
are
and the
units
of the
second term
on the
left
are
7.
(a) We
have
while
Therefore,
(b)
Regardless
of the
value
of 0,
u(Q,
t)
=
0
holds
for all t. The
only
way
that
u(l,
t) — 0 can
hold
for all t is if
Section
2.3
1.
Units
of
acceleration (length
per
time squared).
3.
Units
of
velocity (length
per
time).
5.
The
internal
force
acting
on the end of the
string
at,
say,
x =
I,
is
If
this
end can
move
freely
in the
vertical direction,
force
balance implies
that
(C.I)
must
be
zero.
Section
3.1
1. A
function
of the
form
f(x)
= ax + b is
linear
if and
only
if b = 0.
Indeed,
if
/ : R
—»
R is
linear, then
f(x)
—
ax,
where
a =
/(I).
3. (a)
Vector space (subspace
of
C[0,1]).
(b)
Not a
vector space; does
not
contain
the
zero
function.
(Subset
of
C[0,1],
but
not
a
subspace.)
(c)
Vector space (subspace
of
C[Q,
1]).
(d)
Vector space.
(e)
Not a
vector space; does
not
contain
the
zero polynomial.
(Subsei
of
P
n
,
but
not a
sub
space.)
518
Appendix
C.
Solutions
to
odd-numbered exercises
The
units of 1 are
N/m
3
(force
per
unit volume).
The
units of
the
first
term
on
the
left are
kg m kgm/s2 N
m
3
S2
m
3
-
m
3
'
and
the
units of
the
second
term
on
the
left are
N 1 N
=
m
2
m m
3
·
7.
(a) We have
a
2
u 2 2
{)t2 (x, t) =
-c
()
u(x, t),
while
a
2
u 2
ax2 (x, t) =
-f}
u(x,
t).
Therefore,
a
2
u 2 a
2
u 2 2 2 2
{)t2 - C
ax
2
=
-c
f}
u + c
()
u =
o.
(b) Regardless of
the
value of f},
u(O,
t) = 0 holds for all t.
The
only way
that
u(l,
t)
= 0 can hold for all t is if
sin
«(}l)
=
0,
so
f}
must be one of
the
values
()
=
~7r,
n =
0,
±1, ±2,
....
Section 2.3
1. Units of acceleration (length
per
time
squared).
3.
Units of velocity (length
per
time).
5.
The
internal force acting
on
the
end
of
the
string at, say, x =
l,
is
au
T
ax
(l, t).
(C.1)
If
this end can move freely in
the
vertical direction, force balance implies
that
(C.1)
must
be zero.
Section 3.1
1. A function of
the
form
I(x)
=
ax
+ b is linear if
and
only if b =
O.
Indeed, if
I:
R
-t
R is linear,
then
I(x)
= ax, where a = 1(1).
3.
(a) Vector space (subspace of
e[O,
1)).
(b) Not a vector space; does not contain
the
zero function. (Subset of
e[O,
1],
but
not
a subspace.)
(c) Vector space (subspace of
e[O,
1]).
(d) Vector space.
(e) Not a vector space; does not contain
the
zero polynomial. (Subset of P
n
,
but
not
a subspace.)

Appendix
C.
Solutions
to
odd-numbered
exercises
519
5.
Suppose
u
€
C
l
[a,b]
is any
nonzero
function.
Then
while
Since
L(1u)
^
2Lu,
L is not
linear.
7.
(a) The
proof
is a
direct calculation:
and
Now,
as
desired.
The
third equality
follows
from
the
commutative
and
associative
properties
of
addition, while
the
fourth
equality
follows
from
the
distributive
property
of
multiplication over addition.
Appendix
C.
Solutions
to odd-numbered
exercises
5.
Suppose u E C
1
[a,
b]
is any nonzero function.
Then
du
3
du
3
L(2u) = 2
dx
+ (2u) = 2 dx + 8u ,
while
du
3
2Lu
= 2 dx + 2u .
Since L(2u)
=1=
2Lu, L is not linear.
7.
(a)
The
proof is a direct calculation:
A(ax
+
,Bz)
=
=
[:~~
:~~]
[
~:~!
~~~
]
[
all
(axl
+
,BZl)
+ a12(ax2 +
,BZ2)
]
a21(axl
+ ,Bzl) +
a22(
ax
2 +
,Bz2)
[
a(allxl
+ a12x2) + ,B(allzl + a12z2) ]
a(a21xl
+ a22x2) +
,B(a21z1
+ a22z2)
= a [
allXl
+
a12X2
] +,B [
allZl
+
a12Z2
]
a21Xl
+
a22X2
a21Z1
+
a22Z2
=
aAx+,BAz.
This shows
that
the
operator defined by A is linear.
(b) We have
and
Now,
n
(A(ax+,BY))i =
La;j(axj
+,BYj)
j=l
n
(aAx
+ ,BAY)i = a L aijXj +,B L a;jYj·
j=l j=l
n
(A(ax+,By));
=
Laij(aXj
+,BYj)
j=l
n
= L (aaijXj + ,BaijYj)
j=l
n n
=
Laaijxj
+
L,BaijYj
j=l j=l
n n
= a L aijXj +
,B
L aijYj
j=l
j=l
= (a
Ax
+ ,BAy);,
519
as desired.
The
third
equality follows from
the
commutative
and
associative
properties of addition, while
the
fourth equality follows from
the
distributive
property of multiplication over addition.
520
Appendix
C.
Solutions
to
odd-numbered
exercises
Section
3.2
1.
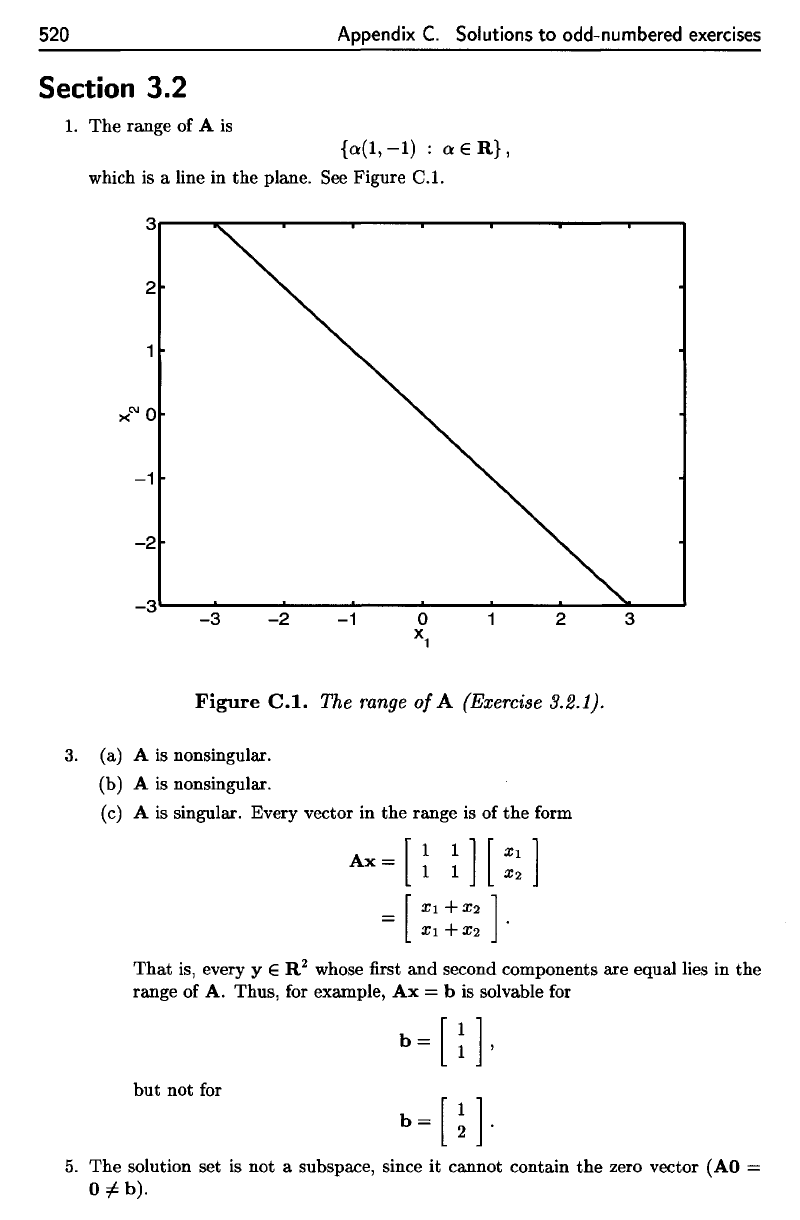
The
range
of A is
{a(l,-l)
:
a€R},
which
is a
line
in the
plane.
See
Figure
C.I.
Figure
C.I.
The
range
of
A
(Exercise
3.2.1).
3.
(a) A is
nonsingular.
(b)
A is
nonsingular.
(c)
A is
singular. Every vector
in the
range
is of the
form
That
is,
every
y € R
2
whose
first and
second components
are
equal lies
in the
range
of A.
Thus,
for
example,
Ax = b is
solvable
for
but not for
5.
The
solution
set is not a
subspace,
since
it
cannot contain
the
zero vector
(AO
=
O^b).
520
Appendix
C.
Solutions
to
odd-numbered exercises
Section 3.2
1.
The
range of A is
{o:(l,-l)
:
O:ER},
which is a line in
the
plane. See Figure
C.l.
3~--~----~----r---~~--~----~-----r--~
2
)(N
0
-1
-2
-3~--~----~----~--~~--~----~----~--~
-3 -2
-1
0 2 3
Xl
Figure
C.l.
The range
of
A (Exercise 3.2.1).
3.
(a) A is nonsingular.
(b) A is nonsingular.
(c) A is singular. Every vector in
the
range is of
the
form
Ax
=
[~
~]
[
::
]
= [
~~!~:
] .
That
is, every y E R
2
whose first
and
second components are equal lies in
the
range of
A.
Thus, for example,
Ax
= b is solvable for
but
not for
b=[~],
b=[;].
5.
The
solution set is not a subspace, since
it
cannot contain
the
zero vector (AO =
o
i=
b).

The
last
step
follows
from
the
Neumann condition
at x
=
a. We now
integrate
again:
Integrating once yields,
by the
fundamental theorem
of
calculus,
Appendix
C.
Solutions
to
odd-numbered
exercises
521
7.
The
null space
of
L
is the set of all first-degree
polynomials:
9.
(a) The
only functions
in
C
2
[a,
6]
that
satisfy
are
functions
of the
form
u(x)
=
Cix
+
C?.
The
Neumann boundary condition
at the
left
endpoint implies
that
C\ = 0, and the
Dirichlet boundary condition
at the
right endpoint implies
that
€2
= 0.
Therefore, only
the
zero
function
is
a
solution
to
L^u
= 0, and so the
null space
of
Z/m
is
trivial.
(b)
Suppose
/
G
C[a,6]
is
given
and u €
C^[a,
b]
satisfies
This
shows
that
L/mU
= f has a
unique solution
for
each
/ €
C[a,
b].
11. By the
fundamental theorem
of
calculus,
satisfies
Du =
f.
However,
this
solution
is not
unique;
for any
constant
(7,
is
another solution.
Appendix
C.
Solutions
to
odd-numbered exercises
7.
The
null space
of
L is
the
set of all first-degree polynomials:
N(L)
=
{u:
[a,b]-+ R : u(x) =
mx
+ c for some
m,c
E
R}.
9.
(a)
The
only functions in
CZ[a,
b]
that
satisfy
dZu
--=0
dx
z
521
are functions of
the
form u(x) = C1x + C
z
.
The
Neumann boundary condition
at
the
left endpoint implies
that
Cl =
0,
and
the
Dirichlet boundary condition
at
the
right endpoint implies
that
C2
=
O.
Therefore, only
the
zero function
is
a solution
to
Lin u = 0,
and
so
the
null space of Lin is trivial.
(b) Suppose
f E C[a,
b]
is given
and
u E
C~
[a,
b]
satisfies
d
2
u
- dx
2
(x) =
f(x),
a < x <
b.
Integrating once yields, by
the
fundamental theorem of calculus,
r
d2
r
-
ia
dx~
(s) ds =
ia
f(s)
ds
du du
(X
=>
- dx (x) + dx
(a)
=
ia
f(s)
ds
d r
=>
d:(x)
= -
ia
f(s)ds.
The
last step follows from
the
Neumann condition
at
x = a. We now integrate
again:
d r
d:
(x) = -
ia
f(s)
ds
l
b
d
Ib
r
=>
X
d:(z)dz
= - x
ia
f(s)dsdz
=>
u(b) - u(x) =
-lb
1
z
f(s)
ds dz
=>
u(x)
= i
a
1
Z
f(s)dsdz.
This shows
that
Linu
= f has a unique solution for each f E
C[a,
b].
11. By
the
fundamental theorem of calculus,
u(x)
=
IX
f(s)ds
satisfies
Du
= f. However, this solution is
not
unique; for any constant
C,
u(x) =
IX
f(s)
ds + C
is another solution.

522
Appendix
C.
Solutions
to
odd-numbered
exercises
Section
3.3
1.
(a)
Both equal
(14,4,
-5).
(b)
Both equal
3.
The
given
set is not a
basis.
If A is the
matrix whose columns
are the
given vectors,
then
A/"(A)
is not
trivial.
5.
We
know
that
P%
has
dimension
3, and
therefore
it
suffices
to
show either
that
the
given
set of
three vectors spans
Ti
or
that
it is
linearly independent.
If
p
e
Pz,
then
we
write
and
define
the
polynomial
Then
and, similarly,
q(x-z)
=
p(xz),
q(xz)
=
p(%s)-
But
then
p and q are
second-
degree polynomials
that
agree
at
three distinct points,
and
three points determine
a
quadratic
(just
as two
points determine
a
line). Therefore,
and we
have shown
that
every
p €
Pi
can be
written
as a
linear combination
of
LI,
1/2,£3.
This completes
the
proof.
Section
3.4
1. (a) The
verification
is a
direct calculation
of
Vi
•
Vj
for the 6
combinations
of
i,
j.
For
example,
and so
forth,
(b)
522
Appendix
C.
Solutions
to
odd-numbered exercises
Section 3.3
1. (a)
Both
equal (14,4,
-5).
(b) Both equal
2:7=1
(Vj)iXj.
3.
The
given set is
not
a basis.
If
A is
the
matrix
whose columns are
the
given vectors,
then
N(A)
is not trivial.
5.
We know
that
P2
has dimension
3,
and
therefore
it
suffices
to
show either
that
the
given set
of
three vectors spans
P2
or
that
it
is linearly independent.
If
p E
P2,
then
we write
Cl
= p(Xl), C3 = P(X3), C3 = p(X3)
and
define
the
polynomial
Then
and, similarly, q(X2) = p(X2), q(X3) = p(X3)'
But
then
p
and
q are second-
degree polynomials
that
agree
at
three
distinct points,
and
three points determine
a quadratic (just as two points determine a line). Therefore,
and
we
have shown
that
every p E
P2
can
be written as a linear combination of
L
1
,
L
2
,
L
3
•
This completes
the
proof.
Section 3.4
1. (a)
The
verification is a direct calculation of
Vi
•
Vj
for
the
6 combinations of i,
j.
For example,
1 1 1 1 1 1
Vl'Vl=--+--+--
V3 V3
V3
V3 V3
V3
111
=
3"
+
3"
+
3"
= 1,
Vl'V2
=
~ ~
+
~O
+
~
( -
~)
1 1
=
v'6
-
v'6
=
0,
and
so forth.
(b)
x =
(VI'
X)Vl
+
(V2
.
X)V2
+
(V3
.
X)V3
=
~
VI
+
OV2
+ ( -
~)
V3.

or
See
Figure C.3.
Appendix
C.
Solutions
to
odd-numbered
exercises
523
3. We
have
Therefore,
if
and
only
if (x, y) = 0.
5.
First
of
all,
if
then since
vn
e
W for
each
i,
we
have,
in
particular,
Suppose,
on the
other hand,
that
If
z is any
vector
in
W,
then, since
{wi,
W2,...,
w
n
}
is a
basis
for
W',
there exist
scalars
ai,
0:2,
• •
•,
ot
n
such
that
We
then have
This completes
the
proof.
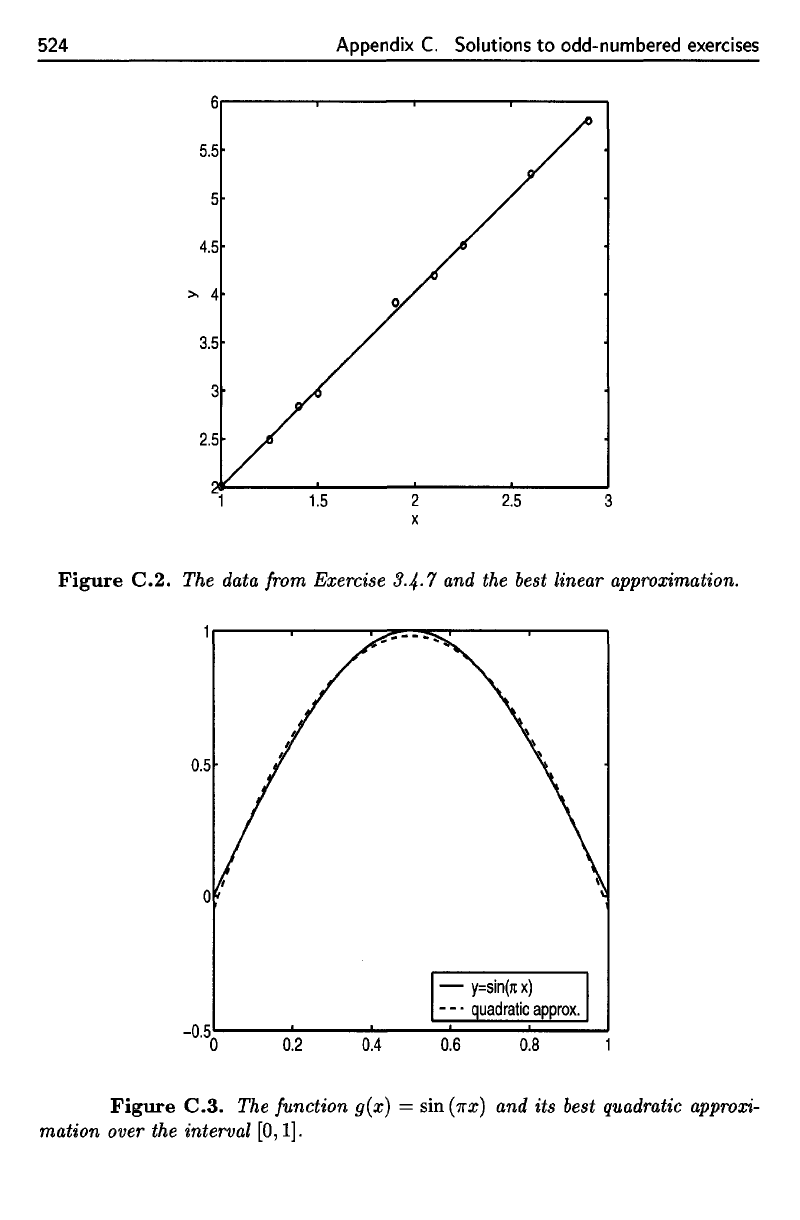
7.
The
best
approximation
to the
given
data
is y —
2.0111x
—
0.0018984.
See
Figure
C.2.
9. The
projection
of g
onto
7*2
is
Appendix
C.
Solutions
to
odd-numbered exercises
3. We have
Ilx+yl12 =
(x+y,x+y)
Therefore,
if
and
only
if
(x,y)
=
O.
5.
First
of all, if
= (x, x + y) + (y, x + y)
=
(x,x)
+
(x,y)
+
(y,x)
+
(y,y)
=
(x,x)
+
2(x,y)
+
(y,y)
=
IIxll
2
+
2(x,y)
+
Ilyll2.
(y, z) = 0 for all z E
W,
then
since
Wi
E W for each i, we have, in particular,
(y,
Wi)
= 0, i = 1,2,
...
, n.
Suppose, on
the
other
hand,
that
(y,
Wi)
= 0, i = 1,2,
...
,n.
523
If
z is any vector in
W,
then, since
{Wi,
W2,
...
, w
n
}
is a basis for
W,
there
exist
scalars
ai,
a2,
...
,an
such
that
We
then
have
n
Z =
Laiwi.
i=l
n
=
Lai
(y,Wi)
i=l
i=l
=0.
This
completes
the
proof.
7.
The
best
approximation
to
the
given
data
is y = 2.0111x - 0.0018984. See Figure
C.2.
9.
The
projection
of
9 onto P2 is
2
2V5(7r
2
-
12)
-Ql(X) +
OQ2(X)
+ 3
Q3(X)
7r
7r
or
See Figure C.3.
524
Appendix
C.
Solutions
to
odd-numbered exercises
Figure
C.3.
The
function
g(x]
= sin
(TTX)
and its
best
quadratic
approxi-
mation
over
the
interval
[0,1].
Figure
C.2.
The
data from Exercise
3-4-7
and the
best linear approximation.
524
Appendix
C.
Solutions
to
odd-numbered
exercises
Figure
C.2.
The data from Exercise 3.4.7 and the best linear approximation.
Figure
C.3.
The function g(x) = sin
(1fx)
and its best quadratic approxi-
mation over the interval
[0,1].

Appendix
C.
Solutions
to
odd-numbered
exercises
525
3. The
eigenvalues
and
eigenvectors
of A are
AI
= 2, A2 = 1,
AS
=
—1
and
5.
The
computation
of
u^
•
b/Aj
costs
2n
operations,
so
computing
all
n
of
these
ra-
tios
costs
2n
2
operations. Computing
the
linear combination
is
then equivalent
to
another
n dot
products,
so the
total
cost
is
Thus
(b)
The
eigenvalues
\j are all
positive
and are
increasing with
the
frequency
j.
Section
3.5
1.
The
eigenvalues
of A are
AI
= 200 and
A2
=
100,
and the
corresponding (normalized)
eigenvectors
are
respectively.
The
solution
is
The
solution
of the Ax
=
b is
7.
(a) For k =
2,3,...,
n
—
1, we
have
Similar calculations show
that
this
formula
holds
for k =
I
and k
=
n
also.
Therefore,
s^'
is an
eigenvector
of L
with eigenvalue
Appendix
C.
Solutions
to
odd-numbered exercises
525
Section 3.5
1.
The
eigenvalues of A are >'1 = 200
and
>'2 = 100,
and
the
corresponding (normalized)
eigenvectors are
[
-0.8
] [ 0.6 ]
U1
=
0.6'
U2
= 0.8 '
respectively.
The
solution is
b .
U1
b .
U2
[ 1 ]
X=~U1+~U2=
1 .
3.
The
eigenvalues
and
eigenvectors of A are >'1 =
2,
>'2 = 1,
>'3
=
-1
and
The
solution of
the
Ax
= b is
[
-3/2]
1/2
.
5/2
5.
The
computation
of
Ui
. b/>.; costs 2n operations,
so
computing all n of these ra-
tios costs
2n2 operations. Computing
the
linear combination is
then
equivalent
to
another n dot products,
so
the
total
cost is
2n
2
+ n * (2n
-1)
=
4n
2
-
n = O(4n
2
).
7.
(a) For k = 2,3,
...
,n
-1,
we
have
(Ls(j))
k =
;2
(-
sin ((k - l)j7rh) + 2 sin (kj7rh) - sin ((k + l)j7rh))
Thus
=
;2
(-
sin (kj7rh) cos (j7rh) + cos (kj7rh) sin (j7rh) + 2 sin (kj7rh)
- sin (kj7rh) cos (j7rh) - cos (kj7rh) sin (j7rh))
=
;2
(2
- 2 cos (j7rh)) sin (kj7rh)
=
;2
(2-2cos(j7rh))s~).
(Ls(j))
k =
;2
(2
- 2 cos (j7rh))
s~),
k = 2,3,
...
, n -
l.
Similar calculations show
that
this formula holds for k = 1
and
k = n also.
Therefore, s(j) is an eigenvector of L with eigenvalue
\.
_ 2 - 2 cos (j7rh)
AJ
- h
2
•
(b)
The
eigenvalues
>.j
are all positive
and
are increasing with
the
frequency
j.
526
Appendix
C.
Solutions
to
odd-numbered
exercises
(c)
The
right-hand side
b can be
expressed
as
while
the
solution
x of Lx = b is
Since
Xj
increases with
j,
this shows
that,
in
producing
x, the
higher frequency
components
of b are
dampened more than
are the
lower
frequency
components
of
b.
Thus
x is
smoother than
b.
Section
4.1
1.
Define
Then
3.
Define
Then
5.
Define
Then
the first-order
system
is
526
Appendix
C.
Solutions
to
odd-numbered exercises
(c)
The
right-hand side b can
be
expressed as
b =
(8{1)
.
b)
8(1)
+
(8(2).
b)
8(2)
+ ... +
(8(n).
b)
8(n),
while
the
solution x
of
Lx
= b is
8(1)
. x
(1)
8(2)
. x
(2)
8(n)
. X
(n)
X =
---8
+
---8
+ ... +
---8
Al
A2
An
Since
Aj
increases with
j,
this
shows
that,
in producing
x,
the
higher frequency
components of
b are
dampened
more
than
are
the
lower frequency components
of
b.
Thus
x is smoother
than
b.
Section 4.1
1. Define
Then
3.
Define
Then
5.
Define
du
Xl
=
U,
X2
=
dt'
dXl
dXl
dt
=X2,
dX2
1
dt
=
-2"
X
l.
dt
=X2,
dX2
--a.:;:=X3,
dX3
--a.:;:=X4,
dX4
2 .
Tt
=
X3
-
Xl
+ sm
t.
dp dq
Xl
= p,
X2
=
dt'
X3
=
q,
X4
=
dt'
Then
the
first-order system is
dXl
Tt
=X2,
dX2
mITt
=
/!(Xl,X3,X2,X4),
dX3
dt
=X4,
dX4
m2Tt
=
h(Xl,X3,X2,X4).

Appendix
C.
Solutions
to
odd-numbered
exercises
527
Section
4.2
1. (a) We first
note
that
the
zero function
is a
solution
of
(4.4),
so S is
nonempty.
If
u,
v € S and a,
/3
G
R,
then
w
=
au
+
/3v
satisfies
Thus
w is
also
a
solution
of
(4.4),
which shows
that
S is a
subspace.
(b)
As
explained
in the
text,
no
matter
what
the
values
of
a,
6,
c (a
^
0), the
solution space
is
spanned
by two
functions. Thus
S is finite-dimensional and
it has
dimension
at
most
2.
Moreover,
it is
easy
to see
that
each
of the
sets
{e
rit
,e
r2
*}
(n
/
r
2
),
{e"*
cos
(A*),
e
M
*
sin
(At)},
and
{e
r
\te
rt
}
is
linearly
in-
dependent, since
a set of two
functions
is
linearly dependent
if and
only
if one
of
the
functions
is a
multiple
of the
other. Thus,
in
every case,
S has a
basis
with
two
functions,
and so S is
two-dimensional.
3.
Suppose
that
the
characteristic polynomial
of
(4.4)
has a
single,
repeated
root
r =
—6/(2a)
(so
6
2
—
4ac
= 0).
Then,
as
shown
in the
text,
is a
solution
of
(4.4)
for
each choice
of
ci,
02-
We
wish
to
show
that,
given
fci,
ki
€ R,
there
is a
unique choice
of
ci,
ci
such
that
-u(O)
=
ki,
du/dt(0)
=
k^.
We
have
Therefore,
the
equations
•u(O)
=
ki,
du/dt(0)
—
k<2
simplify
to
Since
the
coefficient
matrix
is
obviously
nonsingular
(regardless
of the
value
of
r),
there
is a
unique solution
Ci,C2
for
each
ki,kz.
5.
(a) The
only solution
is
u(x)
=
0.
(b)
The
only solution
is
u(x)
=
0.
(c)
The
function
u(x)
= sin
(-KX)
is a
nonzero solution.
It is not
unique, since
any
multiple
of it is
another solution.
7.
By the
product rule
and the
fundamental theorem
of
calculus,
Appendix
C.
Solutions
to
odd-numbered exercises 527
Section 4.2
1.
(a) We first
note
that
the
zero function is a solution of (4.4), so
Sis
nonempty.
If
u, v E S
and
a,
fJ
E
R,
then
w =
au
+
fJv
satisfies
d
2
w
dw
d
2
d
a dt
2
+
bdt
+ cw = a dt
2
[au +
fJv]
+ b dt
[au
+
fJv]
+ c(au +
fJv)
= a ( a
~::
+
fJ
~:~)
+ b ( a
~~
+
fJ
~:)
+ c(
au
+
fJv)
= a
(a
~::
+ b
~~
+
cu)
+
fJ
(a
~:~
+ b
~:
+
cv)
= a . 0 +
fJ
. 0 =
O.
Thus
w is also a solution of (4.4), which shows
that
S is a subspace.
(b) As explained in
the
text,
no
matter
what
the
values of a,
b,
c (a
::j:.
0),
the
solution space is
spanned
by two functions.
Thus
S is finite-dimensional
and
it
has dimension
at
most
2.
Moreover,
it
is easy
to
see
that
each
of
the
sets
{eTlt,eT2t} (rl::j:. r2),
{el£t
cos (At),el£tsin(At)},
and
{eTt,te
rt
}
is
linearly in-
dependent, since a set
of
two functions is linearly
dependent
if
and
only if one
of
the
functions is a multiple
of
the
other. Thus,
in
every case, S has a basis
with
two functions,
and
so S is two-dimensional.
3. Suppose
that
the
characteristic polynomial of (4.4) has a single,
repeated
root r =
-b/(2a)
(so b
2
-
4ac = 0). Then, as shown in
the
text,
u(t) = Clert + c2te
Tt
is a solution
of
(4.4) for each choice of Cl,
C2.
We wish
to
show
that,
given
kl,
k2
E
R,
there
is a unique choice
of
CI,
C2
such
that
u(O)
=
kl,
du/dt(O) =
k2.
We have
du ( )
Tt
Tt Tt
dt t = rCle +
C2e
+
rC2te
.
Therefore,
the
equations
u(O)
=
kl'
du/dt(O) =
k2
simplify
to
[;
~]
C =
k.
Since
the
coefficient
matrix
is obviously nonsingular (regardless
of
the
value of
r),
there
is a unique solution
CI,
C2 for each
kl,
k
2
•
5. (a)
The
only solution is
u(x)
=
O.
(b)
The
only solution is
u(
x)
=
O.
(c)
The
function
u(
x)
= sin
(7rx)
is a nonzero solution.
It
is
not
unique, since any
multiple
of
it is
another
solution.
7.
By
the
product
rule
and
the
fundamental theorem
of
calculus,
:t
[1:
ea(t-S)f(S)dS] =
:t
[eat
1:
e-asf(S)dS]
=
ae
at
it
e -as f(s) ds + eate-
at
f(t)
to
= a
it
ea(t-s)
f(s)
ds
+ J(t).
to
