Gockenbach M.S. Partial Differential Equations. Analytical and Numerical Methods

498

Chapter

10.

More about

finite

element methods

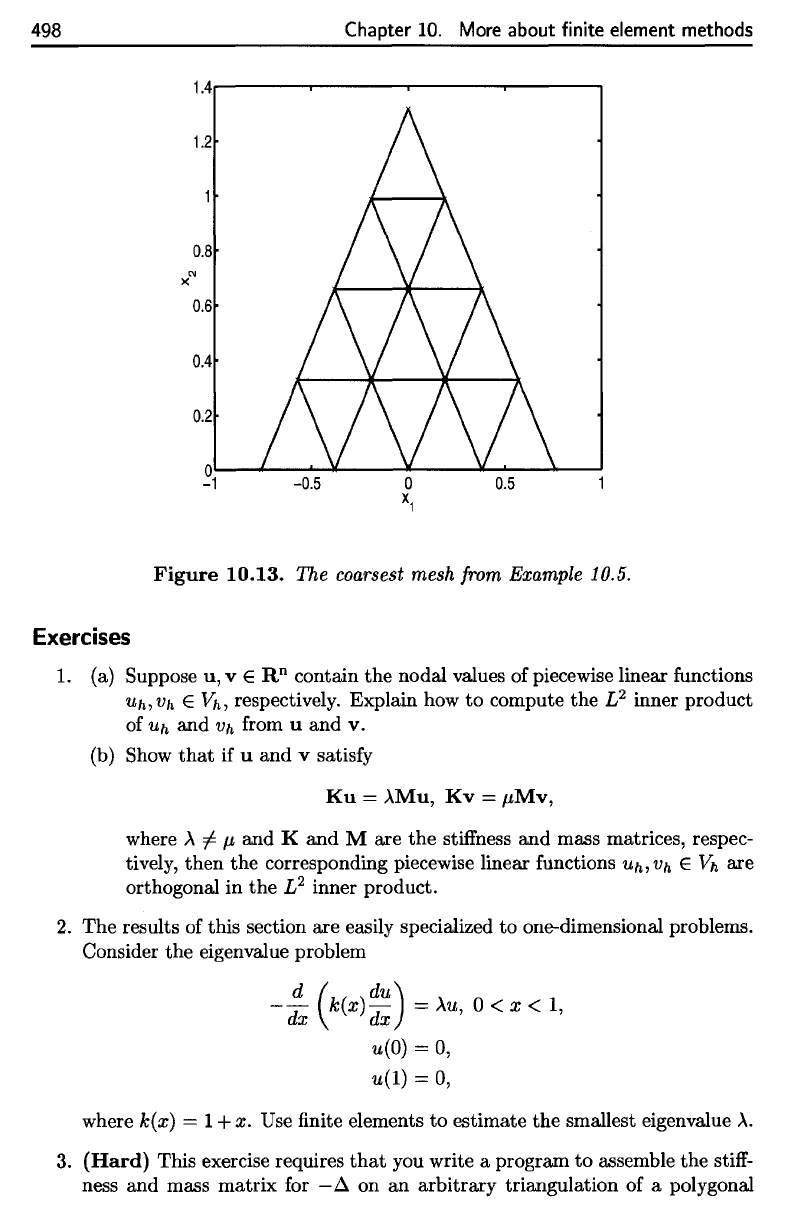
Figure

10.13.

The

coarsest

mesh

from

Example

10.5.

Exercises

1.

(a)

Suppose

u, v

e

R

n

contain

the

nodal values

of

piecewise linear

functions

Uh,Vh

€ Vh,

respectively. Explain

how to

compute

the L

2

inner product

of

Uh

and Vh

from

u

and v.

(b)

Show

that

if u and v

satisfy

where

A

/

//

and K and M are the

stiffness

and

mass matrices, respec-

tively, then

the

corresponding piecewise linear functions

Uh,Vh

€

Vh are

orthogonal

in the

I/

2

inner product.

2.

The

results

of

this section

are

easily specialized

to

one-dimensional problems.

Consider

the

eigenvalue problem

where

k(x]

= 1 + x. Use finite

elements

to

estimate

the

smallest eigenvalue

A.

3.

(Hard) This exercise requires

that

you

write

a

program

to

assemble

the

stiff-

ness

and

mass matrix

for

—A

on an

arbitrary

triangulation

of a

polygonal

498

Chapter 10. More about finite element methods

1.4.-------,------r-----.----.....,

1.2

0.8

'"

x

0.6

0.4

0.2

0

-1

-0.5

0

0.5

x

1

Figure

10.13.

The coarsest mesh from Example 10.5.

Exercises

1. (a) Suppose

u,

v

ERn

contain

the

nodal values of piecewise linear functions

Uh,

Vh

E

Vh,

respectively. Explain how

to

compute

the

L2

inner product

of

Uh

and

Vh

from u

and

v.

(b) Show

that

if u

and

v satisfy

Ku

=

AMu,

Kv

= p,Mv,

where A

=I-

JL

and

K

and

M are

the

stiffness

and

mass matrices, respec-

tively,

then

the

corresponding piecewise linear functions

Uh,

Vh

E

Vh

are

orthogonal in

the

L2

inner product.

2.

The

results of this section are easily specialized

to

one-dimensional problems.

Consider

the

eigenvalue problem

d (

dU)

-

dx

k(x)

dx

=

AU,

0 < x <

1,

u(O)

= 0,

u(1)

= 0,

where k(x) = 1 + x. Use finite elements

to

estimate

the

smallest eigenvalue

A.

3. (Hard) This exercise requires

that

you write a program

to

assemble

the

stiff-

ness

and

mass

matrix

for -..6. on

an

arbitrary

triangulation of a polygonal

10.5. Suggestions

for

further reading

An

excellent introduction

to the

theory

of

finite

element methods

is the

book

by

Brenner

and

Scott

[6]

mentioned earlier. Strang

and Fix

[45] also discusses

the

con-

vergence theory

for finite

elements applied

to

time-dependent PDEs

and

eigenvalue

problems.

Most

finite

element

references

discuss

the

computer implementation

of finite

elements

in

only general terms. Readers

wishing

to

learn more

about

this

issue

can

consult

the

Texas

Finite Element Series

[3] and

Kwon

and

Bang

[32].

As

mentioned early

in

this chapter, mesh generation

is an

important

area

of

study

in its own

right;

it is

treated

by

Knupp

and

Steinberg

[31].

10.5. Suggestions for further reading

499

domain

D.

You

will also need access to a routine

to

solve the generalized

eigenvalue problem.

(a) Repeat Example 10.5, replacing the triangular domain by a domain

bounded by a regular pentagon with area

1.

(b) Let

A~n)

be the smallest eigenvalue of

-~

on a region having area 1 and

bounded by a regular n-gon. Form a conjecture about

1

·

dn)

1m

Al

.

n-+oo

(c)

Test your hypothesis by repeating Example 10.5 for a regular n-gon,

choosing n

to

be the largest integer

that

is

practical. (Whatever value of

n you choose, you have

to

create one or more meshes on

the

corresponding

n-gon.)

4.

Repeat Exercise 2 using k(x) = 1 + (x _1)2.

10.5 Suggestions for further reading

An excellent introduction

to

the theory of finite element methods

is

the book by

Brenner and Scott

[6]

mentioned earlier. Strang and Fix

[45]

also discusses the con-

vergence theory

for

finite elements applied

to

time-dependent PDEs and eigenvalue

problems.

Most finite element references discuss the computer implementation of finite

elements in only general terms. Readers wishing

to

learn more about this issue can

consult the

Texas

Finite Element Series

[3]

and Kwon and Bang

[32].

As

mentioned early in this chapter, mesh generation

is

an

important area of

study in its own right; it

is

treated by Knupp and Steinberg

[31].

This page intentionally left blank

Appendix

A

Theorem

A.I.

Let A 6

R

nxn

be

symmetric,

and

suppose

A has an

eigenvalue

X

of

(algebraic)

multiplicity

k

(meaning

that

A is a

root

of

multiplicity

k of the

characteristic

polynomial

of

A).

Then

A has k

linearly

independent

eigenvectors

corresponding

to A.

Proof.

We

argue

by

induction

on n. The

result holds trivially

for

n

= 1. We

assume

it

holds

for

symmetric

(n

—

1) x (n

—

1)

matrices,

and

suppose

A

e

R

nxn

is

symmetric

and has an

eigenvalue

A of

(algebraic) multiplicity

k.

There

exists

xi

^

0

such

that

Axi

=

Axi.

We can

assume

that

||xi||

= 1

(since

Xi/||xi||

is

also

an

eigenvector

of A), and we

extend

xi

to an

orthonormal basis

{xi,x

2

,...

,x

n

}.

Then

where

X

e

R

nxn

is

defined

by X =

[xi|x

2

|

• • •

|x

n

].

We

have

and

501

Theorem

3.47

Proof of

of Theorem 3.47

Theorem

A.I.

Let

A E

Rnxn

be

symmetric, and suppose A has an eigenvalue

A

of

(algebraic) multiplicity k (meaning that A is a root

of

multiplicity k

of

the

characteristic polynomial

of

A). Then A has k linearly independent eigenvectors

corresponding to

A.

Proof.

We

argue by induction on

n.

The

result holds trivially for n =

1.

We

assume it holds for symmetric (n -

1)

x (n -

1)

matrices,

and

suppose A E

Rnxn

is

symmetric and has

an

eigenvalue A of (algebraic) multiplicity

k.

There exists

Xl

::f-

0 such

that

AXl =

AXl.

We

can assume

that

Ilxlll = 1 (since

xdlixlil

is

also

an

eigenvector of

A),

and

we

extend

Xl

to

an

orthonormal basis

{Xl,X2,

•..

,X

n

}.

Then

[

Xl

Ax,

xf

Ax

2

x[Axn

1

xfAxl

xf

Ax

2

xfAxn

XTAX=

.

. ,

X;AXl

X;AX2

x;Axn

where X E

Rnxn

is defined by X = [xllx21··

·Ix

n

].

We

have

and

xi

AXi =

(AXlf

Xi

(since A

is

symmetric)

= Axi

Xi

=

AJ

il

.

501

502

Appendix

A.

Proof

of

Theorem 3.47

(The symbol

<%

is 1 if i = j and 0 if i

^

j.)

Therefore,

The

matrix

B is

symmetric. Also,

where

B

<E

RCn-

1

)*^-

1

)

[

s

defined

by

since

X

T

=

X"

1

and

therefore

det

(X

T

)

= det (X)

l

.

It

follows

that

Since

A is an

eigenvalue

of A of

multiplicity

Ar,

it

must

be an

eigenvalue

of B of

multiplicity

k -

1,

and

therefore,

by the

induction hypothesis,

B has k

—

1

linearly

independent eigenvectors

y2,ys,

• • • ,

yfc

corresponding

to A. We

define

for

i =

2,3,...,

k, and

define

Uj

=

XyV

Then

502

Appendix

A.

Proof of Theorem 3.47

(The symbol 8ij

is

1 if i = j

and

0

if

i

¥-

j.)

Therefore,

[

~

xI

~X2

XTAX=

0:

X;AX2

o 1

xIAxn

:::

x

T

lx

n n

=[~

~],

where

BE

R(n-1)x(n-1)

is defined by

The matrix B

is

symmetric. Also,

det

(..xl

-

XT

AX) = det

(XT

(..xl

- A)X)

= det (XT) det

(..xl

- A) det (X)

= det

(..xl

- A),

since X

T

=

X-

1

and therefore det (XT) = det (X)

-1.

It

follows

that

l

..x-..x 0 I

det

(..xl

- A) = 0

..xl

_ B

=

(..x

-..x) det (,\1 -

B).

Since ,\

is

an

eigenvalue of A of multiplicity k, it must be an eigenvalue of B of

multiplicity

k -

1,

and therefore, by the induction hypothesis, B has k - 1 linearly

independent eigenvectors

Y2,

Y3,

...

,Yk

corresponding

to

A.

We

define

for

i = 2,3,

...

, k,

and

define

Ui

=

XYi'

Then

AUi

= X [

~

= X [

~

Appendix

A.

Proof

of

Theorem

3.47

503

(the columns

of X are

orthonormal,

so

X

T

X

= I;

this

is why the

factor

of

X

T

X

dis-

appeared

in the

above

calculation).

This shows

that

u

2

,113,...,

u/t

are

eigenvectors

of

A

corresponding

to A.

Moreover,

(0

is the

zero vector

in

R

n

1

],

from

which

we can

deduce

that

{ui,

112,...,

u^}

is

a

linearly independent

set of

eigenvectors

of A

corresponding

to A.

This completes

the

proof.

Appendix

A.

Proof

of

Theorem 3.47

503

(the columns of X are orthonormal, so

XTX

= I; this

is

why

the

factor of

XTX

dis-

appeared in the above calculation). This shows

that

U2, U3,

...

,

Uk

are eigenvectors

of A corresponding to

>..

Moreover,

(0

is

the zero vector in

Rn-l),

from which

we

can deduce

that

{Ul,U2,

...

,Uk}

is

a linearly independent set of eigenvectors of A corresponding

to

>..

This completes

the

proof. D

This page intentionally left blank

Appendix

B

the

data

in two

B.O.I

Inhomogeneous

Dirichlet

conditions

on a

rectangle

The

method

of

shifting

the

data

can be

used

to

transform

an

inhomogeneous Dirich-

let

problem

to a

homogeneous Dirichlet problem. This technique works just

as it

did

for a

one-dimensional problem, although

in two

dimensions

it is

more

difficult

to find a

function satisfying

the

boundary conditions.

We

consider

the BVP

where

Q,

is the

rectangle defined

in

(8.10)

and

dtt

=

TI

U

T

2

U

T

3

U

T

4

,

as in

(8.13).

We

will assume

that

the

boundary

data

are

continuous,

so

Suppose

we find a

function

p

defined

on

J7

and

satisfying

p(x)

=

#(x)

for all

x

e

dfL

We

then

define

v = u

—

p and

note

that

and

(since

p

satisfies

the

same Dirichlet conditions

that

u is to

satisfy).

We can

then

solve

where

RDR

Shifting

dmensions

Appendix B

eng

the

data

in

two

s

B.O.l Inhomogeneous Dirichlet conditions

on

a rectangle

The method of shifting

the

data

can be used to transform an inhomogeneous Dirich-

let problem

to

a homogeneous Dirichlet problem. This technique works just as

it

did for a one-dimensional problem, although in two dimensions it

is

more difficult

to find a function satisfying

the

boundary conditions.

We

consider

the

BVP

-~u

=

f(x),

x

En,

{

gl(xd,

x E r

1

,

u(x) =

g2(X2),

x E r

2

,

g3(xd, x E r

3

,

g4(X2),

x E r

4

,

(B.1)

where n

is

the rectangle defined in (8.10) and

an

= r

1

U r

2

U

r3

U r

4,

as in (8.13).

We

will assume

that

the

boundary

data

are continuous,

so

gl(fd

=

g2(O),

g2(f

2

) = g3(fI),

g3(O)

= g4(f

2

),

g4(O)

= gl(O).

Suppose

we

find a function p defined on n and satisfying p(x) = g(x) for all

x

E

an.

We

then define v = u - p and note

that

-~v

=

-~u

+

~p

=

f(x)

+

~p(x)

and

v(x) = u(x) - p(x) = 0 for all x E

an

(since p satisfies the same Dirichlet conditions

that

u

is

to

satisfy).

We

can then

solve

where

-~v

=

j(x),

x E

n,

v(x) = 0, x E

an,

j(x)

=

f(x)

+

~p(x).

505

506

Appendix

B.

Shifting

the

data

in two

dimensions

The

result

will

be a

rapidly converging series

for

v,

and

then

u

will

be

given

by

u

= v + p.

We

now

describe

a

method (admittedly rather tedious)

for

computing

a

func-

tion

p

that

satisfies

the

given Dirichlet conditions.

We first

note

that

there

is a

polynomial

of the

form

which

assumes

the

desired boundary values

at the

corners:

A

direct

calculation shows

that

We

then

define

We

have thus replaced each

gi

by a

function

hi

which

differs

from

gi

by a

linear

function,

and

which

has

value zero

at the two

endpoints:

Finally,

we

define

506

Appendix

B.

Shifting

the

data

in

two dimensions

The

result will be a rapidly converging series for v, and

then

u will be given by

u = v +p.

We

now

describe a method (admittedly rather tedious) for computing a func-

tion

p

that

satisfies the given Dirichlet conditions.

We

first note

that

there is a

polynomial of the form

q(X1,

X2)

= a +

bX1

+

CX2

+

dx1X2

which assumes the desired boundary values

at

the corners:

q(O,O)

=

91(0)

= 94(0),

q(£l,O) = 91(£t) = 92(0),

q(£1,£2) =

92(£2)

= 93(£t),

q(0'£2) =

93(0)

=

94(£2).

A direct calculation shows

that

We

then define

a=91(0),

b =

91(£1)

-

91(0)

£1

'

94(£2)

-

94(0)

c=

,

£2

d =

92(£2)

+

91(0)

-

91(£t}

- 94(£2).

£1£2

(

91(£d -

91(0)

)

h

1

(X1)=91(Xl)-

91(0)+

£1

Xl,

(

92(£2)

-

92(0)

)

h2

(X2)

=

92(X2)

-

92(0)

+

£2

X2,

(

93(it) -

93(0)

)

h3(Xt} =

93(Xt}

-

93(0)

+

i1

Xl,

(

94(i2) -

94(0)

)

h4

(X2)

=

94(X2)

-

94(0)

+

£2

X2·

We

have thus replaced each 9i by a function hi which differs from 9i by a linear

function, and which has value zero

at

the two endpoints:

Finally,

we

define

Appendix

B.

Shifting

the

data

in two

dimensions

507

The

reader should notice

how the

second term interpolates between

the

boundary

values

on

FI

and

F

3

,

while

the

third term interpolates between

the

boundary values

on

F

2

and

IT^.

In

order

for

these

two

terms

not to

interfere with each other,

it is

necessary

that

the

boundary

data

be

zero

at the

corners.

It was for

this

reason

that

we

transformed

the

g^s

into

the

h^s.

The first

term

in the

formula

for p

undoes

this transformation.

It is

straightforward

to

verify

that

p

satisfies

the

desired boundary conditions.

For

example,

Thus

the

boundary condition

on

FI

is

satisfied. Similar calculations show

that

p

satisfies

the

desired boundary conditions

on the

other

parts

of the

boundary.

Example

B.I.

We

will

solve

the BVP

by

the

above

method,

where

fJ

is the

unit

square:

To

compute

p, we

define

Appendix

B.

Shifting

the

data

in

two dimensions

507

The reader should notice how

the

second term interpolates between

the

boundary

values on

r 1 and r

3,

while

the

third

term interpolates between the boundary values

on

r 2 and r

4.

In order for these two terms not

to

interfere with each other,

it

is

necessary

that

the

boundary

data

be zero

at

the corners.

It

was for this reason

that

we

transformed the gi's into the hi'S. The first term in

the

formula for p undoes

this transformation.

It

is

straightforward

to

verify

that

p satisfies the desired boundary conditions.

For example,

h3(xd - h1(xd

P(X1'0)

= a +

bX1

+

cO

+ dx10 + h1(xd +

£2

0

h

(0)

h2(0)-h4(0)

+ 4 +

£1

Xl

= a +

bX1

+ h1(xd (since h

4

(0)

= h

2

(0)

=

0)

= gl(O) +

bX1

+

gl(xd

-

(gl(O)

+

bX1)

=

gl(xd·

Thus the boundary condition on r 1

is

satisfied. Similar calculations show

that

p

satisfies

the

desired boundary conditions on

the

other

parts

of the boundary.

Example

B.1.

We will solve the

BVP

by

the

above

method, where n is the

unit

square:

To

compute p,

we

define

a=91(0)=0,

b = 91(1) - gl(O) = 1

1 '

c = 94(1) - 94(0) = 1

1 '

x E r

1

,

x E r

2

,

x E r

3

,

x E

f4

d =

g2(1)

+ gl(O) -

gl(l)

-

g4(1)

=

-2

1·1

'

h1

(Xl) =

xi

-

(0

+

xd

=

xi

- Xl,

h

2

(X2)

=

1-

x~

-

(1

+

(-I)x2)

=

X2

-

x~,

h3(xd =

(1-

X1)2

-

(1

+

(-I)X1)

=

xi

- Xl,

h4(X2)

=

X2

-

(0

+

X2)

=

o.

(B.2)

Gockenbach M.S. Partial Differential Equations. Analytical and Numerical Methods

Подождите немного. Документ загружается.