Gockenbach M.S. Partial Differential Equations. Analytical and Numerical Methods
Подождите немного. Документ загружается.


528
Appendix
C.
Solutions
to
odd-numbered
exercises
Therefore,
with
we
have
=
au(t)
+
/(*)•
Thus
u
satisfies
the
differential
equation.
We
also have
9.
(a) The
solution
is
The
population
of the first
species
(x(t))
increases exponentially, while
the
population
of the
second species
(y(t))
goes
to
zero
in finite
time (y(t)
= 0 at
t =
ln(3)/4).
Thus
the
second species becomes extinct, while
the first
species
increases without bound.
so
the
initial condition holds
as
well.
Section
4.3
1. The
solution
is
3.
The
general solution
is
5.
XQ
must
be a
multiple
of the
vector
(1,
—1).
7.
528
Therefore, with
we have
Appendix
C.
Solutions
to
odd-numbered exercises
u(t) = uoeu(t-t
o
) +
[t
eu(t-.)
f(s)
ds,
to
du (t) = auoeu(t-to) + a
[t
eu(t-.)
f(s)
ds
+
f(t)
dt
to
= au(t) +
f(t).
Thus
u satisfies
the
differential equation. We also have
[
to
u(to) = uoeu(to-t
o
) + eu(t-s)
f(s)
ds
to
=Uo
+0
=uo,
so
the
initial condition holds as well.
9.
u(t) =
~
sin
2
(t)
11. u(t) =
~
(e-
t
+ cos (t) + sin (t))
Section 4.3
1.
The
solution is
( )
1 1
-t
1 -2t
X t =
-Ul
-
-e
U2
+
-e
ll.3
v'3
V2
v'6
3.
The
general solution is
5.
Xo
must
be
a multiple of
the
vector (1,
-1).
7.
1 [
55
-
3e-
2t
- 45e-
t
+ 20t - 7 cos (t) -
11
sin (t) 1
x(t)
=
60
10
+
6e-
2t
+ 20t -
16
cos (t) - 8 sin (t)
-5
-
3e-
2t
+ 45e-
t
+ 20t - 37 cos (t) +
19
sin (t)
9.
(a)
The
solution is
3
-t
1 M 3
-t
1 M
x(t) ="2
e
+"2
e
, y(t) ="2
e
-"2e.
The
population of
the
first species (x (t)) increases exponentially, while
the
population of
the
second species (y(
t))
goes
to
zero in finite time (y(
t)
= 0
at
t = In (3)/4).
Thus
the
second species becomes extinct, while
the
first species
increases without bound.

Appendix
C.
Solutions
to
odd-numbered exercises
529
(b)
If the
initial populations
are
x(0)
= r,
y(0)
= s,
then
the
solution
to the
IVP
is
Therefore,
if r = s,
both populations decay
to
zero exponentially;
that
is,
both
species
die
out.
Section
4.4
1. (a)
Four
steps
of
Euler's method yield
an
estimate
of
0.71969.
(b)
Two
steps
of the
improved
Euler
method yield
an
estimate
of
0.80687.
(c)
One
step
of the RK4
method yields
an
estimate
of
0.82380.
Euler's method gives
no
correct digits,
the
improved Euler method gives
one
correct
digit,
and RK4
gives three correct digits. Each
of the
methods evaluated
f(t,
u)
four
times.
(b)
The
routine
ode45
from
MATLAB
(version 5.3) required
421
steps
to
produce
a
graph with
the
ending point apparently coinciding with
the
initial value.
The
graph
of
y(t) versus x(t)
is
given
in
Figure
C.4.
The
graphs
of
x(t)
and
y(t),
together with
the
times steps,
are
given
in
Figure
C.5.
They show,
not
surprisingly,
that
the
time step
is
forced
to be
small precisely when
the
coordinates
are
changing rapidly.
(c)
The
minimum step size taken
by
ode45
was
3.28
•
10~
4
,
and
using this step
length over
the
entire interval
of [0,
T]
would require almost 19000
steps.
This
is
to be
compared
to the 421
steps taken
by the
adaptive algorithm. (Note:
The
exact results
for
minimum step size, etc.,
will
differ
according
to the
algorithm
and
tolerances
used.)
5.
(a) We first
note
that
a+(ti—
to)
<
t
<
b+(ti
—
to)
if
and
only
if
a
<
t—(t\
—
to)
<b,
so
the
function
v is
well-defined.
In
fact,
(just
replace
t —
(ti
—
to) by t in the
last
step).
Appendix
C.
Solutions
to
odd-numbered exercises 529
(b)
If
the
initial populations are
x(O)
=
r,
yeO)
= s,
then
the
solution
to
the
IVP
is
x(t)
=
~
(r
+
s)e-
t
+ (r - s)e
3t
) , yet) =
~
((r +
s)e-
t
+ (s - r)e
3t
) .
Therefore, if r =
s,
both
populations decay
to
zero exponentially;
that
is,
both
species die out.
Section 4.4
1. (a) Four steps of Euler's
method
yield
an
estimate of 0.71969.
(b) Two steps of
the
improved Euler
method
yield an
estimate
of 0.80687.
(c) One step
of
the
RK4
method
yields an estimate of 0.82380.
Euler's
method
gives no correct digits,
the
improved Euler
method
gives one correct
digit,
and
RK4 gives three correct digits. Each of
the
methods evaluated
f(t,
u) four
times.
3.
(a) Let
Ul
=
X,
U2
=
dx/dt,
U3
= y,
U4
= dy/dt.
Then
the
system is
dUl
dt
=U2,
duz _
Ul
+
2U4
_
1-'2(Ul
+
I-'d
_
1-'1(Ul
-
1-'2)
dt -
rl
(Ul,
U3)3
r2(
Ul,
U3)3
'
dU3
dt
=U4,
dU4
I-'zU3
- = -
2U2
+
U3
-
----:'-------'----::-::-
dt
rl(Ul,U3)3
(b)
The
routine
ode45
from MATLAB (version 5.3) required
421
steps
to
produce
a graph with
the
ending point apparently coinciding with
the
initial value.
The
graph of yet) versus
x(t)
is given in Figure C.4.
The
graphs of x(t)
and
yet), together with
the
times steps, are given in Figure
C.5.
They
show,
not surprisingly,
that
the
time step is forced
to
be small precisely when
the
coordinates are changing rapidly.
(c)
The
minimum step size taken by
ode45
was
3.28.10-
4
,
and
using this step
length over
the
entire interval of
[0,
T] would require almost 19000 steps. This
is
to
be
compared
to
the
421
steps taken by
the
adaptive algorithm. (Note:
The
exact results for minimum step size, etc., will differ according
to
the
algorithm
and
tolerances used.)
5.
(a)
We
first note
that
a+(tl-tO)
S t S b+(lI
-to)
if
and
only if
as
t-(lI
-to)
S
b,
so
the
function v is well-defined.
In
fact,
{vet) : t E
[a
+ (lI - to), b + (tl - to)]}
={u(t-(lI-to)):
tE[a+(h-to),b+(lI-to)]}
= {u(t) : t E
[a,b]}
Gust replace t - (tl - to) by t in
the
last step).
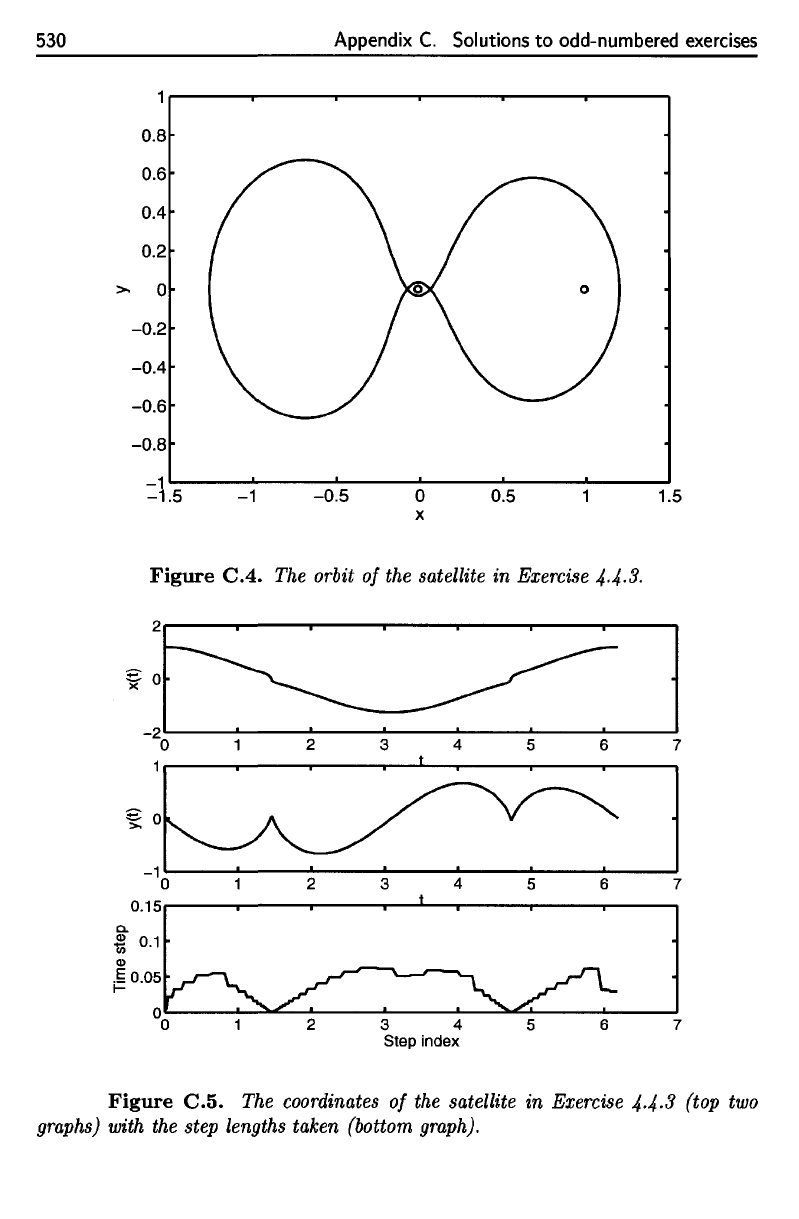
530
Appendix
C.
Solutions
to
odd-numbered
exercises
Figure
C.5.
The
coordinates
of the
satellite
in
Exercise
4-4-3
(top
two
graphs)
with
the
step lengths taken (bottom graph).
Figure
C.4.
The
orbit
of
the
satellite
in
Exercise
4-4-3-
530
Appendix
C.
Solutions
to
odd-numbered exercises
0.8
0.6
0.4
0.2
>.
0
-0.2
-0.4
-0.6
-0.8
=t5
-1
-0.5
0 0.5 1.5
x
Figure
C.4.
The orbit
of
the satellite in Exercise
4.4.3.
~JS;;:~
1
o 1 2 3 4 5 6 7
~_:~l
o 1 2 3 4 5 6 7
f:~~:;;
1
o 1 2 3 4 5 6 7
Step index
Figure
C.5.
The coordinates
of
the satellite in Exercise
4.4.3
(top two
graphs) with the step lengths taken (bottom graph).

Appendix
C.
Solutions
to
odd-numbered
exercises
531
At
1/4
1/8
1/16
1/32
1/64
1/128
Error
2.4332e-05
1.3697e-06
8.1251e-08
4.9475e-09
3.0522e-10
1.8952e-ll
By
inspection,
we see
that
as At is cut in
half,
the
error
is
reduced
by a
factor
of
approximately
16, as
expected
for
O(At
4
)
convergence.
(b)
The
following
errors were obtained
at t =
2.0:
We
have
so
v
satisfies
the
ODE. Finally,
Therefore
v is a
solution
to the
given
IVP.
(b)
Consider
the IVP
which
has
solution
u(t)
=
t
2
/2
+ l. The IVP
has
solution v(t)
=
t
2
/2
+
1/2, which
is not
equal
to
7.
The
exact solution
is
(a)
The
following
errors were obtained
at t =
0.5:
Appendix
C.
Solutions to odd-numbered exercises
We have
dv
d
-(t)
= - [u(t - (fI - to))]
dt dt
du
=
-(t
-
(h
- to))
dt
=
f(u(t
-
(t1
- to)))
=
f(v(t)),
so v satisfies
the
ODE. Finally,
V(t1) =
u(h
-
(t1
- to)) = u(to) =
Uo.
Therefore v is a solution
to
the
given IVP.
(b) Consider
the
IVP
du = t
dt
'
u(O)
=
1,
which has solution u(t) = e
/2
+
1.
The
IVP
dv
=t
dt
'
v(1) = 1
has solution
v(t) = t
2
/2
+
1/2,
which is not equal
to
7.
The
exact solution is
1
2
u(t
-
(1
- 0)) =
u(t
-
1)
=
-(t
-1)
+ 1.
2
x(t)
= { 2 -
2~-:'
0 < t < In
2,
2e,
t >
In
2.
(a)
The
following errors were obtained
at
t = 0.5:
6.t
Error
1/4
2.4332e-05
1/8
1.3697e-06
1/16
8.1251e-08
1/32
4.9475e-09
1/64
3.0522e-10
1/128
1.8952e-ll
531
By inspection,
we
see
that
as
6.t
is
cut
in half,
the
error is reduced by a factor
of
approximately 16, as expected for 0(6.t4) convergence.
(b)
The
following errors were obtained
at
t =
2.0:

532
Appendix
C.
Solutions
to
odd-numbered
exercises
At
1/4
1/8
1/16
1/32
1/64
1/128
Error
5.0774e-03
3.2345e-03
3.1896e-04
1.0063e-04
8.9026e-06
3.4808e-06
The
error definitely does
not
exhibit
O(At
4
)
convergence
to
zero.
The
reason
is
the
lack
of
smoothness
of the
function
1 + \x
—
1|; the
rate
of
convergence
given
in the
text
only
applies
to
ODEs
defined
by
smooth
functions.
When
integrating
from
t =
0tot
=
0.5,
the
nonsmoothness
of the
right-hand side
is
not
encountered since
x(t)
< 1 on
this
interval. This explains
why we
observed
good
convergence
in the first
part
of
this problem.
Section
4.5
1. (a) The
exact solution
is
(b)
The
norm
of the
error
is
approximately 0.089103.
(c)
The
norm
of the
error
is
approximately 0.10658.
3.
The
largest value
is At =
0.04.
5.
(a)
Applying
the
methods
of
Section 4.3,
we find the
solution
(b)
By
trial
and
error,
we find
that
At
<
0.02
is
necessary
for
stability. Specifically,
integrating
from
t =
0tot
=
l,n
= 49
(i.e.
At =
1/49) yields
while
n
>
50
yields
(c)
With
Xj+i
=
Xi
+
AtAxi
and
y[
l)
=
ui
•
Xj,
we
have
A
similar calculation shows
that
532
Appendix
C.
Solutions
to
odd-numbered exercises
I:l.t Error
1/4
5.0774e-03
1/8
3.2345e-03
1/16
3.1896e-04
1/32
1.0063e-04
1/64
8.9026e-06
1/128
3.4808e-06
The
error definitely does
not
exhibit O(l:l.t4) convergence
to
zero.
The
reason
is
the
lack of smoothness of
the
function 1 +
Ix
-11;
the
rate
of convergence
given in
the
text
only applies
to
ODEs defined by smooth functions. When
integrating from
t = 0
to
t = 0.5,
the
nonsmoothness of
the
right-hand side is
not encountered since
x(t)
< 1
on
this interval. This explains why
we
observed
good convergence in
the
first
part
of this problem.
Section 4.5
1. (a)
The
exact solution is
(b)
The
norm of
the
error is approximately 0.089103.
(c)
The
norm of
the
error is approximately 0.10658.
3.
The
largest value is I:l.t = 0.04.
5.
Ca)
Applying
the
methods of Section 4.3,
we
find
the
solution
1 [
3e-
t
_
e-
lOOt
]
xCt)
=
2"
3e-
t
+
e-
lOOt
.
(b) By
trial
and
error,
we
find
that
I:l.t $ 0.02 is necessary for stability. Specifically,
integrating from
t = 0
to
t = 1, n = 49 (i.e. I:l.t = 1/49) yields
while
n
:::::
50
yields
(c)
With
Xi+l =
Xi
+ I:l.tAXi
and
yii)
= Ul . Xi,
we
have
Ul .
Xi+l
= Ul .
Xi
+ I:l.tUl .
AXi
=>
yii+
1
)
=
yii)
+
I:l.t(Aut)
.
Xi
=>
yii+
1
)
=
yii)
+ I:l.tAIUl .
Xi
=>
yii+
1
)
=
yii)
+ I:l.tAlyii)
=>
yii+
1
)
=
(1
+ I:l.tAt)yii).
A similar calculation shows
that

Section
5.1
1. (a)
Since
MD is
linear,
it
suffices
to
show
that
the
null space
of MD is
trivial.
If
MDU
= 0,
then, du/dx
— 0,
that
is, u is a
constant
function:
u(x)
— c. But
then
the
condition
u(0)
= 0
implies
that
c = 0, and so u is the
zero
function.
Thus
M(M
D
]
=
{0}.
(b) If u €
CofO,
f]
and
MDU
— /,
then
we
have
Appendix
C.
Solutions
to
odd-numbered
exercises
533
For
stability,
we
need
Since
the
eigenvalues
of A are
—1,
—100,
it is not
hard
to see
that
the
upper
bound
for At is At
<
0.02, just
as was
determined
by
experiment.
(d)
For the
backward
Euler
method,
a
similar calculation shows
that
Stability
is
guaranteed
for any At,
since
for
every
At > 0.
Section
4.6
3.
The
IVP
is
The
Green's
function
is
G(t;
s)
—
e
k
^
s
\
and the
solution
is
The
mass converges,
as t
—>•
oo,
to
5.
The
solution
is
which
imply
that
Appendix
C.
Solutions
to
odd-numbered exercises
For stability,
we
need
11+~t'\11::;
1,
11+~t'\21::;
1.
533
Since
the
eigenvalues of A are
-1,
-100,
it is not
hard
to
see
that
the
upper
bound
for
~t
is
~t
::;
0.02,
just
as was determined by experiment.
(d) For
the
backward Euler method, a similar calculation shows
that
y~i+l)
=
(1-
~t,\l)-ly~i),
y~i+l)
=
(1
_
~t,\2)-ly~i).
Stability is guaranteed for any
~t,
since
for every
~t
>
O.
Section 4.6
1.
G(t; s) =
e-
2
(t-s).
3.
The
IVP
is
dm
- +
km
= 0.1,
m(O)
=
10.
dt
The
Green's function is G(t; s) =
e-k(t-s),
and
the
solution is
( )
_ (10
0.1)
-kt
0.1
mt
-
-T
e
+T·
The
mass converges, as t
-t
00,
to
0~1
~
0.289
g.
5.
The
solution is
2 .2(t) 1
u(t)
=
3"
(1
+ 2 cos (t)) sm
"2
=
3"
(cos (t) - cos
(2t»
.
Section 5.1
1.
(a) Since
Mn
is linear,
it
suffices
to
show
that
the
null space of
Mn
is trivial.
If
Mnu
= 0, then,
du/dx
=
0,
that
is, u
is
a constant function: u(x) = c.
But
then
the
condition
u(O)
= 0 implies
that
c =
0,
and
so u is
the
zero function.
Thus
N(Mn)
=
{O}.
(b)
If
u E
c1[o,
f]
and
Mnu
= f,
then
we
have
du
dx(x)=f(x),
O<x<fand
u(O)
=0,
which imply
that
u(x) =
1"
f(s)ds.

534
Appendix
C.
Solutions
to
odd-numbered
exercises
But we
also must have
u(i)
— 0,
which implies
that
If
/ €
C[Q,
I]
does
not
satisfy this condition, then
it is
impossible
for
MDU
= f
to
have
a
solution.
3.
(a) If
v,w
G S are
both solutions
of Lu = /,
then
Lv =
Lw,
or (by
linearity)
L(v —
w)
= 0.
Therefore
v — w €
A/"(Z>).
But, since
S is a
subspace,
v —
w
is
also
in S. If the
only function
in
both
Af(L)
and S is the
zero
function,
then
v
—
w
must
be the
zero
function,
that
is, v and w
must
be the
same function.
Therefore,
if
J\f(L)
n S =
{0},
then
Lu = f can
have
at
most
one
solution
for
any/.
(b)
We
have already seen
that
Lu = f has a
solution
for any / €
C[0,
f\
(see
the
discussion immediately preceding Example 5.2).
We
will
use the
result
from
the first
part
of
this exercise
to
show
that
the
solution
is
unique.
The
null space
of L is the
space
of all first
degree polynomials:
i.
Suppose
u
€
Af(L)
n S.
Then
u(x)
—
ax + b for
some
a, b € R and
Then
u(x)
= 6, and
Therefore
u is the
zero
function,
and so
A/"(L)
H
S =
{0}.
The
uniqueness
property then
follows
from
the first
part
of
this
exercise,
ii.
Suppose
u €
A/"(L)
n S.
Then
u(x)
=
ax + b for
some
o,
b
e
R and
Then
u(x)
— ax, and
Therefore
u is the
zero
function,
and so
N(L}
C\S
=
{0}.
The
uniqueness
property then
follows
from
the first
part
of
this exercise.
5.
The
condition
implies
that
du/dx
is
zero,
and
hence
that
u is
constant.
The
boundary conditions
on
u
would then imply
that
u is the
zero
function.
But,
by
assumption,
u is
nonzero
(we
assumed
that
(u, u) = 1).
Therefore,
(C.2)
cannot hold.
7.
(a) If
LmU
— 0,
then
u has the
form
u(x)
= ax + b. The first
boundary condition,
du/dx(Q)
= 0,
implies
that
a — 0, and
then
the
second boundary condition,
u(i]
= 0,
yields
6 = 0.
Therefore,
u is the
zero
function
and
M(Lm]
is
trivial.
534
Appendix
C.
Solutions
to
odd-numbered exercises
But
we
also must have
u(f)
=
0,
which implies
that
it
I(s)
ds
=
o.
If
1 E
C[O,
f] does
not
satisfy this condition,
then
it is impossible for
MDU
= 1
to
have a solution.
3.
(a)
If
v,
w E S are
both
solutions
of
Lu
=
I,
then
Lv
=
Lw,
or (by linearity)
L(v
- w) =
O.
Therefore v -
wE
N(L).
But, since S
is
a subspace, v - w is
also in
S.
If
the
only function in
both
N (L)
and
S is
the
zero function,
then
v - w must be
the
zero function,
that
is, v
and
w
must
be
the
same function.
Therefore,
if
N(L)
n S =
{O},
then
Lu
= 1 can have
at
most one solution for
any
f.
(b) We have already seen
that
Lu
= 1 has a solution for any 1 E
C[O,
f]
(see
the
discussion immediately preceding Example 5.2). We will use
the
result from
the
first
part
of this exercise
to
show
that
the
solution is unique.
The
null space of L is
the
space of all first degree polynomials:
N(L)={u:[O,f]--tR:
u(x)=ax+bforsomea,bER}.
i.
Suppose u E
N(L)
n
S.
Then
u(x)
=
ax
+ b for some a,
bE
R
and
du
(~)
= 0
=}
a =
o.
dx
2
Then
u(x)
=
b,
and
it
u(x)
dx
= 0
=}
bf
= 0
=}
b =
o.
Therefore u is
the
zero function,
and
so
N(L)
n S =
{O}.
The
uniqueness
property
then
follows from
the
first
part
of this exercise.
ii. Suppose
u E
N(L)
n
S.
Then
u(x)
=
ax
+ b for some a,
bE
R
and
u(O) = 0
=}
b =
O.
Then
u(x)
=
ax,
and
du
dx
(f)
= 0
=}
a =
O.
Therefore u is
the
zero function,
and
so
N(L)
n S =
{O}.
The
uniqueness
property
then
follows from
the
first
part
of
this
exercise.
5.
The
condition
(C.2)
implies
that
du/dx
is zero,
and
hence
that
u is constant.
The
boundary
conditions
on
u would
then
imply
that
u is
the
zero function. But, by assumption, u is nonzero
(we assumed
that
(u,u)
= 1). Therefore,
(C.2)
cannot hold.
7.
(a)
If
Lihu
=
0,
then
u has
the
form
u(x)
=
ax
+
b.
The
first boundary condition,
du/dx(O) =
0,
implies
that
a =
0,
and
then
the
second boundary condition,
u(£) =
0,
yields b =
O.
Therefore, u is
the
zero function
and
N(Lih)
is trivial.

Appendix
C.
Solutions
to
odd-numbered
exercises
535
(b)
For any /
<E
C[Q,£\,
the
function
belongs
to
C%,
[0,
i]
and
satisfies
This shows
that
L
m
u
= f has a
solution
for any / €
C7[0,^],
and
therefore
K(Lto)
=
C[0,f\.
(c)
Suppose
u,v
€
Cft[Q,£\.
Then
Thus
Lm
is
symmetric.
(d)
Suppose
A is an
eigenvalue
of Lm
with corresponding
eigenfunction
u,
and
assume
that
u has
been normalized
so
that
(u,u)
—
I.
Then
The
last
step
follows
because every nonzero
function
in
CjjO,
•£]
has a
nonzero
derivative.
9.
Define
u(x)
= x(l
—
x),
v(x)
=
x
2
(l
—
x).
Then
a
direct calculation shows
that
but
Appendix
C.
Solutions
to
odd-numbered exercises
535
(b) For any f E
C[O,
.e],
the
function
u(x) =
1£
l'
f(s)dsdz
belongs
to
c~
[O,.e]
and
satisfies
d
2
u
- dx
2
(x) =
f(x),
0 < x <
.e.
This
shows
that
Lmu
= f has a solution for any f E
C[O,
.e],
and
therefore
R(Lm)
=
C[O,.e].
(c) Suppose
u,v
E
C~[O,.e].
Then
I
t
d2
(Lmu,v) = - 0
dx~(x)v(x)dx
[
du
]1
Ii
du
dv
=-
dx(X)V(X) 0 + 0
dx(X)dx(x)dx
I
i du
dv
.
= 0 dx (x) dx (x) dx
(SInce
v(.e)
=
0,
du/dx(O) = 0)
=
[U(X):~(X)]:
-lot
U(X)::~(X)dX
I
t
d2
= - 0 u(x)
dx~
(x) dx (since
u(.e)
=
0,
dv/dx(O) = 0)
= (u, Lmv).
Thus
Lm
is symmetric.
(d) Suppose A is
an
eigenvalue of
Lm
with
corresponding eigenfunction u,
and
assume
that
u has been normalized so
that
(u, u) =
1.
Then
A = A(U,u) =
(AU,U)
= (Lmu,u)
I
i
d2
= - 0
dx~(x)u(x)dx
= -
[::(x)u(x)]:
+
li
(::(x)f
dx
1
i d 2
= 0
c:
(x))
dx (since
u(.e)
= 0, du/dx(O) =
0)
>
O.
The
last
step
follows because every nonzero function in
C~[O,.e]
has
a nonzero
derivative.
9.
Define u(x) =
x(l-
x), v(x) = x
2
(1-
x).
Then
a direct calculation shows
that
but
7
(Mu,v)
=
30'
4
(u,Mv)
=
15'

536
Appendix
C.
Solutions
to
odd-numbered
exercises
11. (a)
Suppose
u,v
€
C|[0,^].
Then
Applying
the
boundary conditions
on
u,
v,
we
obtain
(b)
If
LRU
= 0,
then
u
must
be a first
degree polynomial:
u(x)
= ax + b. The
boundary conditions imply
that
a and b
must
satisfy
the
following
equations:
The
determinant
is
computed
as
follows:
The
only solution
is a = b = 0,
that
is, u = 0, so
N(LR)
is
trivial.
Section
5.2
This
last
expression simplifies
to
four
terms, each including
the
sine
function
evalu-
ated
at an
integer multiple
of
TT,
and
hence each equal
to
zero. Thus
(u
n
,u
m
)
= 0
for
n
7^
TO.
536 Appendix
C.
Solutions
to
odd-numbered
exercises
11. (a) Suppose u, v E
C~[O,
fl.
Then
Applying
the
boundary conditions on u, v,
we
obtain
du
du
dv
dv
-K
dx
(f)v(f)
+ K dx
(O)v(O)
+ U(f)K
dx
(f)
-
U(O)K
dx
(0)
=
au(f)v(f)
+ au(O)v(O) -
au(f)v(f)
-
au(O)v(O)
=
0,
so (LRU,V) = (U,LRV), as desired.
(b)
If
LRU
=
0,
then
u must be a first degree polynomial: u(x) = ax +
b.
The
boundary conditions imply
that
a
and
b must satisfy
the
following equations:
-Ka
+ab
=
0,
(af
+
K)a
+
ab
=
O.
The determinant
is
computed as follows:
I
-K
a I
n =
-a(2K
+ af.) <
O.
a<-
+ K a
The
only solution is a = b =
0,
that
is, u =
0,
so
N(LR)
is
trivial.
Section 5.2
1.
If
n
=I-
m, then
= !li{
((n-m)1rx)
_
((n+m)1rx)}
d
2 cos f cos f x
o
=!
[ f sin
((n-m)1rx)
_ f sin
((n+m}7rx)]i.
2 (n -
m)1r
f (n +
m)1r
f 0
This last expression simplifies
to
four terms, each including
the
sine function evalu-
ated
at
an
integer multiple of
1r,
and
hence each equal to zero. Thus
(Un,
Urn)
= 0
for
n
=I-
m.

Appendix
C.
Solutions
to
odd-numbered
exercises
537
3.
The
eigenpairs
are
5.
The
characteristic polynomial
is
r
2
—
r +
(X
—
5), so the
characteristic roots
are
Case
1: A =
21/4.
In
this case,
the
characteristic roots
are r =
1/2,1/2
and the
general solution
of the ODE is
The
boundary condition
u(Q)
— 0
yields
c\ = 0, and
then
the
boundary condition
u(l)
=
1
implies
that
c<i
= 0.
Thus there
is no
nonzero solution
to the
BVP,
and
A
=
21/4
is not an
eigenvalue.
Case
2: A <
21/4.
In
this case,
the
characteristic roots, given
by
(C.3),
are
real
and
distinct.
The
general solution
of the ODE is
The
boundary conditions lead
to the
system
This system
has the
unique solution
c\ =
ci
= 0, so
there
is no
nonzero solution
for
A
<
21/4. Hence
no A <
21/4
is an
eigenvalue.
Case
3: A >
21/4.
In
this case,
the
roots
are
complex conjugate:
The
general solution
of the ODE is
The
boundary condition
u(0)
= 0
yields
c\ = 0, so any
eigenfunction
is of the
form
The
Neumann condition
at x = 1 is
equivalent
to the
equation
Although
this
equation cannot
be
solved explicitly,
a
simple graph shows
that
there
are
infinitely
many solutions
0 <
6\
< 62 < • • •,
with
Define
A&
by
Appendix
C.
Solutions
to
odd-numbered exercises
537
3.
The
eigenpairs are
(
2n
-l)1['X)
cos
2f
' n =
1,2,3,
....
5.
The
characteristic polynomial is r2 - r +
(A
- 5),
so
the
characteristic roots
are
1 - -/21 -
4A
1 + -/21 -
4A
rl
= 2 ' r2 = 2
(C.3)
Case
1:
A = 21/4.
In
this case,
the
characteristic roots are r =
1/2,1/2
and
the
general solution of
the
ODE
is
u(x) =
cle
X
/
2
+ c2xe
X
/
2
.
The
boundary
condition
u(O)
= 0 yields
CI
= 0,
and
then
the
boundary
condition
u(l)
= 1 implies
that
C2 =
O.
Thus there is no nonzero solution
to
the
BVP,
and
A = 21/4 is
not
an eigenvalue.
Case
2:
A < 21/4. In this case,
the
characteristic roots, given by (C.3), are real
and
distinct.
The
general solution of
the
ODE is
The
boundary conditions lead
to
the
system
CI
+ C2 = 0,
clne
r
! + c2r2e
r2
=
O.
This system has
the
unique solution
C1
=
C2
= 0,
so
there is no nonzero solution for
A
< 21/4. Hence no A < 21/4 is
an
eigenvalue.
Case
3:
A>
21/4.
In
this case,
the
roots are complex conjugate:
1
8'
1
8'
8=
-/4A-21
r1 =
"2
-
t,
r2 =
"2
+
z,
2'
The
general solution of
the
ODE
is
u(x) = (Clcos(8x)
+C2
sin (8x)) e
X
/
2
.
The
boundary condition
u(O)
= 0 yields
C1
= 0, so any eigenfunction is of
the
form
u(x) = sin (8x
)e
x
/
2
.
The
Neumann condition
at
x = 1 is equivalent
to
the
equation
tan
(8) =
-28,
8 >
O.
Although this equation cannot
be
solved explicitly, a simple graph shows
that
there
are infinitely many solutions
0 < 8
1
< 8
2
< ... , with
(
2k
-12k
+ 1 )
8
k
E
-2-1[',
-2-1['
, k = 1,2,
....
Define
Ak
by
8 _
-/
4A
k -
21
k - 2 '
