Gockenbach M.S. Partial Differential Equations. Analytical and Numerical Methods
Подождите немного. Документ загружается.


568
Appendix
C.
Solutions
to
odd-numbered
exercises
Figure
C.26.
The
computed solution
of
the
wave equation
in
Exercise 7.3.5.
for
t
>
to and v €
V,
where
Figure
C.25.
The
computed solution
of
the
wave equation
in
Exercise 7.3.3.
568
'E
Q)
E
Q)
u
CIl
a.
rn
'0
Appendix
C.
Solutions
to
odd-numbered exercises
0.1r-----~------~------~------~----__,
10
20
30
40
50
x
Figure
C.25.
The computed solution
of
the wave equation in Exercise 7.3.3.
'E
Q)
E
Q)
u
CIl
a.
rn
'0
1.2~------~------~------~------~------~
0.8
0.2
0.4 0.6
0.8
x
Figure
C.26.
The computed solution
of
the
wave
equation in Exercise 7.3.5.
for t
2:
to
and
v E
V,
where
v =
{v
E C
2
[O,
£]
v(O)
=
O}
.

Appendix
C.
Solutions
to
odd-numbered
exercises
569
(b)
The
system
of
ODEs
has the
same
form as in the
case
of a
homogeneous bar:
except
that
the
entries
in the
mass matrix
are now
and the
entries
in the
stiffness
matrix
are now
The
components
of the
vector
f
are
unchanged (see Section
7.3.2).
Section
7.4
1.
(a) The
fundamental frequency
is
c/(2i)
=
c/80. Therefore
(b)
We
have
c
=
T/p,
where
T is the
tension.
The
density
p is
10/40
=
0.25 g/cm,
so T is 4 •
10
8
dynes
(gcm/s
2
).
(c)
The
other resonant
frequencies
are the
integer multiples
of the
fundamental
frequency:
1000,1500,
2000,...
Hz.
3.
Snapshots
of the
solution
are
shown
in
Figure
C.27.
The
reason
that
resonance
does
not
occur
is
that
the
point source
is
placed
at a
point
of the
string
that
does
not
move under
the
fourth
standing
wave
(a fixed
point).
(In the
formula
(7.28),
sin
(rmra)
— sin
(2vr)
= 0.)
Section
8.1
1.
The
heat
equation
for a
heterogeneous medium
is
3.
For
this example,
5.
Using
the
product rule
for
scalar
functions,
we
obtain
Appendix
C.
Solutions
to
odd-numbered exercises
569
(b)
The
system of ODEs has
the
same form as in
the
case of a homogeneous bar:
_ d
2
u _ _
M dt
2
+
Ku
= f(t),
except
that
the
entries in
the
mass
matrix
are now
Mij
=
1t
p(x)cPi(x)(/Ji(x)dx,
i,j
= 1,2,
...
,
n,
and
the
entries in
the
stiffness
matrix
are now
Kij
=
1t
k(x)
d::
(x)
~!i
(x)
dx,
i,j
= 1,2,
...
, n.
The
components of
the
vector f are unchanged (see Section 7.3.2).
Section 7.4
1. (a)
The
fundamental frequency is
el(2Ji.)
=
e180.
Therefore
e
80 =
500
'*
c = 40000
cm/s
(or 400m/s).
(b)
We
have e
2
=
T/p,
whereTisthetension.
The
density
pis
10/40 =
0.25g/cm,
so T is
4.10
8
dynes
(gcm/s
2
).
(c)
The
other resonant frequencies are
the
integer multiples of
the
fundamental
frequency: 1000, 1500, 2000,
...
Hz.
3.
Snapshots of
the
solution are shown in Figure C.27.
The
reason
that
resonance
does not occur is
that
the
point source
is
placed
at
a point of
the
string
that
does
not move under
the
fourth standing wave (a fixed point). (In
the
formula (7.28),
sin (m7ra)
= sin
(27r")
= 0.)
Section 8.1
1.
The
heat equation for a heterogeneous medium is
au
p(x)e(x)
at
-
V·
(K(X)VU) =
0,
x E
n,
t > to·
3.
For this example,
[V.F=
[
F·n=1.
10
180
5.
Using
the
product
rule for scalar functions,
we
obtain
3 a a
v·
(vVu)
= L
aXi
[v
o:J
i=1
3
ov
OU
3
02U
=
'""
--
+ v
'""-2
L...J
ox; ox;
L...J
ox'
i=1
i=1'
=
Vv·
VU+
v~U.
570
Appendix
C.
Solutions
to
odd-numbered exercises
Figure
C.27.
Solution
to
(7.26) with
an
oscillatory forcing
term
(see Exer-
cise
7.4.3).
The
frequency
of
the
forcing
term
is
1044,
the
fourth natural frequency.
However,
the
solution
does
not
exhibit resonance since
the
point source
is
placed
at
a
fixed
point
of the
fourth standing wave.
—
(u,L
m
v).
The
boundary
terms
vanish
because
the
product
that
forms
the
integrand
is
zero
over
the
entire
boundary.
For
example,
since
v = 0 on
FI
and
du/dn
= 0 on
F2.
7.
Suppose
u,v
G
C™(O).
Then
570
-7
2.5
x
10
2
1.5
0.5
Oli;;:::------:::::I.
-0.5
-1
-1.5
-2
Appendix
C.
Solutions
to
odd-numbered exercises
co
=
1044
-2.5
0
'-----0
......
-2----0
....
.4----0
.....
6----0
....
8-----'
x
Figure
C.27.
Solution to (7.26) with an oscillatory forcing term (see Exer-
cise
7.4.3). The frequency
of
the forcing term is 1044, the fourth natural frequency.
However, the solution
does
not exhibit resonance since the point source is placed at
a fixed point
of
the fourth standing wave.
7.
Suppose u, v E
C~
(n).
Then
(Lmu,v) = -
In
v.6.u
= {
Vu·
Vv
-1
v:
(Green's first identity)
in
an
=
In
Vu·Vv
= { u
a
av
- {
u.6.v
(Green's first identity)
ian
n
in
= -
In
u.6.v
= (u,Lmv).
The
boundary
terms
vanish because
the
product
that
forms
the
integrand
is
zero
over
the
entire boundary. For example,
{ v
au
= 0
ian
an
since v = 0
on
fl
and
au/an
= 0 on f
z
.
Appendix
C.
Solutions
to
odd-numbered
exercises
571
Section
8.2
1. (a)
(b)
The
graphs
of the
error
are
given
in
Figure
C.28.
Figure
C.28.
The
error
in
approximating
f(x,y)
by the first 4
terms (top)
and
the first 25
terms (bottom)
of the
double
Fourier sine series. (See Exercise
8.2.1.)
3. The
solution
is
given
by
where
the
c
mn
are the
coefficients
from
Exercise
1 and
Appendix
C.
Solutions
to
odd-numbered exercises
Section 8.2
1. (a)
(b)
The
graphs of
the
error are given in Figure C.28.
X
10
-3
o 0
0.2
2
571
Figure
C.28.
The error
in
approximating
f(x,y)
by
thefirst4
terms (top)
and the first
25
terms (bottom)
of
the double Fourier sine series. (See Exercise
8.2.1')
3.
The
solution is given
by
00
00
u(x) = L L
~mn
sin (m7rXl) sin
(n7rX2),
I\mn
m=l
n=l
where
the
Cmn
are
the
coefficients from Exercise 1
and

572
Appendix
C.
Solutions
to
odd-numbered
exercises
5.
(a)
ThelBVPis
The
domain
$1
is the
rectangle
(b)
The
solution
is
where
(c)
The
steady-state
temperature
u
s
(x)
satisfies
the BVP
The
solution
is
(d)
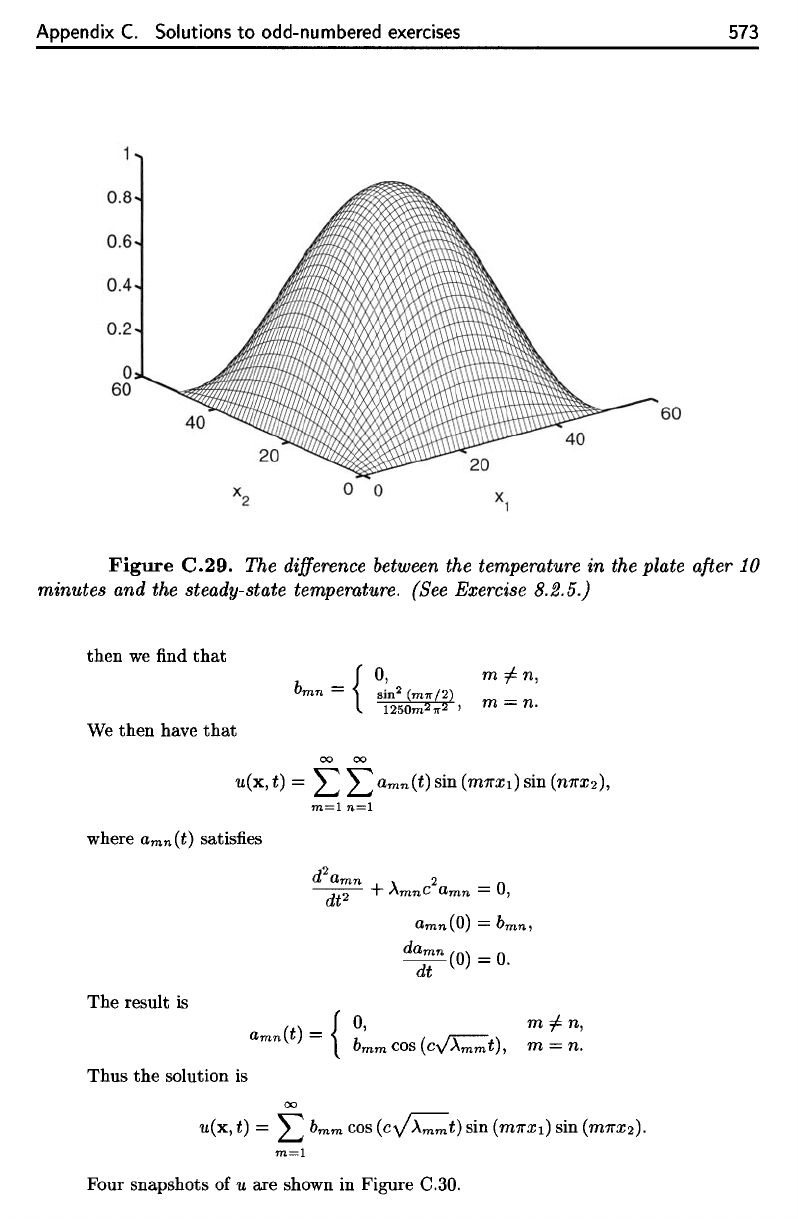
The
maximum
difference
between
the
temperature after
10
minutes
and
th
steady-state
temperature
is
about
1
degree.
The
difference
is
graphed
in
Figur
C.29.
7.
The
minimum temperature
in the
plate
reaches
4
degrees Celsius after
825
seconds
9.
The
leading edge
of the
wave
is
initially
2/5
units
from
the
boundary,
and th
wave
travels
at a
speed
of
261-\/2
units
per
second. Therefore,
the
wave reaches
th
boundary
after
V^/1305
=
0.00108 seconds. Figure
8.6
shows
the
wave about
t<
reach
th e
boundary after
10~
3
seconds.
11.
The
difficult
task
is to
compute
the
Fourier
coefficients
of the
initial
displacemen
ill.
If we
write
572 Appendix
C.
Solutions
to
odd-numbered exercises
5.
(a)
The
IBVP is
au
pc
at
- KC!..U = 0.02, x E
n,
t >
0,
u(x,O) =
5,
x E
n,
u(x,
t) =
0,
x E
an,
t >
O.
The
domain n is
the
rectangle
{x
E
R2
: 0 <
Xl
<
50,
0 <
X2
< 50} .
(b)
The
solution is
~ ~
. (m7rXl) .
(n7rX2)
u(x, t) =
L...J L...J
amn(t)
sm
-w
sm
50
'
m=l n=l
where
(t)
=
(b
_ Cmn )
-t<Arnnt/(pc)
+ C
mn
a
mn
mn
\ e \ ,
KAmn
K~mn
b
mn
=
20
(-1
+
(_I)m)
(-1
+
(_I)n)
,
mn7r
2
2
(-1
+
(_1)m)
(-1
+
(-It)
Cmn =
25mn7r
2
'
(m
2
+ n
2
)7r
2
Amn
= 2500
(c)
The
steady-state
temperature
Us
(x) satisfies
the
BVP
The
solution is
-KC!..U
= 0.02, x E
n,
u(x)
= 0, x E
an.
()
~~
Cmn . (m7rXl) .
(n7rX2)
Us
X =
L...J L...J
KAmn
sm
-w
sm
50
.
m=l
n=l
(d)
The
maximum difference between
the
temperature
after
10
minutes
and
the
steady-state
temperature
is
about
1 degree.
The
difference is graphed in Figure
C.29.
7.
The
minimum
temperature
in
the
plate reaches 4 degrees Celsius after
825
seconds.
9.
The
leading edge of
the
wave is initially 2/5 units from
the
boundary,
and
the
wave travels
at
a speed of 261..;2 units per second. Therefore,
the
wave reaches
the
boundary
after ..;2/1305
~
0.00108 seconds. Figure 8.6 shows
the
wave
about
to
reach
the
boundary
after
10-
3
seconds.
11.
The
difficult task is
to
compute
the
Fourier coefficients of
the
initial displacement
?jJ.
If
we
write
00
00
?jJ(x)
=
2: 2:
b
mn
sin (
m7rX
l)
sin (
n7rX
2)
,
m=l n=l
Appendix
C.
Solutions
to
odd-numbered
exercises
573
Figure
C.29.
The
difference
between
the
temperature
in the
plate
after
10
minutes
and the
steady-state temperature. (See Exercise 8.2.5.)
then
we find
that
We
then have
that
where
a
mn
(t)
satisfies
The
result
is
Thus
the
solution
is
Four
snapshots
of u are
shown
in
Figure
C.30.
Appendix
C.
Solutions
to
odd-numbered exercises
573
60
o 0
x,
Figure
C.29.
The difference between the temperature in the plate after 10
minutes and the steady-state temperature. (See Exercise
8.2.5.)
then
we
find
that
We
then
have
that
00
00
0,
ain
2
(mrr/Z)
lZ50m
2
rr2 ,
m=/=-n,
m=n.
u(x,t)
= L L
a
mn(t)sin(mll'x
1
)sin(mrx
z
),
where amn(t) satisfies
The
result is
m=l
n=l
dZa
mn
2
dt2
+
Amn
C
a
mn
= 0,
amn(O)
= b
mn
,
damn
(0) =
o.
dt
amn(t)
= {
°b'
(n---
)
mm
cos
Cy
Ammt ,
m=/=-n,
m=n.
Thus
the
solution is
00
u(x,
t) = L b
mm
cos (CVAmmt) sin (mll'Xl) sin (mll'xz).
m=l
Four snapshots of u are shown in Figure C.30.
574
Appendix
C.
Solutions
to
odd-numbered
exercises
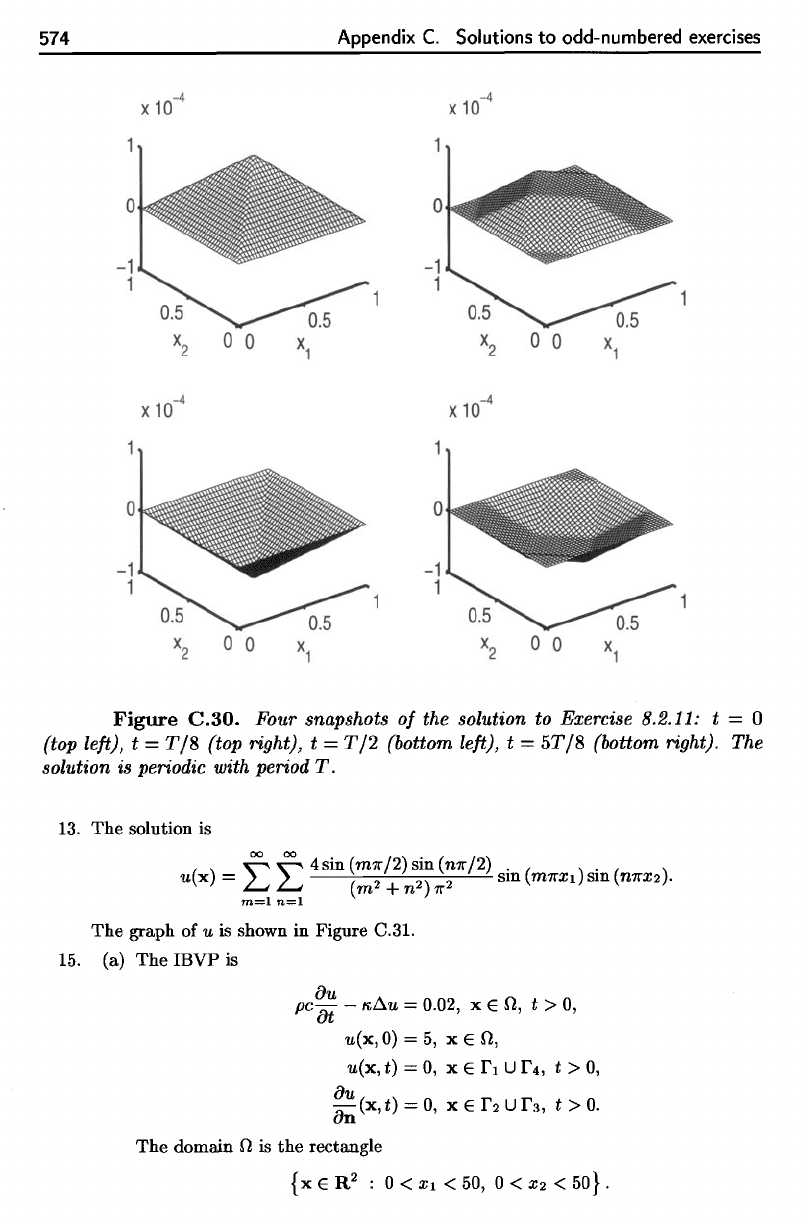
Figure
C.30.
Four snapshots
of the
solution
to
Exercise 8.2.11:
t = 0
(top
left),
t =
T/8
(top
right),
t =
T/1
(bottom
left),
t =
5T/8 (bottom right).
The
solution
is
periodic with period
T.
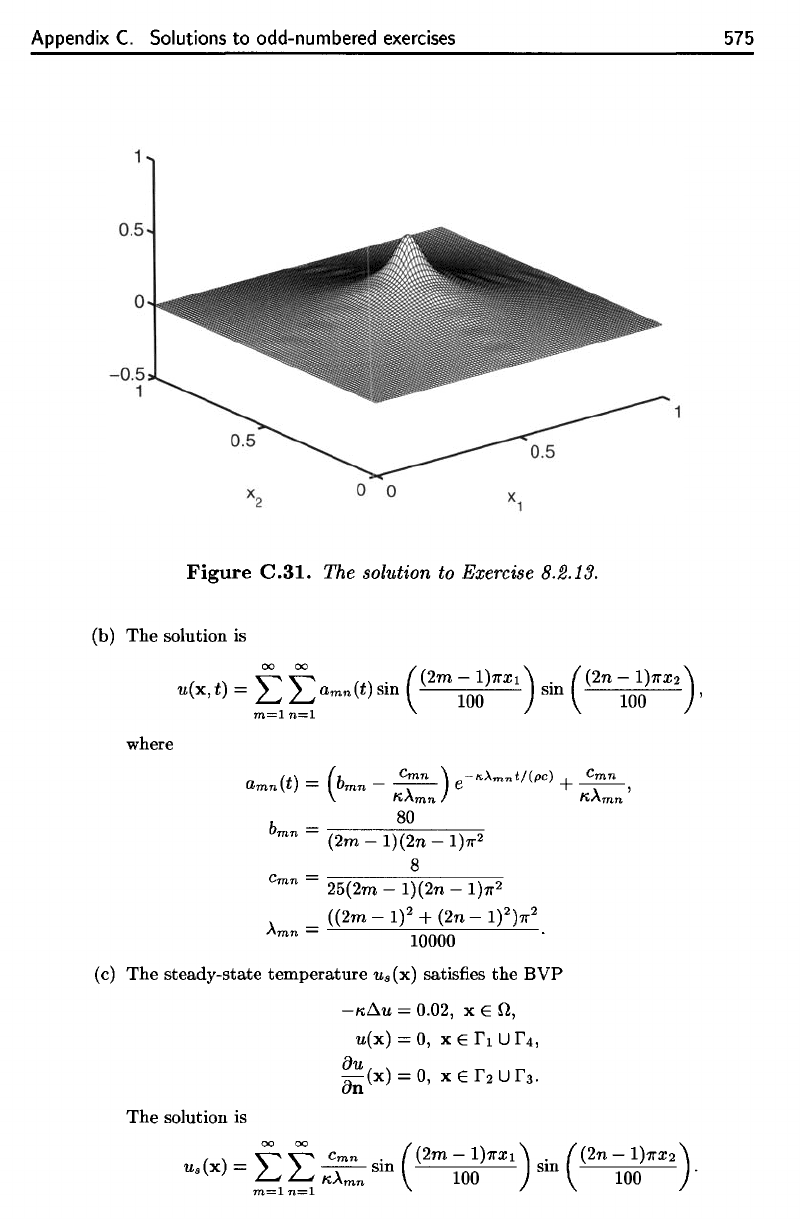
13. The
solution
is
The
graph
of u is
shown
in
Figure
C.31.
15.
(a)
ThelBVPis
The
domain
O
is the
rectangle
574
-1
1
-1
1
X
10-4
X
10
-4
Appendix
C.
Solutions
to
odd-numbered exercises
-1
1
-1
1
Figure
C.30.
Four snapshots
of
the solution to Exercise 8.2.11: t = 0
(top left), t =
T/8
(top right), t =
T/2
(bottom left), t =
5T/8
(bottom right). The
solution is periodic with period
T.
13
.
The
solution is
00
00
4sin(m7r/2)sin(mr/2)
. .
u(x) = L L
(m
2
+ n
2
)
7r
2
sm (m7rxI) sm (n7rX2).
m
=l
n=l
The
graph of u is shown in Figure
C.3l.
15
. (a)
The
IBVP
is
au
pc
at
-
K~U
= 0.02, x E 0 , t > 0,
u(x,
0)
= 5, x E
0,
u(x,t)
=0
,
xEr}Ur
4
,
t>O,
au
an
(x, t) =
0,
x E
r2
U
r3,
t > O.
The
domain ° is
the
rectangle
{x
E R2 : 0 <
Xl
<
50,
0 <
X2
< 50} .
Appendix
C.
Solutions
to
odd-numbered
exercises
575
Figure
C.31.
The
solution
to
Exercise
8.2.13.
(b)
The
solution
is
where
(c)
The
steady-state
temperature
u
s
(x)
satisfies
the BVP
The
solution
is
Appendix
C.
Solutions
to
odd-numbered exercises
0.5
o
-0
.5
1
o 0
Xl
Figure
C.31.
The solution
to
Exercise 8.2.13.
(b)
The
solution is
(
t)
= ~
~
(t)·
(2m
-1)
JrX
l)
.
(2n
-1)
JrX
2)
u
x,
~
~amn
sm 100 sm 100 '
m=l
n=l
where
amn(t)
=
(b
mn
_
C~n
)
e-I<A",nt/(pC)
+
C~n
,
~Amn
KAmn
80
b
mn
=
.,......----0-.,......----,-_o_
(2m
- 1)(2n - 1)Jr
2
8
C
mn
=
.,----,.,.----:-.,...,.....---;---;:-
25(2m - 1)(2n - 1)Jr
2
A _
«2m
- 1)2 +
(2n
- 1)2)Jr
2
mn
- 10000 .
(c)
The
steady-state
temperature
us(x)
satisfies
the
BVP
-,,~u
= 0.02, x E
n,
The
solution is
u(x)
=
0,
x E
fl
U
f4,
au
an
(x) = 0, x E
f2
U
fa.
( )
_
~~
Cmn
•
(2m-l)JrXl)
.
(2n-l)JrX2)
Us
x -
~ ~
"Amn
sm 100 sm 100 .
m=l
n=l
575
576
Appendix
C.
Solutions
to
odd-numbered
exercises
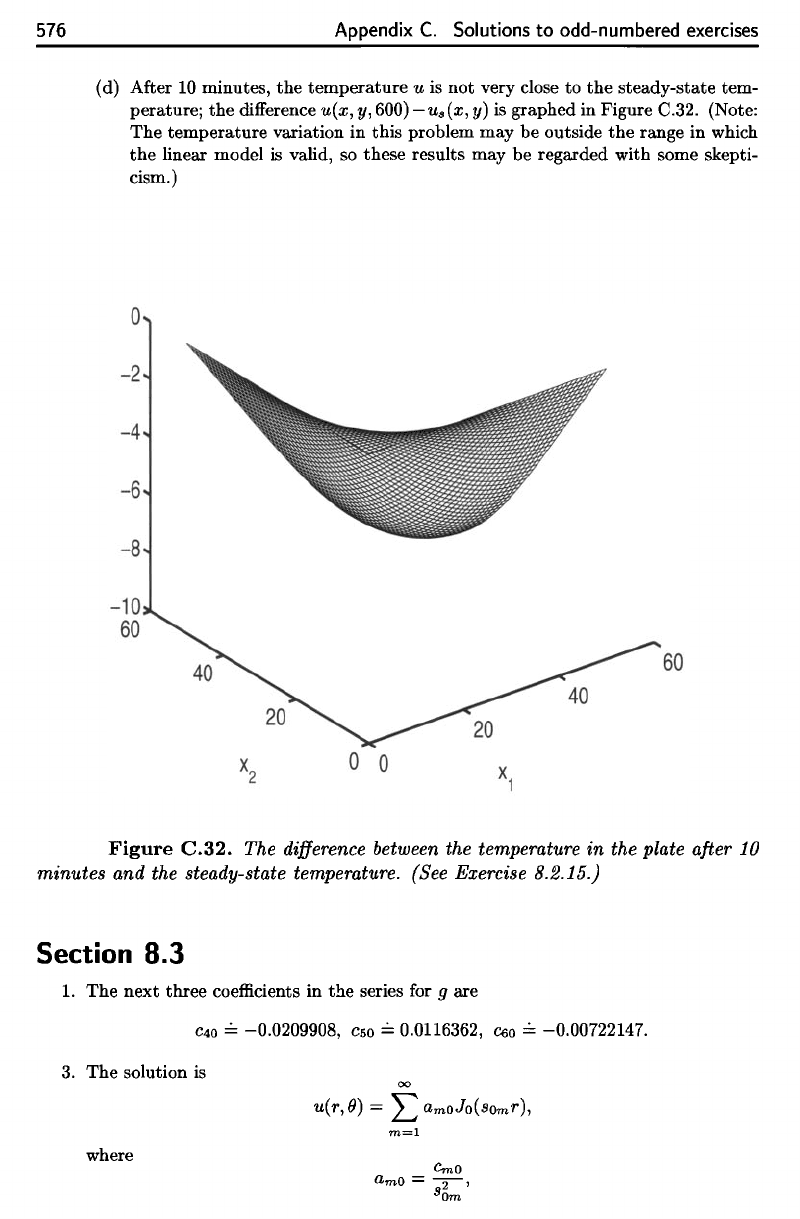
(d)
After
10
minutes,
the
temperature
u is not
very close
to the
steady-state
tem-
perature;
the
difference
u(x,
y,
600)
—u
s
(x,
y)
is
graphed
in
Figure
C.32.
(Note:
The
temperature variation
in
this problem
may be
outside
the
range
in
which
the
linear model
is
valid,
so
these results
may be
regarded with some skepti-
cism.)
Figure C.32.
The
difference
between
the
temperature
in the
plate
after
10
minutes
and the
steady-state
temperature.
(See
Exercise
8.2.15.)
Section
8.3
1. The
next three
coefficients
in the
series
for g are
3.
The
solution
is
where
576
Appendix
C.
Solutions
to
odd-numbered
exercises
(d) After
10
minutes,
the
temperature
u is not very close
to
the
steady-state tem-
perature;
the
difference u(x, y, 600)
-u.(x,
y) is graphed in Figure C.32. (Note:
The
temperature
variation in this problem may be outside
the
range in which
the
linear model
is
valid, so these results may be regarded with some skepti-
cism.)
o
-2
-4
-6
-8
-10
60
60
o 0
Figure
C.32.
The difference between the temperature in the plate after
10
minutes and the steady-state temperature. (See Exercise 8.2.15.)
Section 8.3
1.
The
next three coefficients in
the
series for 9 are
C40
~
-0.0209908, C50
~
0.0116362, C60
~
-0.00722147.
3.
The
solution is
where
00
u(r,
B)
= L
amoJO(SOm
r
),
m=l
Cmo
amo
=
-2-'
sOm
Appendix
C.
Solutions
to
odd-numbered
exercises
577
the
c
m
o
are the
coefficients
of
/(r,
0) = 1
—
r, and the som are the
positive roots
of
Jo. A
direct calculation shows
that
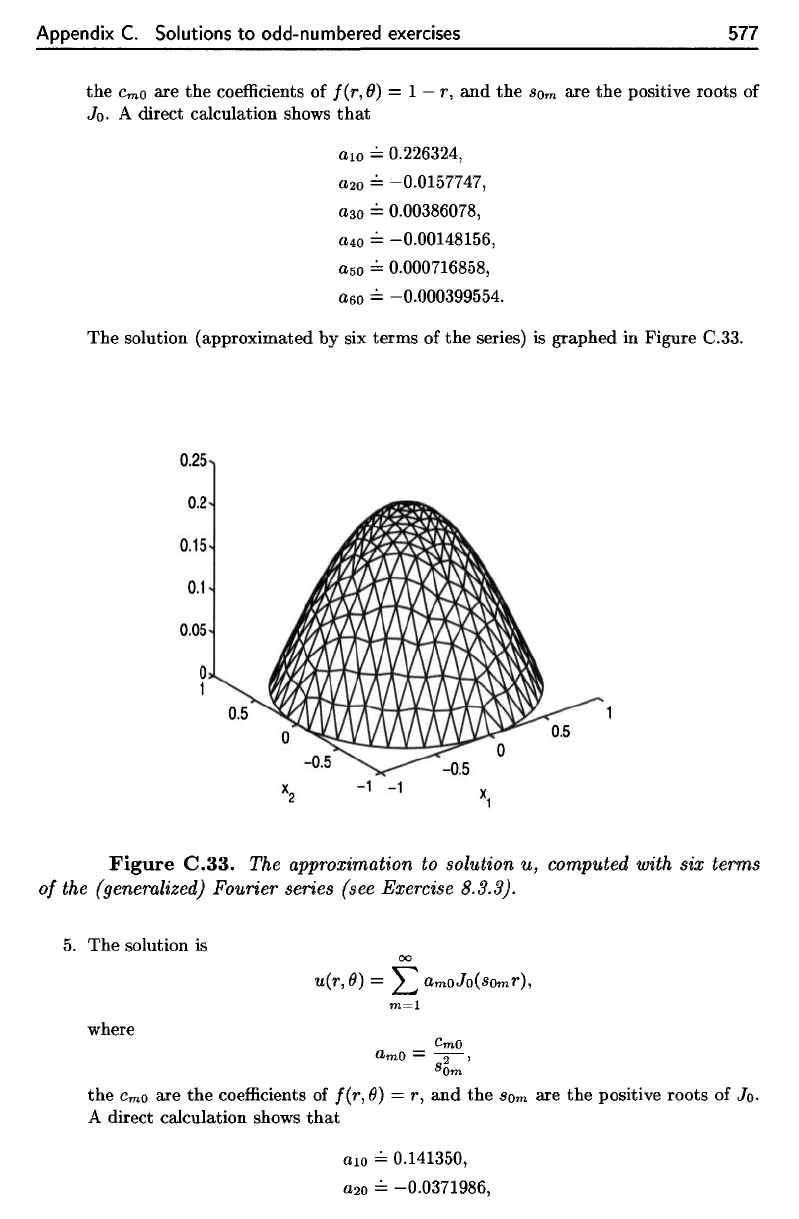
The
solution (approximated
by six
terms
of the
series)
is
graphed
in
Figure
C.33.
Figure
C.33.
The
approximation
to
solution
u,
computed with
six
terms
of
the
(generalized) Fourier series (see Exercise
8.3.3).
5.
The
solution
is
where
the
Cmo
are the
coefficients
of
/(r,
0) = r, and the
so
m
are the
positive roots
of
JQ.
A
direct calculation shows
that
Appendix
C.
Solutions
to
odd-numbered
exercises
577
the
Cmo
are
the
coefficients
of
f(r, 9) = 1 -
r,
and
the
SOm are
the
positive roots of
J
o
.
A direct calculation shows
that
alO
==
0.226324,
a20
==
-0.0157747,
a30
==
0.00386078,
a40
==
-0.00148156,
a50
==
0.000716858,
a60
==
-0.000399554.
The
solution (approximated
by
six
terms
of
the
series) is graphed in Figure C.33.
0.25
0.2
0.
15
0.1
0.
05
o
1
- 1
-1
Xl
Figure
C.33.
The approximation to solution
u,
computed with six terms
of
the (genemlized) Fourier series (see Exercise 8.3.3).
5.
The
solution is
where
00
u(r,9)
= L
amoJO(SOm
r
),
m=l
Cmo
amo =
-2-'
sOm
the
CmO are
the
coefficients of f(r, 9) = r,
and
the
80m
are
the
positive roots of
Jo.
A direct calculation shows
that
alO
==
0.141350,
a20
==
-0.0371986,
