Gockenbach M.S. Partial Differential Equations. Analytical and Numerical Methods
Подождите немного. Документ загружается.

578
Appendix
C.
Solutions
to
odd-numbered
exercises
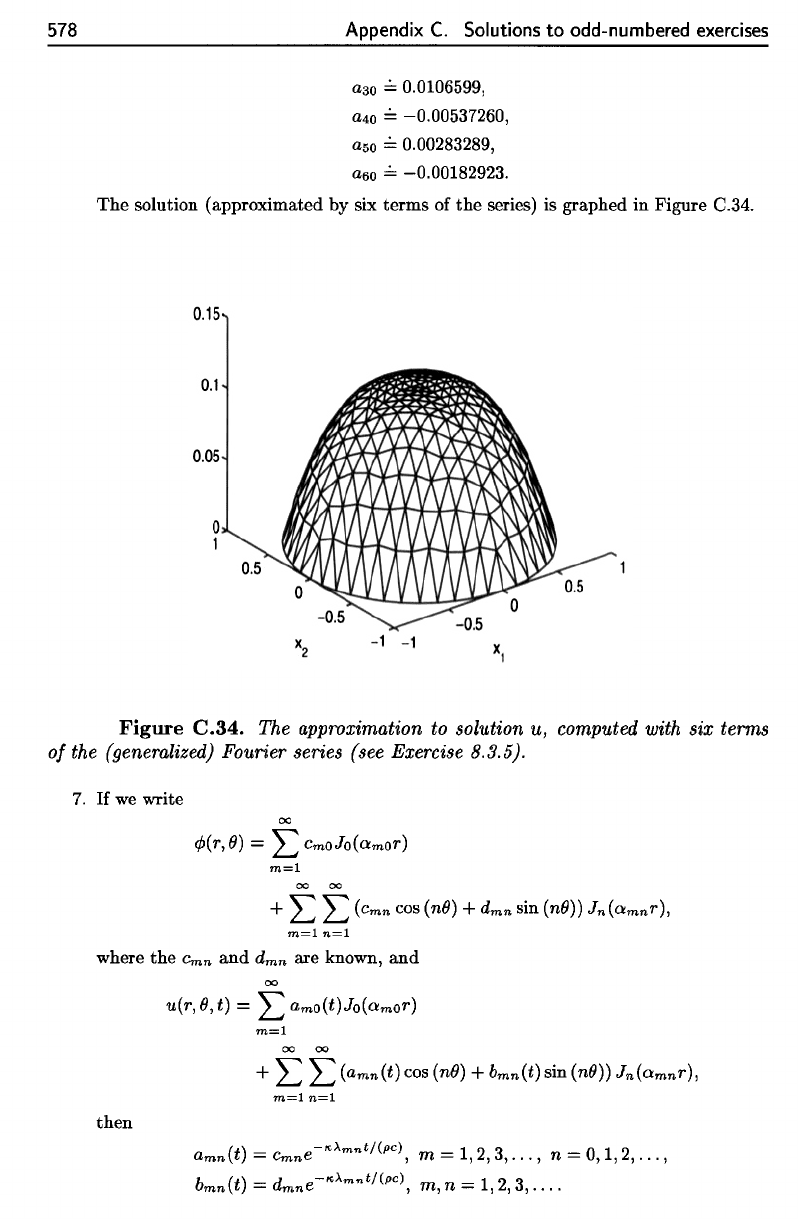
Figure
C.34.
The
approximation
to
solution
u,
computed
with
six
terms
of
the
(generalized)
Fourier series
(see
Exercise 8.3.5).
7. If we
write
then
The
solution (approximated
by six
terms
of the
series)
is
graphed
in
Figure
C.fr
where
the
c
mn
and
d
mn
are
known,
and
578
Appendix
C.
Solutions
to
odd-numbered exercises
a30
==
0.0106599,
a40
==
-0.00537260,
a50
==
0.00283289,
a60
==
-0.00182923.
The
solution (approximated
by
six terms of
the
series) is graphed in Figure C.34.
0.
15
0.1
0.05
o
1
-1
-1
x,
Figure
C.34.
The approximation to solution u, computed with six terms
of
the (generalized) Fourier series (see Exercise 8.3.5).
7.
If
we
write
00
¢(r,8)
= L
cmoJO(OmO
r
)
m=l
00 00
+ L L
(C
mn
cos (n8) + d
mn
sin (n8)) In(Omn
r
),
m=l
n=l
where
the
C
mn
and
d
mn
are known,
and
00
u(r, 8, t) = L
amo(t)JO(OmO
r
)
m=l
00
00
+ L L (amn(t) cos (n8) + bmn(t) sin (n8)) In(Omn
r
),
m=l
n=l
then
(t)
-
-t<Arnnt/(pC)
- 1 2 3 - 0 1 2
a
mn
- Cmne , m - , , ,
...
, n - , , ,
...
,
bmn(t) =
dmne-t<Arnnt/(PC),
m, n =
1,2,3,
....

Appendix
C.
Solutions
to
odd-numbered
exercises
579
However,
since
0(r,
9} — r(l
—
r) cos
(#)/5
(a
function
of r
times
cos
(6)),
all of the
coefficients
of
<f)
are
zero except
for
Therefore,
Figure
C.35.
The
approximation
to
solution
u at t = 30,
computed
with
one
term
of the
(generalized)
Fourier
series
(see
Exercise
8.3.7).
9.
A
circular drum
of
radius
A has
area
nA
2
,
the
same area
as a
square drum
of
side
length
^/TrA.
The
fundamental
frequency
of
such
a
square drum
is
Comparing
to
Example 8.9,
we see
that
the
circular drum sounds
a
lower
frequency
than
a
square drum
of
equal
area.
with
a
m
i(£)
given above.
After
30
seconds,
the
temperature distribution
can be
approximated accurately using
a
single eigenfunction (corresponding
to the
largest
eigenvalue, An),
so we
need only
The
temperature distribution
after
30
seconds
is
graphed
in
Figure C.35.
Appendix
C.
Solutions to odd-numbered exercises
579
However, since
</J(r,
0)
=
r(l
-
r)
cos (0)/5 (a function of r times cos (0)), all of
the
coefficients of
</J
are zero except for
Cml,
m =
1,2,3,
....
Therefore,
00
u(r,
0,
t)
= L
aml(t)
cos
(O)Jl(amlr),
m=l
with
aml(t)
given above. After 30 seconds,
the
temperature
distribution can be
approximated accurately using a single eigenfunction (corresponding
to
the
largest
eigenvalue,
AU),
so
we
need only
Cll
~
9.04433.
The
temperature
distribution after
30
seconds is graphed in Figure C.35.
10
-10
-10
Figure
C.35.
The approximation
to
solution u at t = 30, computed with
one term
of
the (generalized) Fourier series
(see
Exercise 8.3.7).
9.
A circular
drum
of
radius A has
area
7l'A2,
the
same area as a square
drum
of side
length
"fir
A.
The
fundamental frequency of such a square
drum
is
C
Comparing
to
Example 8.9,
we
see
that
the
circular
drum
sounds a lower frequency
than
a square
drum
of equal area.
580
Appendix
C.
Solutions
to
odd-numbered
exercises
Section
8.4
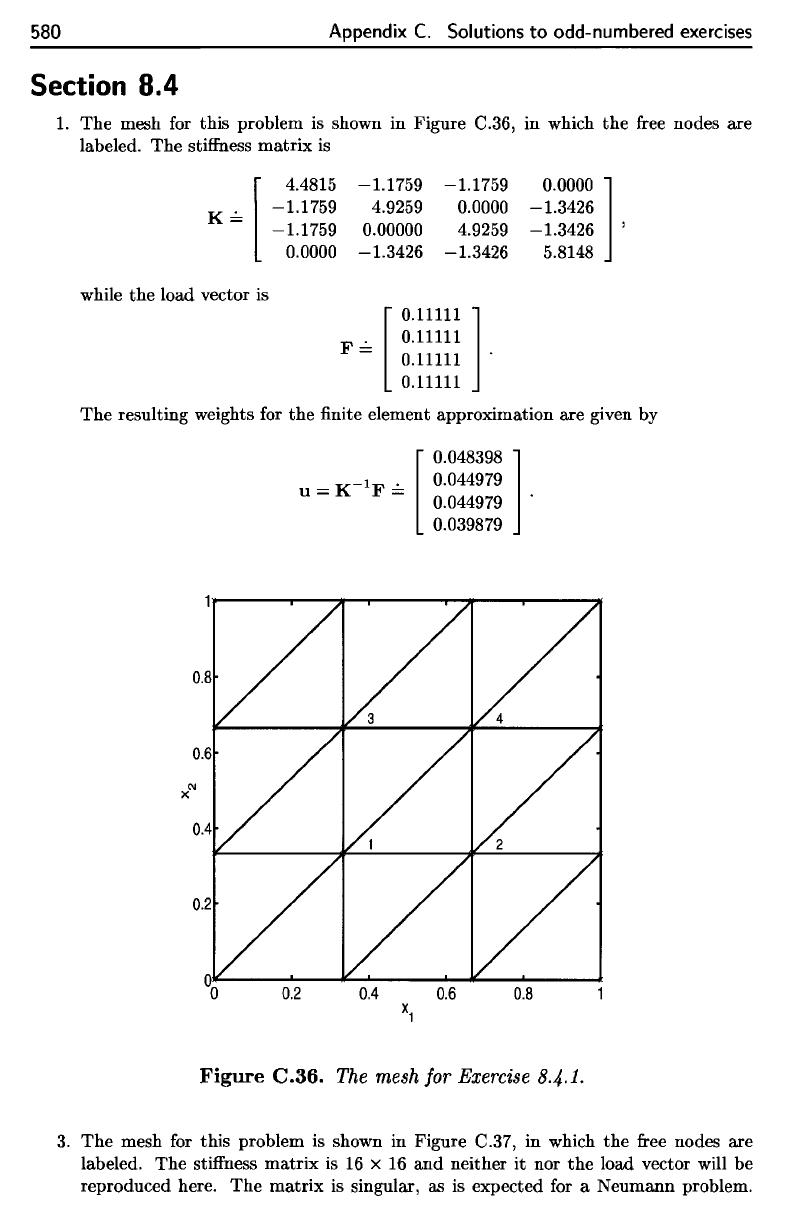
1. The
mesh
for
this problem
is
shown
in
Figure
C.36,
in
which
the
free
nodes
are
labeled.
The
stiffness
matrix
is
The
resulting weights
for the finite
element approximation
are
given
by
Figure C.36.
The
mesh
for
Exercise
8.4-1-
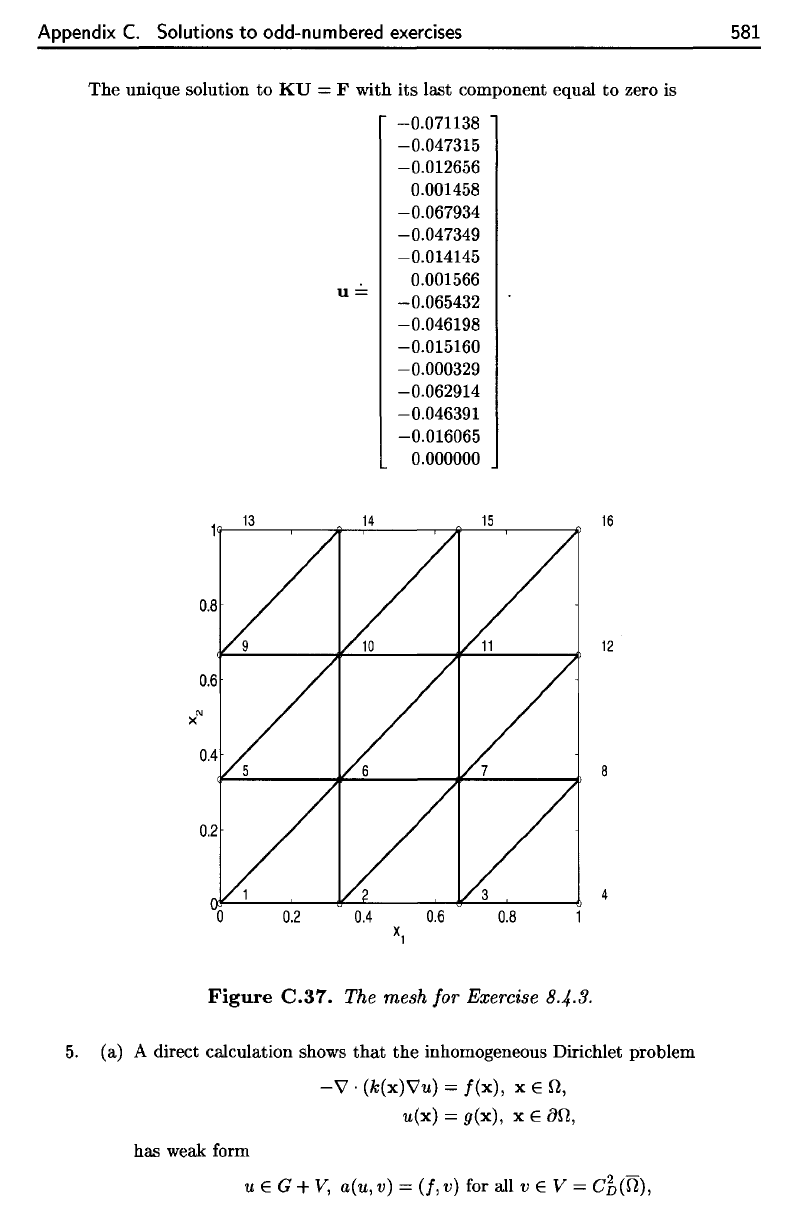
3.
The
mesh
for
this problem
is
shown
in
Figure
C.37,
in
which
the
free
nodes
are
labeled.
The
stiffness
matrix
is 16 x 16 and
neither
it nor the
load vector
will
be
reproduced here.
The
matrix
is
singular,
as is
expected
for a
Neumann problem.
while
the
load vector
is
580
Appendix
C.
Solutions
to
odd-numbered exercises
Section 8.4
1.
The
mesh for this problem is shown in Figure C.36, in which
the
free nodes are
labeled.
The
stiffness
matrix
is
K
~
-1.1759
[
4.4815
-1.1759
0.0000
while
the
load vector is
-1.1759
4.9259
0.00000
-1.3426
-1.1759
0.0000
4.9259
-1.3426
[
0.11111 ]
F
~
0.11111
0.11111 .
0.11111
0.0000 ]
-1.3426
-1.3426
'
5.8148
The
resulting weights for
the
finite element approximation are given by
[
0.048398]
=
K-1F
~
0.044979
u 0.044979 .
0.039879
Figure
C.36.
The mesh for Exercise 8.4.1.
3.
The
mesh for this problem is shown in Figure C.37, in which
the
free nodes are
labeled.
The
stiffness
matrix
is
16
x
16
and
neither
it
nor
the
load vector will be
reproduced here.
The
matrix
is singular, as is expected for a Neumann problem.
Appendix
C.
Solutions
to
odd-numbered
exercises
581
The
unique solution
to KU = F
with
its
last
component equal
to
zero
is
Figure
C.37.
The
mesh
for
Exercise
8-4-3.
5.
(a) A
direct calculation shows
that
the
inhomogeneous Dirichlet problem
has
weak
form
Appendix
C.
Solutions
to
odd-numbered exercises
The
unique solution
to
KU
= F with its last component equal
to
zero is
-0.071138
-0.047315
-0.012656
0.001458
-0.067934
-0.047349
-0.014145
0.001566
u=
-0.065432
-0.046198
-0.015160
-0.000329
-0.062914
-0.046391
-0.016065
0.000000
16
12
4
o
0.2
0.4
0.6
0.8
Xl
Figure
C.37.
The mesh for Exercise 8.4.3.
5.
(a) A direct calculation shows
that
the
inhomogeneous Dirichlet problem
has weak form
-V'.
(k(x)V'u) =
f(x),
x E
n,
u(x) = g(x), x
EOn,
u E G +
V,
a(u,v)
=
(f,v)
for all v E V =
eben),
581

582
Appendix
C.
Solutions
to
odd-numbered
exercises
where
G is any
function
satisfying
the
condition
G(x)
=
p(x)
for x €
dQ,
and
Substituting
u — G +
w,
where
w
G
V,
into
the
weak
form
yields
In
the
Galerkin method,
we
replace
V by a finite-dimensional
subspace
V
n
and
solve
When using piecewise linear
finite
elements,
we can
satisfy
the
boundary con-
ditions approximately
by
taking
G to be a
continuous piecewise linear
function
whose
values
at the
boundary nodes agree with
the
given boundary
function
g. For
simplicity,
we
take
G to be
zero
at the
interior nodes.
The
resulting
load vector
is
then given
by
Since
G is
zero
on
interior nodes,
the
quantity
a(G,
&)
is
nonzero only
if
(free)
node
i
belongs
to a
triangle adjacent
to the
boundary.
(b)
The
regular triangulation
of the
unit square having
18
triangles
has
only
four
interior
(free)
nodes,
and
each
one
belongs
to
triangles adjacent
to the
bound-
ary.
This
means
that
every entry
in the
load vector
is
modified
(which
is not
the
typical
case).
Since
/ = 0, the
load vector
f is
defined
by
The
load vector
is
while
the
solution
to Ku = f is
7.
(a)
Consider
the BVP
Multiplying
the PDE by a
test
function
v € V =
C
2
(O)
and
applying Green's
first
identity yields
582
Appendix
C.
Solutions
to
odd-numbered exercises
where G is any function satisfying
the
condition G(x) = g(x) for x E
an,
and
G + V = {G + v : v E
V}
.
Substituting
u = G + w, where w E V,
into
the
weak form yields
wE
V,
a(w,v)
=
(f,
v) - a(G,v) for all v E
V.
In
the
Galerkin
method,
we replace V by a finite-dimensional subspace
Vn
and
solve
wE
V
n
,
a(w,v)
=
(f,v)
-a(G,v)
for all v E V
n
.
When
using piecewise linear finite elements, we
can
satisfy
the
boundary
con-
ditions approximately
by
taking
G
to
be
a continuous piecewise linear function
whose values
at
the
boundary
nodes agree
with
the
given
boundary
function
g. For simplicity, we
take
G
to
be
zero
at
the
interior nodes.
The
resulting
load vector is
then
given by
Ii
=
(f,
CPi)
- a(G,
cp;),
i =
1,2,3,
...
, n.
Since G is zero on interior nodes,
the
quantity
a(G,
CPi)
is nonzero only if (free)
node
i belongs
to
a triangle adjacent
to
the
boundary.
(b)
The
regular triangulation
of
the
unit
square having 18 triangles has only four
interior (free) nodes,
and
each one belongs
to
triangles adjacent
to
the
bound-
ary. This means
that
every
entry
in
the
load vector is modified (which is not
the
typical case). Since I =
0,
the
load vector f is defined
by
f; = -a(G,CPi), i =
1,2,3,4.
The
load vector is
[
0.22222222222222]
f
==
1.55555555555556
0.22222222222222 '
1.55555555555556
while
the
solution
to
Ku
= f is
[
0.27777777777778]
...:...
0.61111111111111
u - 0.27777777777778 .
0.61111111111111
7.
(a) Consider
the
BVP
-V·
(k(x)Vu)
=
I(x),
in
0"
au
an
(x) =
h(x),
x
Eon.
(C.5)
Multiplying
the
PDE
by
a
test
function v E V = C
2
(TI)
and
applying Green's
first identity yields
1
kVu
.
Vv
= r
Iv
+ r
kvh
for all v E
V.
n
in
ion

Appendix
C.
Solutions
to
odd-numbered
exercises
583
Writing
and
We
will
apply Galerkin's method with
V
m
equal
to the
space
of all
continuous
piecewise
linear
function
relative
to a
given triangulation
T. We
label
the
standard
basis
of
V
m
as
</>i,
02,
- -
-,
<f>
n
,
and the
nodes
as
zi,
Z2,...,
z
n
.
(Every
node
in the
mesh
is now
free.)
Thus
V
n
—
span{0i,^2,
• -
-,
(j>
n
}-
We
then
define
the
Galerkin approximation
w
n
by
we
obtain
the
system
Kw
=
F. The
stiffness
matrix
K
G
R
mXm
j
s
given
by
and
the
load vector
F
e
R
m
by
The
boundary integral
in the
expression
for
Fi
is
zero unless
z»
is a
boundary
node.
(b)
The
compatibility condition
for
(C.5)
is
determined
by the
following
calcula-
tion:
(c)
Now
consider (C.5) with
where
O
is the
unit square.
We
will
produce
the finite
element solution using
the
regular grid with
18
triangles
(16
nodes).
The
stiffness
matrix
K
e
R
16x16
is
singular,
as
should
be
expected,
and
there
are
infinitely
many solutions.
The
Appendix
C.
Solutions
to
odd-numbered exercises
583
We will apply Galerkin's
method
with
Vm
equal
to
the
space of all continuous
piecewise linear function relative
to
a given triangulation
T.
We label
the
standard
basis of
Vm
as CPl,
CPz,
...
,
CPn,
and
the
nodes as
Zl,
Z2,
...
,
Zn.
(Every
node in
the
mesh is now free.)
Thus
Vn
= span { CPl,
CP2,
...
,
CPn}.
We
then
define
the
Galerkin approximation
Wn
by
Wn
E V
n
,
a(
Wn,
CPi)
=
(f,
CPi)
+ r
khcpi,
i =
1,2,
...
,m.
Jon
Writing
m
Wn
= L
(JjcPj
j=l
and
we
obtain
the
system
Kw
=
F.
The
stiffness
matrix
K E R
mxm
is given by
Kij =
a(cpj,CPi),
i,j
=
1,2,
...
,n,
and
the
load vector
FER
m by
Fi
=
(f,
cp;)
+ r
khcpi,
i = 1,2,
...
, n.
Jon
The
boundary
integral in
the
expression for
Fi
is zero unless
Zi
is a
boundary
node.
(b)
The
compatibility condition for
(C.5)
is determined
by
the
following calcula-
tion:
(c) Now consider
(C.5)
with
In
f = -
In
V·
(kVu)
__
r k
OU
-
Jon
an
= - r kh.
Jon
3 3xi
k(x)
= 1,
f(x)
=
XlXZ
+
4'
hex) =
-5'
where n
is
the
unit
square. We will produce
the
finite element solution using
the
regular grid with
18
triangles (16 nodes).
The
stiffness
matrix
K E
Rl6Xl6
is singular, as should
be
expected,
and
there
are infinitely
many
solutions.
The

584
Appendix
C.
Solutions
to
odd-numbered
exercises
Section
9.1
1.
The
complex Fourier series
of / is
where
CQ
= 2/3 and
The
errors
in
approximating
/ by a
partial Fourier series
are
shown
in
Figure
C.38.
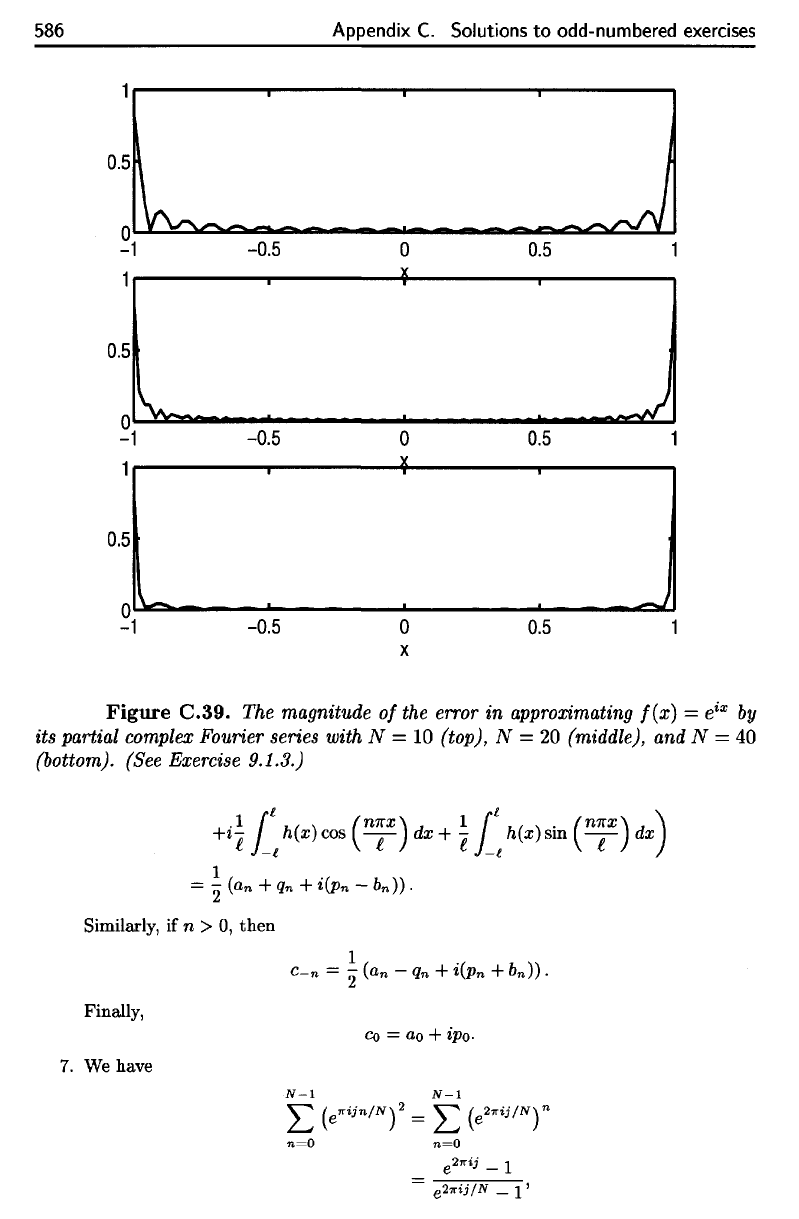
3.
The
complex Fourier
coefficients
of /
are
The
magnitudes
of the
error
in
approximating
/ by a
partial Fourier series
are
shown
in
Figure
C.39.
5.
Let
where
unique solution
u
with
last
component equal
to
zero
is
584
Appendix
C.
Solutions
to
odd-numbered exercises
unique solution u with last component equal
to
zero is
u=
0.3622
0.2984
0.1344
-0.0843
0.3728
0.3302
0.2081
0.0255
0.3803
0.3447
0.2334
0.0591
0.3665
0.3257
0.1878
0.0000
Section 9.1
1.
The
complex Fourier series of f is
00
n=-oo
where
Co
=
2/3
and
2(-1t
Cn
= - n
2
7r
2
'
n = ±1,
±2,
....
The
errors in approximating f
by
a partial Fourier series are shown in Figure C.38.
3.
The
complex Fourier coefficients of f are
(-It+
1
sin
(1)
C
n
=
n7r
-1
.
The
magnitudes of
the
error in approximating f
by
a partial Fourier series are shown
in Figure
C.39.
5.
Let
where
00
g(x)
=
ao
+ L (an cos
(n;x)
+ b
n
sin
(n;x))
,
n=l
ao
=
;£
Ii
g(x)dx,
-i
an
= l
!:
g(x)
cos
(n;x)
dx,
n =
1,2,3,
...
,
b
n
= l
Ii
g(x)
sin
(n;x)
dx,
n =
1,2,3,
...
,
-l

Appendix
C.
Solutions
to
odd-numbered
exercises
585
Figure
C.38.
The
error
in
approximating
f(x)
= 1
—
x
2
by its
partial
complex
Fourier series with
N = 10
(top),
N = 20
(middle),
and N = 40
(bottom).
(See
Exercise
9.1.1.)
(see
(6.25)),
and
similarly
let
The
complex Fourier
coefficient
of / is
given
by
For
n
> 0, we
have
Appendix
C.
Solutions
to
odd-numbered exercises
0.04r-------r-----r------r------,
-0.02
-0.04'-----
..........
----.&....----
..........
-------1
-1
-0.5 0
0.5
0.04r-----""T'"--------Il(~----..,..----.....,
0.02
Orvr-~--------------------------~~~vJ~
-0.02
-0.
04
'--
___
.........
___
--L
____
..........
___
....J
-1
-0.5 0
0.5
x_
0.04,......-----.r-------l.t-------,.-----..,
0.02
o~------------------------------------~
-0.02
-0.04'-------·
.....
----...I·~----
....
·-----~
-1
-0.5
o
x
0.5
585
Figure
C.38.
The error in approximating
f(x)
= 1 - x
2
by
its partial
complex Fourier series with N
= 10 (top), N = 20 (middle), and N = 40 (bottom).
(See Exercise 9.1.1.)
(see (6.25)),
and
similarly let
hex)
=
Po
+
f:
(Pn cos
(n;x)
+
qn
sin
(n;x))
.
n=l
The
complex Fourier coefficient
of!
is given
by
C
n
=
~
Ii
!(x)e-
i1rn
;r;/i
dx.
U
-i
For n >
0,
we have
Cn
=
2~
J:
(g(x)
+
ih(x))
(cos
(n;x)
-
isin
(n;x))
dx
1
(1
Ii
(n7rx)
.1
Ii
.
(n7rx)
="2
£
_£
g(x)
cos
-g-
dx
-
l£
-i
g(x)sm
-g-
dx
586
Appendix
C.
Solutions
to
odd-numbered exercises
Figure
C.39.
The
magnitude
of
the
error
in
approximating
f(x]
=
e
lx
by
its
partial complex Fourier series with
N = 10
(top),
N
=
20
(middle),
and N = 40
(bottom). (See Exercise
9.1.3.)
Similarly,
if n > 0,
then
Finally,
7.
We
have
586
0.5
o
"""-
-1 -0.5
0.5
o~
-1
-0.5
0.5
0-
-1
-0.5
Appendix
C.
Solutions
to
odd-numbered exercises
o
y
o
x
o
x
0.5
0.5
-
0.5
Figure
C.39.
The magnitude
of
the error in approximating
f(x)
= e
ix
by
its partial complex Fourier series with N = 10 (top), N = 20 (middle), and N = 40
(bottom). (See Exercise 9.1.3.)
+i
E
I:
h(x)
cos
(n;x)
dx
+ E
I:
h(x)
sin
(n;x)
dX)
=
~
(an +
qn
+
i(pn
- b
n
)).
Similarly, if n >
0,
then
Finally,
7.
We have
n=O
co
=
ao
+ ipo·
n=O
e
21rij
_
1
- e
21ri
j/N
-
l'

Appendix
C.
Solutions
to
odd-numbered
exercises
587
using
the
formula
for the sum of a finite
geometric series:
Moreover,
since
e
l6
is a
27r-periodic
function
of
9,
we see
that
e
27ry
= 1 and
hence
that
On
the
other hand,
by
Euler's
formula,
The
second equation
is one of the
results
we set out to
prove.
The first
equation
can be
written, using
the
trigonometric identity
sin
2
(9)
=
I
—
cos
2
(0),
as
Since
this expression equals
zero,
we
must have
which
simplifies
to
or
which
is the
desired result.
The
result
then
follows.
Appendix
C.
Solutions
to
odd-numbered exercises
587
using
the
formula for
the
sum
of a finite geometric series:
Moreover, since
e
i8
is a 27r-periodic function of 8,
we
see
that
e
27rij
= 1
and
hence
that
N-l
L
(e7rijn/N)2
=
O.
n=O
On
the
other
hand, by Euler's formula,
~
(;7rjn/N)2
~
(
(jn7r)
+
..
(jn7r))2
L...J
e =
L...J
cos N
~
sm N
n=O n=O
N-l
= L (cos
2
(j~7r)
_ sin
2
(j~7r)
+ 2icos
(j~7r)
sin
(j;))
n=O
=
y:
cos
2
e~7r)
-
y:
sin
2
e~7r)
n=O
n=O
N-l
+2i
L cos
(j~7r)
sin
(j~7r).
n=O
Since this expression equals zero,
we
must have
y:
cos
2
e~7r)
-
y:
sin
2
e~7r)
=
0,
n=O n=O
N-l
L cos
(j~7r)
sin
(j~7r)
=
O.
n=O
The
second equation is one of
the
results
we
set
out
to
prove.
The
first equation
can
be
written, using
the
trigonometric identity sin
2
(8) = 1 - cos
2
(8),
as
y:
cos
2
e~7r)
- £
(1
-cos
2
e~7r))
=
0,
n=O n=O
which simplifies
to
N-l
2 L cos
2
e~7r)
=
N,
n=O
or
~COS2
e~7r)
N
-"2'
n=O
which is
the
desired result.
The
result
~
sin
2
e~7r)
=
~
n=O
then
follows.
