Gockenbach M.S. Partial Differential Equations. Analytical and Numerical Methods
Подождите немного. Документ загружается.


388
Chapter
8.
Problems
in
multiple spatial dimensions
8.4.4 Finite elements
and
Neumann conditions
We
will close
by
describing
briefly
how
Neumann conditions
are
handled
in
two-
dimensional
finite
elements.
For the
sake
of
generality,
we
will
consider
a
problem
with possibly mixed boundary conditions.
So
suppose
£7
is a
domain
in
either
R
2
or
R
3
, and
assume
that
dtl
has
been partitioned into
two
disjoint sets:
d£l
=
I\
LJ
T^.
We
consider
the
following
BVP:
As
we
discussed
in
Section 6.5, Dirichlet conditions
are
termed essential boundary
conditions because they must
be
explicitly imposed
in the finite
element method,
while
Neumann conditions
are
called natural
and
need
not be
mentioned.
We
therefore
define
the
space
of
test
functions
by
The
weak
form
of
(8.59)
is now
derived exactly
as on
page 378;
the
boundary
integral
now
vanishes because
v = 0 on
FI
and
du/dn
— 0 on
F
2
.
Thus
the
weak
form
of
(8.59)
is:
The
bilinear
form
a(-,
•) is
defined exactly
as
before (the only
difference
from
(8.53)
is
in the
space
of
test
functions).
We
now
restrict
our
discussion once more
to
two-dimensional polygonal
do-
mains.
To
apply
the finite
element method,
we
must choose
an
approximating
subspace
of
V.
Since
the
boundary conditions
are
mixed,
there
are at
least
two
points where
the
boundary conditions change
from
Dirichlet
to
Neumann.
We
will
make
the
assumption
that
the
mesh
is
chosen
so
that
all
such
points
are
nodes (and
that
all
such nodes belong
to
F
1;
that
is,
that
FI
includes
its
"endpoints").
We can
then choose
the
approximating subspace
of V as
follows:
A
basis
for
V
n
is
formed
by
including
all
basis
functions
corresponding
to
interior
nodes
(as in the
Dirichlet case),
as
well
as the
basis
functions
corresponding
to
boundary nodes
that
do not
belong
to
FI.
For an
example
of a
basis
function
corresponding
to a
boundary node,
see
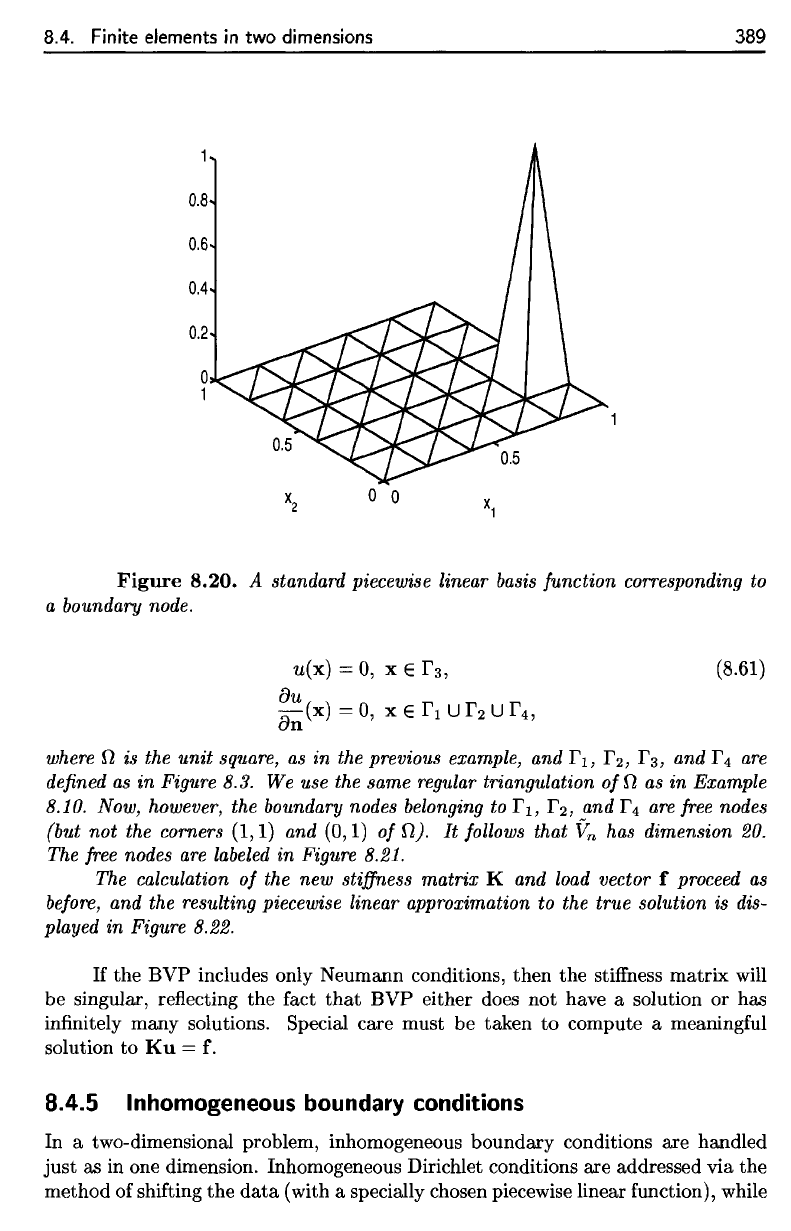
Figure 8.20.
Example
8.11.
We
consider
the BVP
388
Chapter
8.
Problems
in
multiple spatial dimensions
8.4.4
Finite elements and Neumann conditions
We
will close by describing briefly how Neumann conditions are handled in two-
dimensional finite elements. For
the
sake of generality,
we
will consider a problem
with possibly mixed boundary conditions.
So
suppose n
is
a domain in either R2 or
R3, and assume
that
an
has been partitioned into two disjoint sets:
an
= r
1
ur
2
.
We
consider the following BVP:
-\7
. (k(x)\7u) =
I(x),
x E
n,
u(x) = 0, x E r
1
,
au
an
(x) = 0, x E r2 .
(8.59)
As
we
discussed in Section 6.5, Dirichlet conditions are termed essential boundary
conditions because they must be explicitly imposed in the finite element method,
while Neumann conditions are called
natural
and
need not be mentioned.
We
therefore define the space of test functions by
v = {u E C
2
(O)
: u(x) =
O,X
E
rt}.
The weak form of
(8.59)
is
now derived exactly as on page
378;
the
boundary
integral
r
k(X)V
a
au
= r
k(X)V
a
au
+ r k(x)V
a
au
Jon
n
Jrl
n
Jr2
n
now vanishes because v = 0 on r
1
and
au/an
= 0 on r
2
.
Thus
the
weak form of
(8.59)
is:
Find u E V such
that
a(u,
v)
=
(f,
v)
for all v E
V.
(8.60)
The bilinear form
a(·,·)
is
defined exactly as before (the only difference from
(8.53)
is
in the space of test functions).
We
now restrict our discussion once more to two-dimensional polygonal do-
mains.
To
apply
the
finite element method,
we
must choose an approximating
subspace of
V.
Since
the
boundary conditions are mixed, there are
at
least two
points where the boundary conditions change from Dirichlet
to
Neumann.
We
will
make the assumption
that
the mesh
is
chosen
so
that
all such points are nodes (and
that
all such nodes belong to r
1
,
that
is,
that
r
1
includes its "endpoints").
We
can
then choose
the
approximating subspace of V as follows:
Vn
= {v E C(O') : v
is
piecewise linear on
/,
v(z) = 0 for all nodes z E
rt}.
A basis for
Vn
is formed by including all basis functions corresponding
to
interior
nodes (as in the Dirichlet case), as
well
as the basis functions corresponding
to
boundary nodes
that
do not belong
to
r
1.
For an example of a basis function
corresponding to a boundary node, see Figure 8.20.
Example
8.11.
We
consider the
BVP
-~U=X1,
xEn,
8.4.
Finite
elements
in two
dimensions
389
Figure
8.20.
A
standard
piecewise linear
basis
function
corresponding
to
a
boundary
node.
u(x)
= 0, x €
T
3
,
du
—(x)
= o,
xeriur
2
ur
4
,
an
(8.61)
where
Jl
is the
unit square,
as in the
previous example,
and
TI,
1^,
T$,
and
T±
are
defined
as in
Figure
8.3.
We use the
same
regular
triangulation
of ft, 05 in
Example
8.10.
Now, however,
the
boundary
nodes
belonging
to
TI,
r
2
,
and
F
4
are
free
nodes
(but
not the
corners
(1,1)
and
(0,1)
of
Ci).
It
follows
that
V
n
has
dimension
20.
The
free
nodes
are
labeled
in
Figure
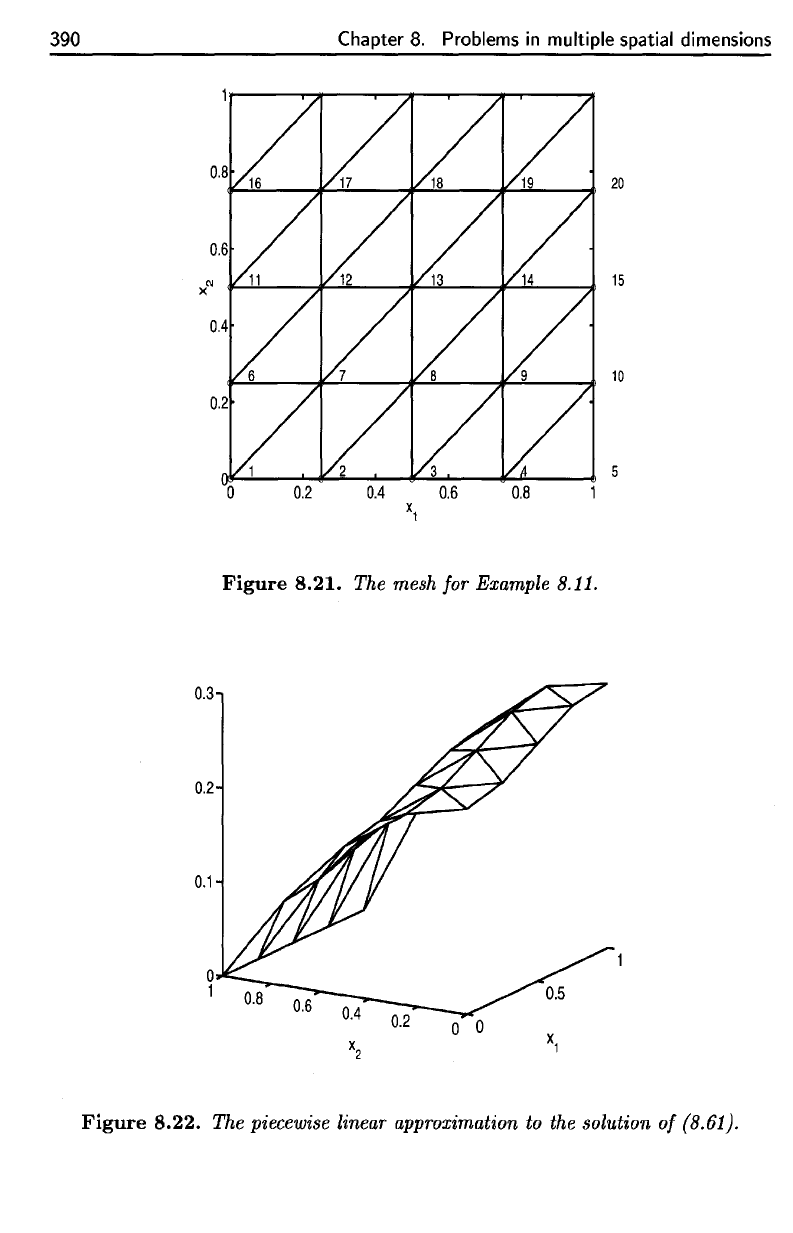
8.21.
The
calculation
of the new
stiffness
matrix
K and
load
vector
f
proceed
as
before,
and the
resulting piecewise linear approximation
to the
true solution
is
dis-
played
in
Figure
8.22.
If
the BVP
includes only Neumann conditions, then
the
stiffness
matrix
will
be
singular, reflecting
the
fact
that
BVP
either
does
not
have
a
solution
or has
infinitely
many solutions. Special care must
be
taken
to
compute
a
meaningful
solution
to Ku =
f.
8.4.5
Inhomogeneous
boundary
conditions
In a
two-dimensional problem, inhomogeneous boundary conditions
are
handled
just
as in one
dimension. Inhomogeneous Dirichlet conditions
are
addressed
via the
method
of
shifting
the
data
(with
a
specially chosen piecewise linear
function),
while
8.4. Finite elements
in
two dimensions
0.8
0.6
0.4
0.2
o
1
o 0
389
Figure
8.20.
A standard piecewise linear basis function corresponding to
a boundary node.
u(x)
= 0, x E r
3
,
au
an
(x) = 0, x E r
l
U r
2
U r
4
,
(8.61)
where 0 is the
unit
square,
as
in the previous example, and
fl'
r
2
, r
3
, and r
4
are
defined
as
in Figure 8.3. We use the same regular triangulation
of
0
as
in
Example
8.10. Now, however, the boundary nodes belonging to r
l
,
r
2
,
and r
4
are
free nodes
(but
not
the corners (1,1) and (0,1)
of
OJ.
It
follows that
Vn
has dimension 20.
The free nodes
are
labeled in Figure 8.21.
The calculation
of
the new stiffness matrix K and load vector f proceed
as
before, and the resulting piecewise linear approximation to the true solution is dis-
played
in
Figure 8.22.
If
the BVP includes only Neumann conditions, then
the
stiffness matrix will
be singular, reflecting the fact
that
BVP either does not have a solution or has
infinitely many solutions. Special care must be taken
to
compute a meaningful
solution to
Ku
= f.
8.4.5 Inhomogeneous boundary conditions
In a two-dimensional problem, inhomogeneous boundary conditions are handled
just
as in one dimension. Inhomogeneous Dirichlet conditions are addressed via
the
method of shifting the
data
(with a specially chosen piecewise linear function), while
390
Chapter
8.
Problems
in
multiple spatial dimensions
Figure
8.21.
The
mesh
for
Example 8.11.
Figure
8.22.
The
piecewise linear approximation
to the
solution
of
(8.61).
390
0.3
0.2
0.1
o
1
Chapter
8.
Problems
in
multiple
spatial
dimensions
20
15
10
Figure
8.21.
The mesh for Example 8.11.
Figure
8.22.
The piecewise linear approximation to the solution
of
(8.61).

8.4.
Finite
elements
in two
dimensions
391
inhomogeneous
Neumann conditions
are
taken into account directly when deriving
the
weak
form.
Both types
of
boundary conditions lead
to a
change
in the
load
vector. Exercises
5 and 7 ask the
reader
to
derive
the
load vectors
in
these cases.
Exercises
1.
Consider
the BVP
where
£)
is the
unit square,
k(x)
=
I
+
x\x^
and
/(x)
= 1.
Produce
the
piecewise
linear
finite
element (approximate) solution using
a
regular grid
with
18
triangles.
2.
Repeat Exercise
1,
but
suppose
that
the
boundary conditions
are
homogeneous
Neumann
conditions
on the
right side
F
2
of the
square
and
homogeneous
Dirichlet conditions
on the
other
three
sides.
3.
Repeat Exercise
1, but
suppose
that
the
boundary conditions
are
homogeneous
Neumann
conditions
on
every
part
of the
boundary
of
fi.
Let the
right-hand
side
be
/(x)
=
#1
—
1/2 (so
that
the
compatibility condition
is
satisfied
and
a
solution
exists).
4.
If u
does
not
belong
to
V
n
,
then
is
not
equal
to u.
Instead,
w
is the
piecewise linear interpolant
of u
(relative
to
the
given mesh
T).
The
interpolant
of u is one
piecewise linear approximation
to u] if u is the
solution
to a
BVP, then
the finite
element method computes
another.
The
purpose
of
this
exercise
is to
compare
the
two.
(a)
Verify
that
w(x)
=
#1X2(1
—
#i)(l
—
#2)
is the
solution
to the
Dirichlet
problem
where
fi is the
unit
square.
(b)
Let T be the
regular
triangulation
of
£)
with
18
triangles. Compute
the
finite
element
approximation
to u
using piecewise linear
functions
on T.
(c)
Compute
the
piecewise linear
interpolant
of u
relative
to T.
(d)
Which
is a
better approximation
of u, the finite
element approximation
or
the
interpolant?
Justify
your answer both theoretically
and
numerically.
8.4. Finite elements
in
two dimensions
391
inhomogeneous Neumann conditions are taken into account directly when deriving
the weak form. Both types of boundary conditions lead to a change in
the
load
vector. Exercises 5 and 7 ask the reader
to
derive the load vectors in these cases.
Exercises
1.
Consider the
BVP
-V'.
(k(x)V'u) =
I(x),
x
EO,
u(x)
=
0,
x E
a~,
where 0
is
the
unit square, k(x) = 1 +
X1X2
and
I(x)
=
1.
Produce the
piecewise linear finite element (approximate) solution using a regular grid
with
18
triangles.
2.
Repeat Exercise
1,
but
suppose
that
the boundary conditions are homogeneous
Neumann conditions on the right side
f2
of the square and homogeneous
Dirichlet conditions on
the
other three sides.
3.
Repeat Exercise
1,
but
suppose
that
the boundary conditions are homogeneous
Neumann conditions on every
part
of the boundary of
O.
Let
the
right-hand
side be
I(x)
=
Xl
-
1/2
(so
that
the compatibility condition
is
satisfied and
a solution exists).
4.
If
U does not belong to V
n
,
then
n
W =
LU(Zi)¢i
i=l
is
not equal to
u.
Instead, w
is
the piecewise linear interpolant of U (relative
to
the given mesh T). The interpolant of U
is
one piecewise linear approximation
to
U;
if U
is
the
solution
to
a BVP, then
the
finite element method computes
another. The purpose of this exercise
is
to compare
the
two.
(a) Verify
that
u(x)
=
X1X2(1
-
xd(1
-
X2)
is
the solution
to
the
Dirichlet
problem
-6.u
= 2Xl(1 - Xl) + 2x2(1 -
X2),
x E fl,
u(x)
= 0, x E
a~,
where 0
is
the unit square.
(b) Let
T be the regular triangulation of 0 with
18
triangles. Compute
the
finite element approximation
to
u using piecewise linear functions on T.
(c)
Compute
the
piecewise linear interpolant of u relative
to
T.
(d) Which
is
a
better
approximation of
u,
the finite element approximation or
the
interpolant? Justify your answer
both
theoretically
and
numerically.

392
Chapter
8.
Problems
in
multiple
spatial dimensions
5.
(a)
Explain
how to
solve
an
inhomogeneous Dirichlet problem using piece-
wise
linear
finite
elements.
(b)
Illustrate
the
procedure
on the
following
BVP:
Let
J7
be the
unit square
and use a
regular grid with
18
triangles.
6.
Suppose
u is a
solution
to
(8.53). Prove
that
u
also solves (8.52).
7.
(a)
Explain
how to
solve
an
inhomogeneous Neumann problem using piece-
wise
linear
finite
elements.
(b)
What
is the
compatibility condition
for an
inhomogeneous Neumann
problem?
(c)
Illustrate
the
procedure
on the
following
BVP:
Let
fi
be the
unit square
and use a
regular grid with
18
triangles.
8.5
Suggestions
for
further
reading
The
foundation
of
PDEs
in two or
more
spatial
dimensions
is
advanced calculus.
Kaplan [29] gives
a
straightforward introduction;
an
alternative
at the
same level
is
Greenberg
[20].
A
more advanced
treatment
can be
found
in
Marsden
and
Tromba
[37].
All
of the
references cited
in
Sections
5.8 and 6.7
deal with PDEs
in
multiple
spatial
dimensions. Another source
of
information
about
Bessel function
is
Folland
[15].
392 Chapter
8.
Problems
in
multiple spatial dimensions
5.
(a) Explain how to solve an inhomogeneous Dirichlet problem using piece-
wise linear finite elements.
(b) Illustrate the procedure on
the
following BVP:
-~u
= 0 in
0,
u(x)
= xi, x E
a~.
Let 0 be the unit square
and
use a regular grid with
18
triangles.
6.
Suppose u
is
a solution
to
(8.53). Prove
that
u also solves (8.52).
7.
(a) Explain how
to
solve an inhomogeneous Neumann problem using piece-
wise linear finite elements.
(b)
What
is the compatibility condition for
an
inhomogeneous Neumann
problem?
(c)
Illustrate the procedure on
the
following BVP:
-~u
=
X1X2
+
~
in
0,
au
3xi
an(x)
=
-5'
x E
a~.
Let 0 be the unit square and use a regular grid with
18
triangles.
8.5 Suggestions for further reading
The foundation of PDEs in two or more spatial dimensions
is
advanced calculus.
Kaplan
[29]
gives a straightforward introduction;
an
alternative
at
the same level
is
Greenberg
[20].
A more advanced treatment can be found in Marsden and 'Tromba
[37].
All
of the references cited in Sections 5.8
and
6.7 deal with PDEs in multiple
spatial dimensions. Another source of information about Bessel function
is
Folland
[15].

In the
preceding chapters,
we
introduced several kinds
of
Fourier series:
the
Fourier
sine
series, cosine series, quarter-wave sine series, quarter-wave cosine series,
and
the
full
Fourier series. These series were primarily used
to
represent
the
solution
to
differential
equations,
and
their
usefulness
was
based
on two
facts:
1.
Each
is
based
on an
orthogonal sequence with
the
property
that
every con-
tinuous function
can be
represented
in
terms
of
this
sequence.
2.
The
terms
in the
series represent
eigenfunctions
of
certain simple
differential
operators (under various boundary conditions). This accounts
for the
fact
that
it is
computationally tractable
to
determine
a
series representation
of
the
solution
to the
corresponding
differential
equation.
In
this chapter
we
will
go
deeper into
the
study
of
Fourier series.
Specifically,
we
will
consider
the
following
questions:
1.
What
is the
relationship among
the
various kinds
of
Fourier series?
2.
How can a
partial
Fourier series
be
found
and
evaluated
efficiently?
3.
Under what conditions
and in
what sense
can a
function
be
represented
by its
Fourier
series?
4.
Can the
Fourier series method
be
generalized
to
more complicated
differential
equations (including nonconstant
coefficients
and/or
irregular
geometry)?
Our
discussion
will
justify
many
of the
statements
we
made earlier
in the
book
concerning
the
convergence
of
Fourier series.
It
also introduces
the
fast
Fourier
transform
(FFT), which
is an
exciting
and
recent development
(from
the
last
half
of
the
twentieth
century
63
)
in the
long history
of
Fourier series.
The
calculation
of
N
Fourier
coefficients
would appear
to
require
O(JV
2
)
operations (for reasons
that
63
The
FFT was
popularized
in the
1960s,
by the
paper
[12].
However,
the
method
was
known
to
Gauss long before;
see
[25].
393
Chapter
9
Mope
about Fourier
series
f.+~
,
iI
?!
r
i
~
'
~I¢.
~
~
bout
Fourier series
In the preceding chapters,
we
introduced several kinds of Fourier series: the Fourier
sine series, cosine series, quarter-wave sine series, quarter-wave cosine series, and
the
full Fourier series. These series were primarily used to represent the solution
to
differential equations, and their usefulness was based on two facts:
1.
Each
is
based on an orthogonal sequence with
the
property
that
every con-
tinuous function can be represented in terms of this sequence.
2.
The terms in the series represent eigenfunctions of certain simple differential
operators (under various boundary conditions). This accounts for the fact
that
it
is
computationally tractable to determine a series representation of
the solution
to
the corresponding differential equation.
In this chapter
we
will go deeper into
the
study of Fourier series. Specifically,
we
will consider the following questions:
1.
What
is
the relationship among the various kinds of Fourier series?
2.
How can a partial Fourier series be found
and
evaluated efficiently?
3.
Under what conditions and in what sense can a function be represented by its
Fourier series?
4.
Can the Fourier series method be generalized to more complicated differential
equations (including nonconstant coefficients
and/or
irregular geometry)?
Our discussion will justify many of the statements
we
made earlier in
the
book
concerning the convergence of Fourier series.
It
also introduces
the
fast Fourier
transform (FFT), which
is
an
exciting and recent development (from the last half
of the twentieth century
63) in the long history of Fourier series. The calculation of
N Fourier coefficients would appear
to
require O(N2) operations (for reasons
that
63The
FFT
was
popularized
in
the
1960s,
by
the
paper
[12]. However,
the
method
was known
to
Gauss
long before; see [25].
393

we
see
that
394
Chapter
9.
More about Fourier
series
we
explain
in
Section 9.2).
The FFT
reduces
the
operation count
to
O(NlogN),
a
considerable savings when
TV
is
large.
We
begin
by
introducing
yet
another
type
of
Fourier
series,
the
complex
Fourier series,
that
is
convenient both
for
analysis
and for
expressing
the
FFT.
9.1 The
complex Fourier
series
We
saw in
Chapter
4
that
problems apparently involving only real numbers
can
sometimes
be
best addressed with techniques
that
use
complex numbers.
For ex-
ample,
if the
characteristic roots
r\
and
r-2
of the ODE
are
distinct,
then
the
general solution
is
This formula holds even
if
r\
and
r%
are
complex,
in
which case
u is
complex-valued
for
most choices
of
c\
and
c^.
(We
also saw,
in
Section 4.2.1,
how to
recover
the
general
real-valued
solution
if
desired.)
In
a
similar way, there
are
some advantages
to
using
complex-valued
eigenfunc-
tions, even when solving
differential
equations involving only
real-valued
functions.
Using
Euler's
formula,
and
therefore
This
suggests
that
the
negative second derivative operator
has
complex exponential
eigenfunctions.
We
leave
it to the
exercises (see Exercise
4) to
show
that
nonzero solutions
to
the BVP
394
Chapter 9. More
about
Fourier series
we
explain in Section 9.2).
The
FFT
reduces
the
operation count
to
O(NlogN),
a
considerable savings when N
is
large.
We begin
by
introducing yet
another
type
of Fourier series,
the
complex
Fourier series,
that
is
convenient
both
for analysis
and
for expressing
the
FFT.
9.1
The
complex Fourier
series
We saw in
Chapter
4
that
problems
apparently
involving only real numbers can
sometimes
be
best addressed with techniques
that
use complex numbers. For ex-
ample, if
the
characteristic roots
rl
and
r2
of
the
ODE
rPu du
a dt
2
+ b dt + cu = 0
are distinct,
then
the
general solution is
u(t) =
Cl
e
Tlt
+
c2e
T2t
•
This formula holds even
if
rl
and
r2
are complex, in which case u is complex-valued
for most choices of
Cl
and
C2.
(We also saw, in Section 4.2.1, how
to
recover
the
general real-valued solution
if
desired.)
In a similar way, there
are
some advantages
to
using complex-valued eigenfunc-
tions, even when solving differential equations involving only real-valued functions.
Using Euler's formula,
we see
that
and
therefore
e
iO
= cos e + i sin
e,
d~
[eiW<V]
= !
[cos
(wx) + i sin
(wx)]
=
-wsin
(wx) + iwcos (wx)
=
iw
(cos (wx) + i sin (wx))
=
iweiw<v,
d
2
[,]
2'
__
e'wx
=
-(iw)
e'wx
dx
2
This suggests
that
the
negative second derivative
operator
has complex exponential
eigenfunctions.
We
leave
it
to
the
exercises (see Exercise
4)
to
show
that
nonzero solutions
to
the
BVP
rPu
- dx
2
=
AU,
-£
< x <
£,
u(
-f)
= u(£),
(9.1)
du (_£) = du
(£),
dx dx

9.1.
The
complex
Fourier
series
395
exist only
for A =
0,7r
2
/7
2
,...,
n
2
?r
2
/£
2
,
— The
eigenvalue
A = 0 has
eigenfunc-
tion
1
(the
constant
function),
while each eigenvalue
A =
n
2
ir
2
/I
2
has two
linearly
independent
eigenfunctions,
When
n = 0,
e™
nx
/
1
reduces
to the
constant
function
1 and A =
n
2
?r
2
/7
2
reduces
to A
=
0.
Therefore,
to
simplify
the
notation,
we
will write
the
complete list
of
eigenvalue-eigenfunction
pairs
as
In
this section
we use the
eigenfunctions given
in
(9.2)
to
form
Fourier series
representing
functions
on the
interval
(—£,(.).
Since Fourier series calculations
are
based
on
orthogonality,
we
must take
a
slight detour
to
discuss complex vector space
and
inner products. Some
of the
following
results have been used earlier
in the
text,
but
only
briefly
in the
course
of
demonstrating
that
a
symmetric operator
has
only
real
eigenvalues.
9.1.1
Complex
inner
products
As
we
discussed
in
Section 3.1,
a
vector space
is a set of
objects (vectors), along
with
two
operations, (vector) addition
and
scalar multiplication.
To
this point,
we
have used real numbers
as the
scalars;
however,
the
complex numbers
can
also
be
used
as
scalars.
For
emphasis, when
we use
complex numbers
as
scalars,
we
refer
to the
vector space
as a
complex
vector
space.
The
most common complex vector space
is
C
n
,
complex
n-space:
Just
as for
R
n
,
addition
and
scalar multiplication
are
defined
componentwise.
The
only adjustment
that
must
be
made
in
working with complex vector
spaces
is in the
definition
of
inner
product.
If
u
is a
vector
from
a
complex vector
space, then
it is
permissible
to
multiply
u by the
imaginary unit
i to get iu. But if
there
is an
inner product
(•, •) on the
space,
and if the
familiar properties
of
inner
product hold, then
This suggests
that
either
(w,u)
or
(iu,iu)
is
negative, contradicting
one of the
rules
of
inner products (and making
it
impossible
to
define
a
norm based
on the
inner
product).
For
this
reason,
the
definition
of
inner product
is
modified
for
complex vector
spaces.
9.1. The complex Fourier
series
395
exist only for A =
0,
1f2
/£2,
...
,n
2
7r
2
/£2, . ...
The
eigenvalue A = 0 has eigenfunc-
tion 1 (the constant function), while each eigenvalue
A = n
2
7r
2
/£2
has two linearly
independent eigenfunctions,
When
n = 0,
ei7fnx/l
reduces to the constant function 1 and A = n
2
1f2/£2
reduces
to
A =
O.
Therefore,
to
simplify the notation,
we
will write
the
complete list of
eigenvalue-eigenfunction pairs as
2 2
n
1f
i7fnx/l
0 1
±2
T,e
,n=
,±,
,
....
(9.2)
In
this section
we
use
the
eigenfunctions given in (9.2)
to
form Fourier series
representing functions on
the
interval
(-£,
f). Since Fourier series calculations are
based on orthogonality,
we
must take a slight detour
to
discuss complex vector space
and
inner products. Some of the following results have been used earlier in the text,
but
only briefly in
the
course of demonstrating
that
a symmetric operator has only
real eigenvalues.
9.1.1 Complex inner products
As
we
discussed in Section 3.1, a vector space
is
a set of objects (vectors), along
with two operations, (vector) addition and scalar multiplication. To this point,
we
have used real numbers as the scalars; however, the complex numbers can also be
used as scalars. For emphasis, when
we
use complex numbers as scalars,
we
refer
to
the vector space as a complex vector space.
The
most common complex vector space
is
en,
complex n-space:
Just
as for R
n
,
addition and scalar multiplication are defined componentwise.
The
only adjustment
that
must be made in working with complex vector
spaces is in the definition of inner product.
If
u
is
a vector from a complex vector
space, then
it
is
permissible
to
multiply u by the imaginary unit i
to
get iu.
But
if
there
is
an
inner product (.,.) on
the
space, and if
the
familiar properties of inner
product hold, then
(iu,iu) = i2(u,U) =
-(u,u).
This suggests
that
either (u,u) or (iu,iu)
is
negative, contradicting one
of
the rules
of inner products (and making
it
impossible
to
define a norm based on the inner
product).
For this reason, the definition of inner product is modified for complex vector
spaces.

Definition
9.1.
Let V be a
complex
vector
space.
An
inner product
on V is a
function taking
two
vectors from
V and
producing
a
complex
number,
in
such
a way
that
the
following
three
properties
are
satisfied:
1.
(w,t>)
=
(v,u)
for all
vectors
u and v;
2.
(au
+
j3v,
w]
—
a(u,
w)
+
{3(v,
w)
and
(w,
au
+ fiv) —
a(w,
u) + fi(w, v) for all
vectors
u,
v,
and w and all
complex
numbers
a and 0;
3. (w,
w)
>
0 for all
vectors
u,
and
(u,u)
— 0 if and
only
if
u is the
zero
vector.
In
the
above
definition,
z
denotes
the
complex conjugate
of z € C. (If z =
x +
iy,
with
x,
y € R,
then
~z
= x
—
iy.)
For
C
n
,
the
inner product
is
suggested
by the
fact
that
(We
will
use the
same notation
as for the
real
L
2
inner product, since,
when
/ and g
are
real-valued,
the
presence
of the
complex conjugate
in the
formula
has no
effect,
and the
ordinary
L
2
inner product
is
obtained.)
9.1.2 Orthogonality
of the
complex exponentials
A
direct calculation
now
shows
that
the
eigenfunctions
given
in
(9.2)
are
orthogonal
with
respect
to the
(complex)
L
2
inner product:
396
Chapter
9.
More about Fourier
series
for
z € C. We
define
It is
straightforward
to
verify
that
the
properties
of an
inner product
are
satisfied.
In
particular,
If
we now
consider
the
space
of
complex-valued
functions defined
on an
interval
[a,
b],
the
same reasoning
as in
Section
3.4
leads
to the
complex
L
2
inner product,
396
Chapter 9. More about Fourier series
Definition
9.1.
Let V
be
a complex vector
space.
An
inner product
on
V is a
function taking
two
vectors from V and producing a complex number, in such a way
that the following three properties
are
satisfied:
1.
(u,V) = (v,u) for
all
vectors u and
V;
2.
(au +
/3v,
w)
= a(u,
w)
+
/3(v,
w)
and
(w,
au
+
/3v)
= a(w, u) +
73(w,
v)
for
all
vectors u, v, and
wand
all
complex numbers
0:
and
/3;
3.
(u,u)
2:
0 for
all
vectors u, and (u,u) = 0
if
and only
ifu
is
the
zero
vector.
In
the
above definition, z denotes
the
complex conjugate
of
z E
C.
(If z =
x + iy, with
x,y
E
R,
then
z = x - iy.)
For C
n
,
the
inner
product
is suggested by
the
fact
that
for z E
C.
We
define
IZI=#
n
(U,V)cn
=
U·
V = L UiVi·
j=1
It
is straightforward
to
verify
that
the
properties of
an
inner
product
are satisfied.
In particular,
n
(u,u)c
n
=
LUi'lli
j=1
n
= L
IUil
2
2:
O.
j=1
If we now consider
the
space
of
complex-valued functions defined
on
an
interval
[a,
bj,
the
same reasoning as in Section 3.4 leads
to
the
complex
L2
inner product,
(J,g) = i
b
f(x)g(x) dx.
(We will use
the
same
notation
as for
the
real
L2
inner product, since, when f
and
9
are
real-valued,
the
presence of
the
complex conjugate
in
the
formula
has
no effect,
and
the
ordinary
L2
inner
product
is obtained.)
9.1.2 Orthogonality of the complex exponentials
A direct calculation now shows
that
the
eigenfunctions given in (9.2) are orthogonal
with respect
to
the
(complex)
L2
inner product:
(ei1fnX/t, em1fix/i) =
rt
ei1fnx/£e-m1fix/£ dx
i-I

This
shows
that
the
L
2
norm
of the
eigenfunction
is
y/%1.
9.1.3 Representing functions with complex Fourier
series
If
/ is a
continuous,
complex-valued
function
denned
on
[—I,I],
then
its
complex
Fourier
series
is
9.1.
The
complex
Fourier
series
397
The
last
step
follows
because
e^
n
m
^
1
is
27r-periodic.
We
also have
where
These
complex
Fourier
coefficients
are
computed according
to the
projection theo-
rem;
it
follows
that
is
the
element
of the
subspace
closest
to / in the
L
2
norm. Also,
we
will
show
in
Section
9.6
that
the
complex
Fourier series converges
to / in the L
2
norm under mild conditions
on / (in
partic-
ular,
if / is
continuous).
9.1. The complex Fourier
series
=
1£
e(n-m)1rix/£
dx
-£
=
[e(n-m)1rix/£
] £
(n
- m)7ri/C
_£
= C
(e(n-m)1Ti
_
e-(n-m)1Ti)
(n - m)7ri
=
0,
m
f.
n.
The
last step follows because
e(n-m)Oi
is
27r-periodic.
We
also have
(ei1TnX/l,ei1rnX/l)
=
1£
ei1rnx/fe-i1Tnx/fdx
-l
=
1£
dx
-£
=
2£.
This shows
that
the
L2
norm of
the
eigenfunction is
VU.
9.1.3 Representing functions with complex Fourier
series
397
If
f
is
a continuous, complex-valued function defined on [-C,
C],
then
its complex
Fourier series
is
where
CXl
'""'
c e
i1Tnx
/£
~
n ,
n=-CXl
1
1f
.
=
2C
f(x)e-'1rnx/£
dx.
-£
These complex Fourier coefficients are computed according
to
the
projection theo-
rem;
it
follows
that
is
the
element of
the
subspace
N
L cnei1Tnx/£
n=-N
span
{e
-i1rNX/£
e-i1r(N-l)x/£
e-
i1rx
/
L
1 e
i1rx
/
l
ei1rNX/L}
, , ... ,
",
.. "'
closest
to
f in
the
L2
norm. Also,
we
will show in Section 9.6
that
the
complex
Fourier series converges
to
f in
the
L2
norm under mild conditions on f (in partic-
ular, if
f is continuous).
