Gockenbach M.S. Partial Differential Equations. Analytical and Numerical Methods
Подождите немного. Документ загружается.


57
These
estimates were computed
in
Mathematica,
using
the
BesselJ
function
and the
Find-
Root
command.
368
Chapter
8.
Problems
in
multiple spatial dimensions
by
making
the
change
of
variables
s =
or.
The
result
is
with
the
last
step
following
from
the
assumption
that
J
n
(o:a)
= 0.
Finally,
applying (8.41),
we
obtain
(8.42).
4.
Each
J
n
,
n
=
0,1,2,...,
has an
infinite
number
of
positive roots, which
we
label
s
n
i
<
s
n
2
<
s
n
3
< • •
••
(There
is no
simple formula
for the
roots
s
nm
.)
We
will
not
prove
this
fact. Figure 8.10 shows
the
graphs
of
Jo,
Ji,
and
J^.
For
future
reference,
we
give here some
of the
roots
57
of the
Bessel functions:
8.3.5
The
eigenfunctions
of the
negative
Laplacian
on the
disk
Since
J
n
has an
infinite
sequence
of
positive roots, there
are
infinitely many positive
solutions
to
namely,
Therefore,
for
each value
of
n,
n
=
0,l,2,...,
there
are
infinitely many solutions
to
(8.32).
For
each value
of n,
there
are two
independent solutions
to
(8.31):
368
Chapter
8.
Problems
in
multiple spatial dimensions
by making the change of variables 8 =
aT.
The result is
with
the
last step following from
the
assumption
that
In(aa) =
O.
Finally,
applying (8.41),
we
obtain (8.42).
4.
Each I
n
,
n =
0,1,2,
...
, has an infinite number of positive roots, which
we
label 8
n
1 < 8
n
2 < 8
n
3 < .... (There is no simple formula for the roots 8
nm
.)
We
will not prove this fact. Figure 8.10 shows the graphs of
Jo,
J
1
, and
J2.
For future reference,
we
give here some of the roots
57
of the Bessel functions:
80m
= 2.404825557690968,5.520078109856846,
8.65372791291017,11. 79153381314112,
...
,
81m
= 3.831704472655219,7.015586669057602,
10.17346813505608,13.32368935305259,
...
, (8.43)
82m
= 5.135622247449045,8.41724413443633,
11.61984117182147,14.79595178232688,
...
,
83m
= 6.380161894536216,9.76102306245301,
13.01520072163691,16.22346616026436,
....
8.3.5 The eigenfunctions
of
the negative laplacian on the
disk
Since I
n
has an infinite sequence of positive roots, there are infinitely many positive
solutions to
namely,
2
\
snm
Amn
=
A2
' m =
1,2,3,
....
Therefore, for each value of n, n =
0,1,2,
...
, there are infinitely many solutions
to
(8.32). For each value of
n,
there are two independent solutions
to
(8.31):
cos
(nO),
sin
(nO).
57These
estimates
were
computed
in
Mathematica, using
the
BesselJ
function
and
the
Find-
Root
command.

8.3. Fourier
series
on a
disk
369
Figure
8.10.
The
Bess
el
function
JQ,
3\,
and
J^.
We
therefore
obtain
the
following
doubly indexed sequence
of
eigenvalues
for
—
A
p
(on
the
disk
and
under Dirichlet conditions), with
one or two
independent eigen-
functions
for
each eigenvalue:
Since
—
A
p
is
symmetric under Dirichlet conditions,
we
know
that
eigenfunctions
corresponding
to
distinct eigenvalues
are
orthogonal.
It
turns
out
that
(pmn
an
d
/2"\
(Pmn
are
orthogonal
to
each other
as
well,
as a
direct calculation shows:
8.3. Fourier
series
on
a disk
0.5
-
y=Jox
__
.
y=J
1
(X)
_._
y=J
2
(X)
_0.51....-----'------'--------1
o 5
10
15
x
Figure
8.10.
The Bessel function J
o
, J
1
,
andh.
369
We therefore obtain
the
following doubly indexed sequence of eigenvalues for
-~p
(on
the
disk
and
under Dirichlet conditions), with one or two independent eigen-
functions for each eigenvalue:
2
_
SOm
(1) (
B)
_ (Snmr) _
AmO
-
A2'
'PmO
r,
- J
o
----;r-
, m
-1,2,3,
...
,
2
\ _
Snm
(1) (
B)
_ T (Snmr)
(B)
_
Amn
-
A2
'
'Pmn
r,
- I
n
----;r-
cos n ,
m,
n -
1,2,3,
...
,
(8.44)
'P~~(r,O)
= I
n
Cn;r)
sin
(nO),
m,n
=
1,2,3,
....
Since
-~p
is symmetric under Dirichlet conditions,
we
know
that
eigenfunctions
corresponding
to
distinct eigenvalues are orthogonal.
It
turns
out
that
'Pgh
and
'P~~
are orthogonal
to
each other as well, as a direct calculation shows:
('PgL'P~~)
=
!~IoA
I
n
Cn;r)
cos (nO)J
n
Cn;r)
sin (nB)r
dr
dO
=
(1:
cos
(nO)
sin
(nO)
dO)
(loA
I
n
(Sn;rf
rdr)
=0·
(loA
Jncn;rfrdr)
=
O.

370
Chapter
8.
Problems
in
multiple
spatial dimensions
For
convenience,
we
will write
We
now
have
a
sequence
of
eigenfunctions
of
-
A
p
on
fJ
(the disk
of
radius
A
centered
at the
origin),
and
these eigenfunctions
are
orthogonal
on £7.
Just
as in
the
case
in
which
f)
was a
rectangle,
it is
possible
to
represent
any
function
in
C(0)
in
terms
of
these
eierenfunctions:
The
coefficients
are
determined
by the
usual formulas:
Using
the
properties
of the
Bessel functions developed above,
we can
simplify
(
(!) (!)
\
A ( (2)
(
2
)
^\
(VmniVmn)
and
((pmrnVmn):
and, similarly,
We
can now
represent
a
function
/(r,
0) as in
(8.46), where
370
Chapter
8.
Problems in multiple spatial dimensions
For convenience,
we
will write
Snm
amn=T'
n=0,1,2,
...
,
m=1,2,3,
....
(8.45)
We
now have a sequence of eigenfunctions of -
~p
on n (the disk of radius A
centered
at
the
origin), and these eigenfunctions are orthogonal on
n.
Just
as in
the
case in which n was a rectangle,
it
is
possible to represent any function in
Cen)
in terms of these eigenfunctions:
<Xl <Xl <Xl
m=l
m=l
n=l
The coefficients are determined by the usual formulas:
(I,
~~~)
(
(1) (1) ) ,
n =
0,1,2,
...
, m =
1,2,3,
...
,
~mn,~mn
C
mn
=
(J,~~~)
d
mn
=
-;(,.....:...(2-)--(2~)7")'
m, n =
1,2,3,
....
~mn,~mn
(8.46)
Using
the
properties of the Bessel functions developed above,
we
can simplify
(
~~~,
~~~)
and
(~~h,
~~~
) :
(~~b,
~~b)
=
i:
loA
(J
o
(a
m
or))2
r
dr
dB
=
27f
(
~2
(J1(a
m
o
A))2)
=
7fA2
(J
1
(a
m
oA))2 ,
(~~~,~~~)
=
1:loAcos2(nB)(Jn(amnr))2rdrdB
=
(1:
cos
2
(nB)
dB)
(loA
(I
n
(a
mn
r))2 r
dr)
7fA2
2
=
-2-
(In+1(a
mn
A)) ,
and, similarly,
(
(2) (2) ) _
7fA2
2
~mn'~mn
- 2 (In+1(a
mn
A)) .
We
can now represent a function
l(r,B)
as in (8.46), where
(
(1) )
I,~mn
Cmo
=
2'
m =
1,2,3,
...
,
7fA2
(J
1
(a
m
oA))

8.3.
Fourier
series
on a
disk
371
Given
that
software
routines
implementing
the
Bessel functions
are
almost
as
readily
available
as
routines
for the
trigonometric functions,
it
would
appear
that
these
formulas
are as
usable
as the
analogous
formulas
on the
rectangle.
However,
we
must
keep
in
mind
that
we do not
have formulas
for the
values
of
a
mn
.
Therefore,
to
actually
use
Bessel functions,
we
must
do a
certain
amount
of
numerical work
to
obtain
the
needed values
of
a
mn
and the
eigenvalues
\
mn
=
c?
mn
.
Example
8.7. Consider
the
function
f €
C(£l)
defined
by
where
fi
is the
unit
disk
(A =
I).
The
corresponding
function
expressed
in
polar
coordinates
is
We
wish
to
compute
an
approximation
to g
using
the
eigenfunctions
of
—
A
p
.
This
is
a
particularly simple example, since,
for any n >
0,
Similarly,
for
every
n > 0. It
follows that
g can be
represented
as
follows:
This
is not
surprising; since
g is
independent
of 9, it is
reasonable that
only
the
eigenfunctions
independent
of
9 are
needed
to
represent
g.
Since
we
must
compute numerical
estimates
of
the
eigenvalues
\
mn
,
we
will
content ourselves with using
3
eigenfunctions, those corresponding
to the
eigenvalues
8.3. Fourier
series
on
a disk
371
2
(f,
<p~h)
C
mn
= 2
2'
n =
1,2,3,
...
, m =
1,2,3,
...
,
1fA
(In+1(a
mn
A))
(8.47)
2
(1,
<p~h)
d
mn
=
2'
n =
1,2,3,
...
, m =
1,2,3,
....
1fA2
(I
n
+
1
(a
mn
A))
Given
that
software routines implementing
the
Bessel functions
are
almost as readily
available as routines for
the
trigonometric functions,
it
would
appear
that
these
formulas
are
as usable
as
the
analogous formulas
on
the
rectangle. However, we
must
keep
in
mind
that
we
do
not
have formulas for
the
values of a
mn
. Therefore,
to
actually use Bessel functions, we
must
do
a
certain
amount
of numerical work
to
obtain
the
needed values of a
mn
and
the
eigenvalues
),mn
=
a~n"
Example
8.7.
Consider the function f E
C(IT)
defined
by
f(x)
= 1 -
xi
-
x~,
where
n is the unit disk (A = 1).
The
corresponding function expressed in polar
coordinates
is
g(r,O) =
1-
r2.
We
wish
to
compute
an
approximation
to
g using the eigenfunctions of
-~p.
This
is a particularly simple example, since, for any n
> 0,
(g,
<p~h)
=
i:
11
g(r,
O)<p~~
(r,
O)r
dr
dO
= r r
1
(1
_
r2)
In(amnr) cos
(nO)r
dr
dO
1-7r
10
=
(i:
cos
(nO)
dO)
(1
1
(l-r2)
In(amnr)rdr)
=0·
(1
1
(1-r
2
)
In(amnr)rdr)
= 0.
Similarly,
(g,
<p~h)
= °
for every n >
O.
It follows that g
can
be
represented
as
follows:
00
g(r,O) = L cmOJo(amor).
m=1
This
is
not surprising; since g is independent of
0,
it
is
reasonable that only the
eigenfunctions independent
of
0
are
needed
to represent
g.
Since
we
must compute numerical estimates of the eigenvalues
),mn,
we
will
content ourselves with using
3 eigenfunctions, those corresponding
to
the eigenvalues
),10, ),20, ),30.
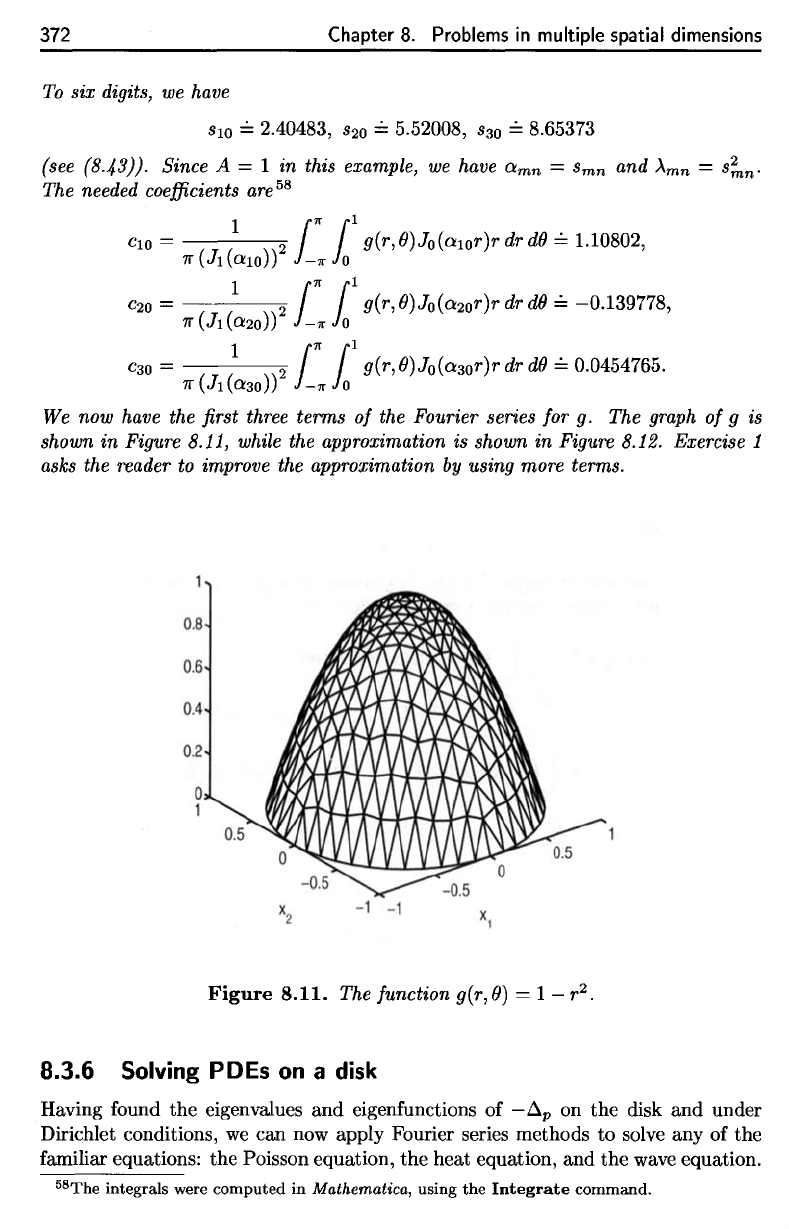
372
Chapter
8.
Problems
in
multiple
spatial dimensions
Figure
8.11.
The
function
g(r
:
9}
= 1 -
r
2
.
8.3.6
Solving
PDEs
on a
disk
Having found
the
eigenvalues
and
eigenfunctions
of
—
A
p
on the
disk
and
under
Dirichlet conditions,
we can now
apply
Fourier series methods
to
solve
any of the
familiar
equations:
the
Poisson
equation,
the
heat
equation,
and the
wave equation.
58
The
integrals were computed
in
Mathematica,
using
the
Integrate
command.
To
six
digits,
we
have
(see
(8.43)).
Since
A = 1 in
this example,
we
have
a
mn
=
s
mn
and
\
mn
=
^
mn
-
The
needed
coefficients
are
58
We
now
have
the first
three terms
of the
Fourier series
for g. The
graph
of g is
shown
in
Figure 8.11, while
the
approximation
is
shown
in
Figure 8.12. Exercise
1
asks
the
reader
to
improve
the
approximation
by
using more
terms.
372
Chapter
8.
Problems
in
multiple spatial dimensions
To
six digits,
we
have
SlO
==
2.40483,
S20
==
5.52008,
S30
==
8.65373
{see
{8.43}}.
Since A = 1 in this example,
we
have
Q
mn
=
Smn
and
Amn
=
s~n'
The
needed
coefficients
are
58
ClO = 1
2111"
(l
g(r,())J
o
(QlO
r
)rdrd()
==
1.10802,
rr(Jl(QlO))
-1I"i
o
C20
= 1
2111"
(l
g(r, ())J
O
(Q20r)r
dr d()
==
-0.139778,
rr(Jl(Q20))
-1I"i
o
C30
= 1
2111"
(l
g(r,())J
o
(Q30
r
)rdrdfJ
==
0.0454765.
rr(Jl(Q30))
-1I"i
o
We
now
have the first
three
terms
of
the Fourier series for
g.
The
graph
of 9
is
shown in Figure 8.11,
while
the approximation is shown in
Figure
8.12. Exercise 1
asks
the reader
to
improve the approximation
by
using more terms.
0.8
0.6
0.4
0.2
o
1
-1 -1
Figure
8.11.
The
function g(r,
())
= 1 -
r2.
8.3.6
Solving
PDEs
on
a
disk
Having found
the
eigenvalues and eigenfunctions of
-Ll
p
on the disk and under
Dirichlet conditions,
we
can now apply Fourier series methods
to
solve any of the
familiar equations: the Poisson equation, the heat equation, and the wave equation.
58The integrals were
computed
in Mathematica, using
the
Integrate
command.
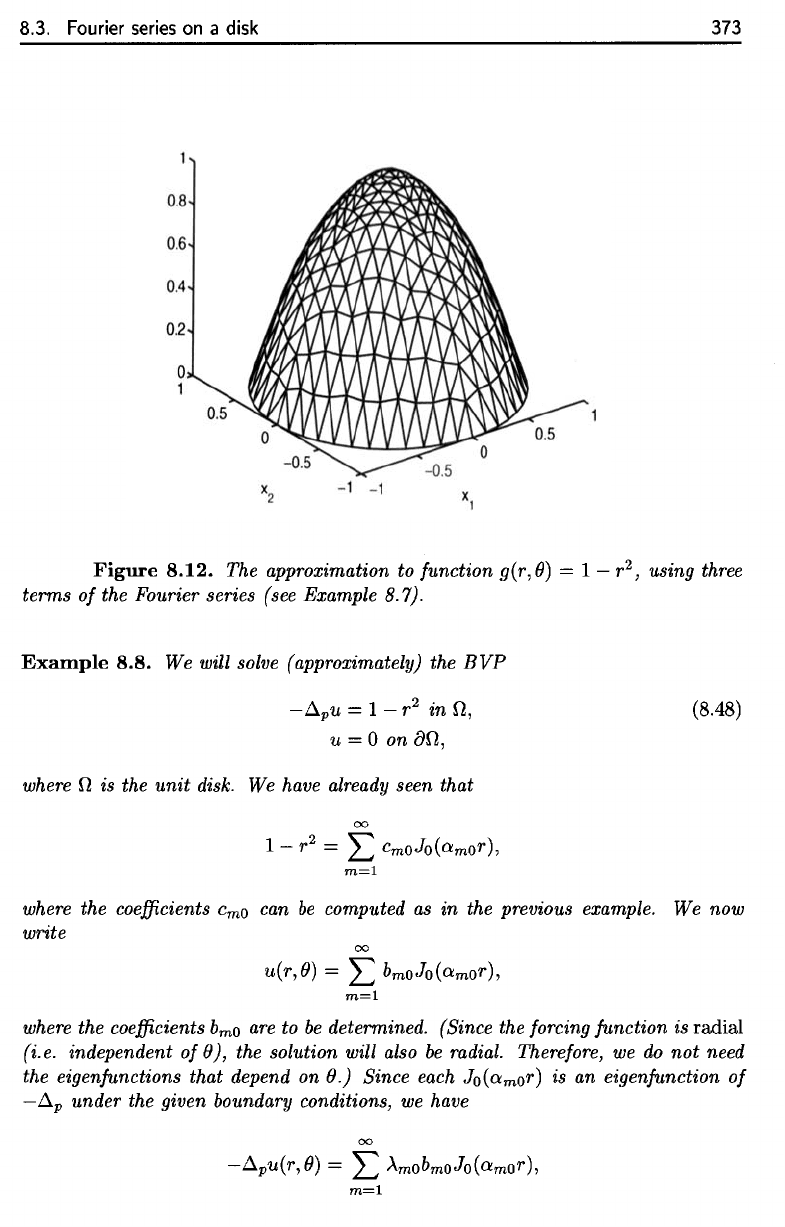
8.3. Fourier series
on a
disk
373
Figure
8.12.
The
approximation
to
function
g(r,0]
=
I
—
r
2
,
using three
terms
of the
Fourier
series
(see Example
8.7).
where
the
coefficients
c
m
o
can be
computed
as in the
previous
example.
We now
write
where
the
coefficients
b
m
o
are to be
determined.
(Since
the
forcing
function
is
radial
(i.e. independent
of 0), the
solution
will also
be
radial. Therefore,
we do not
need
the
eigenfunctions
that
depend
on 9.)
Since
each
Jo(a
m
Qr)
is an
eigenfunction
of
—A
p
under
the
given
boundary
conditions,
we
have
Example
8.8.
We
will solve (approximately)
the BVP
where
0,
is the
unit
disk.
We
have
already
seen
that
8.3. Fourier
series
on
a disk
373
- 1 -1
Figure
8.12.
The approximation to function g(r,
0)
= 1 - r2, using three
terms
of
the Fourier series (see Example 8.7).
Example
8.8.
We will solve (approximately) the
BVP
-.:lpu
= 1 -
r2
in
n,
u = 0 on
an,
where n is the
unit
disk. We have already seen that
00
1 -
r2
= L cmOJo(amor),
m=l
(8.48)
where the coefficients
CmO
can
be
computed
as
in the previous example. We now
write
00
u(r,B) = L bmoJo(amor),
m=l
where the coefficients b
mo
are to
be
determined. (Since the forcing function is radial
(i.e. independent
of
B), the solution will also
be
radial. Therefore,
we
do
not
need
the eigenfunctions that depend on B.) Since each Jo(amor) is an eigenfunction
of
-.:lp
under the given boundary conditions,
we
have
00
-.:lpu(r,O) = L AmObmOJo(amor),
m=l

374
Chapter
8.
Problems
in
multiple
spatial dimensions
where
the
eigenvalue
A
m
o
is
given
by
A
m
o
=
#mo
•
Therefore,
the PDE
implies that
and
so the
solution
is
We
computed
C\Q,
c^o,
c^o,
«iO;
&2Q,
o,nd
0,3$
in the
previous example,
so we see
that
Example
8.9.
We
will
now
solve
the
wave equation
on a
disk
and
compare
the
fundamental frequency
of a
circular drum
to
that
of a
square drum.
We
consider
the
IBVP
where
f)
is the
disk
of
radius
A,
centered
at the
origin.
We
write
the
solution
as
Then,
by the
usual argument,
The
wave equation then implies
the
following
ODEs:
374 Chapter 8. Problems
in
multiple spatial dimensions
where
the eigenvalue
AmO
is
given
by
AmO
=
a~o.
Therefore, the PDE implies that
AmObmO
=
Cmo,
m =
1,2,3,
...
,
and
so
the solution
is
00
u(r,
B)
= L
c~o
Jo(amor).
m=1
a
mO
We
computed
ClO,
C20,
C30,
alO,
a20,
and
a30
in the previous example,
so
we
see
that
u(r,B)
= 0.191594J
o
(alOr)
- 0.00458719J
o
(a2or)
+ 0.000607268Jo(a30r) + ....
Example
8.9.
We
will now
solve
the
wave
equation
on
a
disk
and
compare
the
fundamental frequency
of
a circular drum
to
that of a
square
drum.
We
consider
the
IBVP
(Pu
at
2
-
c
2
Ll
p
u = 0, (r,B) E fl, t > 0,
u(r,B,O) = ¢(r,B), (r,B) E fl,
au
at
(r,
B,
0)
=
'Y(r,
B),
(r,
B)
E fl,
u(A,B,
t)
= 0,
-7r
~
B <
7r,
t>
0,
(8.49)
(8.50)
(8.51)
where
fl is the disk of radius A, centered at the origin.
We
write the solution
as
00
u(r,
B,
t) = L amo(t)Jo(amor)
m=1
00
00
+ L L (amn(t) cos
(nB)
+ bmn(t) sin
(nB))
In(amnr).
m=1
n=1
Then,
by
the usual argument,
a
2
u 2
~
(dla
m
o
2 )
at
2
(r,
B,
t) - C Llpu(r,
B,
t)
=;;;:1
~(t)
+ C
AmOamO(t)
Jo(amor)
+
~1
~
(
(,pd~;n
(t)
+ C
2
Amnamn(t)) cos
(nB)
+
(,p!r;n
(t) + C
2
Amnbmn(t)) sin (nB)) In(amnr).
The
wave
equation then implies the following
ODEs:
,pamn 2
~
+C
Amnamn
= 0, m = 1,2,3,
...
,n
=
0,1,2,
...
,
d
2
b
mn
2
~
+ C
Amnb
mn
=
0,
m,n
=
1,2,3,
....

It
would
be
reasonable
to
compare
a
circular drum
of
radius
A
(diameter
1A)
with
a
square drum
of
side length
1A.
(Another possibility
is to
compare
the
circular
drum with
a
square drum
of the
same area. This
is
Exercise
9.) The
fundamental
frequency
of
such
a
square drum
is
The
square drum sounds
a
lower frequency than
the
circular drum.
Exercises
1.
Let
g(r,9)
= 1
—
r
2
,
as in
Example 8.7. Compute
the
next
three
terms
in the
series
for
g.
2.
Let
f(r,9]
=
I
—
r.
Compute
the first
nine
terms
in the
generalized Fourier
series
for /
(that
is,
those
corresponding
to the
eigenvalues
Take
fJ
to be the
unit disk.
8.3.
Fourier
series
on a
disk
375
From
the
initial conditions
for the
PDE,
we
obtain
where
c
mn
,
d
mn
are the
(generalized)
Fourier
coefficients
for
<f>,
and
e
mn
,
f
mn
are
the
(generalized)
Fourier
coefficients
for 7. By
applying
the
results
of
Section
4-7
and
using
the
fact that
\
mn
—
o^
nn
,
we
obtain
the
following formulas
for the
coefficients
of the
solution:
The
smallest period
of any of
these
coefficients
is
that
of
0,1$:
The
corresponding frequency, which
is the
fundamental frequency
of
this circular
drum,
is
8.3. Fourier
series
on
a disk
375
From the initial conditions for the PDE,
we
obtain
amn(O)
= c
mn
'
damn
(0) = d 2 3 0 1 2
dt mn, m = 1, , ,
...
, n = , , ,
...
,
bmn(O)
= e
mn
,
db
mn
( )
--;]i'" 0 = fmn,
m,
n =
1,2,3,
...
,
where C
mn
' d
mn
are the (generalized) Fourier coefficients for
l/J,
and e
mn
, fmn
are the (generalized) Fourier coefficients for
'Y.
By
applying the results
of
Section
4.7
and using the fact that
Amn
=
O:~n'
we
obtain the following formulas for the
coefficients
of
the solution:
amn(t)
= C
mn
cos (co:mnt) + d
mn
sin
(Co:mnt)
, m =
1,2,3,
...
, n =
0,
1,2,
...
,
CO:
mn
bmn(t)
= e
mn
cos (co:mnt) + fmn sin
(Co:mnt)
, m, n =
1,2,3,
....
CO:
mn
The smallest period
of
any
of
these coefficients is that
of
aw:
Tw=
~
=
~=
2A1l'.
Co: 10
csodA
CSOl
The corresponding frequency, which is the fundamental frequency
of
this circular
drum, is
F = CSOl =
~
SOl
==
0
382740~
10
2A1l'
A
21l"
A .
It
would
be
reasonable to compare a circular drum
of
radius A (diameter
2A)
with
a square drum
of
side length 2A. (Another possibility is to compare the circular
drum with a square drum
of
the same area. This is Exercise 9.) The fundamental
frequency
of
such a square drum is
The square drum sounds a lower frequency than the circular drum.
Exercises
1.
Let g(r,
B)
= 1 - r2, as in Example 8.7. Compute the next three terms in the
series for
g.
2.
Let f(r,B) =
1-
r. Compute
the
first nine terms in
the
generalized Fourier
series for
f
(that
is, those corresponding to the eigenvalues
Take
n
to
be
the
unit disk.

376
Chapter
8.
Problems
in
multiple spatial dimensions
3.
Solve
the BVP
where
£7
is the
unit disk. Graph
the
solution. (Hint: Change
to
polar coordi-
nates
and use the
results
of the
previous exercise.)
4.
Let
/(r,
9} = r.
Compute
the first
nine terms
in the
generalized Fourier series
for
/
(that
is,
those corresponding
to the
eigenvalues
Take
f2
to be the
unit disk.
5.
Solve
the BVP
where
£7 is the
unit disk. Graph
the
solution. (Hint: Change
to
polar coordi-
nates
and use the
results
of the
previous exercise.)
6.
Let
/(x)
= (1
—
#1
—
Xz)(xi
+
xz).
Convert
to
polar coordinates
and
compute
the first 16
terms
in the
(generalized) Fourier series (that
is,
those correspond-
ing
to
A
mn
,
m
=
1,2,3,4,
n
—
0,1,2,3).
Graph
the
approximation
and its
error.
7.
Consider
a
disk made
of
copper
(p =
8.97g/cm
3
,
c =
0.379J/(gK),
K
=
4.04
W/(cmK)),
of
radius
10cm.
Suppose
that
the
temperature
in the
disk
is
initially
4>(r,6)
=
rcos
(0)(10
—
r)/5.
What
is the
temperature distribution
after
30
seconds (assuming
that
the top and
bottom
of the
disk
are
perfectly
insulated,
and the
edge
of the
disk
is
held
at 0
degrees
Celsius)?
8.
Consider
an
iron disk
(p
=
7.88
g/cm
3
,
c =
0.437
J/(gK),
«
=
0.836W/(cmK))
of
radius
15
cm.
Suppose
that
heat energy
is
added
to the
disk
at the
constant
rate
of
where
the
disk occupies
the set
Assume
that
the top and
bottom
of the
disk
are
perfectly insulated
and
that
the
edge
of the
disk
is
held
at 0
degrees Celsius.
(a)
What
is the
steady-state
temperature
of the
disk?
(b)
Assuming
the
disk
is
initially
0
degrees Celsius throughout,
how
long
does
it
take
for the
disk
to
reach steady
state
(to
within
1%)?
376
Chapter
8.
Problems
in
multiple spatial dimensions
3.
Solve the BVP
-~u
= 1 - V x
2
+
y2
in
0,
u = 0 on
a~,
where 0
is
the unit disk. Graph
the
solution. (Hint: Change to polar coordi-
nates and use the results of
the
previous exercise.)
4.
Let f(r,O) = r. Compute
the
first nine terms in the generalized Fourier series
for
f
(that
is, those corresponding
to
the
eigenvalues
Take
0
to
be the unit disk.
5.
Solve
the
BVP
-~u
=
VX2
+y2
in
0,
u = 0 on
a~,
where 0
is
the unit disk. Graph the solution. (Hint: Change
to
polar coordi-
nates and use the results of
the
previous exercise.)
6.
Let
f(x)
=
(1-
xi
-
X~)(XI
+
X2).
Convert to polar coordinates and compute
the
first
16
terms in the (generalized) Fourier series
(that
is, those correspond-
ing
to
A
mn
, m =
1,2,3,4,
n =
0,1,2,3).
Graph
the
approximation and its
error.
7.
Consider a disk made of copper
(p
= 8.97 g/cm
3
,
c = 0.379 J/(gK), K, =
4.04
WI
(cm K)), of radius
10
cm. Suppose
that
the temperature in
the
disk
is initially
¢(r,
0)
= r
cos
(0)(10 - r)/5.
What
is
the
temperature distribution
after
30
seconds (assuming
that
the top and bottom of the disk are perfectly
insulated, and the edge of the disk
is
held
at
0 degrees Celsius)?
8.
Consider
an
iron disk
(p
= 7.88
gl
cm
3
,
c = 0.437 J I
(g
K), K, = 0.836
WI
(em K))
of radius
15
cm. Suppose
that
heat energy
is
added to the disk
at
the
constant
rate
of
f(r,O) =
I~Or(sin
(0)
+
eos
(0)) W
lem
3
,
where the disk occupies the set
0=
{(r,O) :
r<15}.
Assume
that
the
top
and
bottom
of the disk are perfectly insulated and
that
the edge of the disk
is
held
at
0 degrees Celsius.
(a)
What
is
the steady-state temperature of
the
disk?
(b) Assuming
the
disk
is
initially 0 degrees Celsius throughout, how long
does it take for
the
disk
to
reach steady state (to within 1%)?

8.4.
Finite
elements
in two
dimensions
377
9.
Which
has a
lower fundamental
frequency,
a
square drum
or a
circular drum
of
equal area?
10.
Show
that
(8.41) holds
by
deriving
the
power series
for the
right-hand side
and
showing
that
it
simplifies
to the
power series
for the
left-hand side.
8.4
Finite
elements
in two
dimensions
We
now
turn
our
attention
to finite
element methods
for
multidimensional problems.
For
the
sake
of
simplicity,
we
will
restrict
our
attention
to
problems
in two
spatial
dimensions and,
as in one
dimension,
to
piecewise linear
finite
elements.
The
general
outline
of the finite
element method does
not
change
when
we
move
to
two-dimensional space.
The finite
element method
is
obtained
via the
following
steps:
1.
Derive
the
weak
form
of the
given BVP.
2.
Apply
the
Galerkin method
to the
weak
form.
3.
Choose
a
space
of
piecewise polynomials
for the
approximating subspace
in
the
Galerkin method.
The first
step
is
very similar
to the
derivation
in one
dimension;
as one
might
expect,
the
main
difference
is
that
integration
by
parts
is
replaced
by
Green's
first
identity.
The
Galerkin method
is
unchanged when applied
to a
two-dimensional
problem.
The
most significant
difference
in
moving
to
two-dimensional problems
is
in
defining
the finite
element spaces.
We
must create
a
mesh
on the
computational
domain
and
define
piecewise polynomials
on the
mesh.
We
will
restrict ourselves
to
triangulations
and
piecewise linear
functions.
8.4.1
The
weak
form
of a BVP in
multiple
dimensions
We
begin with
the
following
Dirichlet problem:
Here
f)
is a
domain
in R
2
or R
3
;
there
is no
difference
in the
following
derivation.
We
define
the
space
V of
test
functions
by
We
then multiply
the
original
PDE by an
arbitrary
v € V and
apply Green's
identity:
8.4.
Finite elements
in
two dimensions
377
9.
Which has a lower fundamental frequency, a square
drum
or a circular
drum
of equal area?
10. Show
that
(8.41) holds by deriving
the
power series for
the
right-hand side
and
showing
that
it
simplifies
to
the
power series for
the
left-hand side.
8.4 Finite elements
in
two
dimensions
We
now
turn
our attention
to
finite element methods for multidimensional problems.
For
the
sake of simplicity,
we
will restrict our attention
to
problems in two spatial
dimensions and, as in one dimension,
to
piecewise linear finite elements.
The
general outline of
the
finite element method does
not
change when
we
move
to
two-dimensional space.
The
finite element method is obtained via
the
following steps:
1.
Derive
the
weak form of
the
given BVP.
2.
Apply
the
Galerkin method
to
the
weak form.
3.
Choose a space of piecewise polynomials for
the
approximating subspace in
the
Galerkin method.
The
first step
is
very similar
to
the
derivation in one dimension; as one might
expect,
the
main difference
is
that
integration by
parts
is replaced by Green's first
identity.
The
Galerkin method is unchanged when applied
to
a two-dimensional
problem.
The
most significant difference in moving
to
two-dimensional problems is
in defining
the
finite element spaces.
We
must create a mesh on
the
computational
domain
and
define piecewise polynomials on
the
mesh.
We
will restrict ourselves
to
triangulations
and
piecewise linear functions.
8.4.1 The
weak
form
of a
BVP
in
multiple
dimensions
We
begin with
the
following Dirichlet problem:
-
\7
. (k(x)\7u) =
f(x),
x E
0,
u(x) = 0, x E
ao.
(8.52)
Here 0
is
a domain in R2 or R3; there
is
no difference in
the
following derivation.
We
define
the
space V
of
test
functions by
V =
eben)
= {v E e
2
(n) : v(x) =
0,
x E ao}.
We
then
multiply
the
original
PDE
by
an
arbitrary
v E V
and
apply Green's
identity:
-\7.
(k(x)\7u)(x) =
f(x),
x E 0
::::}
-\7.
(k(x)\7u(x))v(x) =
f(x)v(x),
x E
0,
v E V
::::}
-In
\7
. (k(x)\7u)v =
In
fv
for all v E V
