Gockenbach M.S. Partial Differential Equations. Analytical and Numerical Methods

338

Chapter

8.

Problems

in

multiple

spatial

dimensions

2.

Let

0

C R

2

be the

rectangular domain

and

let F : R

2

—»•

R

2

be a

smooth vector

field.

Prove

that

Hint: Rewrite

the

area

integral

on the

left

as an

iterated integral

and

apply

the

fundamental theorem

of

calculus. Compare

the

result

to the

boundary

integral

on the

right.

3. Let

£7

C

R

2

be the

unit square:

Define

F : ft

->

R

2

by

Verify

that

the

divergence theorem holds

for

this

domain

fl

and

this

vector

field F.

4.

Let

il

C

R

2

be the

unit disk:

Define

F : ft

-»

R

2

by

Verify

that

the

divergence theorem holds

for

this domain

Q

and

this

vector

field F.

5.

Prove (8.8)

as

follows:

Write

and

apply

the

ordinary (scalar) product rule

to

each term

on the

right.

6.

Define

and

Show

that

LN

is

symmetric:

338

Chapter

8.

Problems

in

multiple spatial dimensions

2.

Let

nCR

2

be the rectangular domain

n =

{x

E R2 : a <

Xl

<

b,

c <

X2

<

d}

,

and let F : R

2

-+

R

2

be a smooth vector field. Prove

that

r

\7

. F = r

F·

n.

ln

len

Hint: Rewrite the area integral on the left as an iterated integral

and

apply

the

fundamental theorem of calculus. Compare

the

result to the boundary

integral on

the

right.

3.

Let n c R2 be the unit square:

n =

{x

E R2 : 0 <

Xl

<

1,

0 <

X2

<

I}

.

Define F : n

-+

R2 by

F(x) = [

X+2

] •

Xl

X2

Verify

that

the

divergence theorem holds for this domain n and this vector

field

F.

4.

Let n c R2 be the unit disk:

n = {x E R2 : xi +

x~

<

I}

.

Define F : n

-+

R2 by

F(x) = [

X2

] .

Xl

+

X2

Verify

that

the divergence theorem holds for this domain n and this vector

field

F.

5.

Prove (8.8) as follows: Write

3 0 [ 0 ]

\7.

(v\7u) = L -

v~

.

OXi OXi

.=1

and apply the ordinary (scalar) product rule

to

each term on the right.

6.

Define

and

LN

:

C~(n)

-+

C(n),

LNU

=

-~U.

Show

that

LN

is

symmetric:

8.2. Fourier series

on a

rectangular domain

339

7.

Suppose

that

the

boundary

of £7 is

partitioned into

two

disjoint

sets:

dtl

—

FI

UF

2

.

Define

and

Show

that

L

m

is

symmetric:

8.

Verify

that

the

solution

to

(8.6)

is

also

the

solution

to

(8.5).

8.2

Fourier

series

on a

rectangular

domain

We

now

develop Fourier series methods

for the

fundamental equations (Poisson's

equation,

the

heat equation,

and the

wave equation)

on the

two-dimensional rect-

angular domain

We

will

begin

by

discussing Dirichlet conditions,

so the

operator

is

Lp,

as

defined

at the end of the

last

section.

8.2.1

Dirichlet

boundary

conditions

As

we

should expect

from

the

development

in

Chapters

5, 6, and 7, the

crux

of

the

matter

is to

determine

the

eigenvalues

and

eigenfunctions

of

Lp.

We

have

already seen

that

LD

is

symmetric,

so we

know

that

eigenfunctions corresponding

to

distinct eigenvalues must

be

orthogonal.'

Moreover,

it is

easy

to

show directly

that

LD

has

only positive eigenvalues.

For

suppose

A is an

eigenvalue

of

LD

and

u

is

a

corresponding

eigenfunction,

normalized

to

have norm

one

(the norm

is

derived

from

the

inner product:

||w||

=

^(u,u)}.

Then

with

the

last

step

following

from

Green's

first

identity

and the

fact

that

u

vanishes

on the

boundary

of

f).

Since

this certainly shows

that

A

>

0.

Moreover,

8.2. Fourier

series

on

a rectangular domain

339

7.

Suppose

that

the boundary of n

is

partitioned into two disjoint sets:

an

=

r

1

u r

2

.

Define

and

Lm :

C~01)

-t

C(O),

Lmu

=

-~u.

Show

that

Lm

is

symmetric:

2 -

(Lmu,v)

=

(u,Lmv)

for all

U,V

E

Cm(n).

8.

Verify

that

the

solution to (8.6)

is

also the solution

to

(8.5).

8.2 Fourier

series

on

a rectangular domain

We

now develop Fourier series methods for the fundamental equations (Poisson's

equation, the heat equation, and the wave equation) on

the

two-dimensional rect-

angular domain

(8.10)

We

will begin by discussing Dirichlet conditions, so the operator

is

L

D

,

as defined

at

the end of the last section.

8.2.1 Dirichlet boundary conditions

As

we

should expect from the development in Chapters

5,

6,

and

7,

the crux of

the

matter

is

to determine the eigenvalues and eigenfunctions of L

D

.

We

have

already seen

that

LD

is

symmetric,

so

we

know

that

eigenfunctions corresponding

to distinct eigenvalues must be orthogonal: Moreover,

it

is

easy

to

show directly

that

LD has only positive eigenvalues. For suppose A

is

an eigenvalue of LD and u

is

a corresponding eigenfunction, normalized

to

have norm one (the norm

is

derived

from

the

inner product:

Ilull

=

v(u,u)).

Then

A =

A(U,U)

=

(AU,U)

=

(LDu,u)

=

-lLlUU

= l

V'u·

V'u,

with

the

last step following from Green's first identity and the fact

that

u vanishes

on the boundary of

n.

Since

V'u·

V'u

=

IIV'ul1

2

:2:

0,

this certainly shows

that

A

:2:

O.

Moreover,

illV'u

W

= 0

340

Chapter

8.

Problems

in

multiple spatial dimensions

only

if

Vw

is

identically equal

to the

zero vector.

But

this holds only

if

u

is a

constant

function,

and,

due to the

boundary conditions,

the

only

constant

function

in

Cpfil)

is the

zero

function.

By

assumption

||w||

= 1, so u is not the

zero

function.

Thus

we see

that,

in

fact,

A > 0

must hold. This proof

did not use the

particular

form

of

fJ,

and the

result

is

therefore true

for

nonrectangular

domains.

Thus

we

wish

to find all

positive values

of A

such

that

the BVP

has a

nonzero solution.

We are now

faced with

a PDE for

which

we

have

no

general

solution techniques.

We

fall

back

on a

time-honored approach: make

an

inspired

guess

as to the

general

form

of the

solution, substitute into

the

equation,

and try

to

determine

specific

solutions.

We

will

look

for

solutions

of the

form

that

is,

functions

of two

variables

that

can be

written

as the

product

of two

func-

tions, each with only

one

independent variable. Such

functions

are

called

separated,

and

this

technique

is

called

the

method

of

separation

of

variables.

We

therefore

sunnose

that

w,(x1

=

wi

(x-i

}u^(x^}

satisfies

We

have

so

the PDE

becomes

Dividing

through

by

u\ui

yields

If

we

rewrite this

as

we

obtain

the

conclusion

that

both

340

Chapter

8.

Problems

in

multiple spatial dimensions

only if \7u

is

identically equal

to

the

zero vector.

But

this holds only

if

U

is

a

constant function, and, due

to

the boundary conditions, the only constant function

in

C1(n)

is the zero function. By assumption

Ilull

=

1,

so u

is

not

the

zero function.

Thus

we

see

that,

in fact, A > 0 must hold. This proof did not use the particular

form

of

n,

and the result

is

therefore

true

for nonrectangular domains.

Thus

we

wish

to

find all positive values of A such

that

the

BVP

-Llu

=

AU,

x E

n,

u = 0, x E

an

(8.11)

has a nonzero solution.

We

are now faced with a

PDE

for which

we

have no general

solution techniques.

We

fall back on a time-honored approach: make

an

inspired

guess as

to

the

general form of the solution, substitute into the equation, and

try

to

determine specific solutions.

We

will look for solutions of the form

that

is, functions of two variables

that

can

be

written as the product of two func-

tions, each with only one independent variable. Such functions are called

separated,

and this technique is called

the

method of separation

of

variables.

We

therefore suppose

that

u(x)

= U1

(XdU2(X2)

satisfies

-Llu

=

AU,

x E

n.

We

have

so

the

PDE

becomes

Dividing through by

U1

U2

yields

-1

~U1

-1

~U2

-U

1

-d

2 - U

2

-d

2 =

A,

(X1,X2)

En.

Xl

X

2

If

we

rewrite this as

(8.12)

we

obtain

the

conclusion

that

both

-1

d

2

u1

-1

~U2

U

1

-d

2 and U

2

_d

2

Xl

X

2

8.2. Fourier

series

on a

rectangular domain

341

must

be

constant

functions.

For on the

left

side

of

(8.12)

is a

function depending

only

on

x\,

and on the

right

is a

function depending only

on

X2.

If we

differentiate

with

respect

to

0:1,

we see

that

the

derivative

of the first

function

must

be

zero,

and

hence

that

the

function itself must

be

constant. Similarly,

the

second function

must

be

constant.

We

have therefore shown

the

following:

If A is

positive

and

has a

solution

of the

form

w(#i,£2)

=

^(x^u^x^)-,

then

u\

and

u%

satisfy

where

9\

+

62

= A.

These

we can

rewrite

as

and so we

obtain ODEs

for

u\

and

u^.

Moreover,

we can

easily

find

boundary conditions

for the

ODEs, since

the

boundary conditions

on the PDE

also

separate.

The

boundary

of

0

consists

of four

line

segments

(see

Figure

8.3):

On

FI

, for

example,

we

have

(There

is

also

the

possibility

that

u\(x\)

=

0, but

then

u is the

zero

function,

and

we

are

only

interested

in

nontrivial

solutions.)

By

similar reasoning,

we

obtain

Our

problem

now

reduces

to finding

nonzero solutions

to the

BVPs

and

8.2. Fourier

series

on

a rectangular domain

341

must be constant functions. For on

the

left side of (8.12)

is

a function depending

only on

Xl,

and on

the

right

is

a function depending only on

X2.

If

we

differentiate

with respect

to

Xl,

we

see

that

the

derivative of

the

first function must be zero,

and hence

that

the function itself must be constant. Similarly,

the

second function

must

be

constant.

We

have therefore shown the following:

If

A

is

positive and

-~u

=

AU,

x E n

has a solution of

the

form U(Xl,

X2)

=

Ul

(Xl)U2(X2), then

Ul

and

U2

satisfy

-1

~Ul

-1

d

2

u2

-U

l

-d

2 =

(h,

-U

2

-d

2 = ()2,

Xl

X

2

where ()1 + ()2 =

A.

These

we

can rewrite as

d

2

u1

--d

2 =

()l

U

l,

Xl

and

so

we

obtain ODEs for

U1

and

U2.

Moreover,

we

can easily find boundary conditions for

the

ODEs, since

the

boundary conditions on the

PDE

also separate.

The

boundary of n consists of four

line segments (see Figure 8.3):

f1

= {(X1,X2)

X2

=

0,

0::;

Xl

::;

£t}

(bottom),

f2

= {(X1,X2)

Xl

= £1, 0::;

X2

::;

£2}

(right),

(8.13)

f3

= {(X1,X2)

X2

= £2, 0::;

Xl

::;

£1}

(top),

f4

= {(X1,X2)

Xl

= 0, 0::;

X2

::;

£2}

(left).

On

f

1,

for example,

we

have

U = 0

=}

Ul(Xt}U2(0) = 0

=}

U2(0)

=

O.

(There

is

also

the

possibility

that

U1

(xt)

==

0,

but

then U

is

the

zero function, and

we

are only interested in nontrivial solutions.) By similar reasoning,

we

obtain

and

U1(0)

=

u1(£d

= 0,

U2(0)

=

U2(£2)

=

o.

Our problem now reduces

to

finding nonzero solutions

to

the BVPs

~Ul

--d

2 =

()lUl,

0 <

Xl

<

£1,

Xl

U1(0)

= 0,

U1(£1)

=0

~U2

--d

2 = ()2

U

2,

0 <

X2

<

£2,

X

2

U2(0)

= 0,

U2(£2)

= 0,

(8.14)

(8.15)

342

Chapter

8.

Problems

in

multiple spatial

dimensions

Figure

8.3.

The

domain

fJ

and its

boundary.

where

9\

and

#2

can be any

real numbers adding

to A. But we

have already solved

these problems

(in

Section 5.2).

For

(8.14),

the

permissible values

of

B\

are

For

(8.15),

we

have

We

have succeeded

in

computing

all the

eigenvalue-eigenfunction pairs

of

LD

in

which

the

eigenfunctions

are

separated.

We

have

no

guarantee

(at

least,

not

from

our

analysis

so

far)

that

there

are not

other eigenpairs with nonseparated

eigenfunc-

tions. However,

it

turns

out

that

this question

is not

particularly important, because

and the

corresponding eigenfunctions

are

and the

corresponding eigenfunctions

are

Any

solution

to

(8.14) times

any

solution

to

(8.15)

forms

a

solution

to

(8.11),

so we

obtained

a

doublv indexed sequence

of

solutions

to

(8.11):

342 Chapter

8.

Problems

in

multiple spatial dimensions

r,

Figure

8.3.

The domain n and its boundary.

where

(h

and

(h

can be any real numbers adding

to

A.

But

we

have already solved

these problems (in Section 5.2). For (8.14),

the

permissible values of

(h

are

and

the

corresponding eigenfunctions are

(m)

) _ .

(m1l'XI)

_

'ljJ1

(Xl

- sm

-------;;;--

, m -

1,2,3,

....

For (8.15),

we

have

(n)

_ n

2

1l'2

(}2

-

e~

, n =

1,2,3,

...

,

and

the

corresponding eigenfunctions are

(m)(

) _ . (n1l'X2) _

'ljJ2

X2

-sm

T '

n-1,2,3,

....

Any solution

to

(8.14) times any solution

to

(8.15) forms a solution

to

(8.11), so

we

obtained a doubly indexed sequence of solutions

to

(8.11):

m

2

1l'2

n

2

1l'2

Amn=-r+T'

I 2

(8.16)

'ljJmn(XI,X2)

= sin

(m;IXI)

sin

(n;:2),

m,n

=

1,2,3,

....

We

have succeeded in computing all

the

eigenvalue-eigenfunction pairs of

LD

in which the eigenfunctions are separated.

We

have no guarantee (at least, not from

our analysis

so

far)

that

there are not other eigenpairs with nonseparated eigenfunc-

tions. However, it turns out

that

this question is not particularly important, because

8.2. Fourier

series

on a

rectangular

domain

343

we

can

show

that

the

eigenpairs (8.16)

are

sufficient

for our

purposes. Indeed,

it is

not

difficult

to

argue

that

every

function

u

£

C(ft)

should

be

representable

as

where

the

convergence

is in the

mean-square sense.

We

will

call such

a

series

a

Fourier (double) sine series.

We

consider

any u =

u(xi,x<2)

(not necessarily satisfy-

ing

the

Dirichlet boundary

conditions).

Regarding

x%

€

(0,^)

as a

parameter,

we

can

write

where

But now

b

m

is a

function

of

#2

€

(0,^2)

that

can be

expanded

in a

Fourier sine

corioc

QC

iiroll-

where

Putting

these results together,

we

obtain

with

Equation (8.17)

is

valid

in the

mean-square sense.

It is

straightforward

to

show

that

formulas (8.17), (8.18)

are

exactly what

the

projection theorem produces;

that

is,

is

the

best approximation

to u, in the

L

2

norm,

from

the

subspace spanned

by

(see

Exercise

6).

8.2. Fourier

series

on a rectangular domain

343

we

can show

that

the eigenpairs (8.16) are sufficient for our purposes. Indeed,

it

is

not difficult

to

argue

that

every function U E

CeO)

should be representable as

where the convergence

is

in the mean-square sense.

We

will call such a series a

Fourier (double) sine series.

We

consider any U = U(Xl,X2) (not necessarily satisfy-

ing the Dirichlet boundary conditions). Regarding

X2

E (0'£2) as a parameter,

we

can write

where

b

m

(X2)

=

£~

1£1

U(Xl,X2) sin

(m~Xl)

dXl.

But

now b

m

is

a function of

X2

E

(0,

£2)

that

can be expanded in a Fourier sine

series as

well:

where

a

mn

=

~

1£2

b

m

(X2)

sin

(n;:2

)

dX2.

Putting

these results together,

we

obtain

(8.17)

with

(8.18)

Equation (8.17)

is

valid in the mean-square sense.

It

is

straightforward to show

that

formulas (8.17), (8.18) are exactly what the

projection theorem produces;

that

is,

~ ~

.

(m7rXl)

. (n7rX2)

~l

~

a

mn

sm --y;- sm T

is

the best approximation to u, in the

L2

norm, from

the

subspace spanned by

{~mn:

m=1,2,

...

,M,

n=1,2,

...

,N}

(see Exercise 6).

344

Chapter

8.

Problems

in

multiple

spatial

dimensions

In

Figure

8.4,

we

graph

the

resulting partial series approximation

to

u,

using

M

=

20

and

N = 20

(for

a

total

of 400

terms).

Gibbs's phenomenon

is

clearly

visible,

as

would

be

expected

since

u

only

satisfies

the

Dirichlet

boundary

conditions

on

part

of

the

boundary.

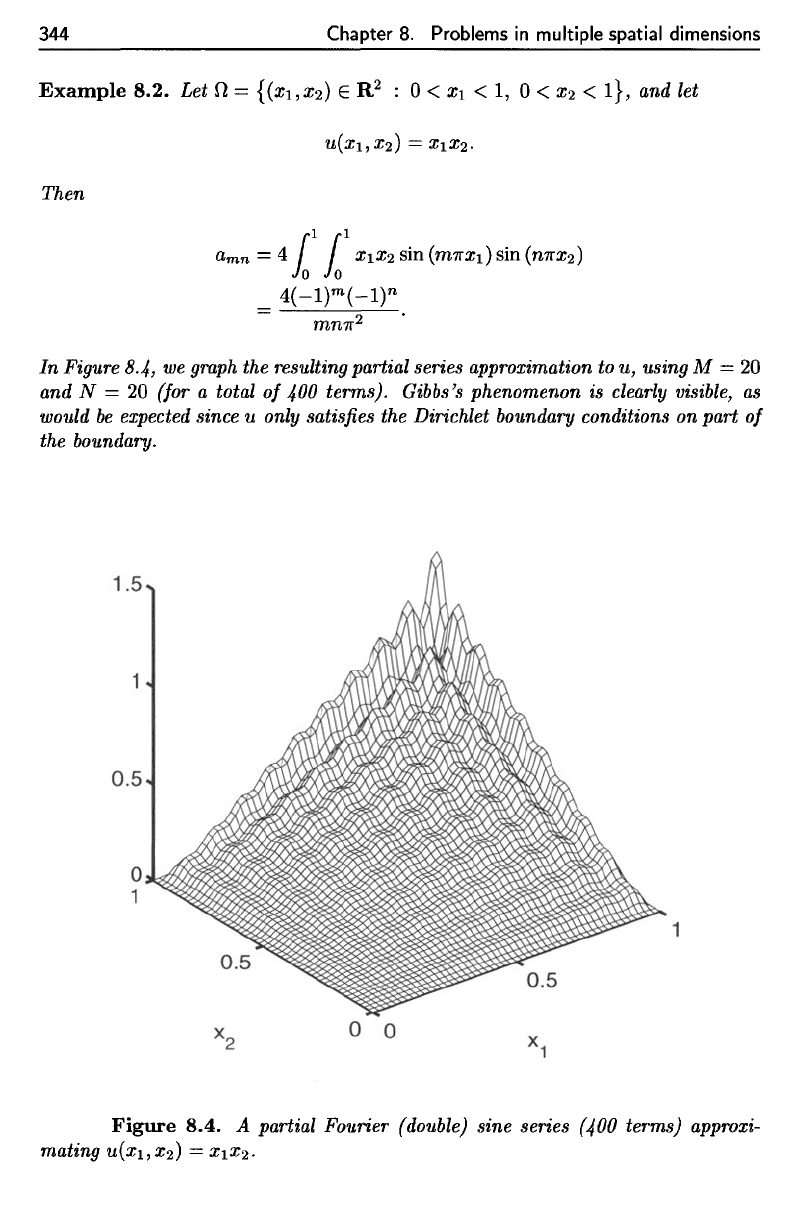
Figure 8.4.

A

partial Fourier

(double)

sine series

(400

terms)

approxi-

mating

ll(xi,X2)

=

XiX-2.

Example

8.2.

Let

Q

=

{(xi,x

2

)

e

R

2

: 0 <

xi

< 1, 0 <

x

2

<

l},

and let

Then

344

Chapter

8.

Problems

in

multiple spatial dimensions

Example

8.2.

Let n = {(X1,X2) E

R2

: 0 <

Xl

< 1, 0 <

X2

<

I},

and let

Then

a

mn

=

410

1

10

1

X1X2

sin

(mnx1)

sin

(nnx2)

4(-1)m(-1)n

mnn

2

In

Figure 8.4, we gmph the resulting partial series approximation to

u,

using M =

20

and

N = 20 (for a total

of

400 terms). Gibbs's

phenomenon

is clearly visible, as

would

be

expected since u only satisfies the Dirichlet boundary conditions on part

of

the boundary.

1.5

1

0.5

o

1

o 0

Figure

8.4.

A partial Fourier (double) sine series (400 terms) approxi-

mating U(X1,X2)

=

X1X2.

8.2. Fourier series

on a

rectangular domain

345

8.2.2 Solving

a

boundary value problem

It is no

more

difficult

to

apply

the

Fourier series method

to a BVP in two or

three

dimensions

than

it was in one

dimension, provided,

of

course,

that

we

know

the

eigenvalues

and

eigenfunctions.

Example

8.3.

We

will

solve

the

following

BVP:

where

£1

is the

unit square:

We

first

write

the

constant function

/(x)

= 1 as a

Fourier sine series.

We

have

where

We

next write

the

solution

u

as

It is

straightforward

to

show that, since

u

satisfies

homogeneous Dirichlet conditions,

where

(see

Exercise

8). The PDE

therefore

implies that

and

therefore

8.2. Fourier

series

on

a rectangular domain 345

8.2.2

Solving

a boundary value problem

It

is no more difficult

to

apply

the

Fourier series method

to

a

BVP

in two

or

three

dimensions

than

it

was in one dimension, provided, of course,

that

we

know the

eigenvalues

and

eigenfunctions.

Example

8.3.

We will solve the following

BVP:

-~U

= 1 in

n,

(8.19)

U = 0 on

an,

where n is the

unit

square:

We first write the constant junction

f(x)

= 1

as

a Fourier sine series. We have

where

00

1 = L L C

mn

sin

(m1fxd

sin (

n1fX

2),

m=l n=l

C

mn

=

411

11

sin

(m1fxd

sin (n1fX2)

dX2

dX1

4((-1)n(-1)m

-

(_l)n

-

(_l)m

+

1)

mn1f

2

We

as

00

U(X1,X2) = L L a

mn

sin (

m1fX

1)

sin (n1fX2).

m=ln=l

It

is straightforward to show that, since U satisfies homogeneous Dirichlet conditions,

00

-~U(X1,X2)

= L

LAmnamnsin(m1fxdsin(n1fx2),

m=l n=l

where

Amn =

(m

2

+n2)1f2,

m,n

=

1,2,3,

...

(see Exercise 8). The

PDE

therefore implies that

00

00 00

L L Amnamn sin

(m1fxd

sin (

n1fX

2)

= L L C

mn

sin

(m1fxd

sin (

n1fX

2),

m=l n=l m=l n=l

and therefore

Amnamn = C

mn

' m, n =

1,2,3,

....

346

Chapter

8.

Problems

in

multiple

spatial dimensions

This

in

turn

implies that

In

Figure 8.5,

we

graph

the

partial Fourier series with

M

— 10, N = 10.

Figure

8.5.

The

solution

to the BVP

(8.19),

approximated

by a

Fourier

series with

100

terms.

8.2.3 Time-dependent problems

It is

also straightforward

to

extend

the

one-dimensional Fourier series techniques

for

time-dependent problems

to

two-

or

three-dimensional problems, again assuming

that

eigenvalues

and

eigenfunctions

are

known.

We

illustrate

with

an

example.

Example

8.4.

We

will

solve

the

following

IBVP

for the

wave

equation

on the

unit

square:

We

can

approximate

the

solution

by a

partial Fourier series

of the

form

346

Chapter

8.

Problems

in

multiple spatial dimensions

This

in

turn implies that

We

can approximate the solution

by

a partial Fourier series

of

the form

M N

L L a

mn

sin (m1rxt) sin (

n1rX

2).

m=l

n=l

In Figure 8.5,

we

graph

the partial Fourier series with M = 10, N = 10.

1

o 0

x,

Figure

8.5.

The solution to the

BVP

(8.19), approximated

by

a Fourier

series with 100 terms.

8.2.3 Time-dependent

problems

It

is

also straightforward

to

extend

the

one-dimensional Fourier series techniques

for time-dependent problems

to

two- or three-dimensional problems, again assuming

that

eigenvalues and eigenfunctions are known.

We

illustrate with an example.

Example

8.4.

We will solve the following

IBVP

for the wave equation on the unit

square:

cPu

{)t

2

-

c

2

du

= 0, x E

n,

t > 0,

8.2. Fourier

series

on a

rectangular domain

347

The

initial

velocity

function

will

be

taken

to be the

function

We

take

c =

261V5.

This

IBVP

models

a

(square)

drum struck

by a

square

hammer.

We

write

the

solution

u

as

where

The

PDE

then takes

the

form

where

X

mn

= (m

2

+n

2

)7r

2

.

The

initial conditions

become

and

We

have

where

8.2. Fourier

series

on

a rectangular domain

u(x,O) = 0, x E

n,

au

at

(x,

0)

= ,,((x), x E

n,

u(x, t) =

0,

x E

an,

t >

O.

The

initial velocity function will

be

taken

to

be

the function

(x) =

-,

5 <

Xl

<

5'

5 <

X2

<

5'

{

1

2 3 2 3

"(

0, otherwise.

347

(8.20)

We

take c = 261.;2. This IBVP models a (square) drum struck

by

a

square

hammer.

We

write the solution u

as

00

U(XI,X2,t) = L

Lamn(t)sin(m7fxdsin(n7fX2),

m=l

n=1

where

amn(t) =

410

1

10

1

U(Xl>X2,t)

sin

(m7fXI)

sin

(n7fX2)

dX2

dx

1

.

The

PDE then takes the form

~

{

~~r;n

(t) + c

2

Amnamn(t)} sin

(m7fX1)

sin

(n7fX2)

= 0,

where

Amn

= (m

2

+ n

2

)7f2.

The

initial conditions

become

00

U(X1,X2,0) = L L

amn(O)

sin (

m7fX

1)

sin (

n7fX

2)

= 0

m=1

n=l

and

We

have

where

00 00

"((X1,X2)

= L L bmnsin

(m7fxt}

sin (

n7fX

2),

m=l

n=l

b

mn

=

410

1

10

1

"((X1,X2)

sin (m7fxt) sin

(n7fX2)

dX2 dX1

=

-4

[3/5 [3/5 sin (m7fxd sin (

n7fX

2)

dX2

dx

1

12/5 12/5

4(cos

(3n7f

/5) -

cos

(2n7f

/5)(cos

(3m7f

/5) -

cos

(2m7f

/5))

mn7f

2

Gockenbach M.S. Partial Differential Equations. Analytical and Numerical Methods

Подождите немного. Документ загружается.