Gockenbach M.S. Partial Differential Equations. Analytical and Numerical Methods
Подождите немного. Документ загружается.


328
Chapter
8.
Problems
in
multiple
spatial dimensions
8.1.1
The
divergence
theorem
An
advantage
of
using vector
notation
is
that
many results
of
calculus take
the
same
form
for two and
three dimensions when expressed
in
vector
form.
Therefore,
we
will
treat
both two-dimensional
and
three-dimensional problems
in
this section,
and
much
of the
background calculus requires
no
distinction between
R
2
and
R
3
.
Let
f2
be a
domain
(a
connected open set)
in
R
2
or
R
3
with
a
piecewise
smooth boundary
<9fi.
50
We
will
denote points
in
R
3
using either vector notation
or
coordinate notation
as is
convenient,
and
similarly
for
points
in
R
2
.
Thus
a
point
in
R
3
can be
denoted
as x or as
(xi,X2,xs).
An
important concept related
to a
domain
fi is
that
of the
(outward) unit
normal.
At
each point
x of
dfl
at
which
the
boundary
is
smooth, there
is a
unique
unit
vector n(x)
that
is
orthogonal
to
dtl
at x (to be
precise, n(x)
is
orthogonal
to the
line
or
plane
tangent
to
dft
at x) and
points toward
the
exterior
of fi. It
is
customary
to
suppress
the
dependence
of the
normal vector
n on x,
writing
n
instead
of
n(x),
but it is
important
to
keep this dependence
in
mind. Figure
8.1
shows
an
example
in two
dimensions.
Figure
8.1.
A
two-dimensional domain
J7
with
a
sample
unit normal vector.
A
(volume) integral over
fJ
in
R
3
will
be
denoted
as
or
simply
by
50
For
our
purposes,
it
does
not
seem worthwhile
to
define
precise conditions
on fi and its
bound-
ary
that
allow
the
application
of the
divergence theorem.
We
will assume
that
the
reader
has an
intuitive idea
of the
meaning
of
"smooth boundary"
and
"piecewise smooth boundary."
For
exam-
ple,
the
unit ball,
S =
{(xi,X2,xs)
G
R
3
:
x
2
+
y
2
+ z
2
< 1
j,
has a
smooth boundary, while
the
unit
cube,
R =
{(xi,X2,xz)
e
R
3
: 0
<
x\
<
1,0
<
#2
<
1,0
<
#3
<
ij,
has a
boundary
that
is
piecewise
smooth.
328
Chapter
8.
Problems
in
multiple spatial dimensions
B.1.1 The divergence theorem
An advantage of using vector notation
is
that
many results of calculus take
the
same form for two and three dimensions when expressed in vector form. Therefore,
we
will
treat
both two-dimensional
and
three-dimensional problems in this section,
and
much of the background calculus requires no distinction between R2
and
R3.
Let 0 be a domain (a connected open set) in
R2
or
R3
with a piecewise
smooth boundary
80.
50
We
will denote points in
R3
using either vector notation
or coordinate notation
as
is
convenient, and similarly for points in R2. Thus a point
in
R3
can be denoted as x or as
(Xl,X2,X3).
An important concept related
to
a domain 0
is
that
of the (outward) unit
normal.
At each point x of
80
at
which
the
boundary
is
smooth, there is a unique
unit vector
n(x)
that
is
orthogonal
to
80
at
x (to be precise,
n(x)
is
orthogonal
to
the
line or plane tangent
to
80
at
x) and points toward the exterior of
O.
It
is
customary to suppress
the
dependence of
the
normal vector n on
x,
writing n
instead of
n(x),
but
it
is
important
to
keep this dependence in mind. Figure
8.1
shows
an
example in two dimensions.
nix)
Figure
8.1.
A two-dimensional domain 0 with a sample unit normal vector.
A (volume) integral over 0 in
R3
will be denoted
as
In
f(x)dx
or simply by
SOFor
our
purposes,
it
does
not
seem worthwhile
to
define precise conditions
on
n
and
its
bound-
ary
that
allow
the
application
of
the
divergence theorem. We will assume
that
the
reader
has
an
intuitive idea
of
the
meaning
of
"smooth
boundary"
and
"piecewise
smooth
boundary."
For
exam-
ple,
the
unit
ball, S = {(Xl,
X2,
X3)
E
R3
:
X2
+
y2
+
z2
<
I},
has a
smooth
boundary, while
the
unit
cube, R = {(Xl,
X2,
X3)
E
R3
:
O:S
Xl
:S
1,0
:S
X2
:S
1,0
:S
X3
:S
I},
has a
boundary
that
is
piecewise
smooth.

8.1. Physical models
in two or
three spatial dimensions
329
where
/ :
£)
->
R. If a
domain
£)
in
R/
5
can be
described
as
for
example, then
the
volume integral
can be
rewritten
as an
iterated integral:
A
(surface)
integral over
<9fJ
will
be
denoted
by
where
g
:
d£l
—»•
R and da
represents
an
infinitesimal surface
area
element,
or
simply
Both volume
and
surface integrals
can
have
vector-valued
integrands,
in
which case
each component
is
integrated.
If
Jl
is a
domain
in
R
2
,
then
is
an
area
integral
that
can,
for
many regions
fi, be
rewritten
as a
doubly
iterated
integral.
Since
dQ,
is a
curve
in
this case.
is
a
line
integral.
51
A
vector
field
defined
on
£)
is
just
a
vector-valued
function—a
mapping
of the
form
if
fi is in
R
2
or
if
f)
is in
R
3
.
The
divergence
of a
vector
field f is
denoted
by V • f and is
defined
by
in
two
dimensions
and
51
Line
integral
is a
misnomer, since
the
domain
of
integration
is
generally
a
curve,
not a
(straight)
line.
8.1. Physical models
in
two or three spatial dimensions
329
where f : n
--+
R.
If
a domain n in R3 can be described as
{(Xl,
X2,
X3)
: a <
Xl
<
b,
gl
(xI) < X2 <
g2(XI),
h1
(Xl,
X2)
<
X3
< h
2
(X1,
X2)}
,
for example, then the volume integral can be rewritten as
an
iterated integral:
A (surface) integral over
an
will be denoted by
r g(x)
dO",
i
8
1l
where 9 :
an
--+
R and
dO"
represents
an
infinitesimal surface area. element, or simply
hll
g.
Both volume and surface integrals can have vector-valued integrands, in which case
each component
is
integrated.
If
n
is
a domain in R
2
,
then
is
an
area integral
that
can, for many regions
n,
be rewritten as a doubly iterated
integral. Since
an
is
a curve in this case,
hll
9
is
a line integral.
51
A vector field defined on n
is
just
a vector-valued
function-a
mapping of the
form
f(x) = [
il
(x) ]
hex)
if n
is
in R
2
or
f(x) = [
;~~:j
1
fs(x)
if
n
is
in R
3
.
The divergence of
a.
vector field f
is
denoted by
V'
. f and
is
defined by
ail
ah
V'
. f(x) =
-a
(x) +
-a
(x)
Xl
X2
in two dimensions and
V'
. f(x) =
aa
il
(x) +
aa
h
(x) +
aa
fs
(x)
Xl
X2
X3
51 Line integral is a misnomer, since
the
domain
of
integration is generally a curve,
not
a (straight)
line.

In the
case
of a
rectangular domain
in R
2
, the
divergence theorem
follows
immediately
from
the
fundamental theorem
of
calculus (see Exercise
2).
8.1.2
The
heat
equation
for a
three-dimensional
domain
We
now
consider
a
three-dimensional solid occupying
a
domain
fi
in
R
3
.
(We
will
often
call
the
solid
17,
although,
in
fact,
17 is a
mathematical description
of
the
location
of the
solid.)
For
simplicity, assume
that
the
solid
is
homogeneous,
with
density
p,
specific
heat
c, and
thermal conductivity
K.
Analogous
to the
one-
dimensional case,
if the
domain
a;
is a
subset
of 17,
then
the
total
heat energy
contained
in
o>
is
330
Chapter
8.
Problems
in
multiple spatial dimensions
in
three dimensions.
The
following
theorem, which holds
in
both
two and
three
dimensions,
explains
why
this combination
of
derivatives
is so
significant.
Theorem
8.1. (The
divergence
theorem)
Let 17 be a
bounded
open
set
with
a
piecewise
smooth
boundary
$17.
Assume that
f is a
smooth vector
field
defined
on
17
U
d£l,
and
that
n is the
(outward
pointing) unit normal
to
017.
Then
where
w(x,t)
is the
temperature
at x 6 17 at
time
i,
T
0
is the
reference
temperature,
and
EQ
is the
thermal energy contained
in the
solid
at
temperature
T
0
.
The
rate
of
change
of the
energy contained
in
u;
is
given
by
Moving
the
derivative through
the
integral sign,
we
obtain
the
following
expression
for
the
rate
of
change
of
total
heat
energy
contained
in
uj:
We
can
also describe this
rate
of
change
by
computing
the
rate
at
which
heat
energy
flows
across
duj.
Let
q(x,£)
€
R
3
be the
heat
flux at x
e
17 at
time
t. The
heat
flux is a
vector—its
direction
is the
direction
of the flow of
energy,
and its
magnitude gives
the
rate
at
which energy
is flowing
across
the
plane
at x to
which
q(x,
£)
is
orthogonal,
in
units
of
energy/(time-area).
At
each point
of
duj,
the
rate
at
which energy
is flowing
into
u;
is
(This
follows
from
the
fact
that
q is a
vector quantity
and
hence
can be
decomposed
into
the
component
in the
direction
of
—n,
which
is
—q
• n, and the
component
330
Chapter
8.
Problems
in
multiple spatial dimensions
in three dimensions.
The
following theorem, which holds in both two and three
dimensions, explains why this combination of derivatives is so significant.
Theorem
8.1.
(The
divergence
theorem)
Let n
be
a bounded open set with a
piecewise smooth boundary
an.
Assume that f is a smooth vector field defined on
n u
an,
and that n
is
the (outward pointing) unit normal to
an.
Then
r
\7
. f = r
f·
n.
in
ian
In
the
case of a rectangular domain in R
2
,
the divergence theorem follows
immediately from the fundamental theorem of calculus (see Exercise 2).
8.1.2
The
heat equation for a three-dimensional domain
We
now consider a three-dimensional solid occupying a domain n in R
3
.
(We
will often call the solid
n,
although, in fact, n
is
a mathematical description of
the
location of
the
solid.) For simplicity, assume
that
the solid
is
homogeneous,
with density
p, specific heat
c,
and thermal conductivity
K,.
Analogous
to
the one-
dimensional case,
if
the domain w
is
a subset of
n,
then the
total
heat energy
contained in
w
is
Eo
+ L pc(u(x, t) -
To)
dx,
where
u(x,
t) is
the
temperature
at
x E n
at
time t,
To
is
the
reference temperature,
and
Eo
is
the
thermal energy contained in
the
solid
at
temperature
To.
The rate of change of the energy contained in w
is
given by
!
[Eo
+ L pc(u(x, t) -
To)
dX]
= ! L pcu(x, t) dx.
Moving
the
derivative through
the
integral sign,
we
obtain the following expression
for
the
rate
of change of total heat energy contained in
w:
r
au
iw
pc
at
(x, t) dx.
(8.1)
We
can also describe this rate of change by computing
the
rate
at
which heat
energy
flows
across
ow.
Let
q(x,
t) E
R3
be
the
heat flux
at
x E n
at
time t. The
heat flux
is
a
vector-its
direction
is
the
direction of the
flow
of energy, and its
magnitude gives the
rate
at
which energy
is
flowing across the plane
at
x
to
which
q(x,
t)
is
orthogonal, in units of energy /(time·area). At each point of
ow,
the
rate
at
which energy
is
flowing into w is
-q-n.
(This follows from the fact
that
q is a vector quantity and hence can be decomposed
into the component in
the
direction of
-n,
which
is
-q
.
n,
and
the
component

8.1. Physical models
in two or
three spatial dimensions
331
We
now
make
the
assumption called Fourier's law,
that
the
heat
flux is
pro-
portional
to the
temperature
gradient:
52
We
wish
to
equate this expression with (8.1)
and
derive
a
PDE.
To do so, we
must
apply
the
divergence theorem
to
convert
the
boundary
integral
to a
volume
integral:
52
The
gradient
of a
scalar-valued
function
of
several
variables points
in the
direction
in
which
the
function
increases most rapidly.
orthogonal
to
—
n.) The
total
amount
of
energy
flowing
into
uj
is
then
The
constant
of
proportionality,
K
> 0, is the
thermal conductivity, just
as in one
spatial
dimension.
We
therefore obtain
the
following
expression
for the
rate
of
change
of
heat energy contained
in
a;:
We
thus have
or
Since
(8.2) holds
for
every
subdomain
uj
of
£),
by
exactly
the
same reasoning
as in one
dimension,
the
integrand must
be
identically zero.
We
therefore obtain
the PDE
The
combination
V • V of
differential
operators arises
frequently
due to
just such
an
application
of the
divergence theorem.
We
have
8.1. Physical models
in
two or three spatial dimensions
331
orthogonal
to
- n.) The
total
amount of energy flowing into w
is
then
- r
q.n.
Jaw
We
now make
the
assumption called Fourier's law,
that
the heat flux
is
pro-
portional
to
the temperature gradient:
52
q(x, t) = -1\;\7u(x, t).
The constant of proportionality,
I\;
> 0,
is
the
thermal conductivity,
just
as
in one
spatial dimension.
We
therefore obtain
the
following expression for
the
rate
of
change of heat energy contained in
w:
We
wish
to
equate this expression with (8.1) and derive a PDE. To do so,
we
must
apply
the
divergence theorem
to
convert
the
boundary integral
to
a volume integral:
We
thus have
i
pc
~~
(x, t)
dx
= i
1\;\7
.
\7u(x,
t) dx,
or
i
(pc
~~
(x, t) -
1\;\7
. \7u(x,
t))
dx
=
O.
(8.2)
Since (8.2) holds for every subdomain
w of
n,
by exactly the same reasoning
as
in one dimension, the integrand must
be
identically zero.
We
therefore obtain
the
PDE
au
pc
at
-
1\;\7
.
\7u
= 0, x E
n,
t >
to·
The combination
\7
.
\7
of differential operators arises frequently due
to
just
such
an application of the divergence theorem.
We
have
[
gx~
1
\7u =
~:
'
aX3
52
The
gradient
of
a scalar-valued function of several variables
points
in
the
direction in which
the
function increases most rapidly.

332
Chapter
8.
Problems
in
multiple
spatial dimensions
and so
53
Another common symbol
for the
Laplacian
is
V
2
.
The
differential
operator
is
called
the
Laplacian.
53
Using
this notation,
we
obtain
the
three-dimensional heat
equation:
If
/ :
fi
x
(to,
00}
->•
R is a
heat source
(or
sink),
with units
of
energy
per
volume
per
time, then
we
obtain
the
inhomogeneous three-dimensional heat equation:
It
should
be
obvious
to the
reader
how to
modify
this equation
if the
material
properties
(p,
c,
K)
are not
constants
but
rather
functions
of x G 0
(see Exercise
1).
8.1.3 Boundary
conditions
for the
three-dimensional
heat
equation
Two
common types
of
boundary conditions
for the
heat equation
are
Dirichlet
and
Neumann
conditions.
An
equation
of the
form
is
called
a
homogeneous Dirichlet condition;
it
corresponds
to an
experiment
in
which
the
temperature
of the
boundary
is
held
fixed at 0.
Inhomogeneous Dirichlet
conditions
are
also possible,
and
boundary
data
can be
time-dependent:
It is
also possible
to
insulate
the
boundary, which leads
to the
condition
that
the
heat
flux
across
the
boundary
is
zero:
The
directional derivative
Vw
• n is
often
referred
to as the
normal
derivative
and
denoted
332
Chapter
8.
Problems
in
multiple
spatial
dimensions
and
so
The
differential
operator
8
2
8
2
a
2
6.=8
2
+8
2
+a
2
Xl
X
2
X3
is
called
the
Laplacian.
53
Using this
notation,
we
obtain
the
three-dimensional
heat
equation:
au
pc
8t
- ",6.u =
0,
x E
.11,
t >
to·
(8.3)
If
f : n x
(to,
00)
-+
R
is
a
heat
source (or sink),
with
units
of
energy
per
volume
per
time,
then
we
obtain
the
inhomogeneous three-dimensional
heat
equation:
8u
pc
8t
- ",6.u =
f(x,
t), x E
.11,
t>
to·
(8.4)
It
should
be
obvious
to
the
reader
how
to
modify this
equation
if
the
material
properties
(p,
c,
"') are
not
constants
but
rather
functions of x E n (see Exercise 1).
8.1.3 Boundary conditions for the three-dimensional heat
equation
Two common types of
boundary
conditions for
the
heat
equation
are
Dirichlet
and
Neumann
conditions.
An
equation
of
the
form
u = ° on
an
is called a homogeneous Dirichlet condition;
it
corresponds
to
an
experiment in
which
the
temperature
of
the
boundary
is held fixed
at
o.
Inhomogeneous Dirichlet
conditions
are
also possible,
and
boundary
data
can
be time-dependent:
u(x, t) = g(x), x E
8n,
t > to,
or
u(x, t) = g(x, t), x E
an,
t >
to.
It
is
also possible
to
insulate
the
boundary, which leads
to
the
condition
that
the
heat
flux across
the
boundary
is zero:
\7u(x,
t)
. n = 0, x E
an,
t >
to.
The
directional derivative
\7
u . n
is
often referred
to
as
the
normal derivative
and
denoted
au
an·
53
Another
common symbol for
the
Laplacian is
'\7
2
•

8.1.
Physical
models
in two or
three spatial
dimensions
333
Just
as in the
one-dimensional case,
we can
have mixed boundary conditions,
since
it is
possible
to
treat
different
parts
of the
boundary
differently.
Suppose
dtl
=
FI
U
F2
is a
partition
of the
boundary into
two
disjoint sets. Then
it is
possible
to
pose
a
problem with
the
following
mixed boundary conditions:
8.1.4
The
heat equation
in a bar
In
Section
2.1
and in
subsequent sections,
we
discussed
heat
flow in a bar
with insu-
lated sides.
We
mentioned
the
following
fact:
If the
initial temperature distribution
in
a bar
depends only
on the
longitudinal coordinate
(that
is, if it is
constant
in
each cross-section),
and if any
heat source also depends only
on the
longitudinal
coordinate, then
the
temperature
at all
subsequent times also depends only
on a
single
spatial
coordinate.
We can now
justify
this statement.
Let
the
domain
ft in R
3
be
defined
by
where
i
and r are
given positive constants.
The set
fHs
a
circular cylinder centered
on
the
interval
[0,^1
on the
xi-axis.
Consider
the
following
IBVP:
where
F
e
represents
the
ends
of the bar and
T
t
the
transverse sides:
The
reader should notice
that
both
the
heat
source
/ and the
initial
temperature
distribution
if)
are
independent
of
x-2
and
x
3
.
The
solution
to
(8.5)
is
w(xi,x
2
,x
3
,i)
=
v(xi,t),
where
v is the
solution
of
the
IBVP
The
proof
of
this
is a
direct verification
of the
equations
in
(8.5)
and is
left
to an
exercise.
8.1. Physical models
in
two or three spatial dimensions
333
Just
as in
the
one-dimensional case,
we
can have mixed boundary conditions,
since
it
is
possible to
treat
different
parts
of the boundary differently. Suppose
an
= r
l
U r
2
is
a partition of the boundary into two disjoint sets.
Then
it
is
possible
to
pose a problem with
the
following mixed boundary conditions:
u(x,t)
= 0, x E
rl,
t >
to,
au
an
(x, t) = 0, x E r
2
,
t >
to·
8.1.4 The heat equation
in
a
bar
In
Section
2.1
and in subsequent sections,
we
discussed
heat
flow
in a
bar
with insu-
lated sides.
We
mentioned
the
following fact:
If
the initial temperature distribution
in a
bar
depends only on the longitudinal coordinate
(that
is,
if
it
is constant in
each cross-section), and if any heat source also depends only on
the
longitudinal
coordinate,
then
the temperature
at
all subsequent times also depends only on a
single spatial coordinate.
We
can now justify this statement.
Let
the
domain n in R
3
be defined by
n = {(XI,X2,X3) : ° <
Xl
<
l,
x~
+x~
<
r2},
where l and r are given positive constants.
The
set n is a circular cylinder centered
on
the
interval
[0,
l]
on the
Xl
-axis. Consider the following IBVP:
au
pc
at
- ",flu = I(Xl, t), x En,
t>
to,
u(x,
to)
= '¢(xt), x E
n,
au
an
(x, t) = 0, x E
rt,
t>
to,
u(x,t)
= 0, x
Ere,
t > to,
where r e represents the ends of
the
bar
and r t the transverse sides:
re
= {(O,X2,X3) :
x~
+x§
< r2} U {(f,X2,X3) :
x~
+x§
<
r2},
r
t
={(Xl,X2,X3):
O<xl<l,
x~+x~=r2}.
(8.5)
The
reader should notice
that
both
the
heat
source I and the initial temperature
distribution
'¢ are independent of
X2
and
X3.
The solution to (8.5)
is
U(Xl,X2,X3,t) = V(Xl,t), where v
is
the solution of
the
IBVP
OV
02V
pc--;:;-
-
"'>:.
2 =
I(Xl,t),
° <
Xl
<
l,
t>
to,
ut
uX
l
V(XI,
to)
=
'¢(xd,
° <
Xl
<
l,
V(O,
t) = 0, t > to,
v(i, t) = 0, t > to.
(8.6)
The
proof of this
is
a direct verification of the equations in (8.5) and
is
left to
an
exercise.

334
Chapter
8.
Problems
in
multiple spatial dimensions
8.1.5
The
heat
equation
in two
dimensions
It is
straightforward
to
restrict
the
heat equation
to two
dimensions.
If
heat
flows in
a
solid, such
as a
thin plate,
in
such
a way
that
the
temperature
is
constant
in one
dimension,
the
derivative with respect
to the
third spatial variable,
say
#3,
vanishes.
The
result
is the
two-dimensional
heat
equation, which
is
usually written exactly
as in
(8.3), since
we
will
also
use A to
denote
the
Laplacian
in two
independent
variables:
The
distinction between
the
two-
and
three-dimensional Laplacian
will
be
under-
stood
from
context.
8.1.6
The
wave
equation
for a
three-dimensional
domain
The
derivation
of the
wave equation
in
three dimensions
is
considerably more com-
plicated
than
that
of the
heat equation.
A
complete treatment begins with
an
elastic
solid,
and
applies Newton's
law to the
forces,
both internal
and
external, acting
on
the
solid.
The
result
is a
system
of
three (coupled) PDEs
for the
three components
of
displacement
that
describes
the
vibration
of the
solid. (Each point
in the
solid
can
move
in
three dimensions,
so
there
are
three dependent variables.) This system
is
one
form
of the
wave equation.
Much
useful
physical modeling
can be
performed under apparently severe sim-
plifying
assumptions.
Specifically,
assuming
that
the
solid
is a fluid
(meaning
that
the
only stress supported
is a
pressure)
and
that
the
motion under consideration
is
a
small perturbation
of an
equilibrium
state,
with
the
motion induced
by a
force
density
F(x,
£),
the
result
is the
acoustic
wave
equation
for the
pressure perturbation
u
=
u(x.t):
In
this equation,
the
forcing
function
/ is the
negative divergence
of the
body
force:
An
example
of a
physical phenomenon modeled
by the
three-dimensional acoustic
wave
equation
is the
propogation
of
sound waves
in
air.
8.1.7
The
wave
equation
in two
dimensions
The
two-dimensional (acoustic) wave equation models
the
small transverse vibra-
tions
of an
elastic
membrane.
An
elastic
membrane
is
analogous
to an
elastic
string,
in
that
it
does
not
resist bending.
The
form
of the
wave equation
is
exactly
as in
(8.7);
however,
the
meaning
is
quite
different.
The
dependent variable
u is the
vertical component
of
displacement, while
the
right-hand side
/ is the
transverse
pressure. Figure
8.2
illustrates
the
small
deflection
of a
square membrane.
334
Chapter
8.
Problems
in
multiple spatial dimensions
8.1.5 The heat equation
in
two
dimensions
It
is
straightforward
to
restrict the heat equation to two dimensions.
If
heat
flows
in
a solid, such as a thin plate, in such a way
that
the temperature is constant in one
dimension,
the
derivative with respect
to
the
third spatial variable, say
X3,
vanishes.
The result
is
the two-dimensional heat equation, which
is
usually written exactly
as in (8.3), since
we
will also use A
to
denote the Laplacian in two independent
variables:
The distinction between the two-
and
three-dimensional Laplacian will be under-
stood from context.
8.1.6
The
wave equation for a three-dimensional domain
The derivation of the wave equation in three dimensions is considerably more com-
plicated
than
that
of the heat equation. A complete treatment begins with an elastic
solid,
and
applies Newton's law
to
the
forces, both internal
and
external, acting on
the solid.
The
result is a system of three (coupled) PDEs for the three components
of displacement
that
describes
the
vibration of
the
solid. (Each point in the solid
can move in three dimensions,
so
there are three dependent variables.) This system
is
one form of
the
wave equation.
Much useful physical modeling can be performed under apparently severe sim-
plifying assumptions. Specifically, assuming
that
the solid
is
a fluid (meaning
that
the
only stress supported
is
a pressure) and
that
the motion under consideration
is
a small perturbation of an equilibrium state, with the motion induced by a force
density
F(x,
t),
the
result
is
the acoustic wave equation for the pressure perturbation
u =
u(x,
t):
(8.7)
In this equation, the forcing function f
is
the
negative divergence of the body force:
f(x,
t) = - \7 .
F(x,
t).
An example of a physical phenomenon modeled by
the
three-dimensional acoustic
wave equation is the propogation of sound waves in air.
8.1.7 The
wave
equation
in
two
dimensions
The two-dimensional (acoustic) wave equation models
the
small transverse vibra-
tions of
an
elastic membrane. An elastic membrane is analogous
to
an elastic string,
in
that
it does not resist bending. The form of the wave equation
is
exactly as in
(8.7); however,
the
meaning
is
quite different. The dependent variable u
is
the
vertical component of displacement, while the right-hand side
f
is
the transverse
pressure. Figure 8.2 illustrates
the
small deflection of a square membrane.
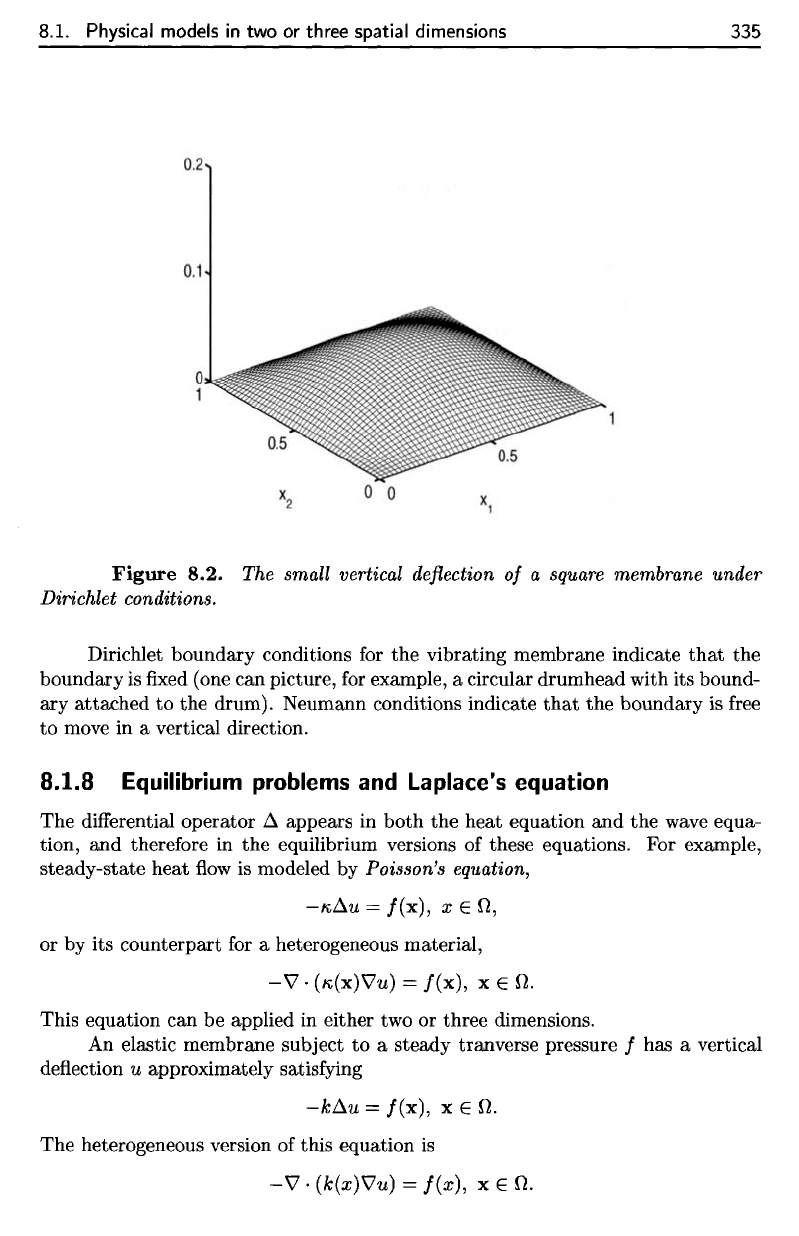
8.1. Physical models
in two or
three spatial dimensions
335
Figure
8.2.
The
small vertical
deflection
of a
square
membrane under
Dirichlet
conditions.
Dirichlet
boundary conditions
for the
vibrating membrane indicate
that
the
boundary
is fixed
(one
can
picture,
for
example,
a
circular drumhead with
its
bound-
ary
attached
to the
drum).
Neumann conditions
indicate
that
the
boundary
is
free
to
move
in a
vertical direction.
8.1.8 Equilibrium problems
and
Laplace's
equation
The
differential
operator
A
appears
in
both
the
heat
equation
and the
wave equa-
tion,
and
therefore
in the
equilibrium versions
of
these equations.
For
example,
steady-state
heat
flow is
modeled
by
Poisson's equation,
or
by its
counterpart
for a
heterogeneous material,
This equation
can be
applied
in
either
two or
three dimensions.
An
elastic membrane subject
to a
steady
tr
an
verse pressure
/ has a
vertical
deflection
u
approximately satisfying
The
heterogeneous version
of
this equation
is
8.1. Physical models
in
two or three spatial dimensions
335
0.1
o 0
Figure
8.2.
The small vertical deflection
of
a square membrane under
Dirichlet conditions.
Dirichlet boundary conditions for the vibrating membrane indicate
that
the
boundary
is
fixed (one can picture, for example, a circular drumhead with its bound-
ary attached
to
the drum). Neumann conditions indicate
that
the
boundary
is
free
to move in a vertical direction.
8.1.8 Equilibrium problems
and
Laplace's equation
The differential operator
~
appears in
both
the
heat equation and the wave equa-
tion, and therefore in the equilibrium versions of these equations. For example,
steady-state
heat
flow
is modeled by Poisson's equation,
-K,~u
=
f(x),
x E
n,
or by its counterpart for a heterogeneous material,
-~.
(K,(x)~u)
=
f(x),
x E
n.
This equation can be applied in either two or three dimensions.
An elastic membrane subject to a steady tranverse pressure f has a vertical
deflection
u approximately satisfying
-k~u
=
f(x),
x E
n.
The heterogeneous version of this equation
is
-~.
(k(x)~u)
=
f(x),
x E
n.

336
Chapter
8.
Problems
in
multiple
spatial
dimensions
The
homogeneous version
of
Poisson's equation
is
referred
to as
Laplace's
equation:
Of
course,
this
equation
is
interesting only
if the
boundary conditions
are
inhomo-
geneous.
8.1.9
Green's
identities
and the
symmetry
of the
Laplacian
We
should expect
to be
able
to
extend
the
methods
from
the
preceding chapters
only
if
—A
is a
symmetric operator.
The
inner product
is
and we
must
show
that
for
all
u,v
satisfying
the
desired boundary conditions.
We
define
(7
2
(J7)
=
{w:(]->R
: u and its
partial
derivatives
up to
order
2 are
continuous}
(£1
is the
closure
of
Q,
that
is, fi
together with
its
boundary:
J7
=
i7
U
9fi)
and
and
In one
dimension,
the
fundamental manipulation underlying
the
development
of
both Fourier series
and finite
element methods
is
integration
by
parts.
The
ana-
logue
in
higher dimensions
is
Green's
(first)
identity,
which
we now
derive.
It is
helpful
to
recall
that
integration
by
parts
is
based
on the
product rule
for
differen-
tiation
and the
fundamental theorem
of
calculus,
as
follows:
To
derive Green's identity,
we
need
an
analogous product rule
for
higher dimensions
336
Chapter
8. Problems
in
multiple spatial dimensions
The homogeneous version of Poisson's equation
is
referred
to
as Laplace's
equation:
-~u
=
0,
x
EO.
Of course, this equation is interesting only
if
the boundary conditions are inhomo-
geneous.
8.1.9 Green's identities and the symmetry
of
the Laplacian
We
should expect
to
be able
to
extend
the
methods from the preceding chapters
only if
-~
is a symmetric operator.
The
inner product
is
(f,g)
=
In
fg,
and
we
must show
that
(-~u,v)
=
(u,-~v)
for all u, v satisfying
the
desired boundary conditions.
We
define
c
2
(n) =
{u
: n
-+
R : u and its partial derivatives up to order 2 are continuous}
(n
is the closure of
0,
that
is, 0 together with its boundary: n = 0 u
ao)
and
cb(n)
=
{u
E C
2
(n)
: x E
ao
=?
u(x)
=
o}
and
LD :
cb(n)
-+
C(O),
LDu
=
-~u.
In one dimension,
the
fundamental manipulation underlying the development
of
both
Fourier series and finite element methods
is
integration by parts. The ana-
logue in higher dimensions is Green's (first) identity, which
we
now derive.
It
is
helpful
to
recall
that
integration by parts is based on the product rule for differen-
tiation and
the
fundamental theorem of calculus, as follows:
d
dv
du
dx
[u(x)v(x)] = u(x)
dx
(x) +
dx
(x)v(x)
r
b
d r
b
dv
r
b
du
=?
fa
dx
[u(x)v(x)]
dx
=
fa
u(x)
dx
(x)
dx
+
fa
dx
(x)v(x)
dx
r
b
dv
r
b
du
=? u(x)v(x)l: =
fa
u(x)
dx
(x)
dx
+
fa
dx (x)v(x) dx
l
b
dv
lb
du
=? a
U(X)
dx
(x)
dx
= u(x)v(x)l: - a
dx
(x)v(x)
dx.
To derive Green's identity,
we
need an analogous product rule for higher dimensions.

8.1.
Physical models
in two or
three
spatial dimensions
337
It is not
completely obvious
how to
obtain
the
needed product rule,
but we
can
be
guided
by the
fact
that
we
want
to
obtain
a
formula
involving
The
desired product rule
is
This
is
proved directly;
see
Exercise
5.
Combining (8.8) with
the
divergence theorem
gives
the
desired result:
This
is
Green's
first
identity:
We
can now
prove
the
symmetry
of the
Laplacian under Dirichlet conditions.
If
w,v€
07^(0),
then
It is no
more
difficult
to
prove
the
symmetry
of
—A
under Neumann conditions
(see
Exercise
6).
Exercises
1. How
does
the
heat
equation (8.3) change
if
p,
c,
and
K
are
functions
of x?
8.1. Physical models
in
two or three spatial dimensions
337
It
is
not completely obvious how to obtain the needed product rule,
but
we
can be guided by the fact
that
we
want to obtain a formula involving
v~u
= v\7 . \7u.
The desired product rule
u;
\7 . (v\7u) =
\7u·
\7v +
vAu.
(8.8)
This
is
proved directly; see Exercise
5.
Combining (8.8) with
the
divergence theorem
gives the desired result:
\7 . (v\7u) =
\7u·
\7v +
vAu
=>
l
\7.
(v\7u) = l
\7u·
\7v + l
vAu
=>
{
v\7u·
n = {
\7u·
\7v + r
v~u
ian
in in
=>
{
vAu
= r
vaau
- {
\7u·
\7v.
in
ian
n
in
This is Green's first identity:
{
vAu
= { v
au
- (
\7u·
\7v.
in
ian
an
in
(8.9)
We
can now prove the symmetry of the Laplacian under Dirichlet conditions.
If
u,
v E Cb(n), then
(LDu, v) =
-l
vAu
= {
\7u·
\7v - {
vaau
(Green's first identity)
in
ian
n
= l
\7u·
\7v (since v = 0 on
an)
= { u
a
OV
- {
uAv
(Green's first identity)
ian
n
in
= -
In
uAv
(since v = 0 on
an)
= (U,LDV),
It
is
no more difficult to prove the symmetry of
-A
under Neumann conditions
(see Exercise 6).
Exercises
1.
How
does the heat equation (8.3) change if
p,
c,
and
K,
are functions of
x?
