Gockenbach M.S. Partial Differential Equations. Analytical and Numerical Methods
Подождите немного. Документ загружается.


348
Chapter
8.
Problems
in
multiple spatial dimensions
Putting together
the PDE and the
initial conditions,
we
obtain
the
following
sequence
of
IVPs:
m,
n
—
1,2,3,
—
The
solutions
are
where
8.2.4
Other
boundary
conditions
for the
rectangle
Using
separation
of
variables,
it is
straightforward
to find the
eigenvalues
and
eigen-
functions
for the
negative Laplacian,
on a
rectangle, under Neumann conditions
or
some
combination
of
Dirichlet
and
Neumann conditions.
For
example,
if
£)
is the
rectangle (8.10)
and
dtl
=
TI
U
T
2
U
T
3
U
T
4
,
with
the
F;
defined
as in
(8.13),
we
can
consider
the
following
IBVP:
By
applying
the
method
of
separation
of
variables,
we can
determine
the
appropriate Fourier series
to
represent
the
solution:
(see
Exercise 14).
The
determination
of the
coefficients
a
mn
(t)
follows
the
now-
familiar
pattern.
348
Chapter
8.
Problems
in
multiple spatial dimensions
Putting together the
PDE
and the initial conditions,
we
obtain the following
sequence
of
IVPs:
m, n =
1,2,3,.
...
The solutions
are
amn(t) = d
mn
sin (CVm2 + n
2
7ft)
, m, n =
1,2,3,
...
,
where
We graph selected snapshots
of
u in Figure 8.6.
8.2.4 Other boundary conditions for the rectangle
Using separation of variables,
it
is straightforward
to
find
the
eigenvalues and eigen-
functions for
the
negative Laplacian, on a rectangle, under Neumann conditions or
some combination of Dirichlet and Neumann conditions. For example, if
n
is
the
rectangle (8.10) and
an
= r
1
U r
2
U
r3
U r
4
, with the r
i
defined as in (8.13),
we
can consider
the
following IBVP:
au
pc
at
-
K,Llu
=
f(x,
t), x E
n,
t>
0,
u(x,O) =
'I/J(x),
x E
n,
u(x,
t) = 0, x E
rl,
t>
0,
au
an
(x,
t)
= 0, x E r
2
,
t >
0,
(8.21 )
au
an
(x,
t)
= 0, x E r
3
,
t > 0,
u(x,t)
=0,
xEr
4
,
t>O.
By applying the method of separation of variables,
we
can determine the
appropriate Fourier series to represent
the
solution:
(see Exercise 14). The determination of
the
coefficients amn(t) follows
the
now-
familiar pattern.

Figure
8.6. Snapshots
of the
vibrating membrane
of
Example
8.4'-
t =
5 •
1CT
4
(upper
left),
t =
1(T
3
(upper
right),
t = 2 •
1(T
3
(lower
left),
t = 3 •
1(T
3
(lower
right).
8.2.5 Neumann boundary conditions
Neumann conditions
are
slightly more
difficult
to
handle
than
Dirichlet
or
mixed
boundary conditions. This
is
simply because Neumann conditions lead
to two
dif-
ferent
kinds
of
eigenfunctions,
the
constant function
1, and the
cosines
of
increasing
frequencies.
To be
specific,
the
reader
will
recall
from
Section
6.2
that
the
eigenpairs
of
the
negative second derivative operator, under Neumann conditions,
are
8.2. Fourier
series
on a
rectangular domain
349
Just
as in the
case
of
Dirichlet
or
mixed boundary conditions,
the
eigenfunctions
of
the
negative Laplacian, under Neumann conditions
and on the
rectangle,
are
products
of the
one-dimensional eigenfunctions. Since there
are two
formulas
for
the
one-dimensional eigenfunctions, this leads
to
four
different
formulas
for the
8.2. Fourier
series
on
a rectangular domain
349
X 10-
4
X 10
-4
2
0
0
- 2
- 1
1 1
1
0
0
0
0
X 10
-4
X 10
-4
1 2
0
0
- 1
- 2
1
1
1
1
0
0
0
0
Figure
8.6.
Snapshots
of
the vibrating membrane
of
Example 8.4: t =
5 .
10-
4
(upper left), t =
10-
3
(upper right), t =
2·
10-
3
(lower left), t =
3·
10-
3
(lower right).
8.2.5
Neumann boundary conditions
Neumann conditions are slightly more difficult
to
handle
than
Dirichlet
or
mixed
boundary
conditions. This is simply because Neumann conditions lead
to
two dif-
ferent kinds
of
eigenfunctions,
the
constant function 1,
and
the
cosines of increasing
frequencies. To be specific,
the
reader will recall from Section 6.2
that
the
eigenpairs
of
the
negative second derivative operator, under Neumann conditions, are
Ao
= 0, ro(x) = 1,
n
2
7r
2
(n7rx)
An
=
T'
rn(X) = cos -e- , n =
1,2,3,
....
Just
as in
the
case of Dirichlet or mixed
boundary
conditions,
the
eigenfunctions
of
the
negative Laplacian, under Neumann conditions
and
on
the
rectangle, are
products of
the
one-dimensional eigenfunctions. Since
there
are two formulas for
the
one-dimensional eigenfunctions, this leads
to
four different formulas for
the

Chapter
8.
Problems
in
multiple spatial dimensions
two-dimensional
eigenfunctions
(see
Exercise
12):
By
the
same reasoning given
in
Section 8.2.1, this collection
of
eigenfunction
should
be
sufficient
to
represent
any
function
in
(7(fi);
the
series representation
is
where
350
A
steady-state
Neumann problem imposes
a
compatibility condition
on the
right-hand side
of the
PDE,
as
might
be
expected
from
the
existence
of a
zero
picrpnva.liip
Snnnnsp
11.
is
a.
solution
nf
t.hp
RVP
The
compatibility condition
follows
from
the
divergence theorem:
If
/
satisfies
the
compatibility condition
350
Chapter
8. Problems
in
multiple spatial dimensions
two-dimensional eigenfunctions (see Exercise 12):
Aoo
= 0,
')'oo(x)
=
1,
(8.22)
By
the
same reasoning given in Section 8.2.1, this collection of eigenfunction should
be sufficient
to
represent any function in C(IT)j the series representation is
m7rXl
n7rX2
0000
()
( )
+
fl~amnCOS
l;-
cos T '
where
aoo
=
£:£21
11
112
f(Xl,X2)
dX2
dx1,
amo
=
£~2
foil
fol2
f(Xl,
X2)
cos
(m~Xl
)
dX2
dx
1
,
aO
n
=
£1
2
£2
foil
fol2
f(Xl,
X2)
cos
(n;:2
)
dX2
dXl,
a
mn
=
£1~2
foil
fol2
f(Xl,
X2)
cos
(m~Xl
) cos
(n;:2
)
dX2
dXl.
A steady-state Neumann problem imposes a compatibility condition on
the
right-hand side of the PDE, as might be expected from
the
existence of a zero
eigenvalue. Suppose
u
is
a solution of
the
BVP
-.:lu
=
f(x)
in
n,
au
an
= 0 on
an.
The
compatibility condition follows from
the
divergence theorem:
f f = - f .:lu = - f
V'
. V'u = - f V'u. n = _ f au =
o.
J
o
Jo Jo
J
ao
Jao
an
If
f satisfies
the
compatibility condition
If=O,
(8.23)
8.2. Fourier series
on a
rectangular
domain
351
then
the
Neumann problem (8.23)
has
infinitely many solutions, while
if /
does
not
satisfy
the
compatibility condition, then there
is no
solution.
Example
8.5.
We
will
solve
the
Neumann problem
where
fi
is the
unit
square.
We
write
the
solution
as
Then
We
also
have
where
The
reader
should
notice that
CQO
= 0 is the
compatibility
condition,
and so
there
are
infinitely
many solutions. Equating
the
series
for
—Aw
and f
yields
8.2. Fourier
series
on
a rectangular domain
351
then
the
Neumann
problem (8.23) has infinitely
many
solutions, while if f does
not
satisfy
the
compatibility condition,
then
there
is no solution.
Example
8.5.
We will solve the Neumann problem
2 1
-~U=XIX2-6
inn,
au
an
= 0 on
an,
where n is the
unit
square.
We
write the solution
as
00 00
U(Xl'
X2)
=
aOO
+ L
amo
cos
(m1rxt)
+ L
aO
n
cos (
n1rX
2)
m=l
n=l
00 00
+ L L a
mn
cos
(m1rxd
cos (
n1rX
2).
m=l
n=l
Then
00 00
-~U(Xl'
X2)
= L m
2
1r
2
a
m
O
cos
(m1rxt)
+ L
n21r2aOn
cos (
n1rX
2)
m=l
n=l
00
00
+ L
2:=
(m
2
1r2
+ n
2
1r2)
a
mn
cos
(m1rxd
cos (
n1rX
2).
m=l
n=l
We
also
have
00 00
f(Xl,
X2)
=
Coo
+ L
Cmo
cos (
m1rX
l)
+
2:=
COn
cos (
n1rX
2)
m=l
n=l
00
00
+ L L C
mn
cos
(m1rxd
cos (
n1rX
2)
,
m=ln=l
where
COO
= 0,
2(-1)m
Cmo=
22'
m1r
2((-1)n-1)
COn
= 3 2 2 '
n1r
8 ((
-1)
m+n + (
-1)
m+1
)
C
mn
= 2 2 4 .
mn1r
(8.24)
The reader should notice that
COO
= 0 is the compatibility condition, and
so
there
are
infinitely many solutions. Equating the series for
-~U
and f yields
CmO
amo
= ----:!2'
m1r
Con
aO
n
=
22'
n1r

352
Chapter
8.
Problems
in
multiple spatial dimensions
with
ttQQ
undetermined.
The
graph
of
u,
with
aoo
=
0,
is
shown
in
Figure
8.7.
Figure
8.7.
The
solution
to the
BVP
in
Example 8.5.
This
graph
was
produced
using
a
total
of 120
terms
of the
(double)
Fourier cosine series.
8.2.6 Dirichlet
and
Neumann problems
for
Laplace's
equation
The PDE
is
called Laplace's equation.
This
equation, with inhomogeneous boundary condi-
tions,
is
commonly
encountered
in
applications.
For
example,
a
steady-state
heat
flow
problem with
no
heat
source,
in a
homogeneous domain, leads
to
Laplace's
equation, which
can be
paired with inhomogeneous Dirichlet
or
Neumann con-
ditions.
The
Dirichlet conditions indicate
that
the
temperature
is fixed on the
boundary, while
the
Neumann conditions indicate
that
the
heat
flux is
prescribed.
As
another example,
if a
membrane
is
stretched
on a
frame
described
by a
curve
(x,y,g(xi,X2)),
(xi,x<z)
€
Oft,
and if no
transverse
force
is
applied, then
the
shape
of the
membrane
is
described
by the
solution
of
Laplace's equation with
inhomogeneous Dirichlet conditions
u(xi,#2)
=
#(#15
#2),
(^1,^2)
G
d^l.
We
will consider
the
following
Dirichlet problem
for
Laplace's equation:
If
we
wish
to
solve (8.26) using
the
method
of
Fourier series, then
it is
desirable
to
shift
the
data
to
obtain homogeneous boundary conditions.
The
reader should
352
Chapter
8.
Problems
in
multiple spatial dimensions
with
aoo
undetermined. The
graph
of
u, with
aoo
= 0, is shown in Figure 8.7.
0.06
0.04
0.02
o
- 0.02
-0.
04
1
o 0
Figure
8.7. The solution
to
the
BVP
in Example 8.5. This
graph
was
produced using a total
of
120 terms
of
the (double) Fourier cosine series.
8.2.6 Dirichlet
and
Neumann
problems
for
Laplace's equation
The
PDE
-~U
= ° in n
(8.25)
is
called Laplace's equation. This equation, with inhomogeneous boundary condi-
tions, is commonly encountered in applications. For example, a steady-state heat
flow
problem with no heat source, in a homogeneous domain, leads
to
Laplace's
equation, which can be paired with inhomogeneous Dirichlet or Neumann con-
ditions.
The
Dirichlet conditions indicate
that
the temperature
is
fixed on the
boundary, while the Neumann conditions indicate
that
the
heat flux is prescribed.
As
another example, if a membrane
is
stretched on a frame described by a
curve
(x,y,g(Xl,X2)), (Xl,X2) E
an,
and if no transverse force
is
applied, then
the
shape of the membrane
is
described by the solution of Laplace's equation with
inhomogeneous Dirichlet conditions
U(Xl,X2) = g(Xl,X2), (Xl,X2) E
an.
We
will consider
the
following Dirichlet problem for Laplace's equation:
-~U
= ° in
n,
(8.26)
U = 9 on
an.
If
we
wish
to
solve (8.26) using
the
method of Fourier series, then
it
is desirable
to shift
the
data
to
obtain homogeneous boundary conditions.
The
reader should

8.2. Fourier
series
on a
rectangular domain
353
recall
the
method
of
shifting
the
data
from
Section 5.3: Given
a
smooth function
p
defined
on ft
satisfying
p(xi,#2)
=
5(^1,^2)
on
5ft,
we
define
v = u
—
p,
where
u
satisfies
(8.26). Then,
in ft,
and,
on
5ft,
Therefore,
v
satisfies
the BVP
For a
general domain
ft, it may be
difficult
or
impossible
to find
(explicitly)
a
smooth
function
p,
defined
on all of ft and
satisfying
p(x\,x<2)
=
g(xi,xz]
for all
(rci,
#2)
€
5ft.
However,
for
such
a
general domain,
it is
probably impossible
to find
the
eigenvalues
and
eigenfunction
of the
negative
Laplacian,
also.
For the
simple
domains (rectangles
and
disks)
for
which
we can
explicitly
find the
eigenpairs
of the
Laplacian,
we can
also
find the
function
p
explicitly.
For the
rectangle (8.10),
the
boundary
data
g
will
typically
be
described
as
follows:
where
9ft
is
partitioned
as in
(8.13).
There
is a
completely mechanical technique
for
finding
p
:
ft
—>
R
satisfying
P(XI,XZ)
=
g(xi,#2)
on
5ft;
however, this technique
requires
a
lengthy explanation, which
we
relegate
to
Appendix
B. In the
following
example,
we use the
results
from
that
Appendix, which interested reader
can
consult
for
the
details.
Example
8.6.
We
assume that
an
elastic membrane
of
dimensions
10 cm by 15 cm
occupies
the set
Then
u
satisfies
and the
edges
of the
membrane
are fixed to a
frame,
so
that
the
vertical
deflection
of
the
membrane
satisfies
the
following
boundary
conditions:
8.2. Fourier
series
on
a rectangular domain
353
recall
the
method of shifting the
data
from Section 5.3: Given a smooth function p
defined on n satisfying P(X1,X2) = g(X1,X2) on
an,
we
define v = u - p, where u
satisfies (8.26). Then, in
n,
-Llv
=
-Llu
+ Llp = 0 + Llp = Llp,
and, on
an,
v = u - p = g - g =
O.
Therefore, v satisfies
the
BVP
-Llv
= Llp in
n,
v = 0 on
an.
(8.27)
For a general domain
n,
it
may be difficult or impossible to find (explicitly)
a smooth function
p, defined on all of n and satisfying
P(X1'
X2)
= g(X1'
X2)
for all
(Xl,
X2)
E
an.
However, for such a general domain,
it
is
probably impossible
to
find
the
eigenvalues and eigenfunction of the negative Laplacian, also. For
the
simple
domains (rectangles and disks) for which
we
can explicitly find
the
eigenpairs of the
Laplacian,
we
can also find
the
function p explicitly.
For the rectangle (8.10), the boundary
data
g will typically be described as
follows:
(X1,X2) E r
1
,
(X1,X2)
E r
2
,
(X1,X2)
E r
3
,
(X1,X2) E r
4
,
where
an
is
partitioned as in (8.13). There
is
a completely mechanical technique for
finding
p:
n
-+
R satisfying P(X1,X2) = g(X1,X2) on
an;
however, this technique
requires a lengthy explanation, which
we
relegate to Appendix B. In the following
example,
we
use
the
results from
that
Appendix, which interested reader can consult
for
the
details.
Example
8.6.
We assume
that
an elastic membrane
of
dimensions
10
cm by
15
cm
occupies the
set
n =
{x
E
R2
: 0 <
Xl
< 10, 0 <
X2
<
15},
and
the edges
of
the membrane are fixed to a frame, so that the vertical deflection
of
the membrane satisfies the following boundary conditions:
Then
u satisfies
~
200'
1
X2
2"
-
30'
Jc.
_
~
10
100'
~
15
'
-Llu
= 0
in
n,
u = g on
an.
(X1,X2) E r
1
,
(X1,X2) E r
2
,
(X1,X2) E r
3
,
(Xl,
X2)
E r
4
·
(8.28)

The
desired
solution
u
is
then given
by
The
Neumann problem
for
Laplace's equation
can be
handled
in
much
the
same way.
An
example
is
given
in
Appendix
B
(Example
B.2).
8.2.7
Fourier
series
methods
for a
rectangular
box in
three
dimensions
It is
straightforward,
in
principle,
to
extend
the
Fourier series method
to
problems
posed
on a
rectangular
box in
three
dimensions.
For
example,
if
354
Chapter
8.
Problems
in
multiple
spatial dimensions
A
smooth function
p
satisfying
p = g on
d£t
is
and
we
have
We
therefore
solve
where
/(xi,^)
=
(#2
—
15)/1500,
by the
Fourier series method.
The
eigenpairs
of
—A
on fi are
The
Fourier
coefficients
of f are
and
so the
solution
v is
given
by
where
The
graph
of
u is
shown
in
Figure
8.8.
354 Chapter
8.
Problems
in
multiple spatial dimensions
A
smooth
function
p satisfying p = g
on
an
is
(
)
_ 20X2 -
2X1X2
- Xi(X2 -
15)
P X1,X2 - 3000 '
and
we have
We
therefore solve
-b.v
=
f(x1,x2)
in
0.,
v = 0
on
an,
where
f(x1,x2)
=
(X2
-15)/1500,
by the Fourier series method. The eigenpairs
of
-b.
on
0.
are
m
2
'Jr2
n
2
'Jr2
(m'Jrx)
(n'Jrx)
Amn =
100
+
225
' '¢mn(X1,X2) = sin
~
sin
Ts
'
m,n
=
1,2,3,
....
The Fourier coefficients
of
fare
C
mn
=
1:0
fo10 fo15
f(x1,x2)
sin
(m;;l)
sin
(n~:2)
dX2dxI
(-I)m-l
= 2 '
m,n
=
1,2,3,
...
,
25mn'Jr
and
so the solution v is given by
where
C
mn
a
mn
=
~,
m,n
=
1,2,3,
....
"mn
The
desired solution u is
then
given
by
The graph
of
u is shown
in
Figure
B.B.
The Neumann problem for Laplace's equation can be handled in much the
same
way.
An example
is
given in Appendix B (Example B.2).
8.2.7 Fourier
series
methods for a rectangular
box
in
three
dimensions
It
is
straightforward, in principle,
to
extend the Fourier series method to problems
posed on a rectangular box in three dimensions. For example, if
0.
= {(Xl,
X2,
X3)
E R
3
:
0 <
Xl
< £ I, 0 <
X2
<
£2,
0 <
X3
<
£3}
,
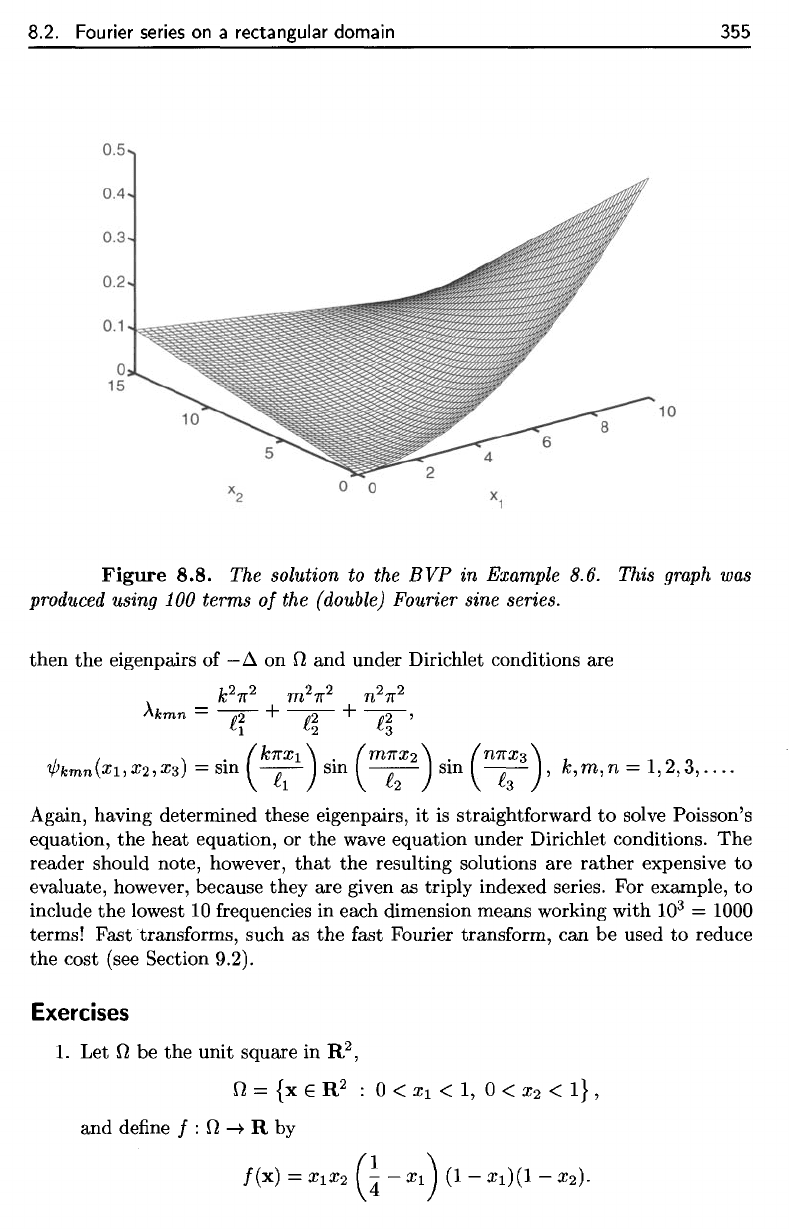
8.2. Fourier
series
on a
rectangular domain
355
Figure
8.8.
The
solution
to the BVP in
Example 8.6.
This
graph
was
produced
using
100
terms
of the
(double)
Fourier sine series.
then
the
eigenpairs
of
—A
on
f)
and
under Dirichlet conditions
are
Again,
having determined these eigenpairs,
it is
straightforward
to
solve
Poisson's
equation,
the
heat
equation,
or the
wave equation under Dirichlet conditions.
The
reader should note, however,
that
the
resulting solutions
are
rather
expensive
to
evaluate, however, because they
are
given
as
triply indexed series.
For
example,
to
include
the
lowest
10
frequencies
in
each dimension means working with
10
3
=
1000
terms!
Fast
transforms, such
as the
fast Fourier transform,
can be
used
to
reduce
the
cost (see Section 9.2).
Exercises
1.
Let
fJ
be the
unit square
in
R
2
,
and
define
/ :
fi
—>
R by
8.2. Fourier
series
on
a rectangular domain
0.5
0.4
0.3
0.2
0.1
o
15
o 0
355
10
Figure
8.8.
The solution to the
BVP
in Example 8.6. This graph was
produced using 100
terms
of
the (double) Fourier sine series.
then
the
eigenpairs of
-b.
on n and under Dirichlet conditions are
k2~2
m2~2
n2~2
Akmn
= T +
----er
+
T'
1/Jkmn
(Xl,
X2,
X3)
= sin
(k~~l
) sin ( m;2
X2
) sin
(n~:3
) ,
k,m,n
=
1,2,3,
....
Again, having determined these eigenpairs, it
is
straightforward
to
solve Poisson's
equation,
the
heat equation, or
the
wave equation under Dirichlet conditions.
The
reader should note, however,
that
the
resulting solutions are
rather
expensive
to
evaluate, however, because they are given as triply indexed series. For example,
to
include
the
lowest 10 frequencies in each dimension means working with
10
3
= 1000
terms! Fast transforms, such as
the
fast Fourier transform, can be used
to
reduce
the
cost (see Section 9.2).
Exercises
1. Let n be
the
unit square in R2,
n =
{x
E R2 0 <
Xl
< 1, 0 <
X2
<
1}
,
and
define f : n
~
R by
f(x)
=
XIX2
(~
- Xl)
(1
-
xd(l
-
X2)'

356
Chapter
8.
Problems
in
multiple
spatial
dimensions
(a)
Compute
the
(double) Fourier sine series
of
/
(that
is,
compute
the
coefficients
c
mn
).
(b)
Graph
the
error
in
approximating
/ by
for
M
= N = 2 and
again
for M = N = 5.
2.
Repeat
the
previous exercise with
3.
Solve
the BVP
where
fJ
is the
unit square
in R
2
and / is the
function
in
Exercise
1.
4.
Solve
the BVP
where
£)
is the
unit square
in
R
2
and / is the
function
in
Exercise
2.
5.
Suppose
that
a
square iron plate
of
side length
50cm
initially
has
constant
temperature
of 5
degrees Celsius
and its
edges
are
placed
in an ice
bath
(0
degrees
Celsius) (the plate
is
perfectly
insulated
on the top and
bottom).
At
the
same time
that
the
edges
are
placed
in the ice
bath,
we
begin adding
heat energy everywhere
in the
interior
of the
plate
at the
(constant)
rate
of
0.02W/cm
3
.
The
material constants
for
iron
are p =
7.88
g/cm
3
,
c =
0.437
J/(gK),
and
«
=
0.836W/(cmK).
(a)
Formulate
an
IBVP
that
describes
the
temperature
u(x,£).
(b)
Find
the
(double) Fourier sine series
of
u.
(c)
Find
the
Fourier series
of the
steady-state temperature
u
a
.
What
BVP
does
u
s
satisfy?
(d)
How
close
is u to
u
s
after
10
minutes? Graph
the
difference
in the two
temperature distributions.
356
Chapter
8. Problems
in
multiple spatial dimensions
(a) Compute
the
(double) Fourier sine series
00
00
L L C
mn
sin (m1TxI) sin (
n1Tx
2)
m=ln=l
of f
(that
is, compute
the
coefficients c
mn
).
(b)
Graph
the
error in approximating f by
M N
L L C
mn
sin (
m1Tx
l)
sin (
n1Tx
2)
m=l
n=l
for M = N = 2
and
again for M = N =
5.
2.
Repeat
the
previous exercise with
3. Solve
the
BVP
-Llu
=
f(x)
in
n,
u = 0
on
an,
where n
is
the
unit
square in R2
and
f is
the
function in Exercise
1.
4. Solve
the
BVP
-Llu
=
f(x)
in
n,
u
=0
on
an,
where n is
the
unit
square in R
2
and
f is
the
function in Exercise
2.
5.
Suppose
that
a square iron
plate
of
side length 50 cm initially has constant
temperature
of
5 degrees Celsius
and
its
edges are placed in
an
ice
bath
(0
degrees Celsius) (the plate is perfectly insulated
on
the
top
and
bottom). At
the
same time
that
the
edges are placed
in
the
ice
bath,
we begin adding
heat
energy everywhere in
the
interior of
the
plate
at
the
(constant)
rate
of
0.02W/cm
3
•
The
material constants for iron are p =
7.88g/cm
3
, C
=
0.437
J/(gK),
and".
= 0.836
W/(cm
K).
(a) Formulate
an
IBVP
that
describes
the
temperature
u(x,
t).
(b)
Find
the
(double) Fourier sine series of u.
(c)
Find
the
Fourier series
of
the
steady-state
temperature
us.
What
BVP
does
Us
satisfy?
(d) How close is u
to
Us
after 10 minutes?
Graph
the
difference
in
the
two
temperature
distributions.

where
8.2.
Fourier
series
on a
rectangular
domain
357
6. Let u €
C(fJ)
be
given,
and
define
FMN
to be the
subspace
of
C(f))
spanned
by
where
Show
that
the
best approximation
to
u
(in the
I/
2
norm)
from
FMN
is
given
by
(8.17), (8.18).
7.
Consider
the
iron plate
of
Exercise
5.
Suppose
that
plate initially
has
constant
temperature
2
degrees Celsius
and
that
at
time
t = 0 the
edges
are
instantly
brought
to
temperature
5
degrees
and
held there.
How
long does
is
take until
the
entire plate
has
temperature
at
least
4
degrees? (Hint:
To
deal with
the
inhomogeneous boundary condition,
just
shift
the
data.
It is
trivial
in
this
case, because
the
boundary
data
is
constant.)
8.
Suppose
fi
is the
rectangle
and
that
u is a
twice-continuously
differentiate
function
defined
on
fL
Let
the
Fourier sine series
of u be
Suppose
u
satisfies
u(x)
= 0 for x
e
dfl.
Prove
that
the
Fourier series
of
—Aw
is
9.
In
Example 8.4,
how
long does
it
take
for the
leading edge
of the
wave
to
reach
the
boundary
of
0?
Is the
computed time consistent with Figure 8.6?
10.
Suppose
£)
is a
domain
in R
2
or R
3
with
a
piecewise smooth boundary
dft,
and
suppose
Oft
is
partitioned into
2
disjoint subsets:
dti,
=
FI
U
F2-
Define
Let
L
m
:
C^(fl)
—>•
C(fi)
be
defined
by
L
m
u
=
—Aw.
Show
that
L
m
is
symmetric
and has
only positive eigenvalues.
8.2. Fourier
series
on
a rectangular domain
357
6.
Let u E C(f1) be given,
and
define FMN
to
be
the
subspace of C(f1) spanned
by
{~mn
: m =
1,2,
...
,
M,
n =
1,2,
...
,
N},
where
~mn(Xl'
X2)
= sin
(m~Xl
) sin
(n;:2
).
Show
that
the
best approximation
to
u (in
the
L2 norm) from FMN is given
by (8.17), (8.18).
7. Consider
the
iron plate of Exercise
5.
Suppose
that
plate initially has constant
temperature
2 degrees Celsius
and
that
at
time t = 0
the
edges are instantly
brought
to
temperature
5 degrees and held there. How long does
is
take until
the
entire plate has
temperature
at
least 4 degrees? (Hint: To deal with
the
inhomogeneous boundary condition,
just
shift
the
data.
It
is trivial in this
case, because the boundary
data
is constant.)
8. Suppose n is
the
rectangle
and
that
u is a twice-continuously differentiable function defined on
n.
Let
the
Fourier sine series of u be
Suppose
u satisfies
u(x)
= 0 for x E
an.
Prove
that
the
Fourier series of
-.6.u
is
where
9.
In Example 8.4, how long does
it
take for
the
leading edge of
the
wave
to
reach
the
boundary of
n?
Is
the
computed time consistent with Figure 8.6?
10. Suppose n is a domain in
R2 or R3 with a piecewise smooth boundary
an,
and suppose
an
is partitioned into 2 disjoint subsets:
an
= r
1
U r
2
.
Define
Let
Lm
:
C!(f1)
-t
C(f1) be defined by
Lmu
=
-.6.u.
Show
that
Lm
is
symmetric
and
has only positive eigenvalues.
