Gockenbach M.S. Partial Differential Equations. Analytical and Numerical Methods

49

The

reader

is

assumed

to

have

read

Section

4.6

and/or

Section 5.7;

the

material

on the

Dirac

delta

function

found

in

those

two

sections

is

prerequisite

for

this

section.

318

Chapter

7.

Waves

(b)

Apply

the

Galerkin method

to

obtain

a

system

of

ODEs with initial

conditions.

How do the

mass

and

stiffness

matrices change

from

the

case

of

a

homogeneous bar?

8.

Repeat Exercise

6,

assuming

now

that

the bar is

heterogeneous with density

and

stiffness

(The coordinate

x is

measured

in

meters:

0 < x < 1.)

7.4

Point

sources

and

resonance

We

now

consider

two

special experiments

that

can

lead

to

resonance:

• A

metal string (such

as a

guitar string), with both ends

fixed, is

subjected

to an

oscillatory electromagnetic

force

generated

by a

small electromagnet.

When

the

frequency

of the

external

force

equals

one of the

natural frequencies

of

the

string, resonance occurs.

• A

string

has one end fixed, and the

other

is

mechanically moved

up and

down:

u(i,t)

=

sin(27ru;£).

Again, resonance occurs when

the

applied

frequency,

w,

equals

one of the

natural frequencies

of the

string.

In

the first

experiment,

the

modeling involves

the

Dirac delta

function.

49

7.4.1

The

wave

equation

with

a

point

source

We

begin with

the

following

IBVP

for the

wave equation:

where

we

assume

that

0 < a < t.

This models

the

vibrating string, where

the

string

is

assumed

to

vibrate

due to a

time-varying

force

applied

at the

point

x = a.

We

can

solve

(7.26)

exactly

as in

Section 7.2.

We use the

sifting

property

of

the

delta

function

to

compute

the

Fourier sine

coefficients

of

f(t}8(x

—

a):

318 Chapter 7. Waves

(b) Apply

the

Galerkin

method

to

obtain a system of ODEs with initial

conditions. How do

the

mass

and

stiffness matrices change from

the

case

of a homogeneous bar?

8. Repeat Exercise 6, assuming now

that

the

bar

is heterogeneous with density

p(x) = 7500 +

1000x

kg/m

3

and

stiffness

k(x) =

1.9.10

11

+ 10

1O

xN/m

2

•

(The coordinate x is measured in meters: 0 < x < 1.)

7.4 Point

sources

and resonance

We now consider two special experiments

that

can lead

to

resonance:

• A metal string (such as a

guitar

string), with

both

ends fixed, is subjected

to

an

oscillatory electromagnetic force generated by a small electromagnet.

When

the

frequency of the external force equals one of

the

natural

frequencies

of

the

string, resonance occurs .

• A string has one end fixed,

and

the

other is mechanically moved up

and

down:

u(l,

t) = sin

(21fwt).

Again, resonance occurs when

the

applied frequency,

w,

equals one of

the

natural

frequencies of

the

string.

In

the

first experiment,

the

modeling involves the Dirac delta function.

49

7.4.1 The

wave

equation with a point

source

We begin with

the

following IBVP for

the

wave equation:

fpu

2fPu

at

2

-

c

ax

2

= f(t)8(x - a), ° < x <

£,

t > to,

u(x,

to)

= 0, 0 < x <

£,

ou

at

(x,

to)

= 0, 0 < x <

£,

u(O,t) = 0, t >

to,

u(£, t) = 0, t >

to,

(7.26)

where

we

assume

that

0 < a <

£.

This models

the

vibrating string, where

the

string

is assumed

to

vibrate due

to

a time-varying force applied

at

the

point x =

a.

We

can solve (7.26) exactly as in Section 7.2.

We

use

the

sifting property of

the

delta function

to

compute

the

Fourier sine coefficients

of

f(t)8(x -

a):

cn(t) =

~

1£

f(t)8(x -

a)

sin

(n;x)

dx

49The

reader

is assumed

to

have

read

Section 4.6

and/or

Section 5.7;

the

material

on

the

Dirac

delta

function found in those two sections is prerequisite for this section.

7.4.

Point

sources

and

resonance

319

We

then must solve

the

following

IVP

to find the

unknown

coefficients

a

n

(t):

According

to the

results derived

in

Section

4.2.2,

the

solution

to

this

IVP is

Oscillatory forcing

and

resonance

We

are

interested

in the

case

in

which

f(t)

is

oscillatory.

For

convenience,

we

take

I

— 1 and

to

— 0, and let

/(t)

= sin

(2,-jrut).

Then

the

solution

to the

IBVP

is

where

A

lengthy

but

elementary calculation shows

that,

if

u;

/

cn/2,

then

One

the

other hand,

if

cj

=

cm/2,

one of the

natural

frequencies

of the

string, then

(formula

(7.27)

still holds, with

o>

=

cm/2,

for the

coefficients

a

n

(t)

with

n

/

m).

In

the

case

that

the

external

frequency

a;

is a

natural

frequency

of the

string,

the

result (7.28) shows

that

the

string oscillates with

an

ever-increasing ampli-

tude. (The reader should notice

the

factor

of

t,

which

shows

that

the

amplitude

increases without bound.) This phenomenon

is

called resonance. When

the

exter-

nal

frequency

is

close

to but not

equal

to a

natural

frequency,

formula

(7.27)

shows

that

the

nearby

natural

frequency

is

amplified

in the

solution (though

it

remains

bounded)—this

is

because

the

denominator

in

(7.27)

is

very small.

7.4. Point sources

and

resonance

319

-

2f(t)

1£

!i:(

).

(n1fX) d

---

ux-a

SIn

- x

e 0 e

= 2 sin

~T)

f(t).

We

then must solve the following IVP

to

find the unknown coefficients an(t):

According

to

the

results derived in Section 4.2.2, the solution

to

this IVP

is

2 sin

(n1ra)

it

(c:n1f

)

an(t)

= £ sin

-----n(t

-

s)

f(s)

ds.

c:n1f

to

~

Oscillatory forcing and resonance

We

are interested in the case in which

f(t)

is

oscillatory. For convenience,

we

take

e = 1 and

to

= 0, and let

f(t)

= sin

(21fwt).

Then

the

solution to the IBVP

is

00

u(x, t) = L an(t) sin (mfx),

n=I

where

an(t) = 2 sin (mfa)

rt

sin

(21fws)

sin (cn1f(t - s))

ds.

c:n1f

10

A lengthy

but

elementary calculation shows

that,

if w

=I

c:n/2, then

( )

2 sin

(n1fa)

(c:n

sin

(21fwt)

- w sin

(c:n1ft))

an

t = .

cn1f2(c

2

n

2

-

4w

2

)

(7.27)

One the other hand,

if

w = c:m/2, one of the natural frequencies of the string, then

()

_ sin

(m1fa)

(sin

(c:m1ft)

-c:m1ftcos(c:m1ft))

amt-

222

cm1f

(7.28)

(formula (7.27) still holds, with

w =

c:m/2,

for

the

coefficients an(t) with n

=I

m).

In

the

case

that

the external frequency w is a natural frequency of

the

string,

the result (7.28) shows

that

the string oscillates with an ever-increasing ampli-

tude. (The reader should notice

the

factor of t, which shows

that

the amplitude

increases without bound.) This phenomenon

is

called resonance. When

the

exter-

nal frequency is close to

but

not equal

to

a natural frequency, formula (7.27) shows

that

the nearby natural frequency

is

amplified in the solution (though

it

remains

bounded)-this

is

because

the

denominator in (7.27)

is

very small.

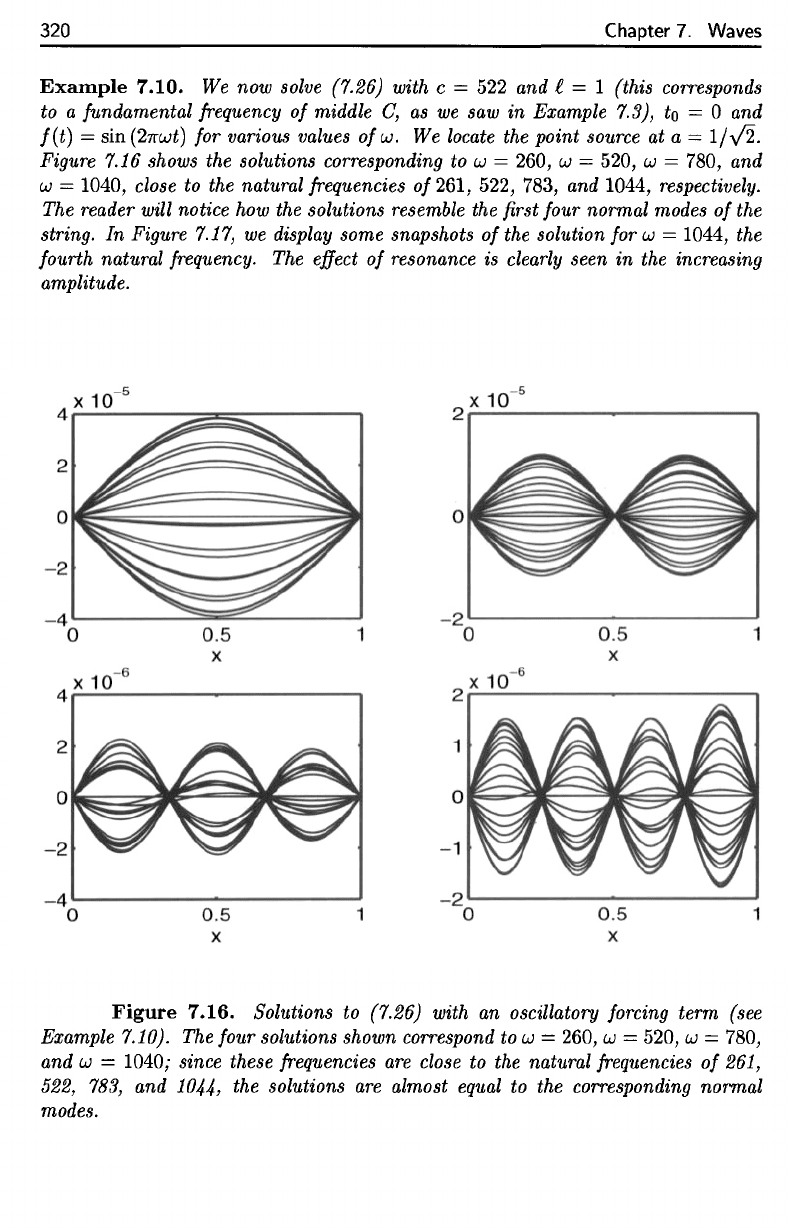
320

Chapter

7.

Waves

Example

7.10.

We now

solve (7.26) with

c = 522 and

1

=

1

(this corresponds

to a

fundamental frequency

of

middle

C, as we saw in

Example

7.3),

to

= 0 and

f(t)

=

s'm(27rujt)

for

various values

ofui.

We

locate

the

point

source

at a =

l/\/2-

Figure

7.16

shows

the

solutions corresponding

to

u

=

260,

LJ

=

520,

u;

=

780,

and

u}

=

1040,

close

to the

natural frequencies

0/261,

522,

783,

and

1044,

respectively.

The

reader will notice

how the

solutions resemble

the first

four normal modes

of

the

string.

In

Figure

7.17,

we

display

some snapshots

of

the

solution

for u =

1044,

the

fourth natural frequency.

The

effect

of

resonance

is

clearly

seen

in the

increasing

amplitude.

Figure 7.16.

Solutions

to

(7.26) with

an

oscillatory forcing

term

(see

Example 7.10).

The

four solutions shown correspond

touj

=

260,

w

=

520,

u;

=

780,

and

uj

=

1040;

since these frequencies

are

close

to the

natural frequencies

of

261,

522,

783,

and

1044)

the

solutions

are

almost

equal

to the

corresponding normal

modes.

320

Chapter 7. Waves

Example

7.10. We now solve (7.26) with c = 522 and l = 1 (this corresponds

to a fundamental frequency

of

middle

C,

as

we

saw

in

Example 7.3),

to

= 0 and

f(t)

= sin

(27rwt)

for various values

of

w.

We locate the point source at a =

1/0.

Figure 7.16 shows the solutions corresponding to w = 260, w = 520, w = 780, and

w = 1040, close to the natural frequencies

of

261, 522, 783, and 1044, respectively.

The reader will notice how the solutions resemble the first four normal modes

of

the

string.

In

Figure 7.17,

we

display some snapshots

of

the solution for w = 1044, the

fourth natural frequency. The effect

of

resonance is clearly seen

in

the increasing

amplitude.

4 X

10

-

5

2

0

- 2

- 4

0

0.5

1

x

4 X

10

-

6

- 4

~--------------------~

o

0

.5

x

1

-

2~------------------~

o 0.5

x

1

10

-

6

2~

x

~~

__________________

~

1

- 1

-

2~----

----------------~

o

0

.5

x

Figure

7.16. Solutions to (7.26) with an oscillatory forcing term (see

Example 7.10). The four solutions shown correspond to w = 260, w = 520, w = 780,

and w = 1040; since these frequencies

are

close to the natural frequencies

of

261,

522,

783, and 1044, the solutions

are

almost equal to the corresponding normal

modes.

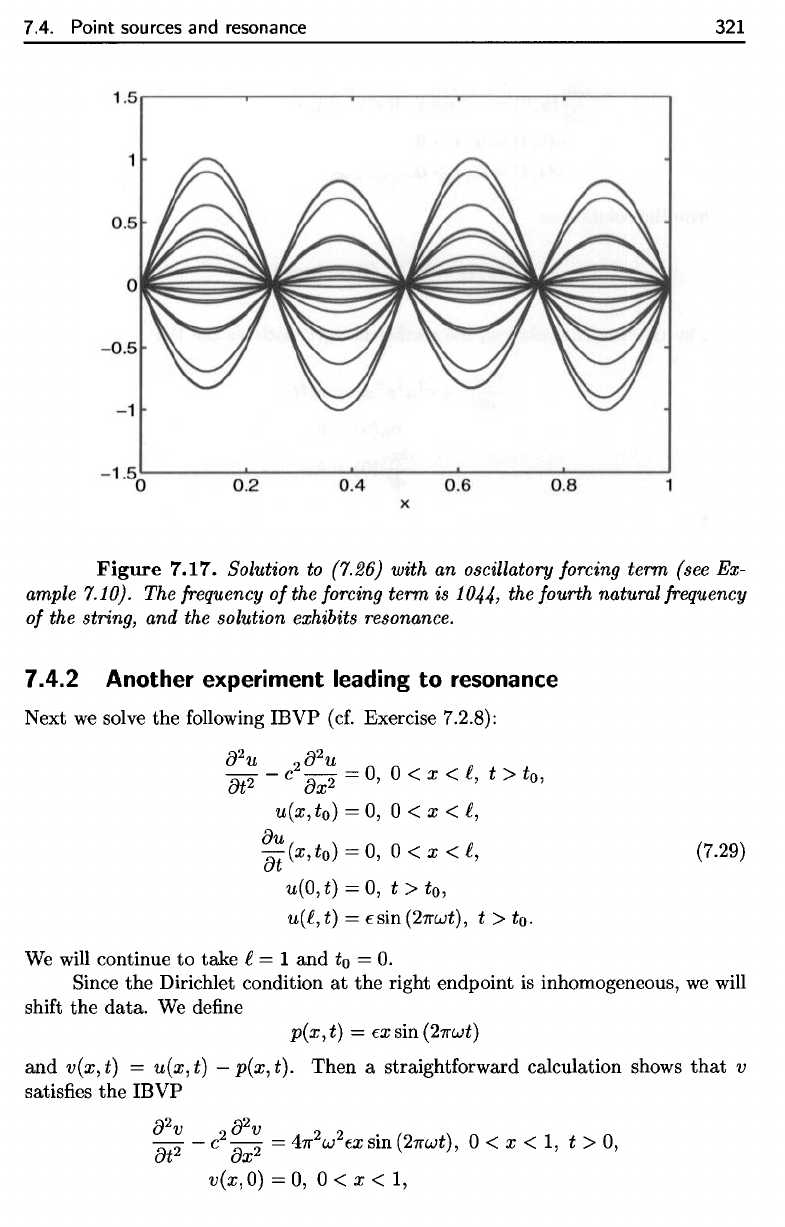
7.4. Point

sources

and

resonance

321

Figure

7.17.

Solution

to

(7.26)

with

an

oscillatory

forcing

term (see

Ex-

ample

7.10).

The

frequency

of

the

forcing

term

is

1044,

the

fourth natural

frequency

of

the

string,

and the

solution

exhibits

resonance.

We

will

continue

to

take

I

= 1 and

t

0

= 0.

Since

the

Dirichlet condition

at the

right endpoint

is

inhomogeneous,

we

will

shift

the

data.

We

define

7.4.2

Another

experiment

leading

to

resonance

solve

the

following

IBVP

(cf. Exercise 7.2.8):

and

v(x,t)

—

u(x,t)

—

p(x,t}.

Then

a

straightforward calculation shows

that

v

satisfies

the

IBVP

7.4. Point sources and resonance 321

1

.

5

r-------~-------,--------~------~--------,

0.2

0.4

0.6 0.8

x

Figure

7.17.

Solution to

{7.26}

with an oscillatory forcing term {see Ex-

ample 7.10}. The frequency

o/the/orcing

term is 1044,

the/ourth

natural frequency

0/

the string, and the solution exhibits resonance.

7.4.2 Another experiment leading to resonance

solve

the

following

IBVP

(cf.

Exercise 7.2.8):

a

2

u

2a

2

U

at

2

-

c

ax

2

= 0, 0 < x <

£,

t > to,

u(x,

to) =

0,

0 < x <

£,

au

at

(x,

to) = 0, 0 < x <

£,

u(O,

t) = 0, t > to,

u(£, t) =

lOsin

(211'wt),

t>

to.

We

will continue

to

take

£ = 1

and

to

=

O.

(7.29)

Since

the

Dirichlet condition

at

the

right endpoint

is

inhomogeneous,

we

will

shift

the

data.

We

define

p(x,

t) =

lOX

sin

(211'wt)

and

v(x,

t) =

u(x,

t) -

p(x,

t).

Then

a straightforward calculation shows

that

v

satisfies

the

IBVP

a

2

v 2 a

2

v 2 2 • ( )

at

2

-

c

ax

2

=

41T

W

EX

sm

21TWt

, 0 < x < 1,

t>

0,

v(x,O) =

0,

0 < x <

1,

and

If

u

7^

cn/2

for all n

(that

is, if

u;

is not one of the

natural

frequencies

of the

string),

then

we

obtain

322

Chapter

7.

Waves

We

write

the

solution

as

Then,

by the

usual calculation,

the

coefficient

a

n

(t)

satisfies

the

IVP

where

By

the

results

of

Section

4.2.2,

we

have

322

Chapter 7. Waves

av

at

(x, 0) =

-27fWEX,

° < X < 1,

v(O,

t) = 0, t > 0,

v(l,

t) = 0, t > 0.

We

write

the

solution as

00

v(x, t) = L an(t) sin (n7fx).

n=1

Then, by

the

usual calculation, the coefficient an(t) satisfies

the

IVP

where

and

rPa

n

2 2 2 ( )

dt

2

+ C n

7f

an

= Cn t ,

an(O)

= 0,

dan

(0)

= b

dt

n,

Cn(t)

=

211

47f

2

w

2

Exsin

(27fwt)

sin (n7fx) dx

87fW

2

E(

_l)nH

= sin

(27fwt)

n

=

en

sin

(27fwt)

1

1 .

4WE(

_l)n

b

n

= 2

(-27fWEX)

sm

(n7fx) dx = .

o n

By

the

results of Section 4.2.2,

we

have

an(t) =

~

sin

(en7ft)

+

_1_

rt

sin (cn7f(t - s))cn(s)

ds

cn7f

en7f

10

4WE(

_l)n

= 2 sin (cn7ft)

en

7f

8W

2

E(

_1)n+l

11

+ 2 sin (cn7f(t - s)) sin

(27fws)

ds.

en

0

(7.30)

(7.31)

If

W

=I-

en/2 for all n

(that

is, if W

is

not one

ofthe

natural frequencies of the string),

then

we

obtain

rt

2

10

sin (en7f(t - s)) sin

(27fws)

ds

=

7f

(c

2

n

2

_

4W2)

c;

sin

(27fwt)

- W sin (en7ft)) .

(7.32)

7.4.

Point

sources

and

resonance

323

On

the

other hand,

if

w

=

en/2,

we

obtain

The

results

are

very similar

to

those

for the

point source.

If the

externally

applied

frequency

is not a

natural

frequency

of the

string, then

no

resonance occurs.

Formula (7.32) shows, though,

that

the

amplitude

of the

vibrations gets larger

as

(jj

approaches

one of the

natural

frequencies.

If

the

external

frequency

is a

natural

frequency,

then resonance occurs,

as

indicated

by the

factor

of t in the

formula

for

a

n

(t}.

Example

7.11.

Suppose

c = 522 and

u)

= c/2 =

261,

the

fundamental

frequency

of

the

string. With

e =

0.001,

we

obtain

the

motion shown

in

Figure

7.18.

Exercises

1.

Suppose

a

string with

total

mass

of

10

g is

stretched

to a

length

of 40 cm. By

varying

the

frequency

of an

oscillatory

forcing

term until resonance occurs,

it

is

determined

that

the

fundamental

frequency

of the

string

is 500 Hz.

(a)

How

fast

do

waves travel along

the

string?

(b)

What

is the

tension

in the

string? (Hint:

See the

derivation

of the

wave

equation

in

Section 2.3.)

(c)

At

what other

frequencies

will

the

string resonate?

2.

Consider

an

iron

bar of

length

1 m,

with

a

stiffness

of k — 90 GPa and a

density

of p

=

7.2g/cm

3

.

Suppose

that

the

bottom

end (x = 1) of the bar is

fixed, and the top end is

subjected

to an

oscillatory pressure:

(a)

What

is the

smallest value

of

u;

that

causes resonance? Call this fre-

quency

(J

r

.

(b)

Find

and

graph

the

displacement

of the bar for

w

=

w

r

.

(c)

Find

and

graph

the

displacement

of the bar for

a;

=

w

r

/4.

3. If a

string

is

driven

by an

external

force

whose

frequency

equals

a

natural

frequency,

does resonance always occur? Consider

the

string

of

Example 7.10,

and

suppose

u

=

1044,

a =

1/2. Produce

a

plot like Figure 7.17. Does

resonance occur?

Why or why

not?

4.

Solve

the

IBVP

7.4. Point sources

and

resonance

323

On the other hand, if W = c:n/2,

we

obtain

i

t . sin (cmrt) t

sm

(c:n7f(t

- s)) sin

(27fws)

ds

= - - cos

(c:n7ft).

o

2c:n7f

2

(7.33)

The results are very similar

to

those for the point source.

If

the

externally

applied frequency

is

not a natural frequency of the string, then no resonance occurs.

Formula (7.32) shows, though,

that

the

amplitude of the vibrations gets larger as

W approaches one of

the

natural frequencies.

If

the

external frequency

is

a natural frequency, then resonance occurs, as

indicated by the factor of

t in the formula for an(t).

Example

7.11.

Suppose c =

522

and W =

c/2

= 261, the

fundamental

frequency

of

the string.

With

f = 0.001, we obtain the

motion

shown

in

Figure 7.18.

Exercises

1. Suppose a string with total mass of

10

g is stretched

to

a length of

40

cm. By

varying

the

frequency of an oscillatory forcing

term

until resonance occurs, it

is

determined

that

the fundamental frequency of the string

is

500

Hz.

(a)

How

fast do waves travel along the string?

(b)

What

is

the tension in the string? (Hint:

See

the derivation of

the

wave

equation in Section 2.3.)

(c) At what other frequencies will the string resonate?

2.

Consider an iron

bar

of length 1

m,

with a stiffness of k =

90

GPa

and a

density of

p =

7.2

g/cm

3

.

Suppose

that

the

bottom

end

(x

=

1)

of

the

bar

is

fixed, and the

top

end

is

subjected

to

an oscillatory pressure:

k

~~

(0,

t)

= B sin

(27rwt),

t >

o.

(a)

What

is

the

smallest value of w

that

causes resonance? Call this fre-

quency

w

r

.

(b) Find and graph the displacement of

the

bar

for w = W

r

.

(c) Find and graph the displacement of the

bar

for W =

Wr

/4.

3.

If

a string

is

driven by an external force whose frequency equals a natural

frequency, does resonance always occur? Consider the string of Example 7.10,

and suppose

W = 1044, a =

1/2.

Produce a plot like Figure 7.17. Does

resonance occur? Why or why not?

4.

Solve the IBVP

- - c

2

_

= sin (27fwt)6 x

--

8

2

u 8

2

u

(2)

8t

2

8x

2

3 '

0<

x <

1,

t>

0,

u(x,

0)

= 0, 0 < x <

1,

324

Chapter

7.

Waves

Figure

7.18.

Solution

to

(7.29) with

an

oscillatory Dirichlet condition (see

Example

7.11).

The

frequency

of

the

forcing

term

is

261,

the

fundamental

frequency

of

the

string. Shown

are 10

snapshots from

the first

fundamental period

(upper

left),

10

from

the

second fundamental period

(upper

right),

10

from

the

third (lower

left),

and

10

from

the

lower right (lower right).

The

increase

in the

amplitude

is due to

resonance.

7.5

Suggestions

for

further

reading

The

reader

can

consult Sections

5.8 and 6.7 for

further information

about

PDEs,

Fourier series,

and

finite

element methods.

There

is

another

computational

technique

that

can be

viewed

as an

alternative

324

0.01

r-----------,

0.005

-0.005

-0.01

'----------~

o 0.5

x

1

0.01

,...---------""""1

-0.01

'--

________

...J

o 0.5

x

1

Chapter

7.

Waves

0.01

r-----------,

0.005

-0.005

-0.01

'--

________

...J

o 0.5

x

1

0.01

,...---------....,

-0.01

'----------~

o 0.5

x

1

Figure

7.18.

Solution to (7.29) with an oscillatory Dirichlet condition (see

Example

7.11). The frequency

of

the forcing term is 261, the fundamental frequency

of

the string. Shown

are

10 snapshots from the first fundamental period (upper left),

10 from the second fundamental period (upper right),

10

from the third (lower left),

and 10 from the lower right (lower right). The increase in the amplitude is

due

to

resonance.

au

at

(x,O)

= 0,

0<

x <

1,

u(O,

t)

= 0, t >

0,

u(l,

t)

= 0, t > 0,

where c =

55

and w = 120. Graph several snapshots of

the

solution.

7.5 Suggestions for further reading

The

reader can consult Sections 5.8 and 6.7 for further information

about

PDEs,

Fourier series, and finite element methods.

There

is

another computational technique

that

can be viewed as

an

alternative

to finite

elements, namely,

the

method

of finite

differences.

This

method

is

very

popular

for the

wave equation

and

similar PDEs,

for the

reason

briefly

mentioned

in

the

footnote

on

Page

310. Strikwerda [47]

is an

advanced

treatment

of the finite

difference

method

for

PDEs.

Celia

and

Gray

[9]

covers both

finite

differences

and

finite

elements (including

finite

element methods

that

are not

Galerkin methods).

7.5. Suggestions

for

further

reading

325

7.5. Suggestions for further reading

325

to

finite elements, namely,

the

method of finite differences. This method

is

very

popular for the wave equation and similar PDEs, for the reason briefly mentioned

in the footnote on Page 310. Strikwerda

[47]

is

an advanced treatment of

the

finite

difference method for PDEs. Celia and Gray

[9]

covers

both

finite differences

and

finite elements (including finite element methods

that

are not Galerkin methods).

This page intentionally left blank

Most practical applications involve multiple

spatial

dimensions, leading

to

partial

differential

equations involving

two to

four

independent variables:

#1,

#2

or

#1,

xz,

t

or

xi,X2,x$,t.

The

purpose

of

this chapter

is to

extend

the

techniques

of the

last

three

chapters—Fourier

series

and finite

elements—to

PDEs involving

two or

more

spatial

dimensions.

We

begin

by

developing

the

fundamental physical models

in two and

three

dimensions.

We

then present Fourier series methods;

as we saw

earlier, these tech-

niques

are

applicable only

in the

case

of

constant-coefficient

differential

equations.

Moreover,

in

higher dimensions,

we can

only

find the

eigenfunctions explicitly when

the

computational domain

is

simple;

we

treat

the

case

of a

rectangle

and a

circular

disk

in two

dimensions.

We

then turn

to finite

element methods,

focusing

on

two-dimensional problems

and

piecewise linear

finite

elements

defined

on a

triangulation

of the

computational

domain.

8.1

Physical models

in two or

three

spatial

dimensions

The

derivation

of the

physical models

in

Chapter

2

depended

on the

fundamental

theorem

of

calculus. Using this result,

we

were able

to

relate

a

quantity

defined

on

the

boundary

of an

interval

(force

acting

on a

cross-section

or

heat

energy

flowing

across

a

cross-section,

for

example)

to a

related quantity

in the

interior

of the

interval.

In

higher dimensions,

the

analogue

of the

fundamental theorem

of

calculus

is

the

divergence theorem, which

relates

a

vector

field

acting

on the

boundary

of a

domain

to the

divergence

of the

vector

field in the

interior.

We

begin

by

explaining

the

divergence theorem

and

proceed

to

apply

it to a

derivation

of the

heat equation.

We

must

first

establish some notation.

327

Chapter

8

Jgihlems

in

multiple

spatial

dimensions

Chapter 8

multiple

•

menslons

Most practical applications involve multiple spatial dimensions, leading

to

partial

differential equations involving two

to

four independent variables:

Xl,

X2

or

Xl,

X2,

t

or

Xl,

X2,

X3,

t.

The purpose of this chapter is

to

extend

the

techniques of

the

last

three

chapters-Fourier

series and finite

elements-to

PDEs involving two or more

spatial dimensions.

We

begin by developing the fundamental physical models in two and three

dimensions.

We

then

present Fourier series methods; as

we

saw earlier, these tech-

niques are applicable only in the case

of

constant-coefficient differential equations.

Moreover, in higher dimensions,

we

can only find the eigenfunctions explicitly when

the

computational domain

is

simple;

we

treat

the case of a rectangle and a circular

disk in two dimensions.

We

then

turn

to

finite element methods, focusing on two-dimensional problems

and

piecewise linear finite elements defined on a triangulation of

the

computational

domain.

8.1 Physical models

in

two

or

three spatial

dimensions

The

derivation of the physical models in Chapter 2 depended on

the

fundamental

theorem of calculus. Using this result,

we

were able

to

relate a quantity defined on

the

boundary of

an

interval (force acting on a cross-section or

heat

energy flowing

across a cross-section, for example)

to

a related quantity in the interior of the

interval.

In higher dimensions,

the

analogue of

the

fundamental theorem of calculus

is

the

divergence theorem, which relates a vector field acting on the boundary

of

a

domain

to

the divergence of the vector field in the interior.

We

begin by explaining

the

divergence theorem and proceed to apply

it

to

a derivation of

the

heat equation.

We

must first establish some notation.

327

Gockenbach M.S. Partial Differential Equations. Analytical and Numerical Methods

Подождите немного. Документ загружается.