Gockenbach M.S. Partial Differential Equations. Analytical and Numerical Methods
Подождите немного. Документ загружается.

308
Chapter
7.
Waves
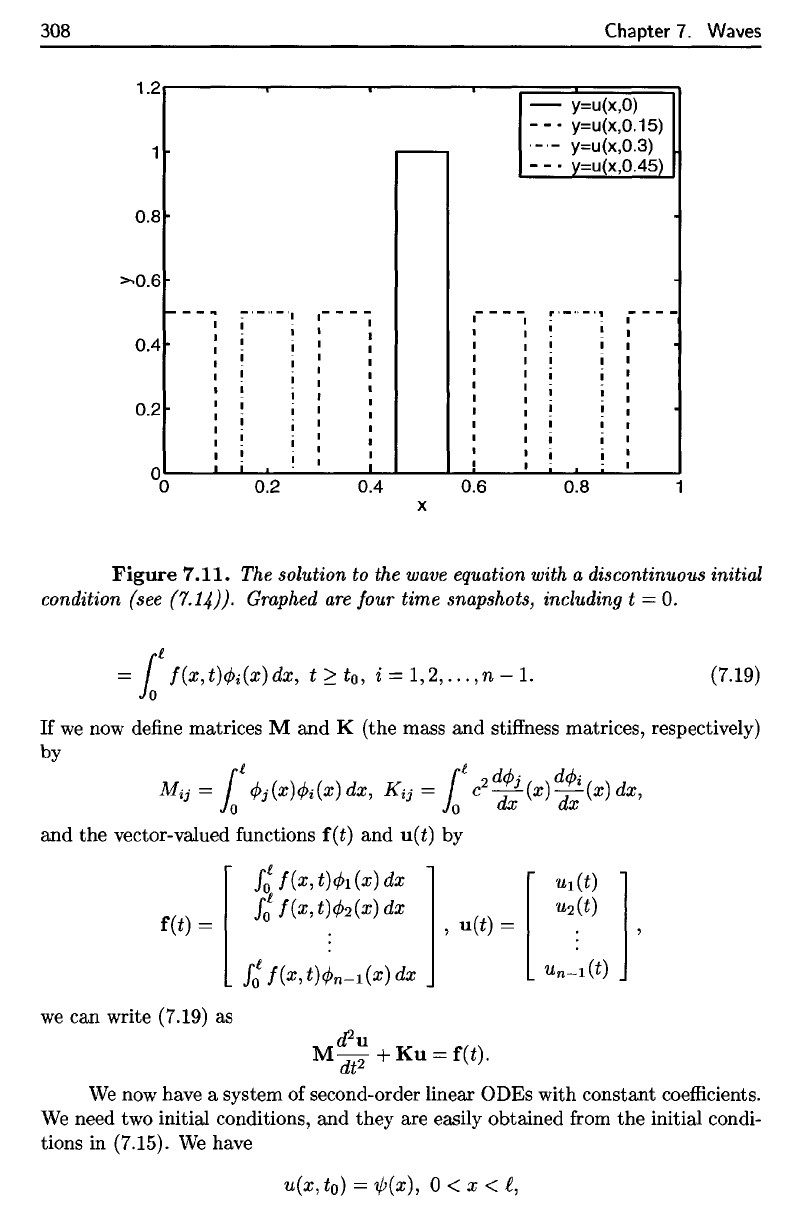
Figure
7.11.
The
solution
to the
wave
equation with
a
discontinuous initial
condition
(see
(7.14)).
Graphed
are
four time snapshots, including
t = 0.
we
can
write (7.19)
as
We
now
have
a
system
of
second-order linear ODEs with
constant
coefficients.
We
need
two
initial conditions,
and
they
are
easily obtained
from
the
initial condi-
tions
in
(7.15).
We
have
If
we now
define
matrices
M and K
(the mass
and
stiffness
matrices,
respectively)
bv
and the
vector-valued functions
f
(t)
and
u(£)
by
308
Chapter
7.
Waves
1.2
-
y=u(x,O)
-_ .
y=u(x,0.15)
-
.
_.
- y=u(x,0.3)
-
-.
y=u(x,0.45)
0.8
>'0.6
-
--
._
..
_'.
-
--
--
--
'-"-"
-
--
•
•
0.4
•
•
•
•
•
•
•
•
0.2
•
•
•
•
i
i
•
•
0.2 0.4
0.6 0.8
x
Figure
7.11.
The solution
to
the wave equation with a discontinuous initial
condition (see
(7.14)). Graphed
are
four time snapshots, including t =
O.
=
lot
f(x,
t)¢i(X)
dx, t
"2:
to,
i = 1,2,
...
, n -
l.
(7.19)
If
we
now define matrices M
and
K
(the
mass
and
stiffness matrices, respectively)
by
rt
rt
2
d¢j
d¢i
Mij
=
10
¢j
(X)¢i (x) dx,
Kij
=
10
c dx (x) dx (x) dx,
and
the
vector-valued functions f(t)
and
u(t) by
[
I~
~~::
:~:~~:~~:
I [
~~~:~
1
f(t) = , u(t) = . ,
f~
f(x,
t)¢n-l
(x) dx Un-·l(t)
we
can
write (7.19) as
~u
M dt
2
+
Ku
= f(t).
We now have a
system
of
second-order linear
ODEs
with
constant
coefficients.
We need two initial conditions,
and
they
are
easily
obtained
from
the
initial condi-
tions in (7.15). We have
u(x,
to)
=
1jJ(x),
0 < x <
£,
7.3.
Finite
element methods
for the
wave equation
309
and
T/>(X)
can be
approximated
by its
linear interpolant:
We
therefore require
that
Similarly,
we
require
(7.20)
To
apply
one of the
numerical methods
for
ODEs
that
we
studied
in
Chapter
4,
we
must
first
convert (7.20)
to a first-order
system.
We
will
define
(y,z
€
R
11
"
1
).
Then
47
As
we
discussed
in
Section 6.4,
we do not
actually
form
the
inverse matrix
M
1
.
Instead,
when
the
action
of
M^
1
is
needed,
we
solve
the
appropriate
linear system.
These lead
to the
initial conditions
We
therefore obtain
the
IVI
where
47
A = -M
1
K
and
g(t)
= M
1
f(t).
We
also have initial conditions:
7.3. Finite element methods for
the
wave equation
and
'IjJ(x)
can be approximated by its linear interpolant:
n-l
'IjJ(x)
==
L
'IjJ(Xi)¢>i(X).
i=l
We
therefore require
that
Similarly,
we
require
dUi
dt(t
o
)
=
,(Xi)'
These lead
to
the initial conditions
u(t
o
)
=
Yo
=
[
'IjJ(xd
1
'IjJ(X2)
'IjJ(x~-d
'
du
-(to)
=
Zo
=
dt
We
therefore obtain the IVP
~u
M dt
2
+Ku
= f(t),
t>
to,
u(t
o
)
=
Yo,
u'(t
o
) =
Zoo
309
[
,(Xl)
1
,(X2)
'(X~-l)
.
(7.20)
To apply one of the numerical methods for ODEs
that
we
studied in Chapter
4,
we
must first convert (7.20)
to
a first-order system.
We
will define
(y,z
ERn-I).
Then
y(t) = u(t),
du
z(t) = dt
(t)
dy
dt = z,
dz
~u
dt dt
2
=
M-
I
(-Ku
+ f(t))
=
-M-1Ky
+
M-1f(t)
=
Ay
+ g(t),
where
47
A =
-M-1K
and g(t) =
M-lf(t).
We
also have initial conditions:
y(to) = u(to) =
Yo,
du
z(to) = dt (to) =
zoo
47
As
we
discussed in Section 6.4,
we
do
not
actually form
the
inverse
matrix
M-
1
.
Instead,
when
the
action
of
M-l
is needed,
we
solve
the
appropriate
linear system.

310
Chapter
7.
Waves
48
However,
in a
sense,
the use of the finite
element obscures
the
distinction between
an
implicit
and an
explicit method.
The
mass matrix couples
the
derivatives,
and so, to
advance
a
time-
stepping
method,
it is
necessary
to
solve
a
linear system,
even
in an
explicit method. This means
that explicit methods
are no
more
efficient
than implicit methods.
The
same
was
true
in the
case
of
the
heat equation, with,
however,
a key
difference.
For the
heat equation,
the
stability requirement
is
such that
it is not
advantageous
to use
explicit methods anyway,
and so the
coupling introduced
by the finite
element method
is not
important.
For the
wave
equation, explicit
finite
difference
methods
do not
couple
the
derivatives,
and
there
is no
need
to
solve
a
linear system
to
take
a
time
step.
For
this reason,
finite
difference
methods
are
preferred
for the
wave
equation
if the
geometry
is
simple.
Finite
element methods
still
have
advantages
for
complicated geometries.
with
c = 522 and
The
resulting solution
is
quite smooth,
so the finite
element method
should
work
well.
We use a
regular
grid
with
n
= 20
subintervals
(h =
1/n),
and
apply
the RK4
method
to
integrate
the
resulting ODEs.
The
fundamental
frequency
of
the
string
is
We
have thus obtained
the
(In
—
2) x
(In
—
2)
system
of
IVPs
We
can now
apply
any of the
numerical methods
that
we
have previously learned,
such
as
Euler's
method, RK4,
or an
adaptive
scheme.
Just
as in the
case
of the
heat
equation, stability
is an
issue.
If the
time step
At is
chosen
to be too
large relative
to the
spatial
mesh size
h,
then
the
approximate
solution computed
by the
time stepping method
can
"blow
up"
(i.e. increase without
bound).
For the
heat
equation, using Euler's method,
we
needed
At =
O(h
2
).
This
required such
a
large number
of
time
steps
that
it was
advantageous
to use
special methods (such
as the
backward
Euler
method)
for the
sake
of
efficiency.
The
requirement
on At is not so
stringent
when solving
the
wave equation;
we
just
need
At =
O(h/c}.
For
this reason,
we
usually
use
explicit methods
to
solve
the
system
of
ODEs arising
from
the
wave equation;
the
improved stability properties
of
implicit
methods
are not
really
needed.
48
We
must keep
the
stability requirement
in
mind,
though.
If, in
applying
(7.20)
to
approximate
a
solution
to the
wave equation,
we
notice
that
the
approximate solution
is
growing unreasonably
in
amplitude, then
the
time step must
be
decreased.
Example
7.7.
We
will
solve
the
IBVP
310
We
have thus obtained the (2n -
2)
x (2n -
2)
system of IVPs
<!x
dt
dz
dt
z,
y(t
o
)
Ay
+ g(t),
z(t
o
)
Yo,
zoo
Chapter 7. Waves
(7.21)
We
can now apply any of
the
numerical methods
that
we
have previously learned,
such as Euler's method,
RK4, or
an
adaptive scheme.
Just
as in the case of the
heat
equation, stability
is
an
issue. If the time step
!:l.t
is
chosen
to
be too large relative
to
the spatial mesh size
h,
then
the
approximate
solution computed by the time stepping method can "blow up" (i.e. increase without
bound). For the heat equation, using Euler's method,
we
needed
!:l.t
= O(h2).
This required such a large number of time steps
that
it
was advantageous to use
special methods (such as the backward Euler method) for the sake of efficiency.
The
requirement
on
!:l.t
is not so stringent when solving the wave equation;
we
just
need
!:l.t
=
O(hlc).
For this reason,
we
usually use explicit methods to solve the system of
ODEs arising from
the
wave equation; the improved stability properties of implicit
methods are not really needed.
48
We
must keep
the
stability requirement in mind,
though.
If,
in applying (7.20) to approximate a solution to the wave equation,
we
notice
that
the
approximate solution
is
growing unreasonably in amplitude, then
the
time step must be decreased.
Example
7.7.
We will solve the
lBVP
f)
2
u
f)
2
u
f)t
2
-
c
2
f)x
2
= 0, ° < x <
1,
t>
0,
u(x,O)
= 'IjJ(x),
0<
x <
1,
f)u
f)t (x,O)
= 0,
0<
x < 1,
(7.22)
u(O, t) = 0, t > 0,
u(l,
t)
= 0, t > °
with c =
522
and
'IjJ(x)
= O.01x(l -
x).
The resulting solution is quite smooth,
so
the finite element method should work
well. We use a regular grid with n
=
20
subintervals (h =
lin),
and apply the
RK4
method to integrate the resulting ODEs. The fundamental frequency
of
the string
is
48However, in a sense,
the
use of
the
finite element obscures
the
distinction between
an
implicit
and
an
explicit
method.
The
mass
matrix
couples
the
derivatives,
and
so,
to
advance a time-
stepping
method,
it
is necessary
to
solve a linear system, even in
an
explicit method.
This
means
that
explicit
methods
are no more efficient
than
implicit
methods.
The
same
was
true
in
the
case
of
the
heat
equation,
with,
however, a key difference.
For
the
heat
equation,
the
stability requirement
is such
that
it
is
not
advantageous
to
use explicit
methods
anyway,
and
so
the
coupling
introduced
by
the
finite element
method
is
not
important.
For
the
wave equation, explicit finite difference
methods
do
not
couple
the
derivatives,
and
there
is no need
to
solve a linear
system
to
take
a
time
step. For
this
reason, finite difference
methods
are preferred for
the
wave equation if
the
geometry
is simple.
Finite
element
methods
still have advantages for complicated geometries.
7.3.
Finite element methods
for the
wave
equation
311
c/(1i}
=
261,
making
the
fundamental
period
We
compute
the
motion
of
the
string over
one
period,
using
50
steps
(At
=
T/50J.
The
results
are
shown
in
Figure
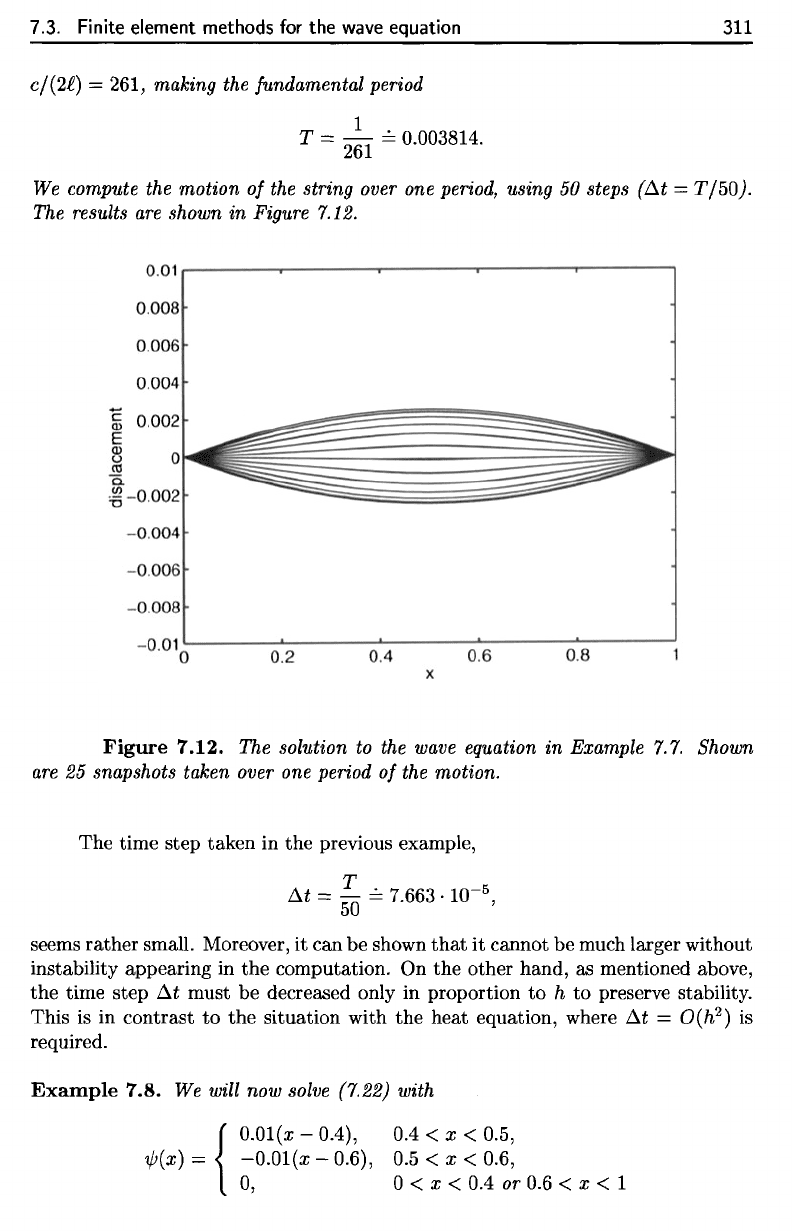
7.12.
Figure
7.12.
The
solution
to the
wave
equation
in
Example 7.7. Shown
are
25
snapshots taken over
one
period
of the
motion.
The
time step taken
in the
previous example,
seems
rather small. Moreover,
it can be
shown
that
it
cannot
be
much larger without
instability
appearing
in the
computation.
On the
other
hand,
as
mentioned above,
the
time step
At
must
be
decreased only
in
proportion
to h to
preserve stability.
This
is in
contrast
to the
situation with
the
heat equation, where
At =
O(/i
2
)
is
reauired.
Example
7.8.
We
will
now
solve
(7.22) with
7.3. Finite element methods for
the
wave equation
c/(2f) = 261, making the fundamental period
T
1.
=
261
= 0.003814.
311
We compute the motion
of
the string over one period, using
50
steps
{!:1t
=
T/50}.
The results
are
shown
in
Figure 7.12.
0.
01
,------..-----.----...,.----.,.-----,
o.
0.
006
0.004
~
0.
002
E
Q)
:\l
a.
:6
- 0.
002
- 0.004
- 0.
006
- 0.
008
0.2
0.4
0.6
0.8
x
Figure
7.12. The solution to the wave equation
in
Example
7.7.
Shown
are
25 snapshots taken over one period
of
the motion.
The time step taken in the previous example,
AT.
7
-5
Uot
=
50
= .663·
10
,
seems
rather
small. Moreover,
it
can
be
shown
that
it
cannot be much larger without
instability appearing in
the
computation. On the other hand, as mentioned above,
the
time step
!:1t
must be decreased only in proportion to h to preserve stability.
This is in contrast to
the
situation with the heat equation, where
!:1t
=
O(h2)
is
required.
Example
7.S. We will now solve
{7.22}
with
{
O.Ol(x - 0.4), 0.4 < x < 0.5,
¢(x)
=
-O.Ol(x
- 0.6), 0.5 < x < 0.6,
0,
0 < x < 0.4 or 0.6 < x < 1
312
Chapter
7.
Waves
(compare
Example 7.3). Since
the
initial displacement
if}
is not
very smooth
(V>
is
continuous
but its
derivative
has
singularities),
our
comments
at the
beginning
of
the
section suggest that
it may be
difficult
to
accurately compute
the
wave
motion
using
finite
elements.
We
use the
same spatial mesh
(h
=
1/20,),
time-stepping algorithm (RK4),
and
time-step
(£±t
=
T/50J
as in the
previous example.
In
Figure 7.13,
we
show
three
snapshots
of the
solution.
We
already
know
how the
solution should look:
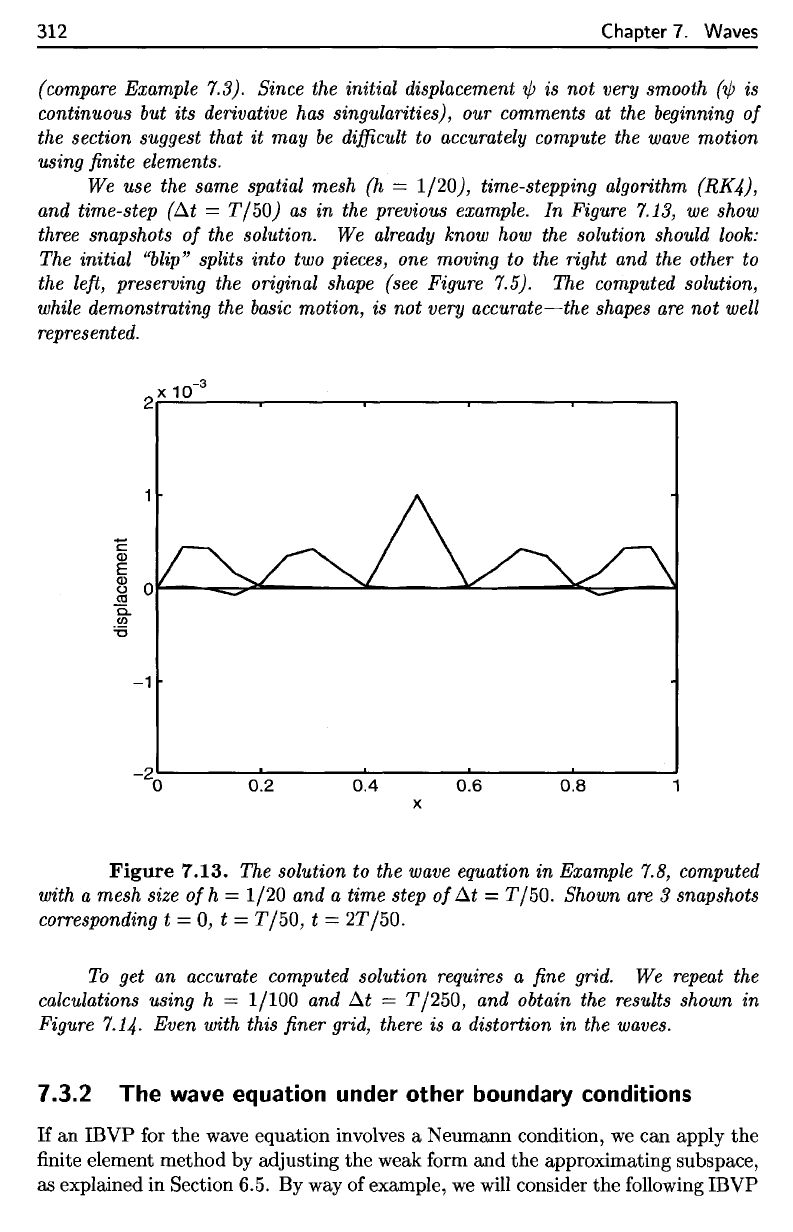
The
initial
"blip"
splits
into
two
pieces,
one
moving
to the
right
and the
other
to
the
left,
preserving
the
original
shape
(see Figure 7.5).
The
computed
solution,
while
demonstrating
the
basic
motion,
is not
very
accurate—the
shapes
are not
well
represented.
Figure
7.13.
The
solution
to the
wave equation
in
Example 7.8, computed
with
a
mesh size
of
h =
1/20
and a
time
step
of
A£
=
T/50.
Shown
are 3
snapshots
corresponding
t =
Q,t
=
T/50
;
t =
2T/50.
To
get an
accurate computed solution requires
a fine
grid.
We
repeat
the
calculations using
h =
1/100
and
At
=
T/250,
and
obtain
the
results shown
in
Figure
7.14-
Even
with this
finer
grid, there
is a
distortion
in the
waves.
7.3.2
The
wave
equation
under
other
boundary
conditions
If
an
IBVP
for the
wave
equation
involves
a
Neumann
condition,
we can
apply
the
finite
element method
by
adjusting
the
weak form
and the
approximating
subspace,
as
explained
in
Section
6.5.
By way of
example,
we
will
consider
the
following
IBVP
312
Chapter 7. Waves
(compare Example 1.3). Since the initial displacement '¢
is
not very smooth
('¢
is
continuous but its derivative has singularities), our comments at the beginning
of
the section suggest that
it
may
be
difficult
to
accurately compute the wave motion
using finite elements.
We use the same spatial mesh (h
=
1/20),
time-stepping algorithm (RK4) ,
and time-step
(ilt
= T / 50)
as
in the previous example. In Figure 7.13,
we
show
three snapshots
of
the solution. We already know how the solution should
look:
The initial "blip" splits into two pieces, one moving to the right and the other to
the left, preserving the original shape (see Figure 7.5). The computed solution,
while demonstrating the basic motion, is not very
accurate-the
shapes
are
not
well
represented.
E
Ql
E
Ql
o
(1J
0.
!I)
'6
-1
-20~------~-------L--------~------~------~
0.2 0.4 0.6 0.8
1
x
Figure
7.13.
The solution to the wave equation in Example 7.8, computed
with a mesh size
of
h = 1/20 and a time step
of
ilt
=
T/50.
Shown
are
3 snapshots
corresponding
t =
0,
t =
T/50,
t =
2T/50.
To
get an accurate computed solution requires a fine grid. We repeat the
calculations using h
= 1/100 and
ilt
= T /250, and obtain the results shown in
Figure 7.14. Even with this finer grid, there
is
a distortion in the waves.
7.3.2 The
wave
equation under other boundary conditions
If
an IBVP for
the
wave equation involves a Neumann condition,
we
can apply the
finite element method by adjusting the weak form and the approximating subspace,
as explained in Section 6.5. By way of example,
we
will consider the following IBVP
7.3. Finite element methods
for the
wave
equation
313
Figure
7.14.
The
solution
to the
wave
equation
in
Example 7.8, computed
with
a
mesh size
of
h
=
1/100
and a
time
step
of At =
T/250.
Shown
are 3
snapshots
corresponding
t =
0,
t
—
T/50,
t =
2T/50.
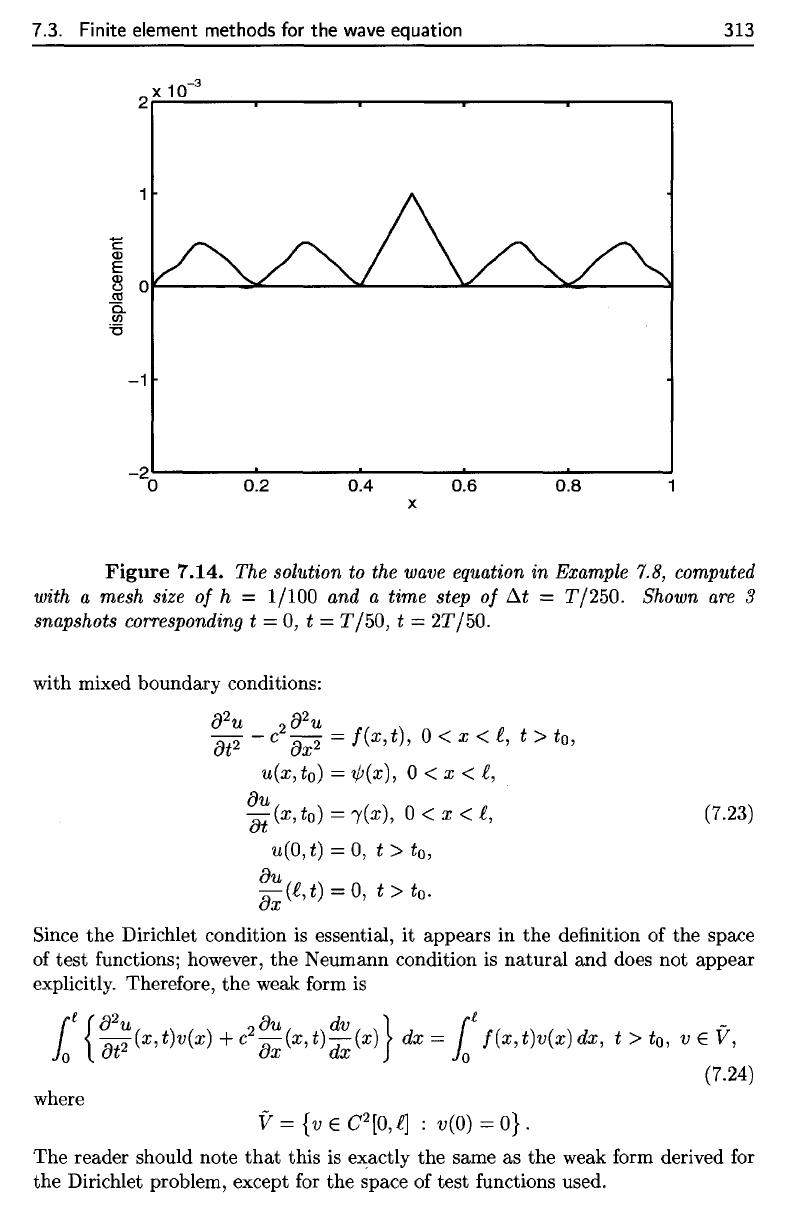
with mixed boundary conditions:
Since
the
Dirichlet condition
is
essential,
it
appears
in the
definition
of the
space
of
test
functions; however,
the
Neumann condition
is
natural
and
does
not
appear
explicitly. Therefore,
the
weak
form
is
where
The
reader should note
that
this
is
exactly
the
same
as the
weak
form
derived
for
the
Dirichlet problem, except
for the
space
of
test
functions used.
7.3. Finite element methods
for
the
wave
equation
c
Q)
E
Q)
(.)
ttl
Ci
en
'5
-1
-2~------~------~--------~------~------~
o
0.2 0.4 0.6
0.8
x
313
Figure
7.14.
The
solution
to
the
wave
equation in Example
7.B,
computed
with a mesh size of
h = 1/100 and a time step of
6..t
= T /250. Shown
are
3
snapshots corresponding t = 0, t = T /50, t =
2T
/50.
with mixed boundary conditions:
a
2
u 2 a
2
u
at
2
-
c
ax
2
=
f(x,
t),
0<
x <
e,
t>
to,
u(x,
to)
=
'I/J(x),
0<
x <
e,
au
at
(x,
to)
= l'(x),
0<
x <
e,
(7.23)
u(O,
t) = 0,
t>
to,
au
ax
(e,
t) = 0, t >
to.
Since
the
Dirichlet condition
is
essential,
it
appears in the definition of the space
of
test
functions; however, the Neumann condition
is
natural
and
does not appear
explicitly. Therefore,
the
weak form
is
1t
{
~:~
(x, t)v(x) + c
2
~:
(x, t)
:~
(x)
} dx =
l'
f(x,
t)v(x) dx, t >
to,
v E
ii,
(7.24)
where
ii
=
{v
E C
2
[0,e]
:
v(O)
=
O}.
The
reader should note
that
this
is
e~actly
the same as the weak form derived for
the Dirichlet problem, except for
the
space of test functions used.
314
Chapter
7.
Waves
To
apply
the
Galerkin method,
we
establish
a
grid
and
choose
the finite
element subspace consisting
of all
continuous piecewise linear
functions
(relative
to the
given mesh) satisfying
the
Dirichlet condition
at the
left
endpoint.
This
subspace
can be
represented
as
The
only
difference
between
S
n
and
S
n
,
the
subspace used
for the
Dirichlet problem,
is the
inclusion
of the
basis
function
(f)
n
corresponding
to the
right endpoint.
For
simplicity,
we
will
use a
regular grid
in the
following
calculations.
The
calculation then proceeds
just
as for the
Dirichlet problem, except
that
there
is an
extra
basis
function
and
hence
an
extra
unknown
and
corresponding
equation.
We
write
for
the
approximation
to the
solution
u(x,
t).
Substituting into
the
weak
form
yields
the
equations
where
M 6
R
nxn
,
K €
R
nxn
,
and
f(t)
€
R
n
.
The
mass matrix
M is
tridiagonal,
with
the
following
nonzero entries:
The
stiffness
matrix
K is
also tridiagonal, with
the
following
nonzero entries:
314
Chapter 7. Waves
To apply the Galerkin method,
we
establish a grid
o =
Xo
<
Xl
<
X2
< ... <
Xn
= C
and choose the finite element subspace consisting of all continuous piecewise linear
functions (relative
to
the
given mesh) satisfying the Dirichlet condition
at
the left
endpoint. This subspace can be represented as
The
only difference between Sn and Sn, the subspace used for the Dirichlet problem,
is
the
inclusion of the basis function
¢n
corresponding
to
the right endpoint. For
simplicity,
we
will use a regular grid in the following calculations.
The
calculation then proceeds
just
as for
the
Dirichlet problem, except
that
there
is
an
extra
basis function
and
hence an
extra
unknown and corresponding
equation.
We
write
n
vn(x,
t)
= L Ui(t)¢i(X)
i=l
for
the
approximation to the solution
u(x,
t). Substituting into the weak form yields
the equations
_ d
2
u _ _
M dt
2
+
Ku
=
f(t),
where
ME
Rnxn, K E Rnxn, and
ret)
ERn.
The mass matrix M
is
tridiagonal,
with the following nonzero entries:
i
=
1,2,
...
,n
- 1,
MHI,i
=
Mi,HI,
i =
1,2,
...
, n - 1.
The
stiffness matrix K
is
also tridiagonal, with the following nonzero entries:
7.3.
Finite
element methods
for the
wave
equation
315
The
IVP
Finally,
the
load vector
f
(t)
is
given
by
Having derived
the
system
of
ODEs,
the
formulation
of the
initial
conditions
is
just
as
before:
is
then converted
to the first-order
system
where
A =
-M^K
and
g(t)
=
M~
l
f(t).
Example
7.9.
We
will
compute
the
motion
of
the
string
in
Example 7.7, with
the
only
change
being
that
the
right
end
of
the
string
is now
assumed
to be
free
to
move
vertically.
The
IBVP
is
7.3. Finite element methods for
the
wave equation
315
Finally,
the
load vector f(t) is given
by
!i(t)
=
fal
f(x,t)¢i(x)dx,
i = 1,2,
...
,n.
Having derived
the
system
of
ODEs,
the
formulation
of
the
initial conditions
is
just
as
before:
The
IVP
-
cPu
- -
M dt
2
+
Ku
= f(t), t >
to,
u(to) =
Yo,
u'(t
o
) =
Zo
is
then
converted
to
the
first-order
system
dy
dt = z,
y(t
o) =
Yo,
dz -
dt
=
Ay
+ g(t), z(to) =
Zo,
where A =
_M~l:K
and
g(t) =
M~1f(t).
Exalllple
7.9.
We
will compute the motion
of
the string in Example 7.7, with the
only change
being
that the right end
of
the string is now assumed to
be
free
to move
vertically. The
IBVP
is
a
2
u 2 a
2
u .
at
2
-
c
ax
2
= 0, ° < x <
1,
t >
0,
u(x,O)=x(l-x),O<x<l,
au
at
(x, 0) = 0, ° < x < 1,
u(O,t) = 0,
t>
0,
au
ax
(1,
t)
= 0, t > 0,
316
Chapter
7.
Waves
with
c =
522.
The
only
change from
the
earlier calculations
is
that there
is an
extra
row and
column
in the
mass
and
stiffness
matrix.
We
will
again
use n = 20
subintervals
in the
spatial mesh
(h =
1/20,).
The
fundamental period
is now
We
use the RK4
algorithm
and 100
time steps
to
compute
the
motion over
one
period
(At
=
T/lOOj.
The
results
are
shown
in
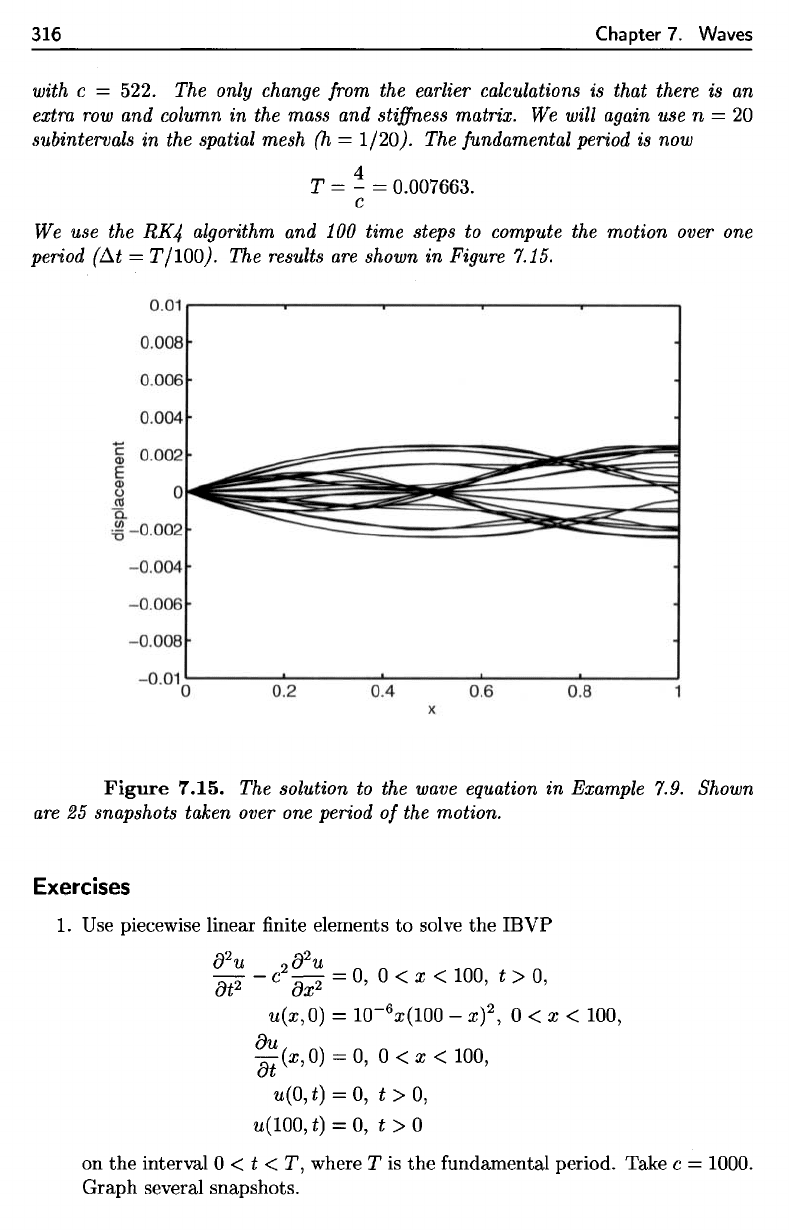
Figure 7.15.
Figure
7.15.
The
solution
to the
wave equation
in
Example 7.9. Shown
are
25
snapshots taken over
one
period
of the
motion.
Exercises
1.
Use
piecewise linear
finite
elements
to
solve
the
IBVP
on
the
interval
0 < t < T,
where
T is the
fundamental period. Take
c =
1000.
Graph several
snapshots.
316
Chapter 7. Waves
with c = 522. The only change from the earlier calculations is that there is an
extra row and column
in
the mass and stiffness matrix. We will again use n = 20
subintervals
in
the spatial mesh
(h
=
1/20).
The fundamental period is now
T =
~
= 0.007663.
c
We use the
RK4
algorithm and 100
time
steps to compute the motion over one
period (Llt
= TIlOO). The results are shown
in
Figure
7.15.
0.
01
0.
008
0.
006
0.
004
C
0.002
~
Q)
E
0
......-
~
~
~
-
Q)
0
cQ
~
-
a.
:6
- 0.
002
--=::::::::::-
- 0.
004
- 0.
006
- 0.
008
- 0.
01
0 0.2
0.4
0.6 0.8
x
Figure
7.15.
The solution to the wave equation
in
Example 7.9. Shown
are
25 snapshots taken over one period
of
the motion.
Exercises
1. Use piecewise
linear
finite
elements
to
solve
the
IBVP
fPu 2 fpu
at
2
-
c
ax
2
= 0, 0 < x < 100, t > 0,
u(x,O) = 1O-
6
x(100
-
X)2,
0 < X < 100,
au
at
(x, 0) = 0, 0 < x < 100,
u(O,
t) = 0, t > 0,
u(lOO,
t)
= 0, t > 0
on
the
interval
0 < t <
T,
where
T is
the
fundamental
period.
Take
c = 1000.
Graph
several
snapshots.

7.3. Finite element methods
for the
wave
equation
317
2.
Repeat
the
previous exercise, assuming
the PDE is
inhomogeneous with right-
hand side equal
to the
constant
—100.
3.
(Cf. Exercise
7.2.2.)
Consider
a
string
of
length 50cm, with
c =
400cm/s.
Suppose
that
the
string
is
initially
at
rest, with both ends
fixed, and
that
it
is
struck
by a
hammer
at its
center
so as to
induce
an
initial velocity
of
(a)
How
long does
it
take
for the
resulting wave
to
reach
the
ends
of the
string?
(b)
Formulate
and
solve
the
IBVP
describing
the
motion
of the
string.
Use
the finite
element method with
RK4 or
some other numerical method
for
solving
the
system
of
ODEs.
(c)
Plot
several snapshots
of the
string, showing
the
wave
first
reaching
the
ends
of the
string.
Verify
your answer
to 3a.
4.
Repeat
Exercise
3,
assuming
that
the
right
end of the
string
is
free
to
move
vertically.
5.
Solve (7.14) using
the finite
element method,
and try to
reproduce Figure
7.11.
How
small must
h
(the length
of the
subintervals
in the
mesh)
be to
obtain
a
good graph?
6.
(Cf. Example 7.6.) Consider
a
steel
bar of
length
1 m, fixed at the top (x = 0)
with
the
bottom
end (x = 1)
free
to
move. Suppose
the bar is
stretched,
by
means
of a
downward pressure applied
to the
free
end,
to a
length
of
1.002
m,
and
then released. Using
the finite
element method, compute
the
motion
of
the
bar, given
that
the
type
of
steel
has
stiffness
k = 195 GPa and
density
p
=
7.9g/cm
3
.
Produce
a
graph analogous
to
Figure 7.9.
7.
Consider
a
heterogeneous
bar
with
the top end fixed and the
bottom
end
free.
According
to the
derivation
in
Section 2.2,
the
displacement
u(x,t)
of the bar
satisfies
the
IBVP
(a)
Formulate
the
weak
form
of
(7.25).
7.3. Finite element methods for
the
wave equation
317
2.
Repeat the previous exercise, assuming
the
PDE
is
inhomogeneous with right-
hand side equal to the constant
-100.
3. (Cf. Exercise 7.2.2.) Consider a string of length 50cm, with c = 400cm/s.
Suppose
that
the
string
is
initially
at
rest, with
both
ends fixed, and
that
it
is
struck by a hammer
at
its center so as
to
induce
an
initial velocity of
{
-20,
24
< x <
26,
'Y(x)
=
0,
0
:::;
x
:::;
24
or
26
:::;
x
:::;
50.
(a)
How
long does
it
take for the resulting wave
to
reach
the
ends of the
string?
(b) Formulate and solve the IBVP describing the motion of the string. Use
the
finite element method with RK4
or
some other numerical method for
solving
the
system of ODEs.
(c)
Plot several snapshots of the string, showing
the
wave first reaching the
ends of the string. Verify your answer
to
3a.
4. Repeat Exercise 3, assuming
that
the right end of the string
is
free to move
vertically.
5.
Solve (7.14) using the finite element method, and
try
to reproduce Figure
7.11. How small must h (the length of the subintervals in
the
mesh) be
to
obtain a good graph?
6.
(Cf. Example 7.6.) Consider a steel
bar
of length 1 m, fixed
at
the top
(x
=
0)
with
the
bottom
end
(x
=
1)
free to move. Suppose the
bar
is
stretched, by
means of a downward pressure applied to the free end, to a length of 1.002 m,
and then released. Using the finite element method, compute
the
motion of
the bar, given
that
the type of steel has stiffness k = 195
GPa
and density
p =
7.9g/cm
3
.
Produce a graph analogous to Figure 7.9.
7.
Consider a heterogeneous
bar
with
the
top end fixed and the
bottom
end free.
According to
the
derivation in Section 2.2, the displacement u(x, t) of
the
bar
satisfies the IBVP
a
2
u a (
au)
p(x)
at
2
-
ax
k(x)
ax
=
f(x,
t), 0 < x <
e,
t >
to,
u(x,
to)
=
'lj!(x),
0 < x <
e,
au
at
(x,
to)
= 'Y(x), 0 < x <
e,
(7.25)
u(O,
t) = 0, t >
to,
au
8x(e,t)
=0,
t>to.
(a) Formulate the weak form of (7.25).
