Gockenbach M.S. Partial Differential Equations. Analytical and Numerical Methods
Подождите немного. Документ загружается.


298
Chapter
7.
Waves
The
solution
is
periodic with period
Twenty-five
snapshots
of
the
solution (taken during
one
period)
are
shown
in
Figure
7.6.
The
effect
of
the
external
force
on the
motion
of
the
string
is
clearly
seen.
(The
reader
should solve Exercise
1 if it is not
clear
how the
string
would
move
in the
absence
of the
external force.)
Figure
7.6.
Twenty-five
snapshots
of the
vibrating string from Example
7.4-
We
now
consider
an
example
in
which
one of the
boundary conditions
is in-
homogeneous.
As
usual,
we use the
method
of
shifting
the
data.
Example
7.5.
Consider
a
string
of
length
100 cm
that
has one end fixed at x = 0,
with
the
other
end
free
to
move
in the
vertical direction
only
(tied
to a
frictionless
pole,
for
example).
Let the
wave
speed
in the
string
be c =
2000
cm/5.
45
Suppose
the
free
end is
"flicked,"
that
is,
moved
up and
down
rapidly,
according
to the
formula
u(100,t)
=
/(*),
where
45
The
fundamental
frequency
is
then
By
comparison,
the
lowest tone
of a
piano
has
frequency
27.5
Hz.
298
Chapter 7. Waves
The solution is periodic with period
2n 50
=
cn
/25
c
Twenty-five snapshots
oj
the solution (taken during one period)
are
shown in Figure
7.6. The effect
oj
the external
Jorce
on the motion
oj
the string is clearly seen. (The
reader should solve Exercise
1
iJ
it
is
not
clear how the string would move in the
absence
oj
the external Jorce.)
0
.
1~------r-------~--~--~------~------~
"E
Q)
E
Q)
~
a.
!Jl
'6
0.08
5 10 15
20
25
x
Figure
7.6.
Twenty-five snapshots
oj
the vibrating string from Example 7.4.
We
now consider an example in which one of
the
boundary conditions is in-
homogeneous.
As
usual,
we
use
the
method of shifting
the
data.
Example
7.5.
Consider a string
oj
length 100 cm that has one end fixed at x = 0,
with the other end free to move in the vertical direction only (tied to a frictionless
pole, for example). Let the wave speed in the string
be
c = 2000
cm/
S.45
Suppose the
free end is "flicked," that is, moved up and down rapidly, according to the formula
u(100,
t) =
J(t),
where
f(t)
= {
co-it
-
3c
2
t
2
+
3c
3
t
3
-
c
4
t
4
,
0 < t <
c,
t >
c,
---,------
45The
fundamental
frequency is
then
_c_
=
10Hz.
2
·100
By
comparison,
the
lowest
tone
of a
piano
has
frequency 27.5 Hz.

7.2.
Fourier
series
methods
for the
wave
equation
299
Figure
7.7.
The
"flick"
of
the
free
end in
Example 7.5.
To
determine
the
motion
of
the
string,
we
must
solve
the
IBVP
!!~
c2
^
=o
'
o<x<io(M>o
'
u(ar,0)
=0,
Q<x
<
100,
du
—
(x,0)=0,
0<x<100,
w(0,t)
=
0,
t>0,
u(100,*)
=
/(*),
t>Q.
(7.11)
Since
the
boundary
condition
at the
right
end
of
the
string
is
inhomogeneous,
we
will
shift
the
data
to
obtain
a
problem with homogeneous
boundary
conditions.
Define
v(x,t)
=
u(x,t)
—p(x,t),
where
Then
v
satisfies
the
IBVP
7.2. Fourier
series
methods for the
wave
equation
where E =
0.01
(see Figure 7.7).
0.12..-----....-----...-----,..----~--.....,..--___,
0.1
0.08
c
Q)
E
Q)
al
0.06
a.
({)
15
0.04
0.02
\
0.02 0.04 0.06
t
0.08
0.1
Figure
7.7. The "flick"
of
the free end in Example 7.5.
To
determine the motion
of
the string,
we
must
solve the
IBVP
cPu
2{PU
_ °
ot
2
-
C
ox
2
-
,0
< x < 100, t >
0,
u(x,O) =
0,
0<
x < 100,
ou
ot
(x,
0)
=
0,
0<
x < 100,
u(O,
t)
= 0, t > 0,
u(lOO, t) =
f(t),
t >
0.
0.12
299
(7.11)
Since the boundary condition at the right end
of
the string is inhomogeneous,
we
will
shift the data
to obtain a problem with homogeneous boundary conditions. Define
v(x,
t) =
u(x,
t) -
p(x,
t), where
Then v satisfies the
IB
VP
xf(t)
p(x,
t) =
100'
02v
202v
_ X d
2
f
ot
2
-c
ox
2
-
-100
dt
2
(t),
0<
x < 100, t > 0,
v(x,O) =
0,
0<
x < 100,
OV
x
ot
(x,D) =
-IOOE'
° < X < 100,

300
Chapter
7.
Waves
In
computing
the
initial conditions
for v, we
used
The
new
right-hand side
of the PDE is
Since
g is
defined
piecewise,
so are its
Fourier
coefficients:
The
initial velocity
for v is
given
by
If
we
write
then
the
coefficient
a
n
(t]
is
determined
bv
the
IVP
Again using
the
results
of
Section
4-2.2,
we see
that
300
v(O,
t) = 0, t > 0,
v(100, t) = 0, t >
O.
In computing the initial conditions for v,
we
used
df
1
f(O)
=
0,
-d
(0)
=
-.
t E
The
new right-hand side
of
the PDE is
Chapter 7. Waves
g(x,
t)
=
-1~0
~{
(t)
= {
~
l~O
(-6E-
2
+
18c
3
t -
12c
4
t2)
,
~;:.:::;
E,
Since g is defined piecewise, so
are
its Fourier coefficients:
00
g(x, t) =
I:>n(t)
sin
(mrOx)
,
n=l
10
2
(lOO
(n1fx)
cn(t)
= 10010 g(x,
t)
sin
100 dx
= {
2(~;t
~(t),
0:::;
t
:::;
E,
0,
t > E.
The
initial velocity for v is given
by
x
~
. (n1fx)
-100E
=
~dnsm
100 '
n=l
2
{lOO
(
X)
(n1fx)
d
n
= 100
10
-
100E
sin 100 dx
2(-1)n
If
we
write
00
v(x,
t)
=
~
an(t) sin
(~~~),
then the coefficient an(t) is determined
by
the IVP
~an
c
2
n
2
1f2
dt
2
+ 1002
an
= cn(t),
an(O)
= 0,
~tn(O)
= dn·
Again using the results
of
Section 4.2.2,
we
see
that
100 ( .
(cn1ft)
{t.
(cn1f ) )
an(t)
=
cn1f
d
n
sm
100 +
10
sm
100 (t -
S)
cn(s)
ds
.

while
for t >
e,
Several snapshots
of the
solution
are
shown
in
Figure 7.8.
For
each
t, the
Fourier
coefficients
of
u(x,t]
decay
to
zero relatively slowly
in n, so a
good
approximation
requires
many
terms
in the
Fourier series.
To
produce Figure 7.8,
we
used
200
terms.
The
reader should observe
the
behavior
of the
wave
motion:
the
wave pro-
duced
by the flick of the end
travels from right
to
left,
reflects,
travels from
left
to
right,
reflects
again,
and so on. At
each reflection,
the
wave
inverts.
46
7.2.3
Other
boundary
conditions
Using Fourier series
to
solve
the
wave
equation
with
a
different
set of
boundary
conditions
is not
difficult,
provided
the
eigenvalues
and
eigenfunctions
are
known.
We
now do an
example
with mixed boundary
conditions.
46
The
reader
can
approximate
this
experiment
with
a
long
rope.
7.2.
Fourier
series
methods
for the
wave
equation
301
We
note that
which allows
us to
simplify
the
formulas slightly.
We
will write
Then
we
have
3
7.2.
Fourier
series
methods
for
the
wave
equation
We
note that
,pf
Cn(t)
=
Ed
n
dt
2
(t),
which
allows
us
to
simplify the formulas slightly.
We
will write
Then
we
have
an(t)
=
d;
(Sin
(Ot)
+ E
lot
sin
(O(t
- s))
(-6E-
2
+
18C
3
s -
12C
4
s
2
) dS) .
For
t E
[0,
EJ,
an(t) =
dOn
(Sin
(Ot)
+ E
lot
sin
(O(t
- s))
(-6E-
2
+ 18E-
3
S -
12E-4
S
2)
dS)
= d
n
(.
(()) _ 6
-1
(1
- cos
(Ot)
_ 3
-1
Ot
- sin
((}t)
(}smt
E () E (}2
2 _2(}2t2_2+2COS((}t)))
+ E
~
,
while
for t >
E,
an(t) =
d(}n
(sin
(Ot)
+ E
10'
sin
(O(t
-
S))
(-6E-
2
+
18E-
3
S - 12E-
4
S2)
dS)
_ d
n
(.
(ll) 6
-1
(COS
((}(t
-
E))
-
COS
(Ot)
- - sm
ut
- E
o
()
3
-1
sin
((}(t
-
E))
+
E(}
COS
((}(t
-
S))
- sin
((}t)
E
~
+
301
-2
E
2
02
COS
(O(t
-
E))
- 2 cos
(O(t
-
E))
+
2EO
sin
(O(t
-
E))
+ 2 cos
(Ot)))
2E
(}3 •
Several snapshots of the solution
are
shown in Figure 7.8.
For
each
t, the Fourier
coefficients
of
u(x, t)
decay
to
zero
relatively slowly in n,
so
a
good
approximation
requires
many terms in the Fourier series.
To
produce
Figure 7.8,
we
used
200
terms. The reader should observe the behavior of the
wave
motion: the
wave
pro-
duced
by
the flick
of
the end travels from right
to
left, reflects, travels from left
to
right, reflects
again,
and
so
on.
At
each
reflection, the
wave
inverts.
46
7.2.3 Other boundary conditions
Using Fourier series
to
solve
the
wave equation with a different set of
boundary
conditions is
not
difficult, provided
the
eigenvalues
and
eigenfunctions are known.
We
now do
an
example with mixed
boundary
conditions.
46The
reader
can
approximate
this experiment
with
a long rope.
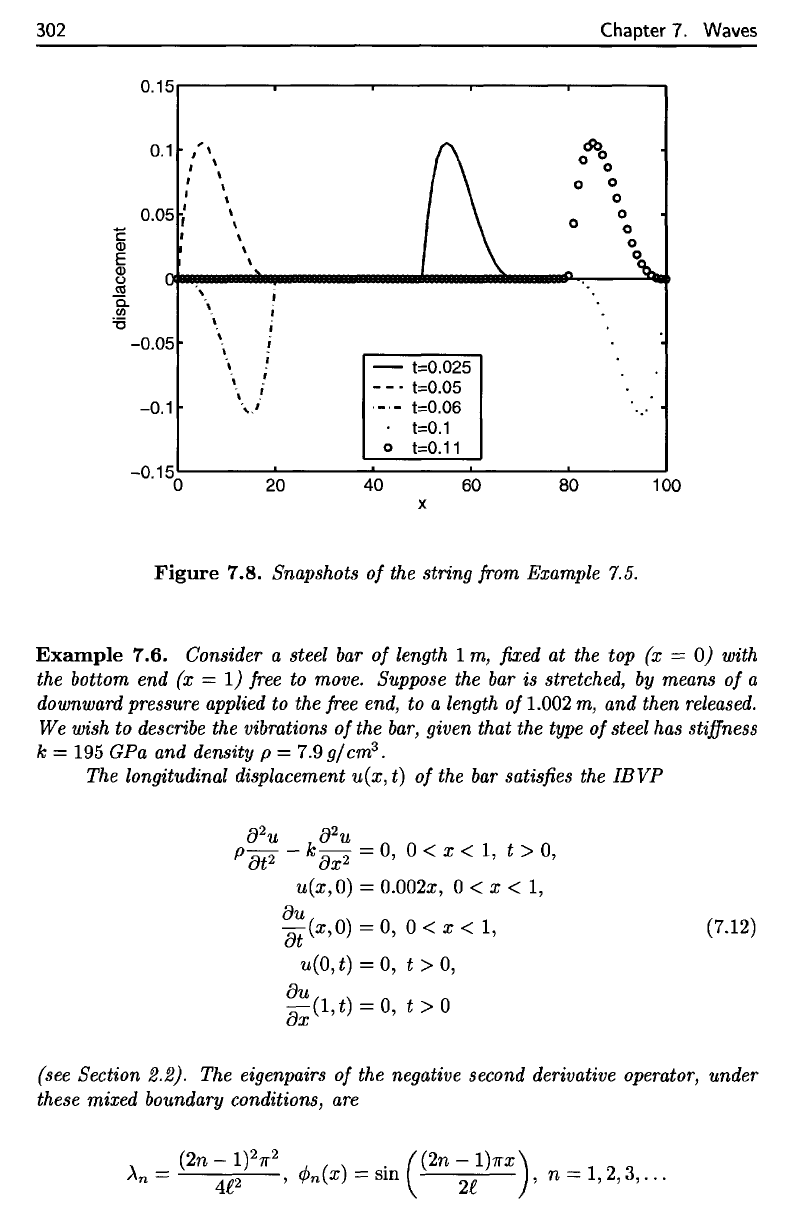
302
Chapter
7.
Waves
Figure
7.8. Snapshots
of
the
string from Example 7.5.
Example
7.6. Consider
a
steel
bar of
length
1
m,
fixed at the top (x —
0)
with
the
bottom
end (x =
I)
free
to
move. Suppose
the bar is
stretched,
by
means
of a
downward
pressure
applied
to the
free
end,
to a
length
of
1.002
m, and
then released.
We
wish
to
describe
the
vibrations
of
the
bar, given that
the
type
of
steel
has
stiffness
k
= 195 GPa and
density
p = 7.9
g/cm
3
.
The
longitudinal displacement
u(x,t)
of the bar
satisfies
the
IBVP
(see
Section 2.2).
The
eigenpairs
of the
negative second derivative operator, under
these mixed boundary conditions,
are
302
c
Q)
E
Q)
u
ttl
C.
C/)
'C
Chapter 7. Waves
0.1
5
O.
1
,',
cSb
o
, \
o 0
,
\
0
\
0
,
\
0
5 '
\
0
,
\
0
0
,
\
0
\
\..
,
0.0
"
,
\
,
\
,
5
\
\
,
-0.0
,
,
-
t=0.025
,
,
;
-
_.
t=0.05
\ ,
-0.
1
',J
,-,-
t=0.06
t=0.1
0
t=0.11
-0.1
5
o 20 40
60
80
100
x
Figure
7.8.
Snapshots
of
the string from Example 7.5.
Example
7.6.
Consider a steel bar
of
length 1 m, fixed
at
the top {x =
O}
with
the bottom end {x = I} free to move. Suppose the bar is stretched, by
means
of
a
downward pressure applied to the free end, to a length
of
1.002 m,
and
then
released.
We wish
to describe the vibrations
of
the bar, given
that
the type
of
steel has stiffness
k
= 195
GPa
and
density p = 7.9
g/
cm
3
•
The longitudinal displacement
u(x,
t)
of
the bar satisfies the
IBVP
fpu
a
2
u
p
at
2
-
k
ax
2
= 0, 0 < x <
1,
t > 0,
u(x,O)
= 0.002x, 0 < x < 1,
au
at
(x,O)
=0,
O<x<l,
u(O, t) = 0, t >
0,
au
ax
(1, t) = 0, t > 0
(7.12)
{see Section
2.2}.
The eigenpairs
of
the negative second derivative operator,
under
these
mixed
boundary conditions, are
(2n -
1)21T2
.
((2n
-
1)1TX)
An
=
4(2
'
tPn(x)
=
sm
2f
' n =
1,2,3,
...

(see
Section 5.2.3), with
1=1.
We
therefore
represent
the
solution
of
(7.12)
as
7.2.
Fourier
series
methods
for the
wave
equation
303
The
left
side
of the PDE is
since
the
right side
is
zero,
we
obtain
the
ODEs
The
initial displacement
is
given
by
with
This, together with
the
fact that
the
initial velocity
of the bar is
zero, yields initial
conditions
for the
ODEs:
The
solution
is
We
see
that
the
wave
speed
in the bar is
(we
convert
k and p to
consistent units
before
computing
c), and the
fundamental
frequency
is
Several
snapshots
of the
displacement
of the bar are
shown
in
Figure 7.9.
7.2. Fourier series methods for
the
wave equation
303
(see Section 5.2.3), with f = 1. We therefore represent the solution
of
(7.12)
as
u(x, t) =
~
an(t) sin
((2n
~
l)7rX).
The left side
of
the
PDE
is
a
2
u a
2
u
~
{J2a
n
k(2n -
1)27r
2
}.
((2n
- l)7rX)
p
at
2
(x,
t) - k ax2 (x, t) =
~
P dt
2
(t) + 4 an(t)
sm
2 ;
since the right side is zero,
we
obtain the ODEs
J2a
n
k(2n -
1)27r
2
P
dt
2
+ 4 an = 0, n =
1,2,3,
....
The initial displacement is given
by
0.002x =
~
b
n
sin
((2n
~
l)7rX),
with
1
1 .
((2n-1)7rX)
2(-1)n+l
b
n
= 2 0.002x
sm
2 dx = (
)2
2'
n =
1,2,3,
....
o 125 2n - 1
7r
This, together with the fact that the initial velocity
of
the
bar
is zero, yields initial
conditions for the ODEs:
d
2
a
n
k(2n -
1)27r
2
P dt
2
+ 4 an = 0,
an(O)
= b
n
,
~tn
(0)
=
O.
The solution is
(
C(2n
-
l)7rt)
an(t) = bncos 2 ' n =
1,2,3,
...
(with c =
Jk/P),
so
( )
~
b (C(2n
-l)7rt)
.
((2n
-l)7rX)
u
x,t
=
L....-
nCOS
sm
.
n=1
2 2
We see that the wave speed in the
bar
is
1.95.10
11
.
7.9.10
3
= 4970
mj
s
(we convert k and p to consistent units before computing c), and the fundamental
frequency is
~
==
49;0
==
1240
Hz.
Several snapshots
of
the displacement
of
the bar
are
shown in Figure 7.9.
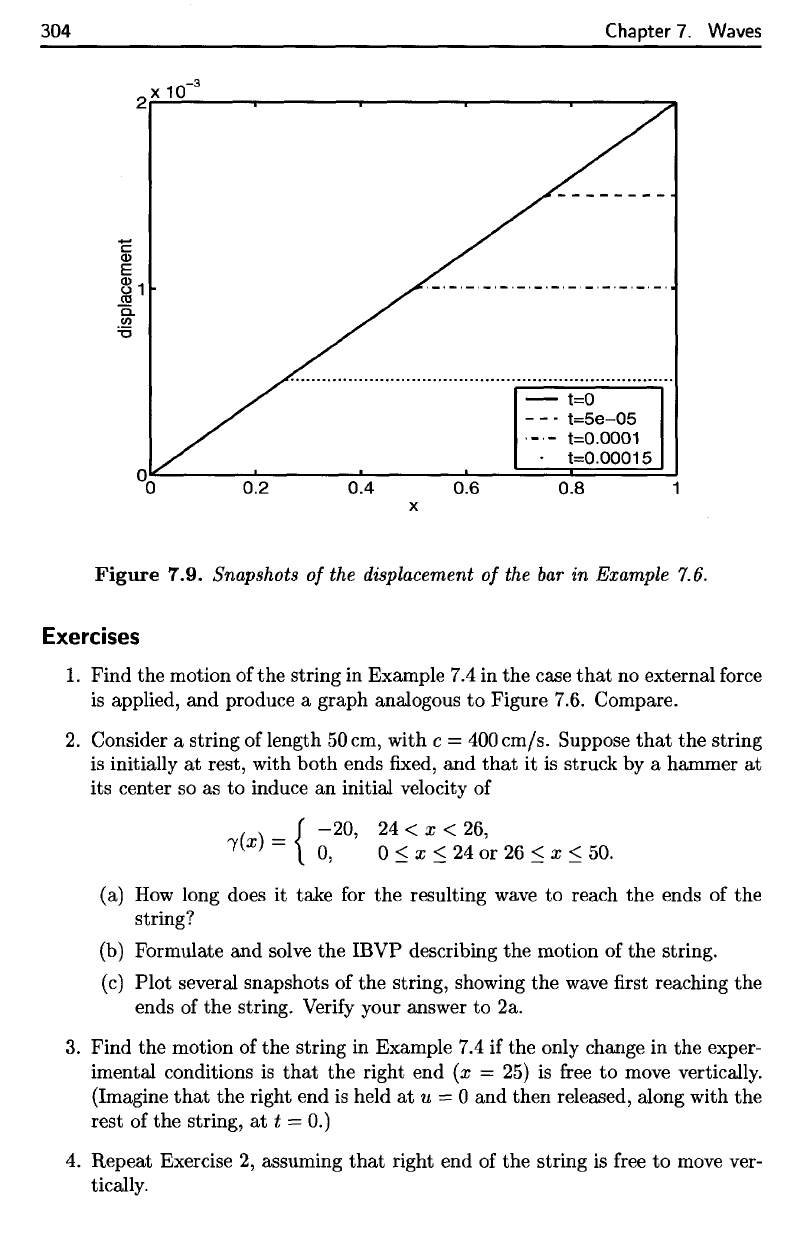
304
Chapter
7.
Waves
Figure
7.9.
Snapshots
of the
displacement
of the bar in
Example
7.6.
Exercises
1.
Find
the
motion
of the
string
in
Example
7.4 in the
case
that
no
external
force
is
applied,
and
produce
a
graph analogous
to
Figure 7.6. Compare.
2.
Consider
a
string
of
length
50 cm,
with
c = 400
cm/s. Suppose
that
the
string
is
initially
at
rest, with both ends
fixed, and
that
it is
struck
by a
hammer
at
its
center
so as to
induce
an
initial velocity
of
(a)
How
long does
it
take
for the
resulting wave
to
reach
the
ends
of the
string?
(b)
Formulate
and
solve
the
IBVP
describing
the
motion
of the
string.
(c)
Plot several snapshots
of the
string, showing
the
wave
first
reaching
the
ends
of the
string.
Verify
your answer
to 2a.
3.
Find
the
motion
of the
string
in
Example
7.4 if the
only change
in the
exper-
imental conditions
is
that
the
right
end (x = 25) is
free
to
move vertically.
(Imagine
that
the
right
end is
held
at u = 0 and
then released, along with
the
rest
of the
string,
at t = 0.)
4.
Repeat Exercise
2,
assuming
that
right
end of the
string
is
free
to
move ver-
tically.
304
"E
Q)
E
~1
0..
Ul
'5
0.2
Chapter 7. Waves
..........................................................................
0.4
0.6
x
-
t=O
-
_.
t=5e-05
._.-
t=0.0001
t=0.00015
0.8
1
Figure
7.9.
Snapshots
of
the displacement
of
the
bar
in
Example 7.6.
Exercises
1.
Find
the
motion
of
the
string in Example 7.4 in
the
case
that
no external force
is applied,
and
produce a
graph
analogous
to
Figure
7.6.
Compare.
2.
Consider a string
of
length 50 cm, with c = 400
cm/s.
Suppose
that
the
string
is initially
at
rest, with
both
ends fixed,
and
that
it
is struck by a
hammer
at
its center so as
to
induce
an
initial velocity
of
{
-20,
24 < x < 26,
"(x)
=
0,
0::;
x
::;
24
or
26
::;
x
::;
50.
(a) How long does
it
take for
the
resulting wave
to
reach
the
ends
of
the
string?
(b) Formulate
and
solve
the
IBVP
describing
the
motion
of
the
string.
(c)
Plot
several snapshots
of
the
string, showing
the
wave first reaching
the
ends of
the
string. Verify your answer
to
2a.
3.
Find
the
motion of
the
string in Example 7.4
if
the
only change in
the
exper-
imental conditions is
that
the
right end
(x
= 25) is free
to
move vertically.
(Imagine
that
the
right end
is
held
at
u = 0
and
then
released, along with
the
rest of
the
string,
at
t = 0.)
4.
Repeat
Exercise
2,
assuming
that
right end of
the
string is free
to
move ver-
tically.

7.3.
Finite
element methods
for the
wave equation
305
5.
Find
the
motion
of the
string
in
Example
7.4 in the
case
that
both ends
of the
string
are
free
to
move vertically. (All other experimental conditions remain
the
same.)
6.
Consider
a
string whose (linear) density
(in the
unstretched
state)
is
0.25
g/cm
and
whose longitudinal
stiffness
is
6500
N
(meaning
that
a
force
of
13pN
is
required
to
stretch
the
string
by
p%).
If the
unstretched (zero tension) length
of
the
string
is 40 cm, to
what
length
must
the
string
be
stretched
in
order
that
its
fundamental
frequency
be
261
Hz
(middle
C)?
7.
How
does
the
motion
of the bar in
Example
7.6
change
if the
force
due to
gravity
is
taken into account?
8.
Consider
a
string
that
has one end fixed,
with
the
other
end
free
to
move
in
the
vertical direction. Suppose
the
string
is put
into motion
by
virtue
of
the
free
end's being manually moved
up and
down periodically.
An
IBVP
describing
this motion
is
Take
t=l,c
=
522,
t
0
= 0, and
e
=
le
- 4.
(a)
Solve
the
IBVP
with
u
not
equal
to a
natural
frequency
of the
string.
Graph
the
motion
of the
string with
uj
equal
to
half
the
fundamental
frequency.
(b)
Solve
the
IBVP with
uj
equal
to a
natural
frequency
of the
string.
Show
that
resonance occurs. Graph
the
motion
of the
string with
u)
equal
to
the
fundamental
frequency.
7.3
Finite
element
methods
for the
wave equation
The
wave equation presents special
difficulties
for the
design
of
numerical methods.
These
difficulties
are
largely caused
by the
fact
that
waves with abrupt changes
(even
singularities, such
as
jump discontinuities)
will
propagate
in
accordance with
the
wave equation, with
no
smoothing
of the
waves.
(Of
course,
if
u(x,t]
has a
singularity,
that
is, it
fails
to be
twice
differentiable,
then
it
cannot
be a
solution
of
the
wave equation unless
we
expand
our
notion
of
what constitutes
a
solution.
But
there
are
mathematically consistent ways
to do
this,
and
they
are
important
for
modeling physical phenomena exhibiting discontinuous behavior.)
7.3. Finite element methods for
the
wave equation
305
5.
Find the motion
ofthe
string in Example 7.4 in
the
case
that
both
ends of the
string are free
to
move vertically. (All other experimental conditions remain
the same.)
6.
Consider a string whose (linear) density (in the unstretched state)
is
0.25
g/cm
and whose longitudinal stiffness
is
6500 N (meaning
that
a force of 13p N
is
required
to
stretch the string by
p%).
If
the
unstretched (zero tension) length
of the string
is
40 cm, to what length must the string be stretched in order
that
its fundamental frequency be
261
Hz (middle C)?
7.
How
does
the
motion of
the
bar in Example
7.6
change if the force due
to
gravity
is
taken into account?
8. Consider a string
that
has one end fixed, with
the
other end free
to
move
in the vertical direction. Suppose the string
is
put
into motion by virtue of
the free end's being manually moved up and down periodically. An IBVP
describing this motion
is
a
2
u a
2
u
at
2
-
c
2
ax
2
=
0,
0 < x < i, t >
to,
u(x,
to)
=
0,
0 < x <
i,
au
at
(x,
to)
=
0,
0 < x < i,
u(O,
t) = 0, t > to,
u(i, t) = E sin
(27TWt)
, t >
to.
Take i =
1,
c = 522,
to
= 0, and E =
Ie
-
4.
(a) Solve the IBVP with w not equal to a natural frequency of the string.
Graph the motion of the string with w equal
to
half the fundamental
frequency.
(b) Solve the IBVP with
w equal
to
a natural frequency of the string. Show
that
resonance occurs. Graph the motion of
the
string with w equal
to
the fundamental frequency.
7.3
Finite element methods
for
the wave equation
The
wave equation presents special difficulties for the design of numerical methods.
These difficulties are largely caused by the fact
that
waves with
abrupt
changes
(even singularities, such as
jump
discontinuities) will propagate in accordance with
the wave equation, with no smoothing of the waves. (Of course, if u(x, t) has a
singularity,
that
is,
it
fails to be twice differentiable, then
it
cannot be a solution
of the wave equation unless
we
expand our notion of what constitutes a solution.
But
there are mathematically consistent ways to do this, and they are important
for modeling physical phenomena exhibiting discontinuous behavior.)

306
Chapter
7.
Waves
For
example,
the
function
if)
:
[0,1]
->
R
defined
by
is
discontinuous.
We
solve both
the
heat
equation,
and
the
wave equation,
with
if)(x}
as the
initial condition
(we
need
a
second initial condition
in the
wave
equation;
we
take
the
initial velocity equal
to
zero).
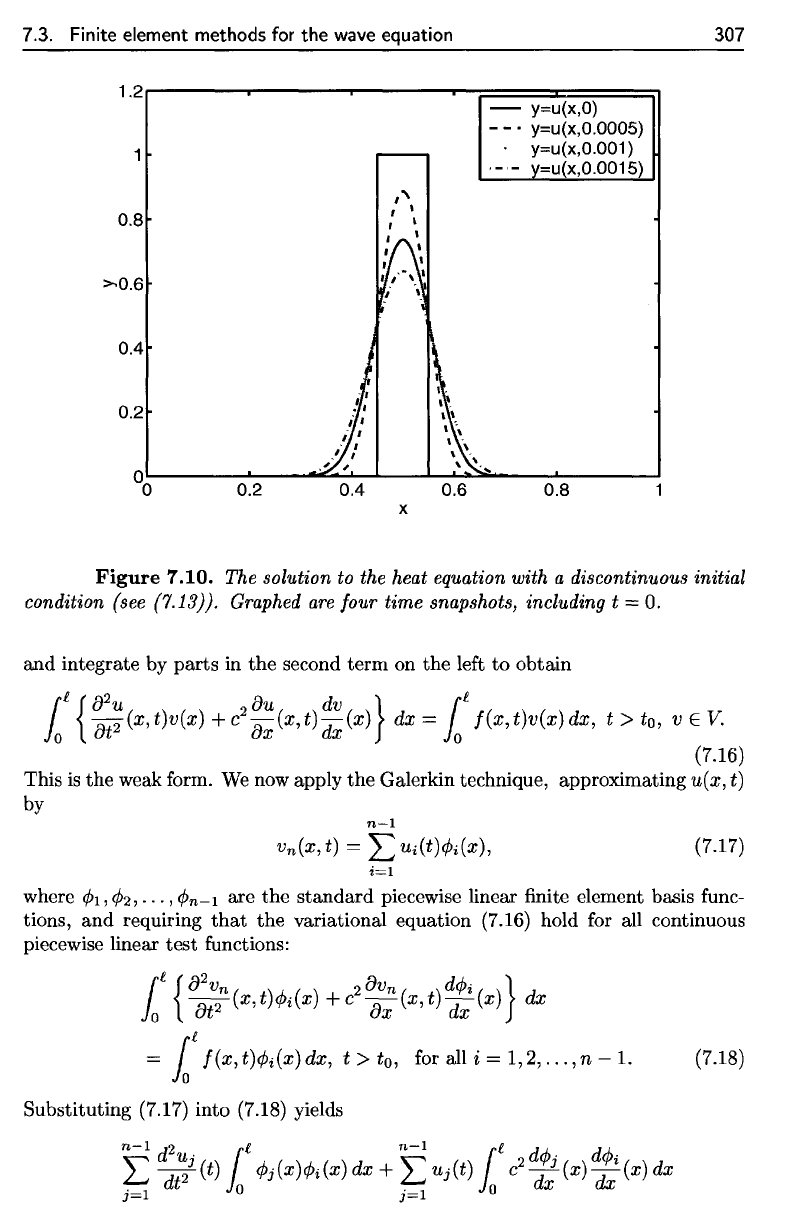
The
results
are
shown
in
Figures
7.10
and
7.11.
The
graphs show
that
the
discontinuity
is
immediately "smoothed
away"
by the
heat
equation,
but
preserved
by the
wave equation.
The
standard
method
for
applying
finite
elements
to the
wave equation, which
we
now
present, works
well
if the
true solution
is
smooth. Methods
that
are
effective
when
the
solution
has
singularities
are
beyond
the
scope
of
this book.
7.3.1
The
wave
equation
with
Dirichlet
conditions
We
proceed
as we did for the
heat equation.
We
suppose
that
u(x,
i)
solves
We
then multiply
the PDE on
both sides
by a
test
function
306
Chapter
7.
Waves
For example,
the
function
'IjJ
:
[0,
1]
-t
R defined by
x _
{I,
Ix
-
~I
< 0.05,
'IjJ(
) - 0,
Ix
-
~I
~
0.05
is discontinuous.
We
solve
both
the
heat
equation,
and
the
wave equation,
au
a
2
u
at
- ax2 = 0, 0 < x < 1, t >
0,
u(x,O) =
'IjJ(x)
,
0<
x <
1,
u(O,t) = 0, t > 0,
u(1, t) = 0, t > 0,
a
2
u a
2
u
at
2
-
ax
2
= 0, ° < x <
1,
t > 0,
u(x,O) =
'IjJ(x),
0<
x <
1,
au
at
(x,
0)
= 0, ° < x <
1,
u(O,
t)
= 0, t >
0,
u(l,
t) = 0, t > 0,
(7.13)
(7.14)
with
'IjJ(x)
as
the
initial condition
(we
need a second initial condition in
the
wave
equation;
we
take
the
initial velocity equal
to
zero).
The
results are shown in Figures
7.10
and
7.11.
The
graphs show
that
the
discontinuity is immediately "smoothed
away" by
the
heat
equation,
but
preserved by
the
wave equation.
The
standard
method for applying finite elements
to
the
wave equation, which
we
now present, works well if
the
true
solution
is
smooth. Methods
that
are effective
when
the
solution has singularities
are
beyond
the
scope of this book.
7.3.1
The
wave equation with Dirichlet conditions
We
proceed as
we
did for
the
heat
equation.
We
suppose
that
u(x, t) solves
a
2
u a
2
u
at
2
-
c
2
ax
2
=
f(x,
t), ° < x <
£,
t >
to,
u(x,
to)
=
'IjJ(x),
0<
x <
£,
au
at
(x,
to)
= l'(x),
0<
x <
£,
(7.15)
u(O,
t) = 0,
t>
to,
u(£,
t) = 0,
t>
to.
We
then
multiply
the
PDE
on
both
sides by a
test
function
v E V = 01[0,£],
7.3.
Finite element methods
for the
wave
equation
307
Figure
7.10.
The
solution
to the
heat equation with
a
discontinuous initial
condition
(see
(7.13)).
Graphed
are
four time snapshots, including
t = 0.
where
</>i,
^
2
,
• •
•,
<$>
n
-\
are the
standard piecewise linear
finite
element basis
func-
tions,
and
requiring
that
the
variational equation (7.16) hold
for all
continuous
piecewise
linear
test
functions:
and
integrate
by
parts
in the
second term
on the
left
to
obtain
This
is the
weak
form.
We now
apply
the
Galerkin
technique, approximating
u(x,
t)
by
Substituting (7.17) into (7.18) yields
7.3. Finite element methods for
the
wave equation
307
1.2
-
y=u(X,O)
-
_.
y=u(x,0.0005)
y=u(x,0.001 )
,-,-
=u(x,0.0015)
"
,
0.8
>-0.6
0.4
0.2
00
0.2 0.4 0.6 0.8
x
Figure
7.10.
The solution to the heat equation with a discontinuous initial
condition
(see
(7.13}). Graphed
are
four time snapshots, including t =
O.
and
integrate by
parts
in
the
second
term
on
the
left
to
obtain
foe
{
~:~
(x, t)v(x) + c
2
~~
(x, t)
~~
(x)}
dx =
foe
f(x,
t)v(x) dx, t >
to,
v E
V.
(7.16)
This is
the
weak form.
We
now apply
the
Galerkin technique, approximating u(x, t)
by
n-l
vn(x, t) = L
Ui(t)CPi(X),
(7.17)
i=l
where
CPl,
CP2,
...
,CPn-l
are
the
standard
piecewise linear finite element basis func-
tions,
and
requiring
that
the
variational equation (7.16) hold for all continuous
piecewise linear
test
functions:
r£
{
{Pv
n
( )
()
2
aV
n
( )
dCPi
(
)}
io
at
2
x, t
CPi
X + c
ax
x, t dx x dx
=
foe
f(x,
t)CPi(X)
dx,
t>
to,
for all i =
1,2,
...
, n - 1. (7.18)
Substituting (7.17) into (7.18) yields
n-l
d
2
u.
r£
n-l
r£
dcp·
dcp'
L
dt2J
(t)
io
CPj
(X)CPi
ex)
dx + L Uj(t)
io
c2-t-ex)
ax'
(x) dx
j=l
0
j=l
0 X
