Gockenbach M.S. Partial Differential Equations. Analytical and Numerical Methods
Подождите немного. Документ загружается.

288
Chapter
7.
Waves
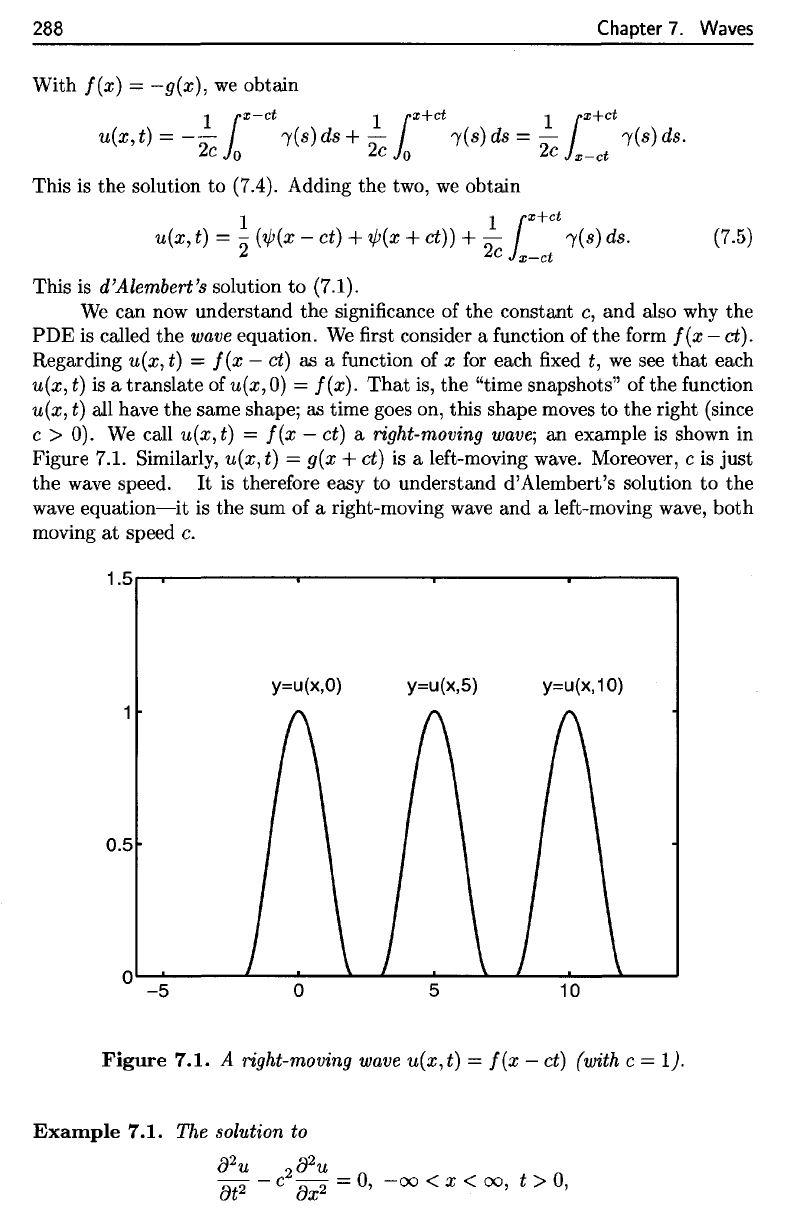
Figure
7.1.
A
right-moving
wave
u(x,t}
=
f(x
—
ct}
(with
c
=
I).
Example
7.1.
The
solution
to
With
/(re)
=
—
g(x},
we
obtain
This
is the
solution
to
(7.4).
Adding
the
two,
we
obtain
This
is
d'Alembert's
solution
to
(7.1).
We
can now
understand
the
significance
of the
constant
c, and
also
why the
PDE is
called
the
wave
equation.
We first
consider
a
function
of the
form
f(x
—
ct}.
Regarding
u(x,
t} =
f(x
—
ct}
as a
function
of x for
each
fixed
t,
we see
that
each
u(x,t)
is a
translate
of
w(x,0)
=
/(#).
That
is, the
"time snapshots"
of the
function
u(x,
t) all
have
the
same shape;
as
time goes
on,
this shape moves
to the
right (since
c > 0). We
call
u(x,t)
=
f(x
—
ct}
a
right-moving
wave]
an
example
is
shown
in
Figure 7.1. Similarly,
u(x,t}
= g(x +
ct}
is a
left-moving wave. Moreover,
c is
just
the
wave speed.
It is
therefore easy
to
understand d'Alembert's solution
to the
wave
equation—it
is the sum of a
right-moving wave
and a
left-moving
wave, both
moving
at
speed
c.
288
Chapter 7. Waves
With
f(x)
=
-g(x),
we
obtain
1 l
x
-
ct
1 l
x
+
ct
1 l
x
+
ct
u(x,
t)
=
--2
')'(8)
d8
+
-2
')'(8)
d8
=
-2
')'(8)
d8.
c 0 C 0 C
x-ct
This is
the
solution
to
(7.4). Adding
the
two,
we
obtain
1 1 l
x
+
ct
u(x, t) =
"2
(¢(x - ct) +
¢(x
+ ct)) +
-2
')'(8)
d8.
c
x-ct
(7.5)
This is d'Alemberl's solution
to
(7.1).
We
can now understand
the
significance of
the
constant c, and also why the
PDE
is called
the
wave
equation.
We
first consider a function of
the
form
f(x
- ct).
Regarding u(x, t) =
f(x
- ct) as a function of x for each fixed t,
we
see
that
each
u(x, t) is a
translate
of u(x, 0) =
f(x).
That
is,
the
"time snapshots" of
the
function
u(x, t) all have
the
same shape; as time goes on, this shape moves
to
the
right (since
c > 0).
We
call u(x, t) =
f(x
- ct) a right-moving
wave;
an
example is shown in
Figure
7.1. Similarly, u(x, t) = g(x + ct) is a left-moving wave. Moreover, c
is
just
the
wave speed.
It
is therefore easy
to
understand d'Alembert's solution
to
the
wave
equation-it
is
the
sum
of
a right-moving wave and a left-moving wave,
both
moving
at
speed
c.
1.Sr--..------..------..------..------,
y=u(x,O) y=u(x,S)
y=u(x,
1
0)
O.S
O~~----~--~--~~--~~~~~--~--~--~
-S
0 S
10
Figure
7.1.
A right-moving
wave
u(x, t) =
f(x
-
ct)
(with c = 1).
Example
7.1.
The
solution
to
E)2u
8
2
u
8t
2
-
c
2
8x
2
= 0,
-00
< x <
00,
t > 0,
7.1.
The
homogeneous wave equation without
boundaries
289
is
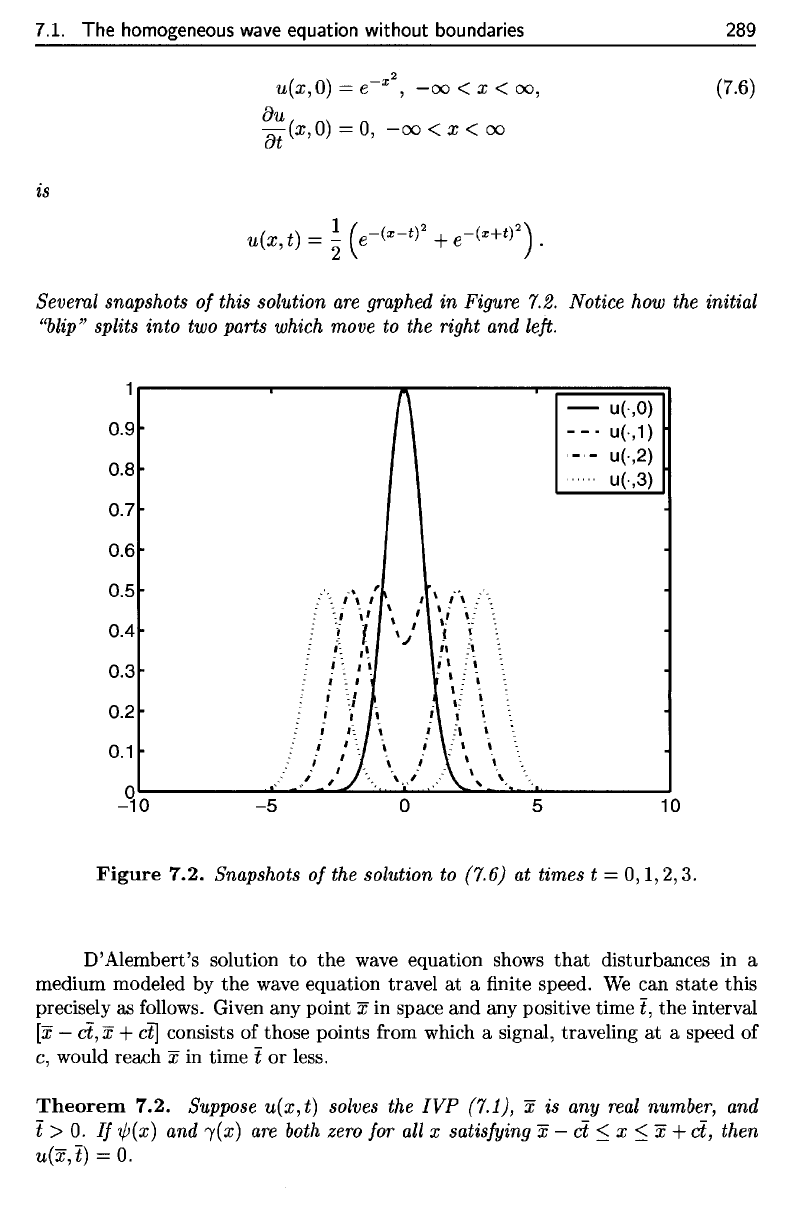
Several
snapshots
of
this solution
are
graphed
in
Figure
7.2. Notice
how the
initial
"blip"
splits
into
two
parts which move
to the
right
and
left.
Figure
7.2. Snapshots
of
the
solution
to
(7.6)
at
times
t =
0,1,2,3.
D'Alembert's solution
to the
wave equation shows
that
disturbances
in a
medium
modeled
by the
wave equation travel
at a finite
speed.
We can
state
this
precisely
as
follows.
Given
any
point
x
in
space
and any
positive time
£,
the
interval
[x
—
ct,x
+
ct\
consists
of
those points
from
which
a
signal, traveling
at a
speed
of
c,
would reach
x in
time
t or
less.
Theorem
7.2.
Suppose
u(x,t)
solves
the
IVP
(7.1),
x is any
real
number,
and
t > 0. //
ifi(x)
and
'j(x)
are
both
zero
for all x
satisfying
x
—
ct
<
x
<
x + ct,
then
u(x,t]
= 0.
7.1.
The
homogeneous wave equation
without
boundaries
289
(
0)
_,,2
U
X,
= e
,-00
< x <
00,
(7.6)
au
at
(x,
0)
= 0,
-00
< x <
00
is
Seveml snapshots
of
this solution
are
gmphed
in
Figure
7.2.
Notice how the initial
"blip" splits into two parts which move to the right and left.
0.9
0.8
0.7
0.6
0.5
0.4
0.3
0.2
0.1
(\
-5
0 5
uLO)
u(·,1 )
u(·,2)
u(·,3)
10
Figure
7.2.
Snapshots
of
the solution to (7.6) at times t =
0,1,2,3.
D'
Alembert's
solution
to
the
wave
equation
shows
that
disturbances
in
a
medium
modeled
by
the
wave
equation
travel
at
a finite speed. We
can
state
this
precisely
as
follows.
Given
any
point
x
in
space
and
any
positive
time
t,
the
interval
[x
-
ct,
x +
ct]
consists
of
those
points
from which a signal,
traveling
at
a
speed
of
c,
would
reach
x
in
time
t
or
less.
Theorem
7.2. Suppose
u(x,
t) solves the
IVP
(7.1), x is any real number, and
t>
o.
If
1jJ(x)
and 'Y(x)
are
both zero for all x satisfying x -
ct
::;
x
::;
X +
ct,
then
u(x, t) =
O.
290
Chapter
7.
Waves
If
tfj(x)
and
7(x)
are
both zero
for all x
satisfying
x
—
ct
<
x
<
x +
ct,
then
all
three
terms
in
this formula
for
u(x,t)
are
zero,
and
hence
u(x,i)
= 0. D
We
therefore call
the
interval
[x
—
ct,x
+
ct\
the
domain
of
dependence
of the
space-time point
(x, t). We
illustrate
the
domain
of
dependence
in
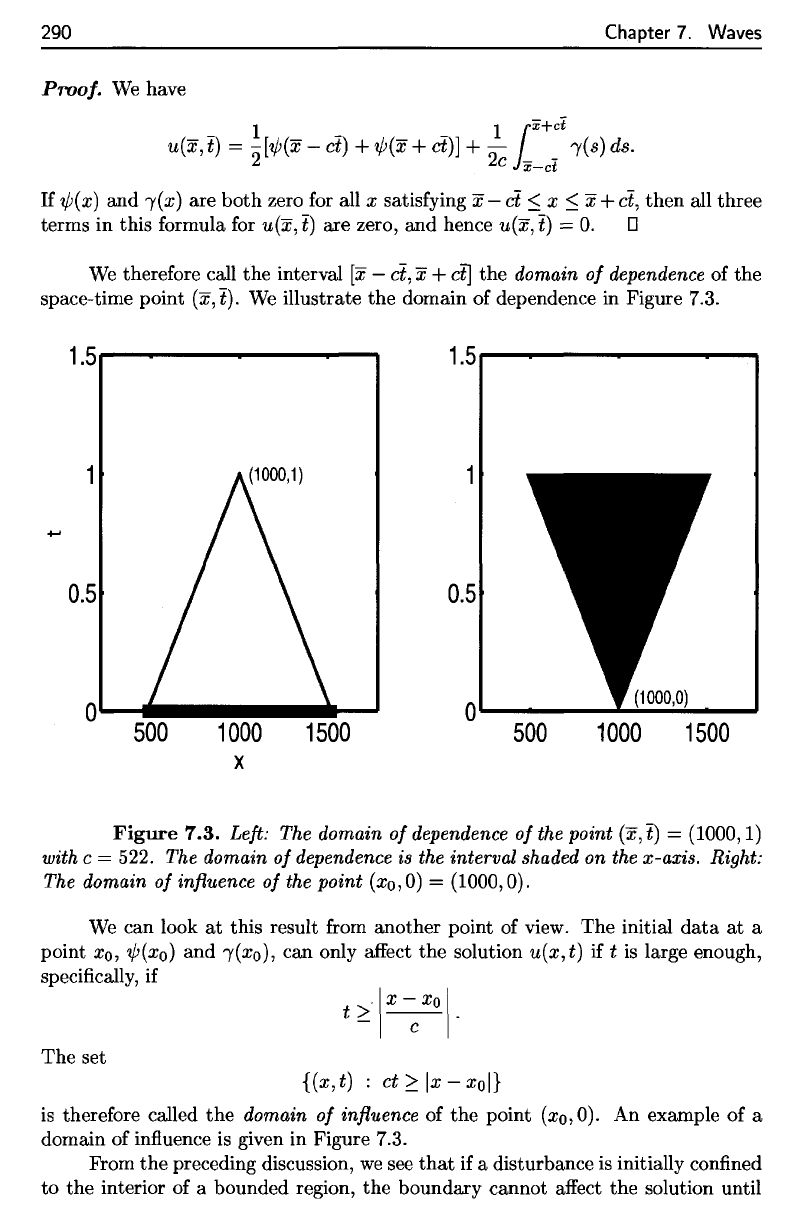
Figure 7.3.
is
therefore called
the
domain
of
influence
of the
point
(xo,0).
An
example
of a
domain
of
influence
is
given
in
Figure 7.3.
From
the
preceding discussion,
we see
that
if a
disturbance
is
initially
confined
to the
interior
of a
bounded region,
the
boundary cannot
affect
the
solution until
Figure
7.3.
Left:
The
domain
of
dependence
of
the
point
(x, t) =
(1000,1)
with
c =
522.
The
domain
of
dependence
is the
interval
shaded
on the
x-axis. Right:
The
domain
of
influence
of the
point
(#o,0)
=
(1000,0).
We
can
look
at
this result
from
another point
of
view.
The
initial
data
at a
point
#o,
VK
x
o)
and
7(^0),
can
only
affect
the
solution
u(x,t)
if t is
large enough,
specifically,
if
The set
Proof.
We
have
290 Chapter 7. Waves
Proof.
We
have
- 1 - - 1 l
x
+
d
u(1',
t) = 2
['IjJ(1'
- ct) +
'IjJ(1'
+ ct)] + 2 _ _
')'(s)
ds.
c
x-ct
If
'IjJ(x)
and
')'(x) are
both
zero for all x satisfying
1'-
d
:::;
x
:::;
1'+
d,
then
all
three
terms
in
this formula for
u(1',
t) are zero,
and
hence
u(1',
t) =
0.
0
We
therefore call
the
interval
[x
- d, x + d]
the
domain
of
dependence
of
the
space-time point (x, t).
We
illustrate
the
domain
of
dependence in Figure 7.3.
1.5,----------.,
1.5,---------~
1
0.5 0.5
OL.......:_-
...
--=-.....J
O~------~~~--~
500
1000
1500
500
1000
1500
X
Figure
7.3.
Left: The domain
of
dependence
of
the point (x, t) = (1000,1)
with c = 522. The domain
of
dependence is the interval shaded on the x-axis. Right:
The domain
of
influence
of
the point (xo,O) = (1000,0).
We
can look
at
this result from
another
point of view.
The
initial
data
at
a
point
xo,
'IjJ(xo)
and
')'(xo), can only affect
the
solution u(x, t) if t is large enough,
specifically,
if
t
~
\x
~
Xo
\.
The
set
{(x,
t)
: ct
~
Ix - xol}
is
therefore called
the
domain
of
influence
of
the
point (xo,O).
An
example
of
a
domain
of
influence is given in Figure 7.3.
From
the
preceding discussion,
we
see
that
if
a disturbance is initially confined
to
the
interior
of
a bounded region,
the
boundary
cannot affect
the
solution until

7.2.
Fourier
series
methods
for the
wave
equation
291
sufficient
time
has
passed.
For
this reason,
the
solution
to the
wave equation
in an
infinite
medium provides
a
realistic
idea
of
what happens
(in
certain
experiments)
in
a
bounded region,
at
least
for a finite
period
of
time (namely, until enough
time
has
elapsed
for the
disturbance
to
reach
the
boundary). However, there
is no
simple
formula
for the
solution
of the
wave equation subject
to
boundary conditions.
To
attack
that
problem,
we
must
use
Fourier series,
finite
elements,
or
other less
elementary methods.
Exercises
1.
Solve (7.1) with
7(0;)
= 0 and c —
522.
43
Graph several snapshots
of the
solutions
on a
common
plot.
2.
Solve (7.1) with
ip(x)
= 0,
and c =
522. Graph several snapshots
of the
solutions
on a
common plot.
3.
Consider
the
IVP
(7.1) with
j(x)
= 0 and
The
initial displacement consists
of two
"blips," which, according
to
d'Alembert's
formula,
will
each split into
a
right-moving
and a
left-moving wave. What
happens
when
the
right-moving wave
from
the first
blip meets
the
left-moving
wave
from
the
second blip?
4.
Repeat
the
previous exercise with
7.2
Fourier
series
methods
for the
wave
equation
Fourier
series methods
for the
wave equation
are
developed just
as for the
heat
equation—the
key is to
represent
the
solution
in a
Fourier series
in
which
the
Fourier
coefficients
are
functions
of t. We
begin with
the
IBVP
43
The
value
522 is
physically meaningful,
as we
will
see in the
next section.
7.2. Fourier
series
methods for the
wave
equation
291
sufficient time
has
passed. For this reason,
the
solution
to
the
wave
equation
in
an
infinite
medium
provides a realistic
idea
of
what
happens
(in
certain
experiments)
in a
bounded
region,
at
least for a finite period
of
time
(namely, until enough
time
has elapsed for
the
disturbance
to
reach
the
boundary).
However,
there
is
no
simple formula for
the
solution
of
the
wave
equation
subject
to
boundary
conditions.
To
attack
that
problem, we
must
use Fourier series, finite elements,
or
other
less
elementary methods.
Exercises
1.
Solve (7.1)
with
,,(x) = {
0,
x <
-2
or
x >
2,
5·
1Q-4
x
+
10-
3
,
-2
:s;
x
:s;
0,
-5·
1Q-4
x
+
10-
3
,
0 < X
:s;
2,
,(x)
= 0
and
c =
522.43
Graph
several snapshots of
the
solutions on a
common plot.
2.
Solve (7.1)
with
'IjJ(x)
= 0,
,(x)
= {
0,
-1,
x <
-0.5
or x > 0.5,
Ixl
:s;
0.5,
and
c = 522.
Graph
several snapshots
of
the
solutions
on
a common plot.
3. Consider
the
IVP
(7.1)
with
,(x)
= 0
and
The
initial displacement consists of two "blips," which, according
to
d'
Alembert 's
formula, will each split
into
a right-moving
and
a left-moving wave.
What
happens
when
the
right-moving wave from
the
first blip meets
the
left-moving
wave from
the
second blip?
4.
Repeat
the
previous exercise
with
7.2 Fourier series methods for the wave equation
Fourier series
methods
for
the
wave
equation
are
developed
just
as for
the
heat
equation-the
key is
to
represent
the
solution in a Fourier series in which
the
Fourier
coefficients
are
functions
of
t. We begin
with
the
IBVP
a
2
u a
2
u
at
2
-
c
2
ax
2
=
f(x,
t), 0 < x <
£,
t >
to,
43The value 522 is physically meaningful,
as
we will see
in
the
next
section.

where
Using
the
same reasoning
as in
Section
6.1,
we can
express
the
left-hand side
of the
PDE in a
sine series:
292
Chapter
7.
Waves
which
models
the
small displacements
of a
vibrating string.
We
write
the
solution
in
the
form
where
We
also expand
the
right-hand side
/(#,£)
in a
sine
series
Setting
this
equal
to the
series
for
/(#,£),
we
obtain
the
ODEs
Initial conditions
for
these ODEs
are
obtained
from
the
initial conditions
for the
wave
eauation
in
(7.7).
If
then
we
have
We
thus
find the
Fourier sine
coefficients
of the
solution
u(x,
t)
by
solving
the
IVPs
292
Chapter
7. Waves
u(x, to) =
1/J(x)
, ° < x <
e,
au
at
(x, to) = 1'(x), ° < x <
e,
(7.7)
u(O,
t) = 0, t > to,
u(e,t)
= 0,
t>
to,
which models the small displacements of a vibrating string.
We
write the solution
in the form
~
.
(n7fx)
u(x,
t) =
~
an(t) sm
-e-
,
n=l
where
an(t) =
~
1i
u(x, t) sin
(n;x)
dx, n =
1,2,3,
....
We
also expand the right-hand side
f(x,
t) in a sine series:
00
f(x,t)
=
LCn(t)
sin
(n;x),
n=l
where
Cn(t)
=
~
1i
f(x,
t) sin
(n;x)
dx, n =
1,2,3,
....
Using
the
same reasoning as in Section 6.1,
we
can express the left-hand side of the
PDE
in a sine series:
a
2
u a
2
u
00
(d2a
c
2
n
2
7f2 )
(n7fx)
at
2
(x, t) -
c
ax
2
(x, t)
=
~
dt
2n
(t) +
~an(t)
sin
-e-
.
Setting this equal to the series for
f(x,
t),
we
obtain
the
ODEs
~an
2n
2
7f2
dt
2
+
-e-2-an
= cn(t), n =
1,2,3,
....
Initial conditions for these ODEs are obtained from the initial conditions for the
wave equation in (7.7).
If
~
.
(n7fx)
~.
(n7fx)
1/J(x)
=
~
b
n
sm
-e-
, 1'(x) =
~
d
n
sm
-e-
,
n=l
n=l
then
we
have
)
dan
an(to = b
n
, dt
(to)
= d
n
.
We
thus find the Fourier sine coefficients of the solution u(x, t) by solving the IVPs
~an
c
2
n
2
7f2
dt
2
+
-e-2-an
= cn(t),
an(to)
= b
n
,
dan
( )
--;It
to
=d
n
,
(7.8)

in
which
case
the
units
can be
thought
of as
radians/seconds.
7.2.
Fourier
series
methods
for the
wave
equation
293
for
n
=
1,2,3,
— In
Section 4.2.2,
we
presented
an
explicit formula
for
the
solution
of
(7.8).
The use of
this formula
is
illustrated
in
Example
7.4
below.
7.2.1 Fourier
series
solutions
of the
homogeneous
wave
equation
When
the
wave
equation
is
homogeneous
(that
is,
when
/
=
0), the
Fourier series
solution
is
especially instructive.
We
then must solve
is
44
The
units
of
frequency
are
literally I/second,
which
is
interpreted
as
cycles
per
second,
or
Hertz.
Sometimes
the
natural
frequencies
are
given
as
The
frequencies
en/
(21}
are
called
the
natural
frequencies
of the
string.
44
These fre-
quencies
are
called
natural
because
any
solution
of the
homogeneous wave equation
is
an
(infinite)
combination
of the
normal
modes
of the
string,
This formula shows
the
essentially oscillatory nature
of
solutions
to the
wave equa-
tion; indeed,
the
Fourier sine coefficients
of the
solution
are
periodic:
Therefore,
the
solution
to
which
yields
7.2. Fourier
series
methods for the
wave
equation
293
for n =
1,2,3,
....
In
Section 4.2.2,
we
presented
an
explicit formula for
the
solution
of (7.8).
The
use of this formula
is
illustrated in Example 7.4 below.
7.2.1 Fourier
series
solutions
of
the homogeneous wave equation
When the wave equation
is
homogeneous
(that
is, when f
==
0),
the
Fourier series
solution
is
especially instructive.
We
then must solve
tPa
n
r?n
2
7f2
dt
2
+~an=O,
an(to) = b
n
,
dan ( )
dt
to
= dn,
which yields
Therefore, the solution to
a
2
u a
2
u
at
2
-
c
2
ax
2
= 0, 0 < x <
i,
t > to,
u(x,
to) =
'IjJ(x)
, 0 < x <
i,
au
at
(x, to) = 'Y(x), 0 < x <
i,
u(O,
t) = 0, t > to,
u(i,
t) = 0, t > to,
is
)
~{
(m7f( )
dni.
(m7f
)}.
(n7fx)
u(x,t
=
~
bncos
-i-
t-to)
+
m7f
sm
--yet-to)
sm
-f-
.
(7.9)
This formula shows
the
essentially oscillatory
nature
of solutions to
the
wave equa-
tion; indeed, the Fourier sine coefficients of the solution are periodic:
an
(t
+
~!)
= an(t) for all t.
The frequencies
cn!
(2l) are called
the
natural frequencies of the string.44 These fre-
quencies are called
natural
because any solution
of
the homogeneous wave equation
is
an
(infinite) combination of
the
normal modes of the string,
(
(
cn7f
) . (cn7f
))
.
(n7fx)
____
--'A_n
cos
-f.-
(t -
to)
+
Bn
sm
-f.-
(t
-
to)
sm
-f.-
.
44The
units
of frequency
are
literally
l/second,
which is
interpreted
as cycles
per
second,
or
Hertz. Sometimes
the
natural
frequencies are given as
cn
cn7l'
271'-=-
2£
£'
in which case
the
units
can
be
thought
of as radians/seconds.
294
Chapter
7.
Waves
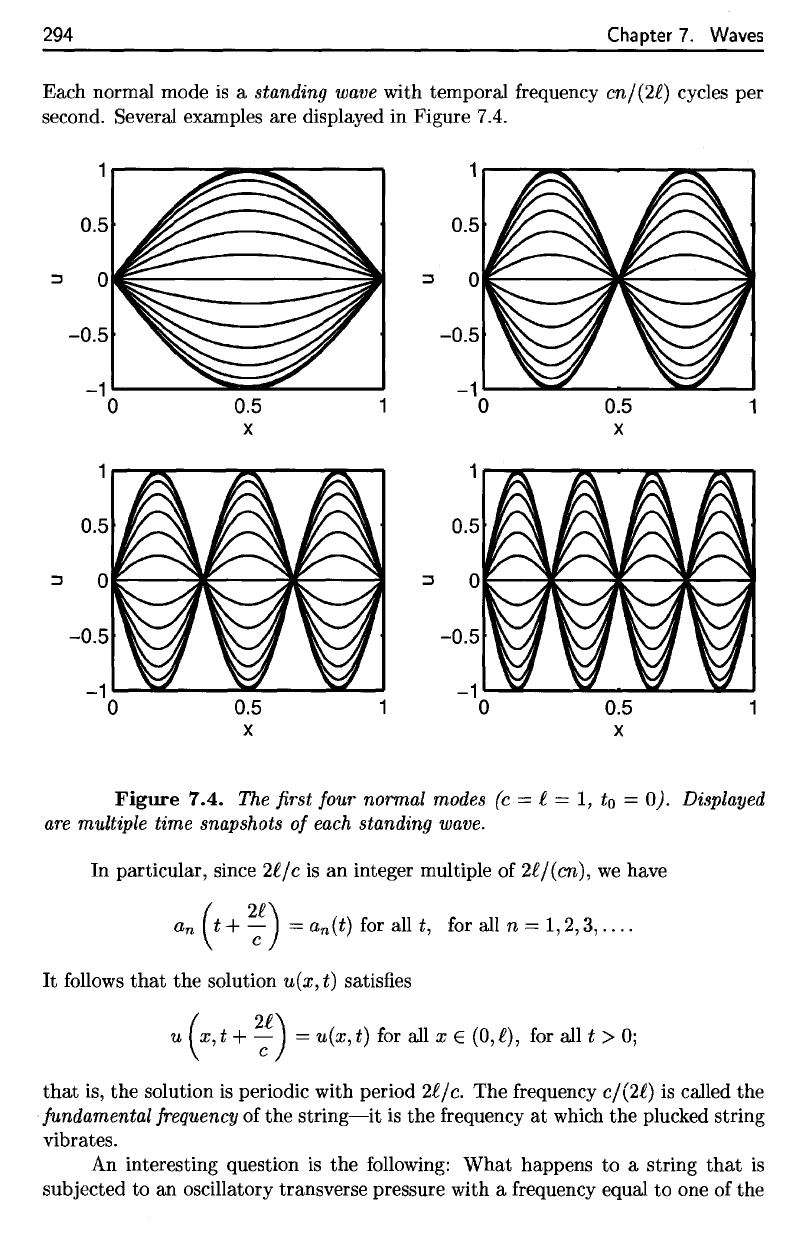
Each normal mode
is a
standing
wave
with temporal
frequency
en/
(21)
cycles
per
second. Several examples
are
displayed
in
Figure 7.4.
that
is, the
solution
is
periodic with period
2£/c.
The
frequency
c/(2l)
is
called
the
fundamental
frequency
of the
string—it
is the
frequency
at
which
the
plucked string
vibrates.
An
interesting question
is the
following:
What
happens
to a
string
that
is
subjected
to an
oscillatory transverse pressure with
a
frequency
equal
to one of the
Figure
7.4.
The first
four normal
modes
(c =
I
=
1,
to = 0).
Displayed
are
multiple time snapshots
of
each
standing wave.
In
particular, since
2t/c
is an
integer multiple
of
2^/(cn),
we
have
It
follows
that
the
solution
u(x,t)
satisfies
294 Chapter
7.
Waves
Each normal mode
is
a standing
wave
with temporal frequency cn/(2£) cycles per
second. Several examples are displayed in Figure 7.4.
0.5
-0.5
-1L-----~~~----~
a
0.5
x
-1~--~----~------~~
a
0.5
x
0.5
:::J
O~---____::.:----__:JI
-0.5
-1~--~~------~&---~
a
0.5
-0.5
0.5
x
1
-1~~----~--~----~
a
0.5
x
1
Figure
7.4.
The
first four normal modes
(c
= f = 1,
to
= 0). Displayed
are
multiple time snapshots
of
each
standing
wave.
In particular, since 2£/c
is
an integer multiple of 2£/(cn),
we
have
an
(t
+
2c
f
)
= an(t) for all
t,
for all n =
1,2,3,
....
It
follows
that
the solution u(x, t) satisfies
u
(x,
t +
2c
f
)
= u(x, t) for all x E (0,
f),
for all t >
0;
that
is,
the
solution
is
periodic with period 2f/c. The frequency c/(2£)
is
called
the
fundamental frequency of the
string-it
is
the frequency
at
which the plucked string
vibrates.
An interesting question
is
the following:
What
happens
to
a string
that
is
subjected to an oscillatory transverse pressure with a frequency equal
to
one of
the

7.2.
Fourier
series
methods
for the
wave
equation
295
natural
frequencies
of the
string?
The
answer
is
that
resonance occurs. This
is
illustrated
in
Exercise
8 and
also
in
Section 7.4.
We
now
give
an
example
of
using
the
Fourier series method
to
solve
an
IBVP
for
the
wave
equation.
Example
7.3. Consider (7.7) with
1=1,
c =
522,
f(x,t)
=
0,
7(0;)
= 0, and
The
fundamental
frequency
of the
string
is
then
which
is the
frequency
of
the
musical note
called
"middle
C."
The
initial conditions
indicate
that
the
string
is
"plucked"
at the
center.
Using
the
notation
introduced
above,
we
have
c
n
(t]
= 0 and
d
n
= 0 for all n, and
We
must solve
The
solution
is
easily
seen
to be
and
therefore
Several
snapshots
of the
solution
are
graphed
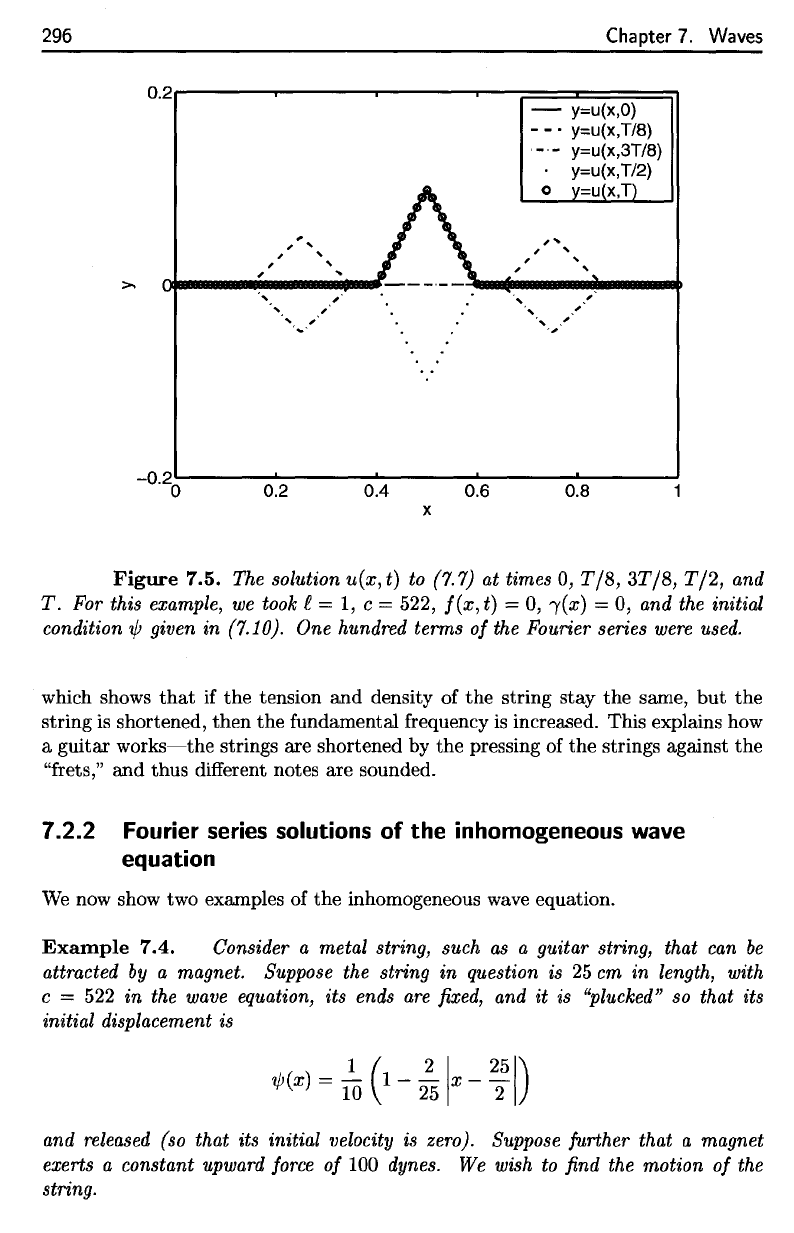
in
Figure 7.5.
The
reader
should
observe
that when
a
wave hits
a
boundary
where there
is a
Dirichlet condition,
the
wave inverts
and
reflects.
Therefore,
for
example,
w(x,3T/8)
=
—u(x,T/8]
and
u(x,T/2)
=
—u(x,ty,
where
T is the
period
corresponding
to the
fundamental
frequency:
T —
2/522
=
1/261.
Also,
u(x,T)
=
w(x,0),
as
expected.
The
reader should recall,
from
Section 2.3,
that
the
wave speed
c is
determined
by
the
tension
T and the
density
p of the
string:
c
2
=
T/p.
The
fundamental
frequency
of the
string
is
7.2. Fourier series methods for the
wave
equation
295
natural frequencies of the string? The answer
is
that
resonance occurs. This
is
illustrated in Exercise 8 and also in Section 7 A.
We
now give
an
example of using
the
Fourier series method
to
solve an
IBVP
for the wave equation.
Example
7.3. Consider (7.7) with £ = 1, c = 522,
f(x,
t) = 0, 'Y(x) = 0, and
{
X -
004,
004
< x < 0.5,
'IjJ(x)
=
-(x
- 0.6), 0.5 < x < 0.6, (7.10)
0,
0 < x <
004
or 0.6 < x <
1.
The fundamental frequency
of
the string is then
C
522
- = -
=261
Hz
2£
2 '
which is the frequency
of
the musical note called "middle C." The initial conditions
indicate that the string is ''plucked'' at the center. Using the notation introduced
above,
we
have cn(t) = 0 and d
n
= 0 for all
n,
and
b
n
= 2
101
'IjJ(x)
sin (mfx) dx
=
-2 -2
sin(I/2mf)
+ sin(2/5mf) +
sin(3/5mf).
n
2
7f2
We
must
solve
~an
2 2 2
dt
2
+ c n 7f an =
0,
an(O)
= b
n
,
d:
tn
(0)
=
O.
The solution is easily seen to
be
an(t) = b
n
cos(cn7ft), n =
1,2,3,
...
,
and therefore
00
u(x,t)
=
L:)n
cos
(cn7ft)
sin (n7fx).
n=l
Several snapshots
of
the solution
are
graphed
in
Figure
7.5.
The reader should
observe that when a wave hits a boundary where there is a Dirichlet condition,
the wave inverts and reflects. Therefore, for example,
u(x,
3T
/8) =
-u(x,
T /8)
and
u(x,
T /2) =
-u(x,O),
where T is the period corresponding to the fundamental
frequency: T = 2/522 = 1/261. Also,
u(x,
T)
=
u(x,
0),
as
expected.
The reader should recall, from Section 2.3,
that
the
wave speed c
is
determined
by
the
tension T and the density p of the string: c
2
= T /
p.
The fundamental
frequency of the string
is
296
Chapter
7.
Waves
which
shows
that
if the
tension
and
density
of the
string stay
the
same,
but the
string
is
shortened,
then
the
fundamental frequency
is
increased.
This
explains
how
a
guitar
works—the
strings
are
shortened
by the
pressing
of the
strings against
the
"frets,"
and
thus
different notes
are
sounded.
7.2.2
Fourier
series
solutions
of the
inhomogeneous
wave
equation
We
now
show
two
examples
of the
inhomogeneous wave equation.
Example
7.4. Consider
a
metal string, such
as a
guitar string, that
can be
attracted
by a
magnet.
Suppose
the
string
in
question
is 25 cm in
length, with
c = 522 in the
wave
equation,
its
ends
are fixed, and it is
"plucked"
so
that
its
initial displacement
is
and
released
(so
that
its
initial velocity
is
zero).
Suppose
further that
a
magnet
exerts
a
constant
upward
force
of 100
dynes.
We
wish
to find the
motion
of the
string.
Figure
7.5.
The
solution
u(x,t)
to
(7.7)
at
times
0,
T/8, 3T/8, T/2,
and
T.
For
this example,
we
took
I
= 1, c =
522,
/(#,£)
=
0,
7(2)
=
0,
and the
initial
condition
ijj
given
in
(7.10).
One
hundred
terms
of the
Fourier series
were
used.
296
Chapter 7. Waves
0.2r------.-----r-------.---;:=======il
- y=u(x,O)
,.
, ,
, ,
, ,
,
,
-
-'
y=u(x,T/8)
y=u(x,3T/8)
y=u(x,T/2)
o
=U
x,T
,
...
, ,
, ,
, ,
-0.2'-----
.......
---'-----'-----.&...-----'
o 0.2 0.4 0.6 0.8
x
Figure
7.5. The solution
u(x,t)
to
{7.7}
at times 0, T18, 3T18, T12, and
T.
For this example,
we
took £ = 1, c = 522,
f(x,t)
= 0, "((x) = 0, and the initial
condition'IjJ given in (7.10). One hundred terms
of
the Fourier series were used.
which shows
that
if the tension and density of
the
string stay
the
same,
but
the
string
is
shortened,
then
the fundamental frequency is increased. This explains how
a guitar
works-the
strings are shortened by the pressing of the strings against the
"frets," and thus different notes are sounded.
7.2.2 Fourier
series
solutions of the inhomogeneous wave
equation
We
now show two examples of the inhomogeneous wave equation.
Example
7.4.
Consider a metal string, such
as
a guitar string, that can
be
attracted
by
a magnet. Suppose the string in question is
25
cm in length, with
c
= 522 in the wave equation, its ends
are
fixed, and
it
is "plucked" so that its
initial displacement is
'I/J(x)
=
~
(1
-
~
Ix
_
25
1)
10
25
2
and released (so that its initial velocity
is zero). Suppose further that a magnet
exerts a constant upward force
of
100 dynes. We wish to find the motion
of
the
string.

7.2. Fourier series
methods
for the
wave
equation
297
We
must solve
the
IBVP
where
c — 522 and
^
is
given
above.
We
write
the
solution
as
and
determine
the
coefficients
ai
(£),
02
(£),
03
(£),...
by
solving
the
IVPs
(7.8).
We
have
with
and
with
To
find
a
n
(t],
therefore,
we
must solve
Using
the
results
of
Section
4-2.2,
we see
that
the
solution
is
7.2. Fourier
series
methods for the
wave
equation 297
We
must
solve
the
IBVP
cPu
a
2
u
at
2
-
c
2
ax
2
= 100, ° < x < 25, t > 0,
u(x, 0) =
1jJ(x),
° < x < 25,
au
at
(x, 0) = 0, ° < x < 25,
u(O,
t)
= 0, t > 0,
u(25,
t)
= 0, t > 0,
where
c = 522 and
1jJ
is
given
above.
We
write the solution
as
00
u(x, t) = L an(t) sin
(n;x)
n=l
and determine the coefficients al(t),a2(t),a3(t),
...
by
solving the IVPs
{7.8}.
We
have
00
100 = L
cnsin
(n;x),
n=l
with
2
[25
.
(n7fx)
200(1-
(_l)n)
C
n
= 25
10
100
sm
25
dx =
n7f
' n =
1,2,3,
...
,
and
with
b
=
~
[25
",.(
) .
(n7fx)
d = 4 sin (n7f/2)
n 25
10
'f/
X
sm
25 x
5n
2
7f2
, n =
1,2,3,
....
To
find an(t), therefore,
we
must
solve
d
2
a
n
c
2
n
2
7f2
dt
2
+
~an
=
Cn,
an(O) = b
n
,
d;t
n
(0) = 0.
Using
the results of Section 4.2.2,
we
see
that the solution
is
