Gockenbach M.S. Partial Differential Equations. Analytical and Numerical Methods
Подождите немного. Документ загружается.


258
Chapter
6.
Heat flow
and
diffusion
Substituting (6.39) into
(6.40)
yields,
for t > to and
i
=
1,2,
...,n
—
1,
If
we now
define
the
mass matrix matrix
M and the
stiffness
matrix
K by
Mij
= I
pc(f)j(x)(f)i(x}dx,
Kij
= I
K—^-(x)^
±
(x)dx,
Jo
Jo
dx
dx
and the
vector-valued
functions
f
(t}
and
a(t)
by
Galerkin's
method leads
to
or
then
we can
write (6.41)
as
(The names "mass matrix"
and
"stiffness
matrix"
for M and K,
respectively, arise
from
the
interpretation
for
similar matrices appearing
in
mechanical models.
We
have
already seen
the
stiffness
matrix
in
Chapter
5; we
will
see the
mass matrix
in
Chapter
7. In the
context
of the
heat equation, these names
are not
particularly
meaningful,
but the
usage
is
well established.)
The
initial condition
u(x,to)
=
ip(x),
0 < x < t can be
approximately imple-
mented
as
258
Chapter
6.
Heat flow
and
diffusion
Galerkin's method leads to
10£
{PC
a;t
n
(x, t)v(x) +
'"
~:n
(x, t)
~~
(X)} dx
=
10£
!(x,
t)v(x) dx for all v E Sn,
t>
to,
or
i
f {
aU
n
( )
()
aU
n
( )
dcPi
) }
o
pC7it
x, t
cPi
X +
'"
ax
x, t dx (x dx
=
Ioi
!(x,
t)
cPi
(x) dx, t >
to,
i = 1,2,
...
, n
-1.(6.40)
Substituting (6.39) into (6.40) yields, for t >
to
and i = 1,2,
...
, n -
1,
If
we
now define the mass matrix matrix M and the stiffness matrix K by
r
i
r
f
dcP'
dcPi
Mij =
10
pecPj
(X)cPi(X)
dx, Kij =
10
'"
a::
(x) dx (x) dx,
and
the
vector-valued functions
f(t)
and
a(t) by
f(t)
=
then
we
can write (6.41) as
da
M dt +
Ka
= f(t).
(The names "mass matrix" and "stiffness matrix" for M and
K,
respectively, arise
from
the
interpretation for similar matrices appearing in mechanical models.
We
have already seen the stiffness matrix in Chapter
5;
we
will see the mass matrix in
Chapter
7.
In the context of the heat equation, these names are not particularly
meaningful,
but
the
usage is
well
established.)
The initial condition
u(x,
to)
=
'I/J(x),
0 < x < l can be approximately imple-
mented as
n-l n-l
un(x,
to)
= L
ai(to)cPi(X)
= L
'I/J(Xi)cPi(X),
i=l i=l
6.4.
Finite
element
methods
for the
heat
equation
259
that
is, as
ai(to)
=
if>(xi).
This
is
reasonable, because
the
function
satisfies
We
call
V>
the
piecewise
linear
interpolant
of
tf}(x)
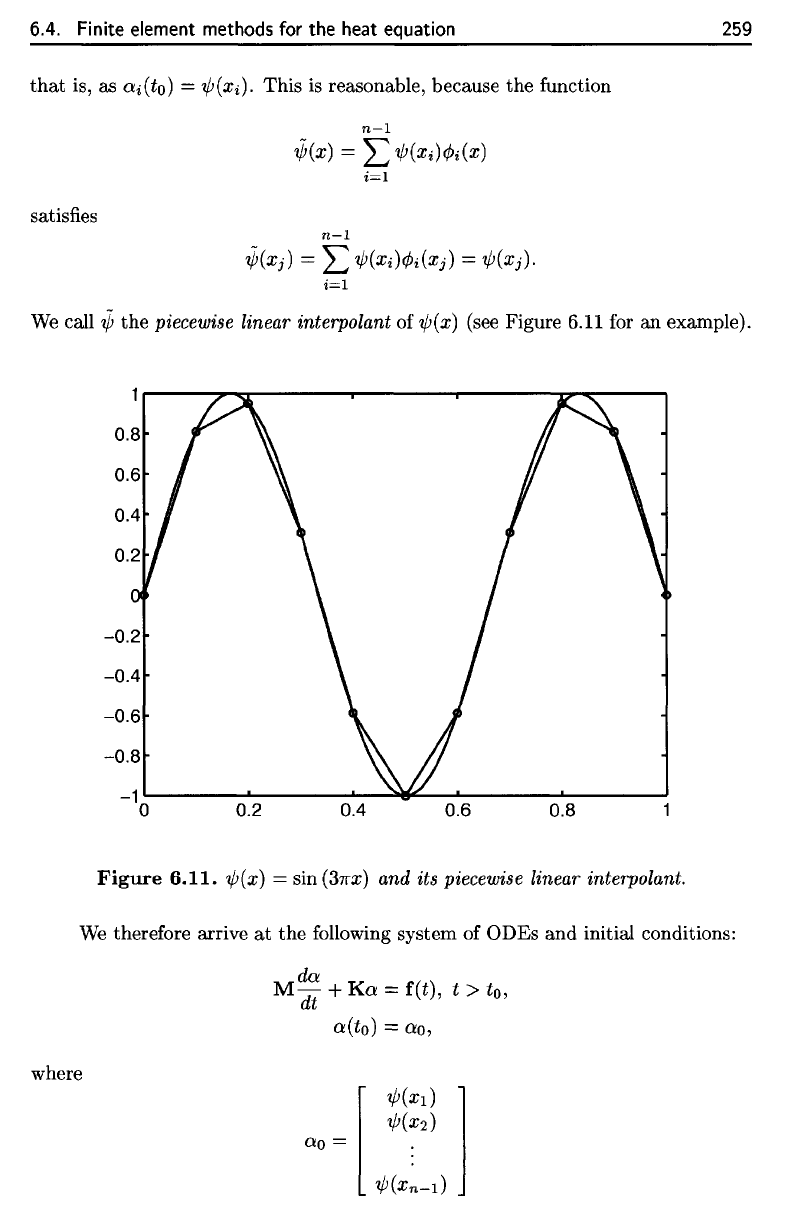
(see Figure 6.11
for an
example).
Figure
6.11.
^(x)
= sin
(STTX)
and its
piecewise
linear interpolant.
We
therefore arrive
at the
following
system
of
ODEs
and
initial conditions:
where
6.4. Finite element methods for
the
heat equation
259
that
is, as ai(to) = '¢(Xi). This is reasonable, because
the
function
n-l
,(f;(x)
= L
'¢(Xi)(Pi(X)
i=l
satisfies
n-l
,(f;(Xj)
= L
,¢(Xi)(Pi(Xj)
= '¢(Xj).
i=l
We
call
,(f;
the
piecewise linear interpolant of ,¢(x) (see Figure 6.11 for an example).
Figure
6.11.
,¢(x) = sin
(37fx)
and its piecewise linear interpolant.
We
therefore arrive
at
the
following system of ODEs and initial conditions:
dO'
M dt +
Ka
= f(t), t >
to,
aCto)
=
0'0,
where

that
is,
We
recognize this
as an
inhomogeneous
system
of
linear, constant
coefficient
first-
order ODEs
for the
unknown
a(t)
(if the
coefficients
in the PDE are
nonconstant,
then
so
will
be the
matrices
M and K and
hence
A; in
that
case,
the
system
of
ODEs will
not
have
constant
coefficients).
37
We
have
now
discretized
the
spatial
variation
of the
solution
(a
process
referred
to as
semidiscretization
in
space)
to
obtain
a
system
of
ODEs.
We can now
apply
a
numerical method
to
integrate
the
ODEs. This general technique
of
solving
a
time-dependent
PDE by
integrating
the
system
of
(semidiscrete)
ODEs
is
called
the
method
of
lines.
6.4.1
The
method
of
lines
for the
heat
equation
We
now
illustrate
the
method
of
lines
via an
example, which
will
show
that
the
system
of
ODEs arising
from
the
heat equation
is
stiff.
Example
6.8.
Suppose
an
iron
bar (p
=
7.88,
c
=
0.437,
K —
0.836,)
is
chilled
to a
constant temperature
of
0
degrees
Celsius,
and
then
heated
internally with
both
ends
maintained
at 0
degrees
Celsius.
Suppose
further that
the bar is 100 cm in
length
and
heat
energy
is
added
at the
rate
of
We
will
approximate
the
solution using piecewise linear
finite
elements with
a
regular
mesh
of
100
subintervals.
We
write
n =
100,
h
=
100/n,
Xi = ih, i =
0,1,2,...,
n.
37
In
practice,
we do not
actually compute either
M"
1
or A.
When implementing numerical
algorithms,
it is
rarely
efficient
to
compute
an
inverse matrix, particularly when
the
matrix
is
sparse,
as in
this case. Instead,
the
presence
of
M"
1
is a
signal
that
a
linear system with
coefficient
matrix
M
must
be
solved.
This
is
explained below when
we
discuss
the
implementation
of
Euler's
method
and the
backward
Euler
method.
260
Chapter
6.
Heat
flow
and
diffusion
To
solve this,
we can
multiply
the ODE on
both sides
by M
1
to
obtain
We
wish
to find the
temperature distribution
in the bar
after
3
minutes.
The
temperature distribution
u(x,t)
is the
solution
of
the
IBVP
260
Chapter
6.
Heat flow
and
diffusion
To solve this,
we
can multiply
the
ODE on
both
sides by
M~l
to obtain
that
is,
do:
dt
==
Ao:
+ get), A
==
_M~lK,
get)
==
M~lf(t).
We
recognize this as
an
inhomogeneous system of linear, constant coefficient first-
order ODEs for the unknown o:(t) (if the coefficients in the
PDE
are nonconstant,
then
so
will be
the
matrices M and K and hence
A;
in
that
case, the system of
ODEs will not have constant coefficients).
37
We
have now discretized the spatial variation of
the
solution (a process referred
to as semidiscretization in
space)
to
obtain a system
of
ODEs.
We
can now apply
a numerical method to integrate
the
ODEs. This general technique of solving a
time-dependent
PDE
by integrating
the
system of (semidiscrete) ODEs
is
called
the method
of
lines.
6.4.1 The method
of
lines
for
the heat equation
We
now illustrate
the
method of lines via
an
example, which will show
that
the
system of ODEs arising from
the
heat equation
is
stiff.
Example
6.8.
Suppose an iron
bar
(p
==
7.88, c
==
0.437,
K.
==
0.836) is chilled to a
constant temperature
of
0
degrees
Celsius, and then heated internally with
both
ends
maintained at 0
degrees
Celsius. Suppose further that the
bar
is
100 cm in length
and heat energy is added at the rate
of
We wish to find the temperature distribution in the
bar
after 3 minutes.
The temperature distribution
u(x,
t) is the solution
of
the
IBVP
au
a
2
u
pc
at
-
K.
ax
2
==
I(x,
t), 0 < x < 100, t > 0,
u(x,O)
==
0,
0 < x < 100,
(6.42)
u(O,
t)
==
0,
t > 0,
u(100,
t)
==
0,
t >
O.
We will approximate the solution using piecewise linear finite elements with a regular
mesh
of
100 subintervals.
We
write n
==
100, h
==
1001n,
Xi
==
ih,
i
==
0,1,2,
...
,
n.
37In practice, we do
not
actually
compute
either
M-l
or
A.
When
implementing numerical
algorithms,
it
is rarely efficient
to
compute
an
inverse
matrix,
particularly
when
the
matrix
is
sparse, as in
this
case. Instead,
the
presence
of
M-
1
is a signal
that
a linear
system
with
coefficient
matrix
M
must
be solved.
This
is explained below when we discuss
the
implementation
of
Euler's
method
and
the
backward
Euler
method.

We
first try
taking
N
=
180
steps
(At
=
1 s)
of
Euler's
method; however,
the
result
is
meaningless, with temperatures
on the
order
of
10
40
degrees
Celsius!
Clearly
Euler's method
is
unstable with this choice
of
At.
A
little experimentation shows that
At
cannot
be
much more than
0.7
seconds,
or
instability will result.
The
temperature
distribution
att
= 180
seconds, computed using
260
time steps
(At
=
0.69J,
is
shown
in
Figure
6.12.
Before
leaving this example,
we
should explain
how
Euler's method
is
imple-
mented
in
practice.
The
system
of
ODEs
is
6.4.
Finite
element
methods
for the
heat equation
261
As
usual,
{(f)i,
02,
• •
•,
0n-i}
will
be the
standard
basis
for the
subspace
S
n
of
con-
tinuous piecewise linear
finite
elements.
It is
straightforward
to
compute
the
mass
and
stiffness
matrices:
(both
M and K are
tridiaqonal
and
symmetric).
We
also
have
and
so
Euler's method takes
the
form
As we
mentioned
before,
it is not
efficient
to
actually compute
M
;
since
M is
tridiagonal
and
M"
1
is
completely dense. Instead,
we
implement
the
above
iteration
as
where
sW
is
found
by
solving
6.4. Finite element methods for the heat equation
261
As
usual,
{<Pl,
<P2'
...
' <Pn-d will
be
the standard basis for the subspace
Sn
of
con-
tinuous
piecewise linear finite elements.
It
is straightforward to compute the mass
and stiffness matrices:
1
100 2hpc
Mii
= pC(<Pi(X))2dx =
--,
i = 1,2,
...
,n-l,
o 3
tOO
hpc .
Mi,i+l
=
10
PC<Pi(X)<Pi+l(X)dx
=
6'
z = 1,2,
...
,n
-
2,
{lOO
(d<Pi
) 2
2K;.
Kii=
10
K;
dx(x)
dX=h'
z=1,2,
...
,n-l,
1
100
d<Pi
( )
d<Pi+l
( )
K;.
Ki
i+l
=
K;-
x
-d-
x
dx
= - -h' z = 1,2,
...
, n - 2
, 0
dx
x
(both
M and K are tridiagonal and
symmetric).
We also have
(100
fi(t)
=
10
f(x,
t)<Pi(X)
dx
h2(60000i - 200h - 1200i
2
h + 6h
2
i
3
+
3ih
2
)
= t
6.10
8
'
i = 1,2,
...
, n -
1.
We
first
try
taking N = 180 steps
(.D.t
= 1 s)
of
Euler's method; however, the result
is meaningless, with temperatures on the order
of
10
40
degrees Celsius! Clearly
Euler's method is unstable with this choice
of
.D.t.
A little experimentation shows
that
.D.t
cannot
be
much
more than 0.7 seconds, or instability will result. The temperature
distribution
at
t = 180 seconds, computed using 260
time
steps
(.D.t
==
0.69), is shown
in
Figure 6.12.
Before leaving this example, we should explain how Euler's method is imple-
mented
in
practice. The
system
of
ODEs is
da 1
dt =
M-
(-Ka
+ f(t)),
and so Euler's method takes the
form
As
we
mentioned
before,
it
is
not
efficient to actually compute
M-
l
,
since M is
tridiagonal and
M-
l
is completely dense. Instead, we
implement
the above iteration
as
where sci) is found by solving
MSCi)
=
-Ka
C
;)
+
f(ti)·
262
Chapter
6.
Heat flow
and
diffusion
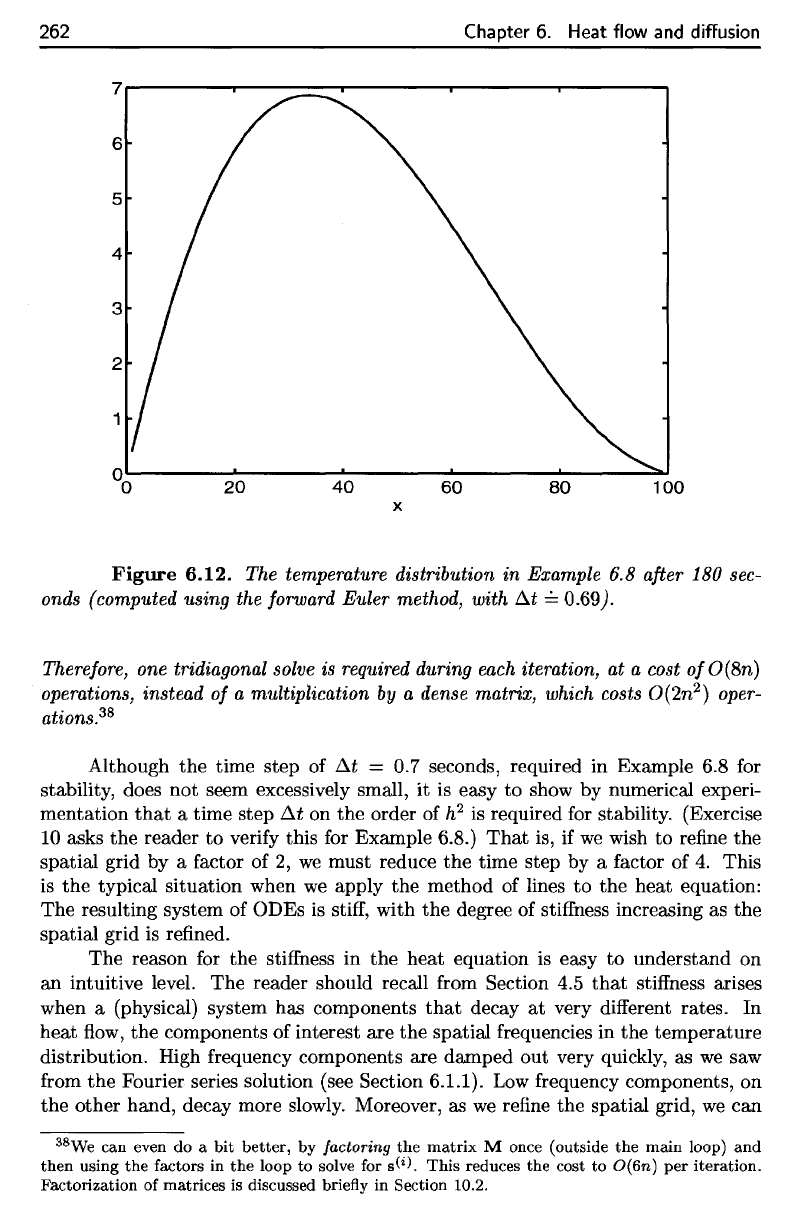
Figure
6.12.
The
temperature distribution
in
Example
6.8
after
180
sec-
onds
(computed
using
the
forward
Euler
method, with
At
=
0.69J.
Therefore,
one
tridiagonal
solve
is
required
during
each
iteration,
at a
cost
of
O(8n)
operations,
instead
of a
multiplication
by a
dense matrix, which costs
O(2n
2
)
oper-
ations.
38
Although
the
time step
of At
=
0.7
seconds, required
in
Example
6.8 for
stability, does
not
seem excessively small,
it is
easy
to
show
by
numerical experi-
mentation
that
a
time
step
At
on the
order
of h
2
is
required
for
stability. (Exercise
10
asks
the
reader
to
verify
this
for
Example 6.8.)
That
is, if we
wish
to
refine
the
spatial
grid
by a
factor
of 2, we
must reduce
the
time step
by a
factor
of 4.
This
is
the
typical situation when
we
apply
the
method
of
lines
to the
heat equation:
The
resulting system
of
ODEs
is
stiff,
with
the
degree
of
stiffness
increasing
as the
spatial
grid
is
refined.
The
reason
for the
stiffness
in the
heat
equation
is
easy
to
understand
on
an
intuitive level.
The
reader should recall
from
Section
4.5
that
stiffness
arises
when
a
(physical) system
has
components
that
decay
at
very
different
rates.
In
heat
flow, the
components
of
interest
are the
spatial frequencies
in the
temperature
distribution.
High frequency components
are
damped
out
very quickly,
as we saw
from
the
Fourier series solution (see Section
6.1.1).
Low
frequency
components,
on
the
other hand, decay more slowly. Moreover,
as we
refine
the
spatial
grid,
we can
38
We
can
even
do a bit
better,
by
factoring
the
matrix
M
once
(outside
the
main loop)
and
then
using
the
factors
in the
loop
to
solve
for
s^).
This reduces
the
cost
to
O(6n)
per
iteration.
Factorization
of
matrices
is
discussed
briefly
in
Section
10.2.
262
Chapter 6. Heat flow
and
diffusion
x
Figure
6.12.
The temperature distribution in Example 6.8 after 180 sec-
onds (computed using the forward Euler method, with
t:..t
==
0.69).
Therefore, one tridiagonal solve is required during
each
iteration, at a cost
of
O(8n)
operations, instead
of
a multiplication
by
a dense matrix, which costs O(2n2) oper-
ations.
38
Although
the
time step of
t:..t
= 0.7 seconds, required in Example 6.8 for
stability, does not seem excessively small,
it
is
easy
to
show by numerical experi-
mentation
that
a time step
t:..t
on
the
order of h
2
is required for stability. (Exercise
10 asks the reader
to
verify this for Example 6.8.)
That
is, if
we
wish to refine
the
spatial grid by a factor of
2,
we
must reduce
the
time step by a factor of
4.
This
is
the
typical situation when
we
apply the method of lines
to
the heat equation:
The resulting system of ODEs
is
stiff, with
the
degree of stiffness increasing as the
spatial grid
is
refined.
The reason for the stiffness in the heat equation
is
easy
to
understand on
an
intuitive level. The reader should recall from Section 4.5
that
stiffness arises
when a (physical) system has components
that
decay
at
very different rates. In
heat
flow,
the
components of interest are
the
spatial frequencies in the temperature
distribution. High frequency components are damped
out
very quickly, as
we
saw
from
the
Fourier series solution (see Section 6.1.1).
Low
frequency components, on
the other hand, decay more slowly. Moreover, as
we
refine the spatial grid,
we
can
38We can even do a
bit
better,
by
factoring
the
matrix
M once (outside
the
main
loop)
and
then
using
the
factors in
the
loop
to
solve for
s(i).
This
reduces
the
cost
to
O(6n)
per
iteration.
Factorization
of
matrices is discussed briefly in Section 10.2.
263
represent higher frequencies,
and so the
degree
of
stiffness
worsens.
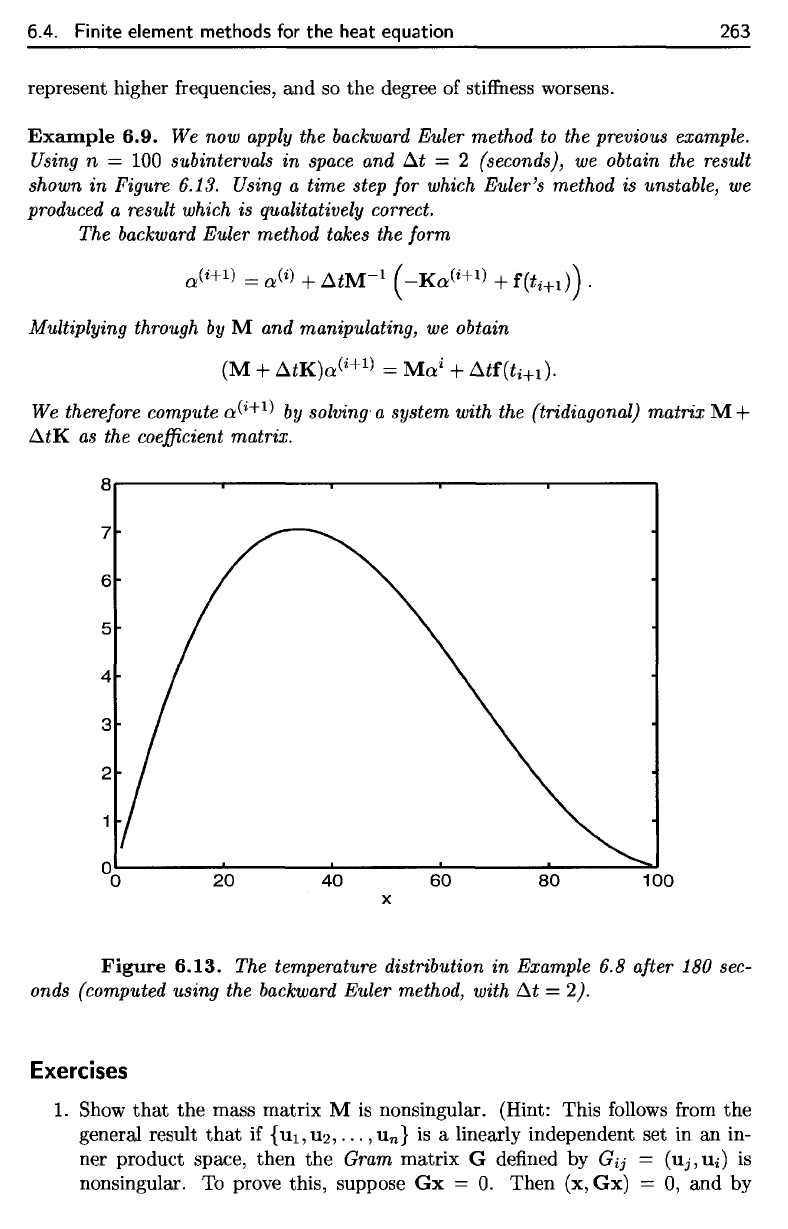
Example 6.9.
We now
apply
the
backward
Euler
method
to the
previous example.
Using
n
=
100
subintervals
in
space
and
At
= 2
(seconds),
we
obtain
the
result
shown
in
Figure
6.13.
Using
a
time step
for
which
Euler's
method
is
unstable,
we
produced
a
result which
is
qualitatively correct.
The
backward
Euler method takes
the
form
Figure 6.13.
The
temperature distribution
in
Example
6.8
after
180
sec-
onds
(computed using
the
backward
Euler method, with
At
= 1).
Exercises
Show
that
the
mass
matrix
M is
nonsingular.
(Hint:
This
follows
from
the
general result
that
if
{ui,U2,...
,u
n
}
is a
linearly independent
set in an in-
ner
product space, then
the
Gram
matrix
G
defined
by Gij =
(uj,
Uj)
is
nonsingular.
To
prove this, suppose
Gx = 0.
Then
(x, Gx) = 0, and by
6.4.
Finite
element
methods
for the
heat
equation
Multiplying
through
by M and
manipulating,
we
obtain
We
therefore
compute
a^
+1
)
by
solving
a
system with
the
(tridiagonal) matrix
M +
AtK
as the
coefficient
matrix.
6.4. Finite element methods for the heat equation
263
represent higher frequencies,
and
so
the
degree of stiffness worsens.
Example
6.9.
We now apply the backward Euler method to the previous example.
Using n = 100 subintervals
in
space and
Ilt
= 2 (seconds), we obtain the result
shown
in
Figure 6.13. Using a time step for which Euler's method is unstable,
we
produced a result which is qualitatively correct.
The backward Euler method takes the form
a(i+l)
= a(i) +
IltM-
1
(
_Ka(i+1) +
f(tHd)
.
Multiplying through
by
M and manipulating,
we
obtain
(M
+
IltK)a(Hl)
=
Ma
i
+ Iltf(ti+1).
We therefore compute
a(Hl)
by
solving a system with the (tridiagonal) matrix M +
IltK
as
the coefficient matrix.
Br--------r--------r--------r--------r---------,
x
Figure
6.13.
The temperature distribution
in
Example 6.8 after 180 sec-
onds (computed using the backward Euler method, with
Ilt
= 2).
Exercises
1. Show
that
the
mass
matrix
M
is
nonsingular. (Hint:
This
follows from
the
general result
that
if
{Ul'
U2,
...
, un}
is
a linearly
independent
set in
an
in-
ner
product
space,
then
the
Gram
matrix
G defined
by
G
ij
=
(Uj,
Ui)
is
nonsingular. To prove this, suppose
Gx
=
O.
Then
(x,
Gx)
= 0,
and
by

Use
the finite
element method, with
the
approximating
subspace
83
(and
a
regular grid),
to do the
discretization
in
space.
(a)
Explicitly compute
the
mass matrix
M, the
stiffness
matrix
K, and the
load vector
f(t).
(b)
Explicitly
set up the
system
of
ODEs resulting
from
applying
the
method
of
lines.
4.
Consider
a
heterogeneous bar,
that
is, a bar in
which
the
material properties
/9,
c, and K are not
constants
but
rather
functions
of
space:
p =
p(x),
c =
c(x),
K
=
K(X).
(a)
What
is the
appropriate
form
of the
heat
equation
for
this bar?
(b)
What
is the
appropriate weak
form
of the
resulting
IBVP
(assuming
homogeneous
Dirichlet
conditions)?
(c)
How
does
the
system
of
ODEs change?
5.
An
advantage
of the
weak formulation
of a BVP
(and therefore
of the fi-
nite element method)
is
that
the
equation makes sense
for
discontinuous
coefficients.
Consider
a
metal
bar of
length
1m and
diameter 4cm.
As-
sume
that
one-half
of the bar is
made
of
copper
(c =
0.379 J/(gK),
p =
8.97g/cm
3
,
K =
4.04
W/(cmK)),
and the
other half
is
made
of
iron (spe-
cific
heat
c =
0.437
J/(gK),
density
p =
7.88
g/cm
3
,
thermal
conductivity
K
=
0.836
W/(cmK)).
Suppose
the bar is
initially heated
to 5
degrees Celsius
and
then
(at
time
0) its
ends
are
placed
in an ice
bath
(0
degrees
Celsius).
264
Chapter
6.
Heat
flow
and
diffusion
expanding
(x, Gx) in
terms
of the
inner products
(iij,iii),
it is
possible
to
show
that
(x, Gx) = 0 is
only possible
if x = 0.
This
suffices
to
show
that
G
is
nonsingular.)
2.
Consider
a
function
/ in
C[0,^].
(a)
Show
how to
compute
the
projection
of /
onto
the
subspace
S
n
.
Be
sure
to
observe
how the
mass matrix
M and
load vector
f
arise naturally
in
this problem.
(b)
We can
also
find an
approximation
to /
from
S
n
by
computing
the
piece-
wise
linear
interpolant
of /.
Show
by a
specific
example
that
the
projec-
tion
of
/
onto
S
n
and the
piecewise linear interpolant
of /
from
S
n
are not
the
same. (The number
n can be
chosen small
to
make
the
computations
simple.)
3.
Apply
the
method
of
lines
to the
IBVP
264
Chapter
6.
Heat flow
and
diffusion
expanding (x,
Gx)
in terms of
the
inner products
(Uj,
Ui),
it
is
possible
to
show
that
(x,
Gx)
= 0
is
only possible if x =
O.
This suffices to show
that
G
is nonsingular.)
2.
Consider a function f in
e[O,
l).
(a) Show how to compute the projection of f onto
the
subspace Sn. Be sure
to
observe how the mass matrix M and load vector f arise naturally in
this problem.
(b)
We
can also find
an
approximation to f from Sn by computing the piece-
wise linear interpolant of
f. Show by a specific example
that
the
projec-
tion of f onto Sn and the piecewise linear interpolant of f from Sn are not
the
same. (The number n can be chosen small to make the computations
simple.)
3. Apply
the
method of lines to the IBVP
au
a
2
u
at
-
ax2
=
x(l
- x) cos (t), 0 < x <
1,
t > 0,
u(x,
0)
= 1, 0 < x <
1,
u(O,
t) = 0, t >
to,
u(l,
t) = 0, t > to.
Use the finite element method, with
the
approximating subspace
S3
(and a
regular grid),
to
do
the
discretization in space.
(a) Explicitly compute the mass matrix
M,
the stiffness matrix K, and the
load vector
f(t).
(b) Explicitly set up the system of ODEs resulting from applying the method
of lines.
4. Consider a heterogeneous bar,
that
is, a bar in which the material properties
p,
c,
and
'"
are not constants
but
rather
functions of space: p = p(x), c = c(x),
'"
= "'(x).
(a)
What
is
the appropriate form of the heat equation for this bar?
(b)
What
is the appropriate weak form of the resulting IBVP (assuming
homogeneous Dirichlet conditions)?
(c)
How
does the system of ODEs change?
5.
An advantage of
the
weak formulation of a
BVP
(and therefore of
the
fi-
nite element method)
is
that
the equation makes sense for discontinuous
coefficients. Consider a metal
bar
of
length 1m and diameter 4 cm. As-
sume
that
one-half of the bar
is
made of copper (c =
0.379J/(gK),
P =
8.97
g/cm
3
,
'"
= 4.04 W /(cmK)), and
the
other half
is
made of iron (spe-
cific heat c
= 0.437 J /
(g
K), density p = 7.88
g/
cm
3
,
thermal conductivity
'" = 0.836 W / (cmK)). Suppose
the
bar
is
initially heated
to
5 degrees Celsius
and
then
(at time
0)
its ends are placed in
an
ice
bath
(0
degrees Celsius).

6.4.
Finite
element
methods
for the
heat
equation
265
(a)
Formulate
the
IBVP
describing this experiment.
(b)
Apply
the finite
element method
and the
method
of
lines
to
obtain
the
resulting system
of
ODEs.
Use
only
a
uniform
grid with
an
even number
of
subintervals
(so
that
the
midpoint
of the bar is
always
a
gridpoint).
Give
the
mass matrix
M and the
stiffness
matrix
K
explicitly.
6.
Consider
the
IBVP with inhomogeneous Dirichlet conditions:
(c)
Illustrate
by
solving (6.43) with
/9,
c, K
equal
to the
material
constants
for
iron,
t =
100cm,
^)(x)
= 0
degrees Celsius,
a(t]
= 0, and
b(t)
=
sin
(607r£).
7.
Consider
the
IBVP
from
Examples
6.8 and
6.9.
(a)
Using
the
method
of
Fourier series,
find the
exact solution
u(x,t).
(b)
Using enough terms
in the
Fourier series
to
obtain
a
highly accurate
solution, evaluate
u(x,
180)
on the
regular grid with
n = 100
used
in
Examples
6.8 and
6.9.
(c)
Reproduce
the
numerical results
in
Examples
6.8 and
6.9, and,
by
com-
paring
to the
Fourier series result, determine
the
accuracy
of
each result.
8.
Repeat Example 6.8, with
the
following
changes. First, assume
that
the bar
is
made
of
copper
(p =
8.96g/cm
3
,
c =
0.385 J/(gK),
K =
4.01
W/(cmK))
instead
of
iron. Second, assume
that
the
heat "source"
is
given
by
(note
that
/
adds energy over
part
of the
interval
and
takes
it
away over
an-
other part). Graph
the
temperature
after
180
seconds. Does
the
temperature
approach
a
steady
state
as t
->•
oo?
(a)
Formulate
the
weak
form
of the
IBVP.
(b)
Show
how to
apply
the finite
element method
by
representing
the ap-
proximate solution
in the
form
u
n
(x,t)
=
v
n
(x,t)
+
g
n
(x,t),
where
and
6.4. Finite element methods for
the
heat
equation 265
(a) Formulate the IBVP describing this experiment.
(b) Apply the finite element method and the method of lines to obtain
the
resulting system of ODEs. Use only a uniform grid with
an
even number
of subintervals (so
that
the
midpoint of
the
bar
is
always a gridpoint).
Give the mass matrix M
and
the stiffness matrix K explicitly.
6.
Consider the IBVP with inhomogeneous Dirichlet conditions:
au a
2
u
pc
at
-
Ii
ax
2
=
f(x,
t), 0 < x <
£,
t > to,
u(x,
to)
= ,¢(x), 0 < x <
£,
(6.43)
u(O,
t) = a(t),
t>
to,
u(£,t) = b(t),
t>
to.
(a) Formulate
the
weak form of the IBVP.
(b) Show how
to
apply
the
finite element method by representing the ap-
proximate solution in the form
un(x, t) = vn(x, t) +
gn(X,
t), where
n-l
vn(x, t) = L Qi(t)¢i(X)
i=l
and
gn(X,
t)
= a(t)¢o(x) + b(t)¢n(x).
(c)
Illustrate by solving (6.43) with
p,
c,
Ii
equal to
the
material constants
for iron,
£ = 100cm, ,¢(x) = 0 degrees Celsius, a(t) =
0,
and b(t) =
sin
(601ft)
.
7.
Consider the IBVP from Examples 6.8 and 6.9.
(a) Using the method of Fourier series, find the exact solution
u(x, t).
(b) Using enough terms in the Fourier series to obtain a highly accurate
solution, evaluate
u(x, 180) on the regular grid with n = 100 used in
Examples 6.8 and 6.9.
(c) Reproduce the numerical results in Examples 6.8 and 6.9, and, by com-
paring
to
the Fourier series result, determine the accuracy of each result.
8. Repeat Example 6.8, with
the
following changes. First, assume
that
the
bar
is
made of copper
(p
= 8.96
g/
cm
3
,
c = 0.385 J / (g K),
Ii
= 4.01 W / (cm K))
instead of iron. Second, assume
that
the heat "source"
is
given by
f(x,
t) =
10-
7
tx(60 - x)(100 - x)
(note
that
f adds energy over
part
of
the
interval and takes
it
away over an-
other part). Graph the temperature after 180 seconds. Does the temperature
approach a steady
state
as t
-+
oo?

266
Chapter
6.
Heat
flow
and
diffusion
9.
Consider
a
heterogenous
bar of
length
100cm
whose material properties
are
given
by the
following
formulas:
p(x)
= 7.5 +
O.Ola;
g/cm
3
,
0 < x <
100,
c(x)
=
0.45
+
O.OOOlx
J/(gK),
0 < x <
100,
K(X)
= 2.5 +
0.05z
g/(cmK),
0 < x <
100.
Suppose
that
the
initial temperature
in the bar is a
uniform
5
degrees Celsius,
and
that
at t = 0
both ends
are
placed
in ice
baths
(while
the
lateral side
of
the bar is
perfectly insulated).
(a)
Formulate
the
IBVP
describing this experiment.
(b)
Formulate
the
weak
form
of the
IBVP.
(c)
Use the finite
element method with backward
Euler
integration
to
esti-
mate
the
temperature after
2
minutes.
10.
Consider Example 6.8,
and
suppose
that
the
number
of
elements
in the
mesh
is
increased
from
100 to
200,
so
that
the
mesh size
h is cut in
half. Show,
by
numerical
experimentation,
that
the
time
step
At
in the
forward Euler method
must
be
reduced
by a
factor
of
approximately
four
to
preserve
stability.
6.5
Finite
elements
and
Neumann conditions
So
far we
have only used
finite
element methods
for
problems with Dirichlet bound-
ary
conditions.
The
weak
form
of the BVP or
IBVP,
on
which
the finite
element
method
is
based, incorporates
the
Dirichlet conditions
in the
definition
of
V,
the
space
of
test
functions. When
the
weak
form
is
discretized
via the
Galerkin method,
the
boundary conditions
form
part
of the
definition
of
S
n
,
the
approximating sub-
space (see
(5.50)).
It
turns
out
that
Neumann conditions
are
even easier
to
handle
in the finite
element method.
As we
show below,
a
Neumann condition does
not
appear explicitly
in
the
weak
form
or in the
definition
of the
approximating subspace (the analogue
of
S
n
)-
For
this reason,
a
Neumann condition
is
often
called
a
natural
boundary
condition
(since
it is
satisfied automatically
by a
solution
of the
weak
form),
while
a
Dirichlet condition
is
referred
to as an
essential
boundary
condition (since
it is
essential
to
include
the
condition explicitly
in the
weak
form).
6.5.1
The
weak
form
of a BVP
with Neumann conditions
We
will
first
consider
the
(time-independent)
BVP
266
Chapter
6.
Heat
flow
and
diffusion
9.
Consider a heterogenous
bar
of length 100 cm whose material properties are
given by the following formulas:
p(x)
= 7.5 + O.01x
g/cm
3
,
0 < x < 100,
c(x)
= 0.45 +
O.OOOlx
J/(gK),
0 < x < 100,
II;(X)
= 2.5 + 0.05x
g/(cmK),
0 < x < 100.
Suppose
that
the initial temperature in the
bar
is
a uniform 5 degrees Celsius,
and
that
at
t = 0
both
ends are placed in ice
baths
(while
the
lateral side of
the
bar
is
perfectly insulated).
(a) Formulate the IBVP describing this experiment.
(b) Formulate the weak form of the IBVP.
(c)
Use
the
finite element method with backward Euler integration
to
esti-
mate
the
temperature after 2 minutes.
10. Consider Example 6.8,
and
suppose
that
the number of elements in the mesh
is
increased from 100
to
200,
so
that
the mesh size h
is
cut in half. Show, by
numerical experimentation,
that
the time step
tlt
in the forward Euler method
must
be
reduced by a factor of approximately four
to
preserve stability.
6.5 Finite elements and Neumann conditions
So
far
we
have only used finite element methods for problems with Dirichlet bound-
ary conditions. The weak form of the
BVP
or IBVP, on which the finite element
method
is
based, incorporates
the
Dirichlet conditions in
the
definition of V, the
space
of
test functions. When the weak form is discretized via the Galerkin method,
the boundary conditions form
part
of the definition of Sn, the approximating sub-
space (see (5.50)).
It
turns
out
that
Neumann conditions are even easier to handle in the finite
element method.
As
we
show below,
aN
eumann condition does not appear explicitly
in the weak form or in the definition of the approximating subspace (the analogue
of Sn). For this reason, a Neumann condition
is
often called a natural boundary
condition (since
it
is
satisfied automatically by a solution of the weak form), while
a Dirichlet condition
is
referred to as
an
essential boundary condition (since it
is
essential to include
the
condition explicitly in
the
weak form).
6.5.1 The
weak
form of a BVP with Neumann conditions
We
will first consider the (time-independent)
BVP
d (
dU)
--
k(x)-
=
lex),
dx dx
0<
x <
£,
du (0) = 0
dx '
(6.44)
du
dx(£)
=0.

6.5.
Finite
elements
and
Neumann conditions
267
To
derive
the
weak
form,
we
multiply both sides
of the
differential
equation
by a
test
function,
and
integrate
by
parts.
We
take
for our
space
of
test
functions
In
the
last step,
we use the
fact
that
The
weak
form
of
(6.44)
is
In the
context
of
(6.45),
we
refer
to
(6.44)
as the
strong
form
of the
BVP.
6.5.2 Equivalence
of the
strong
and
weak
forms
of a BVP
with
Neumann
conditions
The
derivation
of the
weak
form
(6.45) shows
that
if u
satisfies
the
original
BVP
(6.44)
(the strong
form),
then
u
also satisfies
the
weak
form.
We now
demonstrate
the
converse:
If u
satisfies
the
weak
form
(6.45)
of the
BVP, then
u
also satisfies
(6.44)—including
the
boundary conditions! This
is
quite surprising
at first
sight,
since
the
boundary conditions mentioned
in
(6.44)
are not
mentioned
in
(6.45).
We
assume
that
u
G
V and
that
(note
that
the
boundary conditions
do not
appear
in
this
definition).
Assuming
that
u
solves (6.44),
we
have,
for
each
v €
V,
Integrating
by
parts
on the
left
side
of
this equation yields
6.5. Finite elements
and
Neumann conditions
267
To derive the weak form,
we
multiply
both
sides of the differential equation by a
test function, and integrate by parts.
We
take for our space of test functions
(note
that
the
boundary conditions do not appear in this definition).
Assuming
that
u solves (6.44),
we
have, for each v E
V,
d (
du
)
-
dx
k(x)
dx
(x) v(x) = f(x)v(x), 0 < x < £
1
£ d ( dU)
1£
=}
- 0
dx
k(x)
dx
(x) v(x)
dx
= 0 f(x)v(x)
dx
[
du
] £
1£
du
dv
1£
=}
- k(x)
dx
(x)v(x) 0 + 0 k(x)
dx
(x)
dx
(x)
dx
= 0
f(x)v(x)
dx
1
£
du
dv
1£
=}
0 k(x)
dx
(x)
dx
(x)
dx
= 0
f(x)v(x)
dx.
In the last step,
we
use the fact
that
du
(0)
=
du
(£)
=
o.
dx dx
The weak form of (6.44)
is
find u E V such
that
1£
k(x)
~~
(x)
~~
(x)
dx
=
1£
f(x)v(x)
dx
for all v E
V.
(6.45)
In the context of (6.45),
we
refer
to
(6.44) as the strong form of the BVP.
6.5.2 Equivalence
of
the strong
and
weak
forms
of a
BVP
with
Neumann conditions
The derivation of the weak form (6.45) shows
that
if u satisfies the original
BVP
(6.44) (the strong form), then u also satisfies the weak form.
We
now demonstrate
the
converse:
If
u satisfies the weak form (6.45) of the BVP, then u also satisfies
(6.44)----'including the boundary conditions! This
is
quite surprising
at
first sight,
since the boundary conditions mentioned in (6.44) are not mentioned in (6.45).
We
assume
that
u E V and
that
1
£
du
dv
1£
-
o k(x)
dx
(x)
dx
(x)
dx
= 0
f(x)v(x)
dx
for all v E V.
Integrating by
parts
on the left side of this equation yields
[
du
] £
1£
d [
du
]
(£
k(x)
dx
(x)v(x) 0 - 0
dx
k(x)
dx
(x) v(x) dx =
10
f(x)v(x)
dx
for all v E
V.
(6.46)
