Gockenbach M.S. Partial Differential Equations. Analytical and Numerical Methods

238

Chapter

6.

Heat flow

and

diffusion

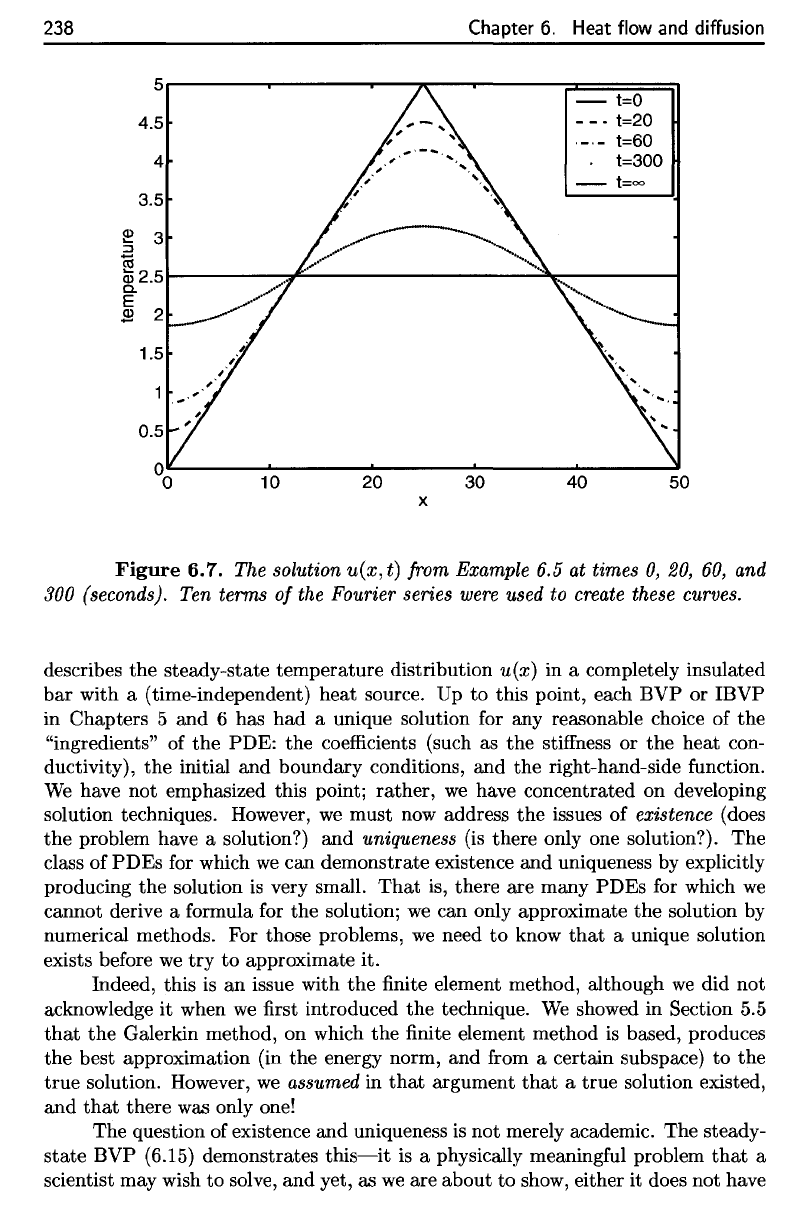
Figure

6.7.

The

solution

u(x,t]

from

Example

6.5 at

times

0, 20, 60, and

300

(seconds).

Ten

terms

of the

Fourier series

were

used

to

create

these curves.

describes

the

steady-state

temperature distribution

u(x)

in a

completely insulated

bar

with

a

(time-independent) heat source.

Up to

this point, each

BVP or

IBVP

in

Chapters

5 and 6 has had a

unique solution

for any

reasonable choice

of the

"ingredients"

of the

PDE:

the

coefficients

(such

as the

stiffness

or the

heat con-

ductivity),

the

initial

and

boundary conditions,

and the

right-hand-side function.

We

have

not

emphasized this point; rather,

we

have concentrated

on

developing

solution

techniques.

However,

we

must

now

address

the

issues

of

existence (does

the

problem have

a

solution?)

and

uniqueness

(is

there only

one

solution?).

The

class

of

PDEs

for

which

we can

demonstrate existence

and

uniqueness

by

explicitly

producing

the

solution

is

very small.

That

is,

there

are

many PDEs

for

which

we

cannot derive

a

formula

for the

solution;

we can

only approximate

the

solution

by

numerical

methods.

For

those problems,

we

need

to

know

that

a

unique solution

exists

before

we try to

approximate

it.

Indeed, this

is an

issue with

the finite

element method, although

we did not

acknowledge

it

when

we first

introduced

the

technique.

We

showed

in

Section

5.5

that

the

Galerkin method,

on

which

the finite

element method

is

based, produces

the

best approximation

(in the

energy norm,

and

from

a

certain subspace)

to the

true solution. However,

we

assumed

in

that

argument

that

a

true solution existed,

and

that

there

was

only one!

The

question

of

existence

and

uniqueness

is not

merely academic.

The

steady-

state

BVP

(6.15) demonstrates

this—it

is a

physically meaningful problem

that

a

scientist

may

wish

to

solve,

and

yet,

as we are

about

to

show, either

it

does

not

have

238

Chapter

6.

Heat flow

and

diffusion

5r-----~----~~~--~----r:==~~

--

t=O

4.5

4

3.5

~3

~

-

_.

t=20

._.-

t=60

t=300

--

t=oo

~

.,../

.........

w2.5~------------~~---------------------------~~------------~

0..

E

$ 2

10

20

30

40

50

x

Figure

6.7.

The solution

u(x,

t) from Example 6.5 at times

0,

20,

60,

and

300 (seconds). Ten terms

of

the Fourier series were used to create these curves.

describes

the

steady-state

temperature

distribution

u(x)

in a completely insulated

bar

with a (time-independent) heat source. Up

to

this point, each

BVP

or

IBVP

in Chapters 5

and

6 has

had

a unique solution for any reasonable choice of

the

"ingredients" of

the

PDE: the coefficients (such as

the

stiffness or

the

heat con-

ductivity),

the

initial

and

boundary conditions,

and

the

right-hand-side function.

We

have

not

emphasized this point; rather,

we

have concentrated on developing

solution techniques. However,

we

must

now address

the

issues of existence (does

the

problem have a solution?)

and

uniqueness (is there only one solution?).

The

class of

PDEs

for which

we

can demonstrate existence

and

uniqueness by explicitly

producing

the

solution

is

very small.

That

is, there are many

PDEs

for which

we

cannot derive a formula for

the

solution;

we

can only approximate

the

solution by

numerical methods. For those problems,

we

need

to

know

that

a unique solution

exists before

we

try

to

approximate it.

Indeed, this is

an

issue with

the

finite element method, although

we

did

not

acknowledge

it

when

we

first introduced

the

technique.

We

showed in Section 5.5

that

the

Galerkin method, on which

the

finite element method

is

based, produces

the

best approximation (in

the

energy norm,

and

from a certain subspace)

to

the

true

solution. However,

we

assumed in

that

argument

that

a

true

solution existed,

and

that

there was only one!

The

question of existence

and

uniqueness is

not

merely academic.

The

steady-

state

BVP

(6.15) demonstrates

this-it

is

a physically meaningful problem

that

a

scientist may wish

to

solve,

and

yet, as

we

are

about

to

show, either

it

does not have

6.2.

Pure Neumann conditions

and the

Fourier

cosine

series

239

a

solution

or the

solution

is not

unique!

We

already discussed this

fact

in

Examples

3.14

and

3.17

in

Section 3.2.

For

emphasis,

we

will

repeat

the

justification

from

several points

of

view.

Physical reasoning

The

source function

f(x)

in

(6.15) represents

the

rate

at

which (heat) energy

is

added

to the bar (in

units

of

energy

per

time

per

volume).

It

depends

on x

(the

position

in the

bar) because

we

allow

the

possibility

that

different

parts

of the bar

receive

different

amounts

of

heat.

However,

it is

independent

of

time, indicating

that

the

rate

at

which energy

is

added

is

constant. Clearly,

for a

steady-state solution

to

exist,

the

total

rate

at

which energy

is

added must

be

zero;

if

energy

is

added

to one

part

of the

bar,

it

must

be

taken away

from

another

part.

Otherwise,

the

total

heat

energy

in the bar

would

be

constantly growing

or

shrinking,

and the

temperature

could

not be

constant with respect

to

time.

All of

this implies

that

(6.15)

may not

have

a

solution; whether

it

does depends

on the

properties

of

/(#).

On

the

other hand,

if

(6.15) does have

a

solution,

it

cannot

be

unique. Know-

ing

only

that

no net

energy

is

being

added

to or

taken

from

the bar

does

not

tell

us

how

much energy

is in the

bar.

That

is, the

energy,

and

hence

the

temperature,

is

not

uniquely determined

by the

BVP.

Mathematical

reasoning

Recall

that

f(x)

has

units

of

energy

per

unit volume

per

unit time;

the

total

rate

at

which energy

is

added

to the bar is

where

A is the

cross-sectional

area

of the

bar.

By

physical reasoning,

we

conclude

that

or

simply

must hold

in

order

for a

solution

to

exist.

But we can see

this

directly

from

the

BVP. Suppose

u is a

solution

to

(6.15).

Then

6.2. Pure Neumann conditions

and

the Fourier

cosine

series

239

a solution or

the

solution

is

not unique!

We

already discussed this fact in Examples

3.14

and

3.17 in Section 3.2. For emphasis,

we

will repeat

the

justification from

several points of view.

Physical reasoning

The source function

f(x)

in (6.15) represents

the

rate

at

which (heat) energy

is

added to the

bar

(in units of energy per time per volume).

It

depends on x (the

position in

the

bar) because

we

allow the possibility

that

different parts of the bar

receive different amounts of heat. However, it

is

independent of time, indicating

that

the

rate

at

which energy

is

added

is

constant. Clearly, for a steady-state solution to

exist,

the

total rate

at

which energy

is

added must be zero; if energy

is

added

to

one

part

of the bar, it must be taken away from another part. Otherwise, the total heat

energy in the

bar

would be constantly growing or shrinking, and

the

temperature

could not be constant with respect

to

time.

All

of this implies

that

(6.15) may not

have a solution; whether

it

does depends on the properties of

f(x).

On

the

other hand, if (6.15) does have a solution, it cannot be unique. Know-

ing only

that

no net energy

is

being added

to

or taken from

the

bar

does not tell

us how much energy

is

in

the

bar.

That

is,

the

energy, and hence the temperature,

is

not uniquely determined by the BVP.

Mathematical reasoning

Recall

that

f(x)

has units of energy per unit volume per unit time;

the

total rate

at

which energy

is

added

to

the

bar

is

1i

f(x)Adx,

where A

is

the cross-sectional area of the bar. By physical reasoning,

we

concluded

that

1£

f(x)A

dx

= 0,

or simply

1£

f(x)

dx

= 0, (6.16)

must hold in order for a solution

to

exist.

But

we

can see this directly from

the

BVP. Suppose u

is

a solution to (6.15). Then

{l

(l

dlu

io

f(x)

dx

=

-I),

io

dx

2

(x)

dx

=

-I),~(X)

d

Ii

dx

0

du du

=

1),-(0)

- /'i,-(£)

dx

=

0-0

=

O.

where

and

thereby

satisfy

all but the first

equation.

However,

the

equation

240

Chapter

6.

Heat flow

and

diffusion

Thus,

if a

solution exists, then

the

compatibility

condition (6.16) holds.

Now

suppose

that

a

solution

u of

(6.15) does

exist.

Let C be any

constant,

and

define

a

function

v by

v(x)

=

u(x]

+

C.

Then

we

have

and

Therefore,

v is

another solution

of

(6.15),

and

this

is

true

for any

real number

C.

This shows

that

if

(6.15)

has a

solution, then

it has

infinitely

many solutions.

The

Fourier

series

method

Suppose

that,

rather than engage

in the

above reasoning,

we

just

set out to

solve

(6.15)

by the

Fourier series method. Because

of the

boundary conditions,

we

write

the

solution

as a

cosine series:

Then, computing

the

cosine

coefficients

of

—d?u/dx

2

(x)

in the

usual way,

we

have

(note

that

the

constant term

60

vanishes when

u(x)

is

differentiated).

Also,

Since

the

coefficient

co,ci,C2,...

are

given

and the

coefficients

Oo?0i

5

02,---

are to

be

determined,

we can

choose

Equating

the

series

for

—Kd?u/dx

2

(x)

and

/(#),

we find

that

the

following

equations

must hold:

240

Chapter

6.

Heat flow

and

diffusion

Thus, if a solution exists, then the compatibility condition (6.16) holds.

Now suppose

that

a solution u of (6.15) does exist. Let C be any constant,

and define a function

v by v(x) = u(x) + C. Then

we

have

~v

~u

-K,

dx

2

(x) =

-K,

dx

2

(x) + 0 =

-K,

dx

2

(x) =

f(x)

and

dv

(0)

= du

(0)

+ 0 =

du

(0)

=

0,

dv

(£)

=

du

(£)

+ 0 =

du

(£)

=

O.

dx dx dx dx dx dx

Therefore, v

is

another solution of (6.15), and this

is

true for any real number

C.

This shows

that

if (6.15) has a solution, then it has infinitely many solutions.

The

Fourier

series

method

Suppose

that,

rather

than

engage in

the

above reasoning,

we

just set out to solve

(6.15) by

the

Fourier series method. Because of

the

boundary conditions,

we

write

the solution as a cosine series:

00

u(x) =

bo

+

2::

bncos

(n;x).

n=l

Then, computing

the

cosine coefficients of

_~U/dX2(x)

in the usual

way,

we

have

~u

~

K,n

2

7r

2

(n7rx)

-K,

dx

2

(x) =

~

~bn

cos

-£-

n=l

(note

that

the

constant term b

o

vanishes when u(x)

is

differentiated). Also,

00

f(x)

=eo+

2:cnCOs(n;x),

n=l

where

1

{l

2

(l

(n7rx)

eo

= f

10

f(x)

dx, Cn = f

10

f(x)

cos

-£-

dx, n = 1,2,

....

Equating

the

series for -

K,d

2

u / dx

2

(x) and f (x),

we

find

that

the following equations

must hold:

K,n

2

7r

2

0=

Co,

~bn

=

Cn,

n = 1,2,

....

Since the coefficient

eo,Cl,C2,

... are given and

the

coefficients bo,bl,b

2

,

...

are

to

be determined,

we

can choose

and thereby satisfy all

but

the first equation. However, the equation

eo

= 0

6.2.

Pure

Neumann

conditions

and the

Fourier

cosine

series

241

is

not a

condition

on the

solution

w,

but

rather

on the

right-hand-side function

/.

Indeed,

no

choice

of u can

satisfy

this equation unless

Thus

we see

again

that

the

compatibility condition (6.16) must hold

in

order

for

(6.15)

to

have

a

solution.

Moreover,

assuming

that

CQ

= 0

does hold,

we see

that

the

value

of 60 is

undetermined

by the

BVP. Indeed, with

CQ

= 0, the

general solution

of the BVP is

where

60 can

take

on any

value. Thus, when

a

solution exists,

it is not

unique.

Relationship

to the

Fredholm alternative

for

symmetric linear systems

If

A €

R

nxn

is

symmetric

and

singular

(so

that

A/"(A)

contains nonzero

vectors),

then

the

Fredholm alternative (Theorem 3.19) implies

that

Ax = b has a

solution

if

and

only

if b is

orthogonal

to

AT

(A).

This

is the

compatibility condition

for a

symmetric,

singular linear system.

The

compatibility condition (6.16)

is

precisely

analogous,

as we now

show.

The

operator

LN

(the negative second derivative operator, restricted

to

func-

tions satisfying homogeneous Neumann conditions)

is

symmetric. Moreover,

the

null space

of the

operator

contains nonzero functions, namely,

all

nonzero solutions

to

It is

easy

to

show,

by

direct integration,

that

the

solution

set

consists

of all

constant

functions

defined

on

[0,£].

Therefore,

the

compatibility condition suggested

by the

finite-dimensional

situation

is

that

(6.15)

has a

solution

if and

only

if / is

orthogonal

to

every constant function.

But

is

equivalent

to

or

simply

to

This

is

precisely (6.16).

6.2. Pure Neumann conditions

and

the Fourier

cosine

series

241

is

not a condition on the solution u,

but

rather

on the right-hand-side function f.

Indeed, no choice of u can satisfy this equation unless

Co

=

l1£

f(x)dx

=

o.

Thus

we

see again

that

the

compatibility condition (6.16) must hold in order for

(6.15)

to

have a solution.

Moreover, assuming

that

Co

= 0 does hold,

we

see

that

the value of b

o

is

undetermined by

the

BVP. Indeed, with

Co

= 0,

the

general solution of the BVP

is

~

C

2

c

n

(n1fx)

u(x) = b

o

+

L..J

/1,n

2

1f2

cos

-C-

,

n=l

where b

o

can take on any value. Thus, when a solution exists,

it

is not unique.

Relationship to the Fredholm alternative for symmetric linear

systems

If

A E

Rnxn

is

symmetric

and

singular (so

that

N(A)

contains nonzero vectors),

then

the

Fredholm alternative (Theorem 3.19) implies

that

Ax

= b has a solution

if and only if

b is orthogonal

to

N(A).

This

is

the

compatibility condition for a

symmetric, singular linear system. The compatibility condition (6.16)

is

precisely

analogous, as

we

now show.

The

operator

LN

(the negative second derivative operator, restricted

to

func-

tions satisfying homogeneous Neumann conditions)

is

symmetric. Moreover, the

null space of the operator contains nonzero functions, namely, all nonzero solutions

to

~u

-/1,

dx

2

=

0,

0 < x <

C,

::

(0) = 0,

du(C)

=

o.

dx

(6.17)

It

is easy

to

show, by direct integration,

that

the solution set consists of all constant

functions defined on

[0,

Cl.

Therefore,

the

compatibility condition suggested by

the

finite-dimensional situation

is

that

(6.15) has a solution if and only if f

is

orthogonal

to

every constant function.

But

(c,

f)

= 0 for all c E R

is

equivalent

to

1£

cf(x)

dx = 0 for all c E

R,

or simply

to

1£

f(x)

dx =

o.

This

is

precisely (6.16).

242

Chapter

6.

Heat flow

and

diffusion

Summary

As

the

above example shows,

a

steady-state (time-independent)

BVP

with pure

Neumann

conditions

can

have

the

property

that

either there

is no

solution

or

there

is

more than

one

solution.

It is

important

to

note, however,

that

this situation

depends

on the

differential

operator

as

well

as on the

boundary conditions.

For

example,

the BVP

(K,

a > 0) has a

unique solution,

and

there

is no

compatibility condition imposed

on

/. The

difference

between (6.18)

and

(6.15)

is

that

the

differential

operator

in

(6.18) involves

the

function

u

itself,

not

just

the

derivatives

of u.

Therefore, unlike

in

problem (6.15),

the

addition

of a

constant

to u is not

"invisible"

to the

PDE.

Exercises

1.

Solve

the

IBVP

and

graph

the

solution

at

times

0,0.02,0.04,0.06,

along with

the

steady-state

solution.

2.

Solve

the

IBVP

and

graph

the

solution

at

times

0,0.02,0.04,0.06,

along with

the

steady-state

solution.

3. (a)

Show

that

Ljy

is

symmetric.

242

Chapter

6.

Heat flow

and

diffusion

Summary

As

the

above example shows, a steady-state (time-independent)

BVP

with pure

Neumann conditions can have

the

property

that

either there

is

no solution or there

is more

than

one solution.

It

is important

to

note, however,

that

this situation

depends on the differential operator as

well

as on

the

boundary conditions. For

example, the

BVP

d

2

u

-/'i,

dx

2

+ au =

f(x),

0<

x < i,

du (0) = 0,

dx

du

(i) = 0

dx

(6.18)

(/'i"

a >

0)

has a unique solution, and there

is

no compatibility condition imposed

on

f.

The

difference between (6.18) and (6.15)

is

that

the differential operator in

(6.18) involves the function

u itself, not

just

the derivatives of

u.

Therefore, unlike

in problem (6.15),

the

addition of a constant

to

u

is

not "invisible"

to

the PDE.

Exercises

1.

Solve the IBVP

au

a

2

u

at

- ax2 = 0, ° < x <

1,

t >

0,

u(x,O) =

x(I-

x),

0<

x <

1,

au

ax

(0, t) = 0, t >

0,

au

ax

(1, t) = 0, t > 0,

and

graph

the

solution

at

times 0,0.02,0.04,0.06, along with

the

steady-state

solution.

2.

Solve the IBVP

au

a

2

u 1

at

- ax2 =

"2

-

x,

° < x <

1,

t > 0,

u(x,O) =

x(I

- x),

0<

x <

1,

au

ax

(0, t) = 0, t > 0,

au

ax(I,t)

=0,

t>o

and graph

the

solution

at

times 0,0.02,0.04,0.06, along with

the

steady-state

solution.

3. (a) Show

that

LN

is symmetric.

6.2. Pure Neumann conditions

and the

Fourier cosine series

243

(b)

Show

that

the

eigenvalues

of LN are

nonnegative.

4.

Following Section 6.1.4, show

how to

solve

the

following

IBVP

with inhomo-

geneous

Neumann conditions:

5.

(a)

Consider

the

following

BVP

(with

inhomogeneous

Neumann conditions):

Just

as in the

case

of

homogeneous Neumann conditions,

if

there

is one

solution

w(x),

there

are in

fact

infinitely many solutions

u(x}+C,

where

C

is

a

constant.

Also

as in the

case

of

homogeneous Neumann conditions,

there

is a

compatibility condition

that

the

right-hand side

/(#)

must

satisfy

in

order

for a

solution

to

exist. What

is it?

(b)

Does

the BVP

(note

the

difference

in the

differential equation) require

a

compatibility

condition

on

/(#),

or is

there

a

solution

for

every

/ E

C[0,

^]?

Justify

your

answer.

6.

Consider

a

copper

bar

(p

=

8.96

g/cm

3

,

c =

0.385

J/(gK),

«

=

4.01

W/(cmK))

of

length

1 m and

cross-sectional

area

2

cm

2

.

Suppose

the

sides

and the

left

end

(x = 0) are

perfectly insulated

and

that

heat

is

added

to (or

taken

from)

the

other

end (x =

100,

x in

centimeters)

at a

rate

of

f(t)

— 0.1 sin

(QQirt)

W.

If

the

initial

(t = 0)

temperature

of the bar is a

constant

25

degrees Celsius,

find the

temperature distribution

u(x,t)

of the bar by

formulating

and

solving

an

IBVP.

6.2. Pure Neumann conditions

and

the Fourier cosine

series

243

(b) Show

that

the

eigenvalues of

LN

are

nonnegative.

4. Following Section 6.1.4, show how

to

solve

the

following

IBVP

with

inhomo-

geneous

Neumann

conditions:

au

a

2

u

pc

at

- K,

ax

2

= J(x, t), 0 < x <!!, t >

to,

u(x,

to)

=

'l/J(x),

0 < x <

!!,

au

ax

(0, t) =

aCt),

t>

to,

au

ax

(!!,

t)

=

bet),

t >

to·

5. (a) Consider

the

following

BVP

(with inhomogeneous Neumann conditions):

~u

-K,

dx

2

= J(x), 0 < x <

!!,

du

dx

(0)

=

a,

du

(!!)

=

b.

dx

Just

as in

the

case

of

homogeneous

Neumann

conditions, if

there

is one

solution

u(x),

there

are

in fact infinitely

many

solutions u(x)+C, where C

is a

constant.

Also as in

the

case of homogeneous

Neumann

conditions,

there

is a compatibility condition

that

the

right-hand

side J(x)

must

satisfy in

order

for a solution

to

exist.

What

is it?

(b) Does

the

BVP

~u

-K,

dx

2

+ u = J(x), 0 < x <

!!,

du

dx (0) = a,

dUe!!)

= b

dx

(note

the

difference in

the

differential equation) require a compatibility

condition on

I(x),

or

is

there

a solution for every I E

C[O,!!]?

Justify

your answer.

6. Consider a copper

bar

(p

= 8.96

g/

cm

3

,

c = 0.385 J / (g K), K, = 4.01 W / (cm K))

of

length

1 m

and

cross-sectional

area

2 cm

2

.

Suppose

the

sides

and

the

left

end

(x

=

0)

are

perfectly

insulated

and

that

heat

is

added

to

(or

taken

from)

the

other

end

(x

= 100, x in centimeters)

at

a

rate

of

J(t) = 0.1 sin (607rt)

W.

If

the

initial (t = 0)

temperature

of

the

bar

is a

constant

25 degrees Celsius,

find

the

temperature

distribution

u(x, t)

of

the

bar

by

formulating

and

solving

an

IBVP.

244

Chapter

6.

Heat flow

and

diffusion

7.

Consider

the

IBVP

for

some constant

(7, and

compute

C.

8.

Consider

the

experiment described

in

Exercise

6.1.8.

Suppose

that,

after

the

20

minutes

are up, the

ends

of the bar are

removed

from

the ice

bath

and are

insulated. Compute

the

eventual steady-state temperature distribution

in the

bar.

9.

Repeat

Exercise

8 for the

copper

bar

described

in

Exercise

6.1.9.

10.

Consider

an

iron

bar

(p

=

7.87

g/cm

3

,

c =

0.449

J/(gK),

K

=

0.802

W/(cm

K))

of

length

1 m and

cross-sectional

area

2

cm

2

.

Suppose

that

the bar is

heated

to

a

constant temperature

of 30

degrees Celsius,

the

left

end (x = 0) is

perfectly

insulated,

and

heat energy

is

added

to (or

taken

from)

the

right

end (x —

100)

at the

rate

of

1W

(the variable

x is

given

in

centimeters).

Suppose

further

that

heat energy

is

added

to the

interior

of the bar at a

rate

of 0.1

W/cm

3

.

(a)

Explain

why the

temperature will

not

reach steady

state.

(b)

Compute

the

temperature distribution

u(x,

t]

by

formulating

and

solving

the

appropriate IBVP,

and

verify

that

u(x,

t)

does

not

approach

a

steady

state.

(c)

Suppose

that,

instead

of the

left

end's being insulated, heat energy

is

removed

from

the

left

end of

bar.

At

what

rate

must energy

be

removed

if

the

temperature distribution

is to

reach

a

steady state?

(d)

Verify

that

your answer

to the

is

correct

by

formulating

and

solving

the

appropriate IBVP

and

showing

that

u(x,t)

approaches

a

limit.

(e)

Suppose

that

a

steady

state

is to be

achieved

by

holding

the

temperature

at the

left

end at a fixed

value. What must

the

value

be?

Explain.

11. The

purpose

of

this

exercise

is to

show

that

if

u(x,t)

satisfies homogeneous

Neumann

conditions,

and

u(x,t)

is

represented

by a

Fourier sine series, then

a

Show

that

the

solution u(x,t) satisfies

244

Chapter

6.

Heat flow

and

diffusion

7.

Consider the IBVP

au

a

2

u

at - {)x2 = 0, 0 < x < l, t >

0,

u(x,O) = 'lj;(x),

0<

x <

l,

{)u

ax

(0, t) = 0, t > 0,

{)u

ax(l,t)

= 0, t >

0.

Show

that

the

solution u(x, t) satisfies

lim

u(x, t) = C for all x E

(0,

l),

t-+oo

for some constant C, and compute

C.

8. Consider

the

experiment described in Exercise 6.1.8. Suppose

that,

after the

20

minutes are up, the ends of

the

bar are removed from the ice

bath

and are

insulated. Compute the eventual steady-state temperature distribution in the

bar.

9. Repeat Exercise 8 for

the

copper

bar

described in Exercise 6.1.9.

10. Consider

an

iron

bar

(p

= 7.87

g/cm

3

,

c =

0.449J/(gK),

K,

= 0.802 W

/(cmK))

of length 1 m and cross-sectional

area

2 cm

2

•

Suppose

that

the bar is heated

to

a constant temperature of 30 degrees Celsius,

the

left end (x = 0)

is

perfectly

insulated,

and

heat energy

is

added

to

(or taken from) the right end

(x

= 100)

at

the

rate

of 1 W (the variable x

is

given in centimeters). Suppose further

that

heat energy

is

added

to

the

interior of the

bar

at

a

rate

of

0.1

W

/cm

3

•

(a) Explain why the temperature will not reach steady state.

(b) Compute the temperature distribution

u(x, t) by formulating

and

solving

the appropriate IBVP,

and

verify

that

u(x, t) does not approach a steady

state.

(c)

Suppose

that,

instead of the left end's being insulated, heat energy

is

removed from the left end of bar. At what

rate

must energy

be

removed

if the temperature distribution is

to

reach a steady state?

(d) Verify

that

your answer to the previous

part

is

correct by formulating

and

solving the appropriate IBVP and showing

that

u(x, t) approaches

a limit.

(e)

Suppose

that

a steady

state

is

to be achieved by holding

the

temperature

at

the

left end

at

a fixed value.

What

must the value be? Explain.

11.

The

purpose of this exercise

is

to

show

that

if u(x, t) satisfies homogeneous

Neumann conditions, and

u(x, t)

is

represented by a Fourier sine series, then a

6.3.

Periodic

boundary

conditions

and the

full

Fourier

series

245

formal

calculation

of the

Fourier sine series

of

—8

2

u/dx

2

(x,

t) is

invalid.

That

is,

suppose

and u

satisfies

We

wish

to

show

that

does

not

represent

—d

2

u/dx

2

(x,t).

(a)

Show

that

the

method

of

Sections

6.1

and

6.2.2 (two

applications

of

inte-

gration

by

parts) cannot

be

used

to

compute

the

Fourier sine

coefficients

of

-d

2

u/dx

2

(x,t)

in

terms

of

ai(t),O2(t),—

(b)

Let

u(x,

t}

= t and t

—

\.

Compute

the

Fourier sine

coefficients

of

u.

Then compute

the

series (6.19),

and

explain

why it

does

not

equal

-d

2

u/dx

2

(x,t).

6.3

Periodic boundary conditions

and the

full Fourier

series

We

now

consider

the

case

of a

circular (instead

of

straight) bar, specifically,

a set

of

the

form

(see

Figure 6.8).

We can

model

the flow of

heat

in the

ring

by the

heat equation

however,

the

variable

x,

representing

the

cross-section

of the

bar,

is now

the

polar angle

9.

Purely

for

mathematical convenience,

we

will assume

that

the

length

of the bar is

21,

and we

will

label

the

cross-sections

by

x

€

(—£,^j,

where

x

=

Oi/7r.

In

particular,

x — —t and x = t now

represent

the

same cross-section

of

the

bar.

There

is an

additional level

of

approximation involved

in

modeling heat

flow in

a

circular

bar (as

compared

to a

straight

bar)

by the

one-dimensional

heat

equation.

6.3. Periodic boundary conditions

and

the

full

Fourier

series

245

formal calculation of the Fourier sine series of -()2u/ax

2

(x, t)

is

invalid.

That

is, suppose

~

.

(nnx)

2

(l

.

(nnx)

u(x, t) =

~

an(t) sm -e- , an(t) =

"£

io

u(x, t) sm -e-

dx

n=l

0

and u satisfies

au au

ax

(0, t) = ax

(e,

t) = 0 for all t >

O.

We

wish

to

show

that

(6.19)

does

not represent

-a

2

u/ax

2

(x, t).

(a) Show

that

the

method of Sections

6.1

and 6.2.2 (two applications of inte-

gration by parts) cannot be used to compute

the

Fourier sine coefficients

of

-a

2

u/ax

2

(x,

t)

in terms of

al

(t), a2(t),

....

(b) Let u(x, t) = t and e =

1.

Compute the Fourier sine coefficients

of

u.

Then compute the series (6.19), and explain why it does not equal

-a

2

u/ax

2

(x,

t).

6.3 Periodic boundary conditions and the full Fourier

series

We

now consider the case of a circular (instead of straight) bar, specifically, a set

of the form

(see Figure 6.8).

We

can model the

flow

of heat in the ring by

the

heat equation

au a

2

u

pc at - K, ax

2

=

0;

however, the variable x, representing

the

cross-section of

the

bar,

is

now related

to

the polar angle

O.

Purely for mathematical convenience,

we

will assume

that

the

length of the

bar

is

2£,

and

we

will label

the

cross-sections by x E (-e,

el,

where

x =

oe/n.

In particular, x =

-e

and

x = e now represent the same cross-section of

the

bar.

There

is

an additional level of approximation involved in modeling heat

flow

in

a circular

bar

(as compared

to

a straight bar) by the one-dimensional heat equation.

246

Chapter

6.

Heat

flow

and

diffusion

Figure

6.8.

A

circular

bar.

We

mentioned

earlier

that,

in the

case

of the

straight

bar,

if the

initial temperature

distribution

and the

heat source depend only

on the

longitudinal coordinate, then

so

does

the

temperature distribution

for any

subsequent time. This

is not the

case

for

a

circular bar,

as the

geometry suggests (for example,

the

distance

around

the

ring

varies

from

It

—

2-jrS

to

It

+

2-jrS,

depending

on the

path). Nevertheless,

the

modeling error involved

in

using

the

one-dimensional heat equation

is not

large

when

the bar is

thin (i.e. when

6 is

small compared

to

t).

We

will

consider

an

initial condition

as

before:

A

ring does

not

have physical boundaries

as a

straight

bar

does

(a

ring

has a

lateral

boundary,

which

we

still assume

to be

insulated,

but it

does

not

have "ends").

However, since

x =

—

t

represents

the

same cross-section

as

does

x =

l,we

still

have

boundary conditions:

(the temperature

and

temperature gradient must

be the

same whether

we

identify

the

cross-section

by x =

—lorbyx

=

l).

These

equations

are

referred

to as

periodic

boundary

conditions.

We

therefore wish

to

solve

the

following

IBVP:

246 Chapter

6.

Heat flow

and

diffusion

Figure

6.8.

A circular

bar.

We

mentioned earlier

that,

in the case of the straight bar, if

the

initial temperature

distribution and the heat source depend only on the longitudinal coordinate, then

so

does the temperature distribution for any subsequent time. This

is

not the case

for a circular bar, as

the

geometry suggests (for example,

the

distance around

the

ring varies from

2C

-

2m5

to

2C

+

21[(5,

depending on the path). Nevertheless, the

modeling error involved in using the one-dimensional heat equation is not large

when

the

bar

is

thin

(Le.

when 8

is

small compared

to

f).

We

will consider

an

initial condition as before:

u(x,

to)

=

'l/J(x),

-f

< x

~

f.

A ring does not have physical boundaries as a straight bar does (a ring has a lateral

boundary, which

we

still assume

to

be insulated,

but

it does not have "ends").

However, since

x =

-f

represents

the

same cross-section as does x =

f,

we

still have

boundary conditions:

ou ou

u(-f,t)

=

u(f,t),

ox

(-f,t)

=

ox(f,t),

t >

to

(the temperature and temperature gradient must be

the

same whether

we

identify

the cross-section by

x =

-f

or by x = f). These equations are referred

to

as periodic

boundary conditions.

We

therefore wish to solve the following IBVP:

ou 8

2

u

pc

8t

- fi,

ox

2

=

f(x,

t),

-f

< x <

f,

t >

to,

u(x,

to)

=

'l/J(x),

-f

< x < f,

(6.20)

u(

-f,

t) =

u(f,

t),

t>

to,

ou ou

ox

(-f,

t)

= 8x (f, t),

t>

to·

6.3. Periodic boundary conditions

and the

full

Fourier

series

247

As

we

have seen several times now,

the first

step

is to

develop

a

Fourier series

method

for the

**j

6.3.1 Eigenpairs

of

—

-£-5

under periodic boundary conditions

where

We

define

Using

techniques

that

are by now

familiar,

the

reader should

be

able

to

demonstrate

that

L

p

is

symmetric,

and

Lp

has no

negative

eigenvalues

(see

Exercise

5).

We

first

observe

that

AQ

=

0 is an

eigenvalue

of

L

p

,

and a

corresponding

eigenfunction

is

g

Q

(x)

—

I.

Indeed,

it is

straightforward

to

show

that

the

only

solutions

to

are the

constant functions.

We

next consider

positive

eigenvalues. Suppose

A

=

0

2

,

9 > 0. We

must solve

The

general solution

to the

differential

equation

is

6.3.

Periodic

boundary

conditions

and

the

full

Fourier

series

247

As

we

have seen several times now, the first step

is

to develop a Fourier series

method for the related

BVP

d

2

u

-/'i,

dx

2

=

lex),

-f::;

x <

f,

u(

-f)

= u(f),

(6.21)

du

(-f)

=

du

(f).

dx dx

6.3.1 Eigenpairs

of

-

d~2

under periodic boundary conditions

We

define

Lp:

C;[-f,fJ-t

C[-f,fJ

by

where

C;[-f,f]

=

{u

E C

2

[-f,f]

:

u(-f)

= u(f),

~~(-f)

=

~~(f)}.

Using techniques

that

are by now familiar, the reader should be able

to

demonstrate

that

•

Lp

is

symmetric,

and

•

Lp

has no negative eigenvalues

(see Exercise 5).

We

first observe

that

AO

= 0

is

an eigenvalue of L

p

,

and a corresponding

eigenfunction

is

go(x) = 1. Indeed, it

is

straightforward

to

show

that

the only

solutions

to

d

2

u

- dx

2

= 0,

-f

< x <

f,

u(

-e)

= u(£),

dUe_f) =

dUCf)

dx dx

are the constant functions.

We

next consider positive eigenvalues. Suppose A = (j2, 0 >

O.

We

must solve

~u

2

--=Ou

-f<x<f

dx

2

,-

,

u( -E) =

u(E),

(6.22)

du

C

-E)

=

du

(E).

dx dx

The general solution

to

the

differential equation

is

u(x) =

Cl

cos

(Ox)

+

C2

sin

(Ox).

Gockenbach M.S. Partial Differential Equations. Analytical and Numerical Methods

Подождите немного. Документ загружается.