Gockenbach M.S. Partial Differential Equations. Analytical and Numerical Methods
Подождите немного. Документ загружается.


208
Chapter
5.
Boundary
value
problems
in
statics
3.
Consider
the BVP
(a)
Using physical reasoning
(as on
page 205), determine
a
formula
for the
Green's
function
in the
case
that
k is
constant.
(b)
Derive
the
Green's function
for the BVP
(with
a
possibly
nonconstant
k}
by
integrating
the
differential equation twice
and
interchanging
the
order
of
integration
in the
resulting double integral.
(c)
Simplify
the
Green's
function
found
in
Exercise
3b in the
case
that
the
stiffness
k is
constant. Compare
to the
result
in
part
3a.
(d)
Use the
Green's
function
to
solve (5.66)
for
1=1,
f(x)
=
x,
k(x)
=
1
+ x.
4.
Consider
the BVP
(a)
Using physical reasoning
(as in the
text),
determine
a
formula
for the
Green's
function
in the
case
that
k is
constant. (Hint: Since
the bar
is
homogeneous,
the
displacement
function
u(x)
=
g(x;
y)
(y fixed)
will
be
piecewise linear, with
w(0)
=
u(i)
= 0.
Determine
the
displacement
of
the
cross-section
at x = y by
balancing
the
forces
and
using Hooke's
law,
and
then
the
three values
w(0),
u(y],
and
u(i]
will
determine
the
displacement function.)
(b)
Derive
the
Green's function
for the
BVP, still assuming
that
k is
constant,
by
integrating
the
differential equation twice
and
interchanging
the
order
of
integration
in the
resulting double integral.
Verify
that
you
obtain
the
same formula
for the
Green's function.
(c)
(Hard)
Derive
the
Green's function
in the
case
of a
nonconstant
stiffness
k(x).
5.
Since
the BVP
(5.61)
is
linear,
the
principle
of
superposition holds,
and the
solution
to
208
Chapter
5.
Boundary
value
problems
in
statics
3. Consider the
BVP
d ( dU)
-
dx
k(x)dx
=/(x),O<x<f,
::
(0)
=
0,
(5.66)
u(f) =
O.
(a) Using physical reasoning (as on page 205), determine a formula for the
Green's function in the case
that
k
is
constant.
(b) Derive the Green's function for the
BVP
(with a possibly nonconstant
k)
by integrating
the
differential equation twice and interchanging
the
order of integration in the resulting double integral.
(c)
Simplify
the
Green's function found in Exercise 3b in the case
that
the
stiffness k
is
constant. Compare to the result in
part
3a.
(d) Use the Green's function
to
solve (5.66) for f =
1,
I(x)
=
x,
k(x) =
l+x.
4.
Consider the
BVP
d ( dU)
- dx k(x) dx =
I(x),
0 < x < f,
u(O)
= 0,
u(f) =
O.
(a) Using physical reasoning (as in
the
text), determine a formula for
the
Green's function in the case
that
k is constant. (Hint: Since the bar
is
homogeneous,
the
displacement function u(x) = g(x;y)
(y
fixed) will
be piecewise linear, with
u(O)
= u(f) =
O.
Determine
the
displacement
of
the
cross-section
at
x = y by balancing the forces and using Hooke's
law, and then the three values
u(O),
u(y), and u(f) will determine the
displacement function.)
(b) Derive the Green's function for the BVP, still assuming
that
k
is
constant,
by integrating the differential equation twice and interchanging the order
of integration in
the
resulting double integral. Verify
that
you obtain the
same formula for the Green's function.
(c)
(Hard)
Derive the Green's function in the case of a nonconstant stiffness
k(x).
5. Since the
BVP
(5.61)
is
linear, the principle of superposition holds, and the
solution
to
d ( dU)
-
dx
k(x)
dx
=
I(x),
0 < x < f,
u(O)
= 0,
kef)
du
(f) = p
dx

5.7.
Green's
functions
for
BVPs
209
is
u(x)
—
w(x)
+
v(x),
where
w
solves (5.61) (hence
w
is
given
by
(5.62))
and
v
solves
Solve
(5.67)
and
show
that
the
solution
can be
written
in
terms
of the
Green's
function
(5.63).
6.
Prove directly
that
(5.65) holds. (Hint: Write
and
rewrite
as the sum of two
integrals,
Then
apply integration
by
parts
to the first
integral,
and
simplify.)
7.
Let
g(x;
y) be the
Green's
function
for the BVP
The
purpose
of
this problem
is to
derive
the
Fourier sine series
of
g(x]
y) in
three
different
ways. Since
g
depends
on the
parameter
y,
its
Fourier sine
coefficients
will
be
functions
of
y.
(a)
First
compute
the
Fourier sine series
of
g(x;
y)
directly
(that
is,
using
the
formula
for the
Fourier sine
coefficients
of a
given
function),
using
the
formula
for g as
determined
in
Exercise
4.
(b)
Next, derive
the
Fourier sine series
of
g(x;
y) as
follows:
Write down
the
Fourier
series
solution
to the
BVP.
Pass
the
summation
through
the
integral
defining
the
Fourier
coefficients
of the
right-hand side
/.
Identify
the
Fourier sine series
of the
Green's function
g(x;
y).
5.7. Green's functions for BVPs
209
is
u(x) = w(x) + vex), where w solves (5.61) (hence w
is
given by (5.62))
and
v solves
d (
dU)
- dx k(x) dx = 0, ° < x <
f,
u(o)
= 0,
(5.67)
du
kef) dx (f) =
p.
Solve (5.67) and show
that
the solution can be written in terms of the Green's
function (5.63).
6. Prove directly
that
(5.65) holds. (Hint: Write
and rewrite
{
};Y dz
g(x;
y)
=
fOx
k~~)'
Jo
k(z)'
y <
x,
x<y
fot
g(x;
y)(K
u)(y)
dy
as
the
sum of two integrals,
fox
g(x; y)(Ku)(y) dy +
it
9(Xiy)(Ku)(y) dy.
Then apply integration by parts to the first integral, and simplify.)
7.
Let g(x;
y)
be
the
Green's function for the BVP
tPu
-k
dx
2
=
I(x),
° < x <
f,
u(o)
=
0,
u(f) =
0.
The purpose of this problem
is
to
derive the Fourier sine series of g(x;
y)
in
three different ways. Since
9 depends on the parameter
y,
its Fourier sine
coefficients will be functions of
y.
(a) First compute the Fourier sine series of g(x;
y)
directly
(that
is, using
the
formula for the Fourier sine coefficients of a given function), using
the
formula for 9 as determined in Exercise
4.
(b) Next, derive the Fourier sine series of g(x;
y)
as follows: Write down
the
Fourier series solution to the BVP. Pass
the
summation through the
integral defining the Fourier coefficients of the right-hand side
I.
Identify
the
Fourier sine series of the Green's function g(x; y).

210
Chapter
5.
Boundary value problems
in
statics
(c)
Find
the
Fourier sine
series
of
g(x;y)
by
solving
the BVP
using
the
Fourier series method.
Use the
sifting
property
of the
delta
function
to
determine
its
Fourier
coefficients.
Verify
that
all
three methods give
the
same result.
5.8
Suggestions
for
further
reading
We
have
now
introduced
the two
primary topics
of
this book, Fourier series
and
finite
elements. Fourier analysis
has
been important
in
applied mathematics
for 200
years,
and
there
are
many books
on the
subject.
A
classic introductory textbook
is
Churchill
and
Brown [10],
which
has
been
in
print
for
over
60
years!
A
classic
reference
to the
theory
of
Fourier series
is
Zygmund
[53].
Two
modern textbooks
that
focus
on
Fourier series methods
are
Bick
[4] and
Hanna
and
Rowland
[24].
One
can
also look
to
introductory books
on
PDEs
for
details about Fourier
series,
in
addition
to
other analytic
and
numeric techniques. Strauss [46]
is a
well-
written
text
that
concisely surveys analytic methods.
It
contains
a
range
of
topics,
from
elementary
to
relatively advanced. Another introduction
to
PDEs
that
covers
Fourier series methods,
as
well
as
many other topics,
is
Haberman
[22].
The finite
element method
is
much more recent, having been popularized
in
the
1960s. Most textbooks
on the
subject
are
written
at a
more demanding
level
than
is
ours. Brenner
and
Scott
[6] is a
careful
introduction
to the
theory
of
finite
elements
for
steady-state problems,
while
Johnson [27]
and
Strang
and Fix
[45]
treat
both
steady-state
and
time-dependent equations. Ciarlet [11]
is
another
careful
treatment
of the
theory
of finite
elements
for
steady-state
problems.
There
is
also
the
six-volume
Texas
Finite Element Series
by
Becker, Carey,
and
Oden [3],
which
starts
at an
elementary level.
210 Chapter
5.
Boundary value problems in statics
(c) Find
the
Fourier sine series of
g(x;y)
by solving the
BVP
cPu
-k
dx
2
= J(x - y), 0 < x <
J!.,
u(O)
= 0,
u(J!.)
= 0
using the Fourier series method. Use the sifting property of the delta
function to determine its Fourier coefficients.
Verify
that
all three methods give
the
same result.
5.8 Suggestions for further reading
We have now introduced
the
two primary topics of this book, Fourier series and
finite elements. Fourier analysis has been important in applied mathematics for
200
years, and there are many books on
the
subject. A classic introductory textbook
is
Churchill and Brown
[10],
which has been in print for over
60
years! A classic
reference
to
the theory of Fourier series
is
Zygmund
[53].
Two modern textbooks
that
focus on Fourier series methods are Bick
[4]
and Hanna and Rowland
[24].
One can also look to introductory books on PDEs for details about Fourier
series, in addition to other analytic
and
numeric techniques. Strauss
[46]
is a well-
written
text
that
concisely surveys analytic methods.
It
contains a range of topics,
from elementary to relatively advanced. Another introduction
to
PDEs
that
covers
Fourier series methods, as
well
as many other topics,
is
Haberman
[22].
The
finite element method
is
much more recent, having been popularized
in the 1960s. Most textbooks on
the
subject are written
at
a more demanding
level
than
is
ours. Brenner and Scott
[6]
is
a careful introduction
to
the theory of
finite elements for steady-state problems, while Johnson
[27J
and Strang
and
Fix
[45J
treat
both
steady-state and time-dependent equations. Ciarlet
[11J
is
another
careful treatment of
the
theory of finite elements for steady-state problems. There
is
also the six-volume
Texas
Finite Element Series by Becker, Carey, and Oden
[3],
which
starts
at
an
elementary level.

Chapter
6
and
diffusion
We
now
turn
our
attention
to
time-dependent problems, still restricting ourselves
to
problems
in one
spatial
dimension. Since both time
(t) and
space
(x)
are
inde-
pendent variables,
the
differential
equations
will
be
PDEs,
and we
will
need initial
conditions
as
well
as
boundary conditions.
We
begin
with
the
heat
equation,
This
PDE
models
the
temperature distribution
u(x,t)
in a bar
(see Section 2.1)
or
the
concentration
w(ar,
t]
of a
chemical
in
solution (see Section
2.1.3).
Since
the first
time derivative
of the
unknown appears
in the
equation,
we
need
a
single initial
condition.
Our
first
model problem
will
be the
following
initial-boundary value problem
(IBVP):
We
apply
the
Fourier series method
first and
then turn
to the finite
element method
We
close
the
chapter with
a
look
at
Green's functions
for
this
and
related
problems
Along
the way we
will
introduce
new
combinations
of
boundary conditions.
6.1
Fourier series methods
for the
heat
equation
We
now
solve (6.1) using Fourier series. Since
the
unknown
u(x,t]
is a
function
of
both time
and
space,
it can be
represented
as a
Fourier sine series
in
which
the
Fourier
coefficients
depend
on t. In
other words,
for
each
£,
we
have
a
Fourier sine
211
Heat flow
ow and diffusion
We
now
turn
our attention to time-dependent problems, still restricting ourselves
to problems in one spatial dimension. Since
both
time (t) and space (x) are inde-
pendent variables,
the
differential equations will be PDEs, and
we
will need initial
conditions as well as boundary conditions.
We
begin with the heat equation,
au
a
2
u
pc
at
- /'i,
ax
2
=
f(x,
t),
0<
x <
e,
t > to·
This
PDE
models the temperature distribution
u(x,
t)
in a
bar
(see Section 2.1) or
the concentration
u(x,
t) of a chemical in solution (see Section 2.1.3). Since the first
time derivative of
the
unknown appears in the equation,
we
need a single initial
condition.
Our first model problem will be
the
following initial-boundary value problem
(IBVP):
au
a
2
u
pc
at
- /'i,
ax
2
=
f(x,
t),
0<
x <
e,
t>
to,
u(x,
to) =
'I/J(x),
0 < x <
e,
(6.1)
u(O,
t) = 0, t > to,
u(e, t) = 0, t > to.
We
apply the Fourier series method first and then
turn
to
the
finite element method.
We
close the chapter with a look
at
Green's functions for this and related problems.
Along the way
we
will introduce new combinations of boundary conditions.
6.1 Fourier
series
methods for the heat equation
We
now solve (6.1) using Fourier series. Since the unknown
u(x,
t)
is
a function
of
both
time and space,
it
can be represented as a Fourier sine series in which the
Fourier coefficients depend on
t.
In other words, for each t,
we
have a Fourier sine
211

212
Chapter
6.
Heat
flow
and
diffusion
series
representation
of
u(x,t)
(regarded
as a
function
of
x).
The
series takes
the
form
The
function
u
will
then automatically
satisfy
the
boundary conditions
in
(6.1).
We
must choose
the
coefficients
a
n
(t)
so
that
the PDE and
initial condition
are
satisfied.
We
represent
the
right-hand side
f(x,t]
in the
same way:
We
then express
the
left-hand side
of the PDE as a
Fourier series,
in
which
the
Fourier
coefficients
are all
expressed
in
terms
of the
unknowns
ai(i),
a^t],
To
do
this,
we
have
to
compute
the
Fourier
coefficients
of the
functions
and
Just
as
with
the
function
u
itself,
we are
using
the
Fourier series
to
represent
the
spatial
variation (i.e.
the
dependence
on
x}
of
these
functions.
Since they also
depend
on
t,
the
resulting Fourier
coefficients
will
be
functions
of t.
To
compute
the
Fourier
coefficients
of
we
integrate
by
parts twice, just
as we did in the
previous chapter,
and use the
boundary
conditions
to
eliminate
the
boundary terms:
212
Chapter
6.
Heat
flow
and diffusion
series representation of
u(x,
t) (regarded as a function of
x).
The series takes the
form
~
.
(n1l'x)
2
(i
.
(n1l'x)
u(x,
t) =
~
an(t) sm
-,,-
, an(t) = e
10
u(x,
t)
sm
-,,-
dx.
n=l
0
The function u will then automatically satisfy
the
boundary conditions in (6.1).
We
must choose the coefficients an(t) so
that
the
PDE
and initial condition are
satisfied.
We
represent the right-hand side f(x, t) in
the
same way:
00
i
f(x, t) = L cn(t) sin
(n;x),
cn(t) =
~
1 f(x, t) sin
(n;x)
dx.
~l
0
We
then express
the
left-hand side of the
PDE
as a Fourier series, in which the
Fourier coefficients are all expressed in terms of
the
unknowns
al
(t), a2 (t), . ... To
do
this,
we
have
to
compute the Fourier coefficients of the functions
au
pc
at
(x, t)
and
a
2
u
-1'0
ax
2
(x,
t).
Just
as with the function u itself,
we
are using the Fourier series
to
represent the
spatial variation
(Le.
the dependence on x) of these functions. Since they also
depend on
t,
the
resulting Fourier coefficients will be functions of t.
To compute the Fourier coefficients of
a
2
u
-1'0
ax
2
(x,
t),
we
integrate by parts twice,
just
as
we
did in the previous chapter, and use the
boundary conditions
to
eliminate
the
boundary terms:
21'0
{i
cPu
(n1l'x)
-7
10
ax
2
(x,
t) sin -e-
dx
= _
21'0
([au
(x,
t) sin
(n1l'x)]
£ _
n1l'
{l
au
(x,
t)
cos
(n1l'x)
dX)
e
ax
"0"
10
ax
"
21'On1l'
{i
au
(n1l'x)
=
~
10
ax
(x,
t) cos
-,,-
dx
~
2;:,
([
u(x, t)
008
C;X)
1:
+ n
e
,
[u(x,
t) sin
C;X)
dx )
21'On
2
1l'2
(i
(n1l'X)
=
,,3
10
u(x,
t) sin
-,,-
dx
I'On
2
1l'2
=
i2
an
(t).

the PDE
implies
These
conditions provide initial conditions
for the
ODEs.
To find
a
n
(t),
we
solve
the
IVP
6.1. Fourier
series
methods
for the
heat
equation
213
We
used
the
conditions
sin (0) = sin
(n?r)
= 0 and
w(0,
t]
=
u(l,t)
= 0 in
canceling
the
boundary terms
in the
above calculation.
We
now
compute
the
Fourier sine
coefficient
of
pcdu/dt.
Using Theorem 2.1,
we
have
Thus
the nth
Fourier
coefficient
of
pcdu/dt
is
We
now see
that
Since
where
61,62;
• • •
are
the
Fourier sine
coefficients
of
ijj(x).
Therefore,
we
obtair
This
is a
sequence
of
ODEs
for the
coefficients
ai(£),a2(£),a3(£),
—
Moreover,
we
have
6.1. Fourier
series
methods for the heat equation
213
We
used
the
conditions sin
(0)
= sin
(n1f)
= 0
and
u(O,
t) = u(£, t) = 0 in canceling
the
boundary terms in
the
above calculation.
We
now compute
the
Fourier sine coefficient of pc8uj8t. Using Theorem 2.1,
we
have
2
t·
8u . (n1fx) d
[2
[f.
. (n1fx) 1
e
10
at
(x, t) sm
-f.-
dx =
dt
e
10
u(x, t) sm
-f.-
dx
d
= dt[an(t)]
_
dan
( )
- t .
dt
Thus
the
nth
Fourier coefficient of pc8uj8t is
We
now see
that
Since
CXl
f(x,
t) = L
Cn(t)
sin
(n;x),
n=l
the
PDE
implies
This is a sequence of ODEs for
the
coefficients al(t),a2(t),a3(t),
....
Moreover,
we
have
u(x,
to)
=
'ljJ(x),
0 < x <
f.
:::}
I: an(to) sin
(n;x)
=
I:bnsin(n;x),
n=l
n=l
where b
1
,
b
2
,
...
are
the
Fourier sine coefficients of
'ljJ(x).
Therefore,
we
obtain
an(to) = b
n
, n =
1,2,3,
....
These conditions provide initial conditions for
the
ODEs. To find an(t),
we
solve
the
IVP
dan
K,n
2
1f2
pCTt
+
~an
= cn(t),
(6.2)
an(to) = b
n
.

214
Chapter
6.
Heat flow
and
diffusion
The
coefficients
c
n
(t]
and
b
n
are
computable
from
the
given functions
f(x,t)
and
$(%)•
The
IVP
(6.2)
is of the
type considered
in
Section 4.2.3,
and we
have
a
formula
for
the
solution:
6.1.1
The
homogeneous
heat
equation
We
will begin with examples
of the
homogeneous
heat
equation.
Example
6.1.
We
consider
an
iron bar,
of
length
50cm,
with
specific
heat
c —
0.437
J/(gK),
density
p =
7.88
g/cm
3
,
and
thermal conductivity
K
=
0.836
Wf(cmK).
We
assume that
the bar is
insulated
except
at the
ends
and
that
it is
(somehow) given
the
initial temperature
where
^(x)
is
given
in
degrees
Celsius. Finally,
we
assume that,
at
time
t — 0, the
ends
of the bar are
placed
in an ice
bath
(0
degrees
Celsius).
We
will
compute
the
temperature
distribution
after
20, 60, and 300
seconds.
We
must solve
the
IBVP
The
solution
is
where
the
coefficient
a
n
(t)
satisfies
the IVP
and
The
coefficient
a
n
is
given
by
214
Chapter
6.
Heat
flow
and diffusion
The
coefficients cn(t)
and
b
n
are
computable from
the
given functions
f(x,
t)
and
'lj;(x).
The
IVP
(6.2) is of
the
type
considered
in
Section 4.2.3,
and
we
have a formula.
for
the
solution:
(6.3)
6.1.1 The homogeneous heat equation
We
will begin with examples of
the
homogeneous
heat
equation.
Example
6.1.
We consider an iron
bar,
of
length 50 cm, with specific heat c =
0.437
J/(gK),
density p = 7.88
g/
cm
3
,
and thermal conductivity K, = 0.836
W/(cmK).
We assume that the
bar
is insulated except at the ends and that
it
is (somehow) given
the initial temperature
1
'lj;(x)
= 5 -
Six
-
251,
where'lj;(x) is given in degrees Celsius. Finally,
we
assume that,
at
time
t = 0, the
ends
of
the bar are placed
in
an ice bath
(0
degrees Celsius). We will compute the
temperature distribution after 20,
60,
and 300 seconds.
We
must
solve the
IBVP
The solution is
au
a
2
u
pc
at
- K,
ax
2
= 0, 0 < x < 50, t > 0,
u(x,O) = 'lj;(x), 0 < x < 50,
u(O, t) = 0, t >
0,
u(50, t) = 0, t >
O.
00
u(x,t)
=
Lan(t)
sin
(n:a
x
) ,
n=l
where the coefficient an(t) satisfies the
IVP
dan
K,n
2
7r
2
dt
+
502pc
an = 0,
an(O) = b
n
and
b
=
~
(50
"1.(
) . (n7rx) d = 40 sin
(n7r
/2)
n £
10
'I'
X
sm
50 x
7r
2
n
2
'
The coefficient an is given
by
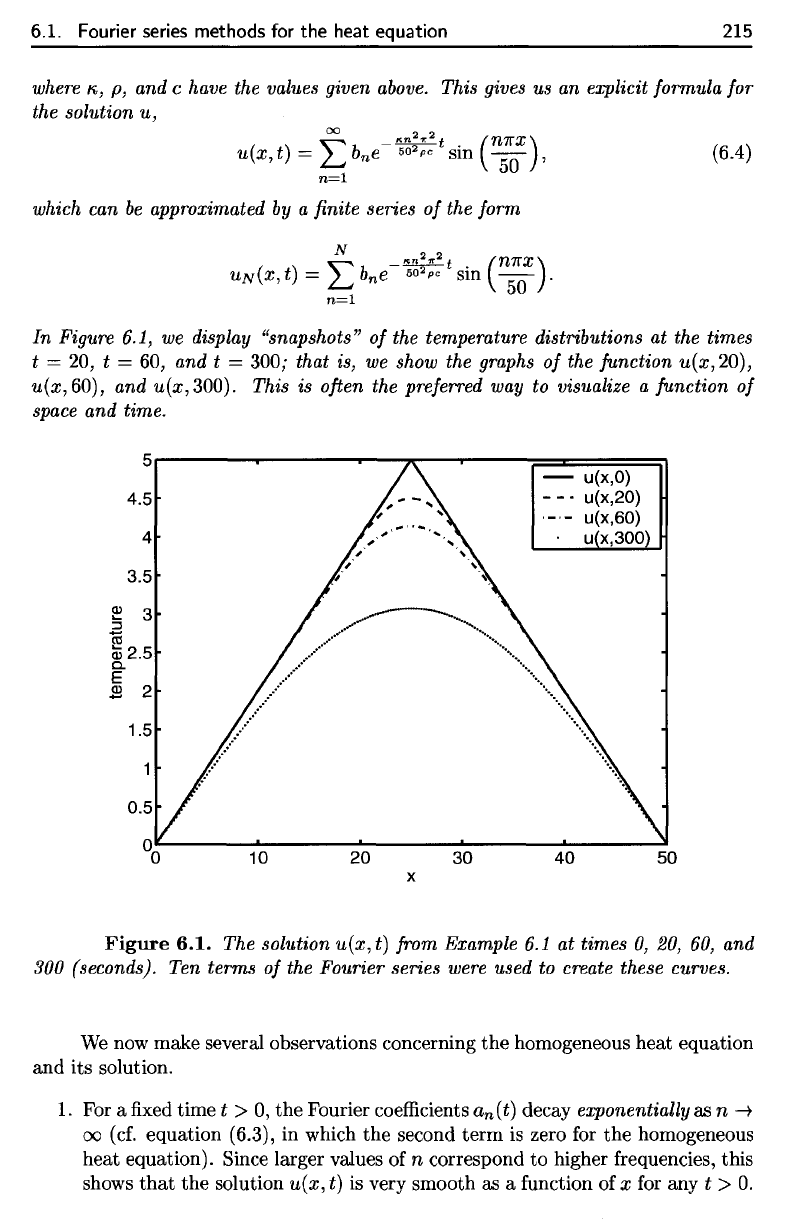
6.1. Fourier
series
methods
for the
heat equation
215
where
K,
p, and c
have
the
values given
above.
This
gives
us an
explicit
formula
for
the
solution
u,
Figure
6.1.
The
solution
u(x,t)
from Example
6.1 at
times
0, 20, 60, and
300
(seconds).
Ten
terms
of the
Fourier series
were
used
to
create
these curves.
We
now
make several observations concerning
the
homogeneous
heat
equation
and
its
solution.
1.
For a fixed
time
t > 0, the
Fourier
coefficients
a
n
(t]
decay
exponentially
as
n
—>•
oo
(cf. equation (6.3),
in
which
the
second term
is
zero
for the
homogeneous
heat
equation).
Since larger values
of n
correspond
to
higher frequencies, this
shows
that
the
solution
u(x,t)
is
very smooth
as a
function
of x for any t > 0.
which
can be
approximated
by a finite
series
of the
form
In
Figure 6.1,
we
display
"snapshots"
of
the
temperature distributions
at the
times
t =
20,
t = 60, and t =
300; that
is, we
show
the
graphs
of
the
function
w(x,20),
u(x,QQ),
and
u(x,3QO).
This
is
often
the
preferred
way to
visualize
a
function
of
space
and
time.
6.1. Fourier series methods for
the
heat equation
215
where Ib, p, and c have the values given above. This gives us an explicit formula for
the solution
u,
00
_ "n
2
,,2
t
n7fX
u(x,
t) = L bne
50
2
pc
sin
(50)'
n=l
(6.4)
which can
be
approximated by a finite series
of
the form
In
Figure 6.1,
we
display "snapshots"
of
the temperature distributions at the times
t = 20, t = 60, and t = 300; that is, we show the graphs
of
the junction
u(x,20),
u(x,60),
and
u(x,300).
This is often the preferred way to visualize a junction
of
space and time.
Sr-----~----~--~--~--~======~
u(x,O)
4.S
4
3.S
~
3
~
til
Cii2.S
c..
E
2 2
1.S
10
20
30
40
x
u(x,20)
u(x,60)
u x,300)
so
Figure
6.1.
The solution
u(x,
t) from Example 6.1 at times
0,
20,
60,
and
300 (seconds). Ten terms
of
the Fourier series were used to create these curves.
We
now make several observations concerning
the
homogeneous heat equation
and its solution.
1. For a fixed time t >
0,
the Fourier coefficients an(t) decay exponentially as n
-+
00
(cf.
equation (6.3), in which the second
term
is
zero for the homogeneous
heat equation). Since larger values of
n correspond to higher frequencies, this
shows
that
the
solution
u(x,
t) is very smooth as a function of x for any t >
O.

216
Chapter
6.
Heat
flow
and
diffusion
This
can be
seen
in
Figure 6.1;
at t
=
0, the
temperature distribution
has a
singularity
(a
point
of
nondifferentiability)
at x = 25.
This singularity
is not
seen even
after
10
seconds.
In
fact,
it can be
shown mathematically
that
the
solution
u(x,
t) is
infinitely
differentiate
as a
function
of x for
every
t > 0,
and
this holds
for
every initial temperature distribution
ty
£
(7[0,^].
The
relationship
between
the
smoothness
of a
function
and the
rate
of
decay
of
its
Fourier
will
be
explained thoroughly
in
Section
9.5.1.
For
now,
we
will
content ourselves with
a
qualitative description
of
this relationship.
A
"rough"
function
(one
that
varies rapidly with
x]
must have
a lot of
high
frequency
content (because high
frequency
modes—sin
(rnrx/l)
with
n
large—change
rapidly with
x), and
therefore
the
Fourier
coefficients
must decay
to
zero
slowly
as n
-»
oo.
On the
other hand,
a
smooth
function,
one
that
changes
slowly
with
x,
must
be
made
up
mostly
of low
frequency waves,
and so the
Fourier
coefficients
decay rapidly with
x.
For
example,
a
function with
a
discontinuity
is
"rough"
in the
sense
that
we
are
discussing,
and its
Fourier
coefficients
go to
zero only
as
fast
as
1/n.
A
function
that
is
continuous
but
whose derivative
is
discontinuous
has
Fourier
coefficients
that
decay
to
zero like
1/n
2
(assuming
the
function
satisfies
the
same boundary conditions
as the
eigenfunctions). This pattern continues:
Each additional degree
of
smoothness
in the
function corresponds
to an
addi-
tional factor
of n in the
denominator
of the
Fourier
coefficients.
For
examples,
the
reader
is
referred
to
Exercise
13
and,
for a
complete explanation,
to
Section
9.5.1.
The
fact
that
the
solution
u(x,
t}
of the
homogeneous heat equation
is
very
smooth
can be
understood physically
as
follows:
If
somehow
a
temperature
distribution
that
has a lot of
high
frequency
content (meaning
that
the
tem-
perature
changes rapidly with
x) is
induced,
and
then
the
temperature
dis-
tribution
is
allowed
to
evolve without external
influence,
the
heat
energy
will
quickly
flow
from
high temperature regions
to low
temperature regions
and
smooth
out the
temperature distribution.
2.
For
each
fixed n, the
Fourier
coefficient
a
n
(t)
decays exponentially
as t
—>•
oo.
Moreover,
the
rate
of
decay
is
faster
for
larger
n.
This
is
another implication
of
the
fact
that
the
temperature distribution
u
becomes smoother
as t
increases,
and
means
that,
as t
grows,
fewer
and
fewer
terms
in the
Fourier series
are
required
to
produce
an
accurate approximation
to the
solution
u(x,t}.
When
t is
large
enough,
the first
term from
the
Fourier series provides
an
excellent
approximation
to the
solution.
As
an
illustration
of
this,
we
graph,
in
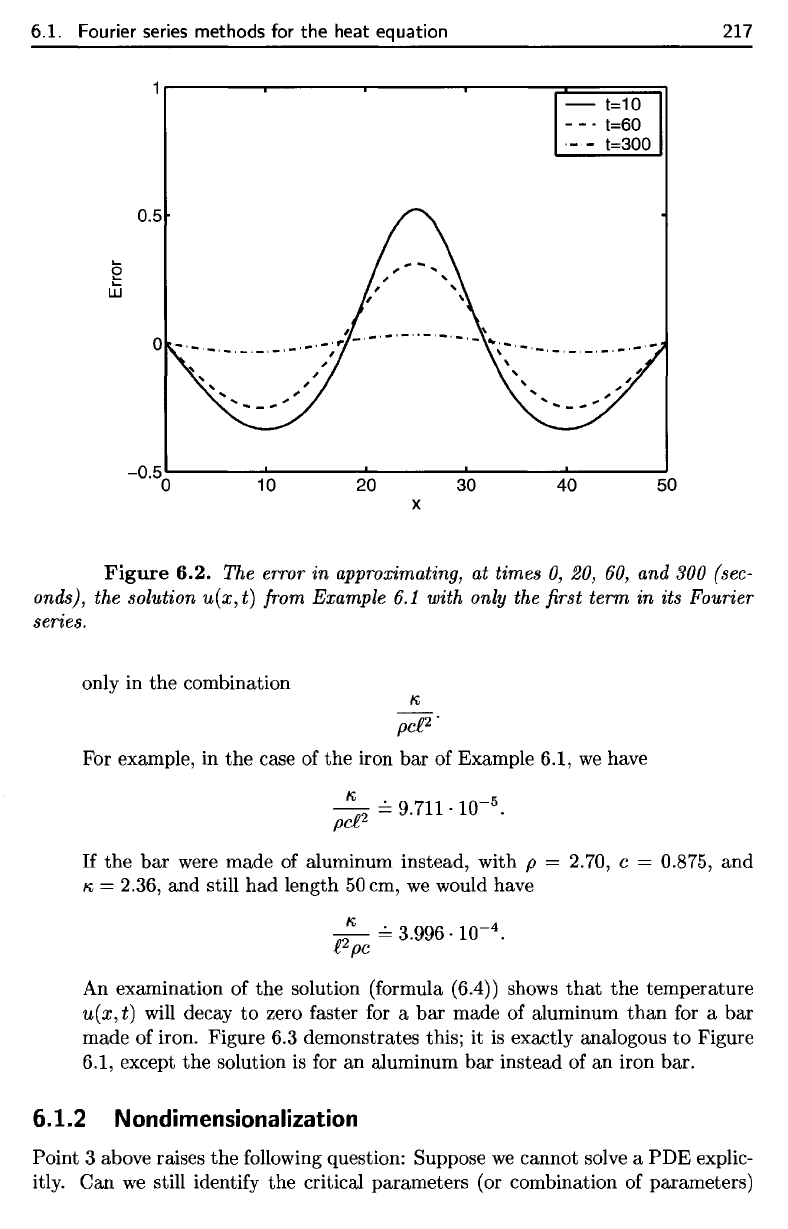
Figure 6.2,
the
difference
between
u(x,
t) and the first
term
of its
Fourier series
for t = 10, t = 20, and t =
300.
(We
used
10
terms
of the
Fourier series
to
approximate
the
exact solution.
Figure
6.2
suggests
that
this
is
plenty.)
3. The
material characteristics
of the bar
appear
in the
formula
for the
solution
216 Chapter
6.
Heat
flow
and diffusion
This can be seen in Figure 6.1;
at
t =
0,
the temperature distribution has a
singularity (a point of nondifferentiability)
at
x =
25.
This singularity
is
not
seen even after 10 seconds.
In
fact, it can be shown mathematically
that
the
solution
u(x,
t)
is
infinitely differentiable as a function of x for every t >
0,
and this holds for every initial temperature distribution
'ljJ
E
e[o,
fl.
The
relationship between
the
smoothness of a function and
the
rate
of decay
of its Fourier will be explained thoroughly in Section 9.5.1. For now,
we
will
content ourselves with a qualitative description of this relationship. A "rough"
function (one
that
varies rapidly with
x)
must have a lot of high frequency
content (because high frequency
modes-sin
(mrx /
f)
with n
large-change
rapidly with x), and therefore
the
Fourier coefficients must decay to zero
slowly as n
-t
00.
On the other hand, a smooth function, one
that
changes
slowly with
x, must be made up mostly of
low
frequency waves, and so the
Fourier coefficients decay rapidly with
x.
For example, a function with a discontinuity
is
"rough" in
the
sense
that
we
are discussing, and its Fourier coefficients
go
to
zero only as fast as
lin.
A
function
that
is
continuous
but
whose derivative
is
discontinuous has Fourier
coefficients
that
decay
to
zero like
1/n
2
(assuming the function satisfies the
same boundary conditions as the eigenfunctions). This
pattern
continues:
Each additional degree of smoothness in the function corresponds to
an
addi-
tional factor of
n in the denominator of
the
Fourier coefficients. For examples,
the
reader
is
referred
to
Exercise 13 and, for a complete explanation, to Section
9.5.1.
The
fact
that
the solution
u(x,
t) of the homogeneous heat equation
is
very
smooth can be understood physically as follows:
If
somehow a temperature
distribution
that
has a lot of high frequency content (meaning
that
the tem-
perature changes rapidly with
x)
is
induced, and then the temperature dis-
tribution
is
allowed to evolve without external influence, the heat energy will
quickly
flow
from high temperature regions to
low
temperature regions
and
smooth out the temperature distribution.
2.
For each fixed n, the Fourier coefficient an(t) decays exponentially as t
-t
00.
Moreover, the
rate
of decay
is
faster for larger n. This
is
another implication of
the fact
that
the
temperature distribution u becomes smoother as t increases,
and means
that,
as t grows, fewer and fewer terms in the Fourier series are
required
to
produce
an
accurate approximation
to
the solution
u(x,
t).
W'hen
t is large enough, the first term from the Fourier series provides an excellent
approximation to the solution.
As
an
illustration of this,
we
graph, in Figure 6.2, the difference between
u(x,
t) and the first term of its Fourier series for t = 10, t =
20,
and t = 300.
(We
used
10
terms of the Fourier series to approximate the exact solution.
Figure 6.2 suggests
that
this
is
plenty.)
3.
The
material characteristics of the
bar
appear in the formula for the solution
6.1. Fourier
series
methods
for the
heat equation
217
Figure
6.2.
The
error
in
approximating,
at
times
0, 20, 60, and 300
(sec-
onds),
the
solution
u(x,t)
from Example
6.1
with
only
the first
term
in its
Fourier
series.
onlv
in the
combination
An
examination
of the
solution
(formula
(6.4))
shows
that
the
temperature
u(x,t)
will
decay
to
zero faster
for a bar
made
of
aluminum
than
for a bar
made
of
iron. Figure
6.3
demonstrates this;
it is
exactly analogous
to
Figure
6.1,
except
the
solution
is for an
aluminum
bar
instead
of an
iron bar.
6.1.2
Nondimensionalization
Point
3
above raises
the
following
question: Suppose
we
cannot solve
a PDE
explic-
itly.
Can we
still
identify
the
critical parameters
(or
combination
of
parameters)
For
example,
in the
case
of the
iron
bar of
Example
6.1,
we
have
If
the bar
were made
of
aluminum instead, with
p —
2.70,
c =
0.875,
and
K
=
2.36,
and
still
had
length
50cm,
we
would
have
6.1. Fourier
series
methods for the heat equation
...
e
W
10
20
x
217
- t=10
-
_.
t=60
.-
- t=300
30
40
50
Figure
6.2.
The error in approximating, at times
0,
20,
60,
and 300 (sec-
onds), the solution
u(x,
t) from Example 6.1 with only the first term in its Fourier
series.
only in
the
combination
",
pC£2·
For example, in
the
case of
the
iron
bar
of Example 6.1,
we
have
If
the
bar
were made of aluminum instead, with p = 2.70, c = 0.875,
and
",
= 2.36,
and
still
had
length
50
cm,
we
would have
02'"
~
3.996 .
10-
4
.
1;
pc
An examination of
the
solution (formula (6.4)) shows
that
the
temperature
u(x,
t) will decay
to
zero faster for a
bar
made of aluminum
than
for a
bar
made of iron. Figure 6.3 demonstrates this;
it
is exactly analogous
to
Figure
6.1, except
the
solution is for
an
aluminum
bar
instead of
an
iron bar.
6.1.2 Nondimensionalization
Point 3 above raises
the
following question: Suppose
we
cannot solve a
PDE
explic-
itly. Can
we
still identify
the
critical parameters (or combination of parameters)
