Gockenbach M.S. Partial Differential Equations. Analytical and Numerical Methods
Подождите немного. Документ загружается.

218
Chapter
6.
Heat flow
and
diffusion
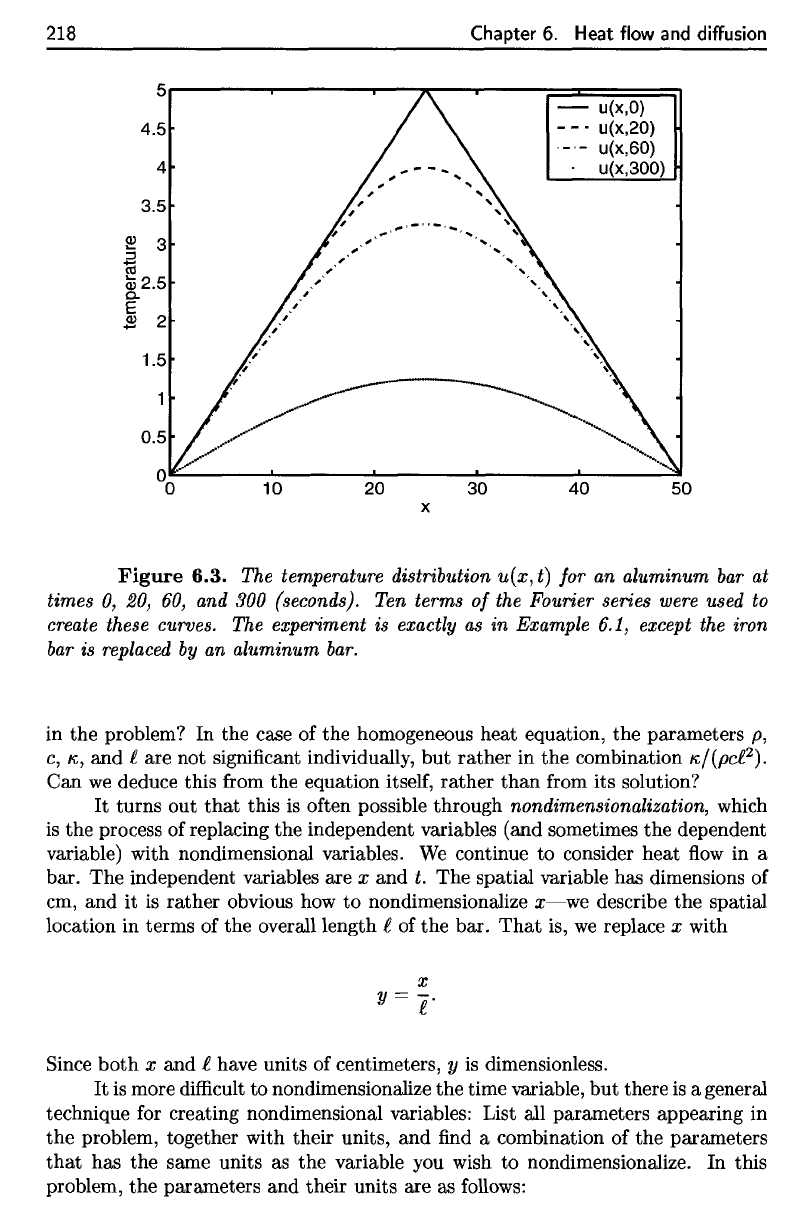
Figure
6.3.
The
temperature distribution
u(x,t)
for an
aluminum
bar at
times
0, 20, 60, and 300
(seconds).
Ten
terms
of the
Fourier series
were
used
to
create
these curves.
The
experiment
is
exactly
as in
Example
6.1,
except
the
iron
bar
is
replaced
by an
aluminum bar.
in
the
problem?
In the
case
of the
homogeneous heat equation,
the
parameters
p,
c,
K,
and t are not
significant individually,
but
rather
in the
combination
K/(pcl
2
).
Can we
deduce this
from
the
equation
itself,
rather than
from
its
solution?
It
turns
out
that
this
is
often
possible through
nondimensionalization,
which
is
the
process
of
replacing
the
independent variables (and sometimes
the
dependent
variable) with
nondimensional
variables.
We
continue
to
consider heat
flow in a
bar.
The
independent variables
are x and t. The
spatial variable
has
dimensions
of
cm,
and it is
rather obvious
how to
nondimensionalize
x—we
describe
the
spatial
location
in
terms
of the
overall
length
t of the
bar.
That
is, we
replace
x
with
Since
both
x and t
have units
of
centimeters,
y is
dimensionless.
It is
more
difficult
to
nondimensionalize
the
time variable,
but
there
is a
general
technique
for
creating nondimensional variables: List
all
parameters appearing
in
the
problem, together with their units,
and find a
combination
of the
parameters
that
has the
same units
as the
variable
you
wish
to
nondimensionalize.
In
this
problem,
the
parameters
and
their
units
are as
follows:
218
Chapter
6.
Heat flow
and
diffusion
5r-----~----~--~--~--_r====~~
u(x,O)
4.5
4
3.5
~
3
::J
<ii
0;2.5
0-
E
.sa
2
1.5
10
20
30
x
40
u(x,20)
u(x,60)
u(x,300)
50
Figure
6.3.
The temperature distribution u(x, t) for an aluminum
bar
at
times
0,
20,
60,
and 300 (seconds). Ten terms
of
the Fourier series were used to
create these curves. The experiment is exactly
as
in Example 6.1, except the iron
bar
is
replaced
by
an aluminum
bar.
in the problem? In the case of the homogeneous heat equation, the parameters
p,
c,
tr"
and
l are not significant individually,
but
rather in the combination
tr,/(pC£2).
Can
we
deduce this from the equation itself, rather
than
from its solution?
It
turns out
that
this
is
often possible through nondimensionalization, which
is
the process of replacing the independent variables (and sometimes the dependent
variable) with nondimensional variables.
We
continue to consider heat
flow
in a
bar. The independent variables are
x and
t.
The spatial variable has dimensions of
cm,
and
it
is
rather obvious how
to
nondimensionalize
x-we
describe the spatial
location in terms of the overall length
l of
the
bar.
That
is,
we
replace x with
x
y=
e·
Since
both
x and l have units of centimeters, y
is
dimensionless.
It
is
more difficult to nondimensionalize the time variable,
but
there
is
a general
technique for creating nondimensional variables: List all parameters appearing in
the
problem, together with their units, and find a combination of
the
parameters
that
has
the
same units as the variable you wish
to
nondimensionalize. In this
problem,
the
parameters and their units are as follows:

6.1. Fourier
series
methods
for the
heat equation
219
Then
the
ratio
is
seen
to
have units
of
seconds,
so we
define
a
dimensionless time variable
s by
Then,
by the
chain
rule,
and
Therefore,
the PDE
is
equivalent
to
which
simplifies
to
We
then
define
v(y,s)
=
u(x,t),
where
(y,s)
and
(x,t)
are
related
by
parameter
P
c
K
t
units
g/cm
3
J/(gK)
J/(scmK)
cm
6.1. Fourier
series
methods for the heat equation
Then
the
ratio
parameter units
p
g/cm
3
c
J/(gK)
'"
J/(s
cmK)
"
pd
2
'"
cm
219
is
seen
to
have units of seconds,
so
we
define a dimensionless time variable s by
t ",t
s=--=--.
pd
2
/",
pd
2
We
then define v(y,
s)
= u(x, t), where
(y,
s)
and
(x,
t) are related by
Then, by the chain rule,
and
Therefore, the
PDE
is
equivalent
to
which simplifies
to
x ",t
Y =
e'
s =
pd
2 •
AU
avos
at
as
at

The
Fourier sine
coefficients
of
if)(ly),
considered
as a
function
of y on the
interval
[0,1],
are the
same
as the
Fourier sine
coefficients
of
i})(x)
as a
function
of x on the
interval
[0,1]
(see Exercise
6).
What
did we
gain
from
nondimensionalization?
We
identified
the
natural
time scale, namely,
pcl
2
/K,
for the
experiment,
and we did
this without solving
the
equation. Whether
we
have
an
iron
or
aluminum bar,
the
problem
can be
written
as
(6.5). This shows
that
the
evolution
of the
temperature
will
be
exactly
the
same
for the two
bars, except
that
the
temperature evolves
on
different
time
scales, depending
on the
material
properties
of the
bars.
Moreover,
we see
exactly
how
this time scale depends
on the
various parameters,
and
this
can
give some
information
that
is not
immediately obvious
from
the
equation.
For
example,
it
is
obvious
from
the
equation
that,
holding
p
constant,
a bar
with
specific
heat
c
and
thermal conductivity
K
will
behave
the
same
as a bar
with
specific
heat
2c and
thermal conductivity
2«.
However,
it is not at all
obvious
that,
holding
p and c
constant,
a bar of
length
t
with thermal conductivity
K
will
behave just
as a bar of
length
21
with thermal conductivity
4«.
35
220
Chapter
6.
Heat
flow
and
diffusion
Since
x =
iy
and x
—
t
corresponds
to y = 1, the
IBVP
(6.1), with
f(x,
t) = 0,
becomes
where
s
0
=
Kt
0
/(pcl
2
).
The
solution
of
(6.5)
is
computed
as
above;
the
result
is
6.1.3
The
inhomogeneous
heat
equation
We
now
consider
an
inhomogeneous problem.
Example
6.2.
The
diffusion coefficient
for
carbon
monoxide (CO)
in air is D =
0.208cm
2
/s.
We
consider
a
pipe
of
length
100cm,
filled
with air, that initially
contains
no CO. We
assume that
the two
ends
of
the
pipe
open
onto
large
reservoirs
of
air,
also
containing
no CO, and
that
CO is
produced
inside
the
pipe
at a
constant
rate
of
10~
7
g/cm
3
per
second.
We
write
u(x,
t},
0 < x <
100,
for the
concentration
of
CO in
air,
in
units
of
g/cm
3
,
and
model
u as the
solution
of
the
IBVP
35
For
a
thorough discussion
of
nondimensionalization
and
scale models,
see
[36],
Chapter
6.
220
Chapter
6.
Heat flow
and
diffusion
Since x =
£y
and
x = £ corresponds
to
y = 1,
the
IBVP
(6.1), with
f(x,
t) = 0,
becomes
av
a
2
v
as
- ay2 = 0,
0<
y <
1,
s > so,
v(y, so) =
'ljJ(£y),
0<
y <
1,
v(O,s) = 0, s > so,
v(1,s)
=0,
s > so,
(6.5)
where
So
=
/'1,tO/(pC£2).
The
solution of (6.5) is computed
as
above;
the
result is
00
v(s,
y)
= L
bne-n27r2S
sin (mry).
n=l
The
Fourier sine coefficients of
'ljJ(£y)
, considered
as
a function
of
yon
the
interval
[0,1]' are
the
same as
the
Fourier sine coefficients of'ljJ(x) as a function
of
x on
the
interval
[0,
£]
(see Exercise 6).
What
did
we
gain from nondimensionalization?
We
identified
the
natural
time scale, namely,
pC£2
/
/'1"
for
the
experiment,
and
we
did this without solving
the
equation.
Whether
we
have
an
iron
or
aluminum bar,
the
problem can
be
written as (6.5). This shows
that
the
evolution
of
the
temperature
will be exactly
the
same for
the
two bars, except
that
the
temperature
evolves
on
different time
scales, depending
on
the
material properties of
the
bars. Moreover,
we
see exactly
how this time scale depends
on
the
various parameters,
and
this can give some
information
that
is not immediately obvious from
the
equation. For example, it
is obvious from
the
equation
that,
holding p constant, a
bar
with specific heat c
and
thermal
conductivity
/'1,
will behave
the
same
as
a
bar
with specific
heat
2c
and
thermal
conductivity
2/'1,.
However,
it
is
not
at
all obvious
that,
holding p
and
c
constant, a
bar
of length £ with
thermal
conductivity
/'1,
will behave
just
as
a
bar
of
length
2£
with thermal conductivity
4/'1,.35
6.1.3
The
inhomogeneous heat equation
We
now consider
an
inhomogeneous problem.
Example
6.2.
The diffusion coefficient for carbon monoxide (CO) in air is D =
0.208cm2 /
s.
We consider a pipe
of
length 100 cm, filled with air, that initially
contains no CO. We assume that the two ends
of
the pipe open onto large reservoirs
of
air, also containing no
CO,
and that
CO
is produced inside the pipe at a constant
rate
of
10-
7
g/
cm
3
per second. We write
u(x,
t),
0 < x < 100, for the concentration
of
co
in
air,
in
units
of
g/
cm
3
,
and model u
as
the solution
of
the
IEVP
au
a
2
u
-7
at - D ax
2
=
10
,0
< x <
100,
t >
0,
u(x,O) =
0,
0 < x <
100,
35For a
thorough
discussion
of
nondimensionalization
and
scale models, see
[36],
Chapter
6.

6.1.
Fourier
series
methods
for the
heat equation
221
We
wish
to
determine
the
evolution
of the
concentration
of
CO in the
pipe.
We
write
the
solution
u in the
form
so
that
Using
(6.3),
we
obtain
To
find the
coefficients
a
n
(t)
of
u(x,t),
we
must
solve
the
IVPs
where
We
have
In
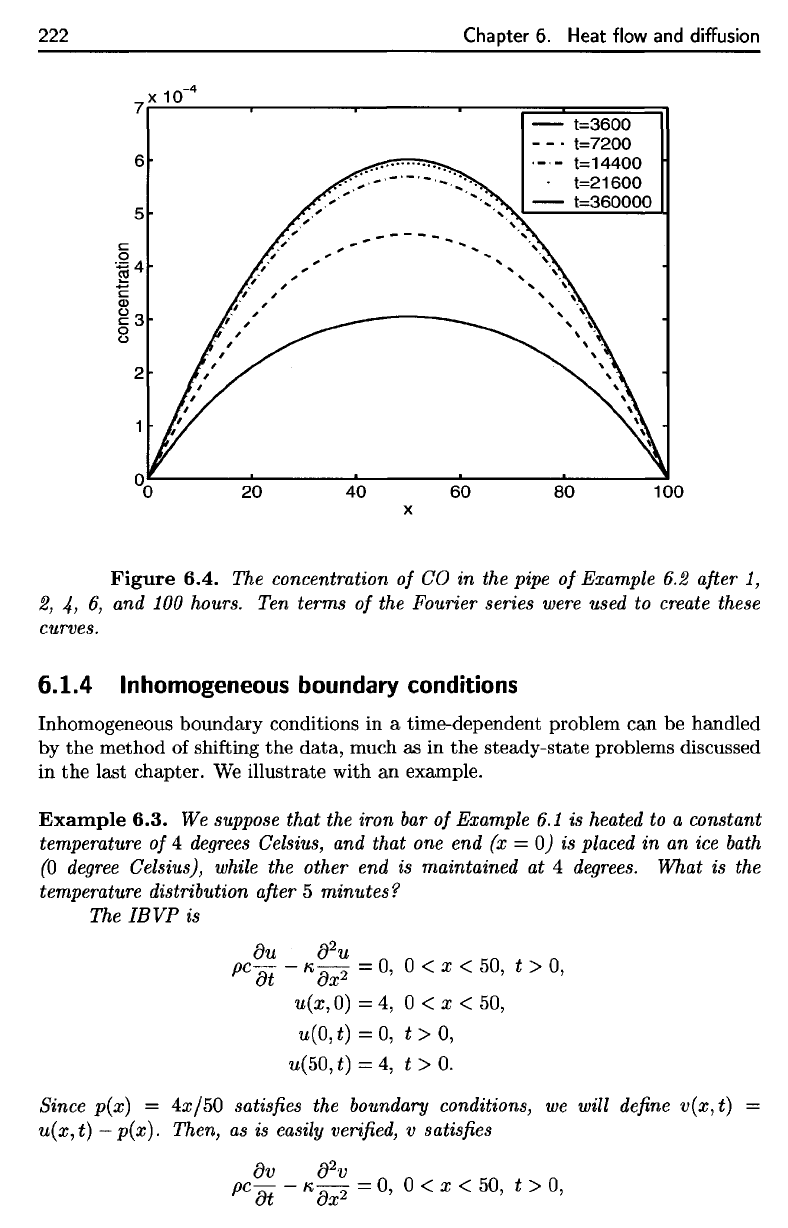
Figure
6.4,
we
show
the
concentration
of CO in the
pipe
at
times
t =
3600
(1
hour),
t =
7200
(2
hours),
t =
14400
(4
hours),
t =
21600
(6
hours),
andt
=
360000
(100
hours).
The
graph
suggests that
the
concentration
approaches
steady
state
(the
reader
should notice
how
little
the
concentration changes between
4
hours
and 100
hours
of
elapsed
time).
We
discuss
the
approach
to
steady
state
below
in
Section
6.1.5.
6.1. Fourier series methods for
the
heat equation
u(O,
t) = 0, t > 0,
u(100, t) =
0,
t >
O.
We wish to determine the evolution
of
the concentration
of
CO
in
the pipe.
We write the solution u
in
the
form
00
u(x,
t) = L an(t) sin
(~~~),
n=l
so
that
We have
-7
~
.
(mrx)
10
=
~
C
n
sm 100 '
n=l
where
2
(IOO
_ . mrx
2.1O-
7
(1-(-1)n)
en
= 100
io
10
7 sm (
100)
dx
= mr ' n =
1,2,3,
....
To
find the coefficients an(t)
of
u(x,
t),
we
must
solve the
IVPs
dan
Dn
2
Jr2
dt +
1002
an
= c
n
,
an(O)
=
o.
Using (6.3), we obtain
221
In
Figure
6.4,
we
show the concentration
of
CO
in
the pipe at
times
t = 3600
(1
hour), t = 7200 (2 hours), t = 14400
(4
hours), t = 21600 (6 hours),
andt
= 360000
(100 hours). The graph suggests
that
the concentration approaches steady state (the
reader should notice how little the concentration changes between
4 hours and 100
hours
of
elapsed
time).
We discuss the approach to steady state below
in
Section
6.1.5.
222
Chapter
6.
Heat
flow
and
diffusion
Figure
6.4.
The
concentration
of CO in the
pipe
of
Example
6.2
after
1,
2, 4, 6, and 100
hours.
Ten
terms
of the
Fourier series
were
used
to
create these
curves.
6.1.4
In
homogeneous boundary conditions
Inhomogeneous
boundary conditions
in a
time-dependent problem
can be
handled
by
the
method
of
shifting
the
data,
much
as in the
steady-state
problems discussed
in
the
last
chapter.
We
illustrate with
an
example.
Example
6.3.
We
suppose
that
the
iron
bar
of
Example
6.1 is
heated
to a
constant
temperature
of
4
degrees
Celsius,
and
that
one end (x
=
0)
is
placed
in an ice
bath
(0
degree
Celsius),
while
the
other
end is
maintained
at 4
degrees.
What
is the
temperature
distribution
after
5
minutes
?
The
IBVP
is
Since p(x)
=
4#/50
satisfies
the
boundary
conditions,
we
will
define
v(x,t)
=
u(x,t)
—
p(x).
Then,
as is
easily
verified,
v
satisfies
222
6
5
2
20
Chapter
6.
Heat flow
and
diffusion
-----
.......
40
60
x
-
t=3600
-
_.
t=7200
._.-
t=14400
t=21600
-
t=360000
80
100
Figure
6.4.
The concentration
of
co
in
the pipe
of
Example 6.2 after 1,
2,
4,
6,
and
100 hours. Ten
terms
of
the Fourier series were used
to
create these
curves.
6.1.4 Inhomogeneous boundary conditions
Inhomogeneous
boundary
conditions in a time-dependent problem can be handled
by
the
method of shifting
the
data,
much as in
the
steady-state problems discussed
in
the
last chapter.
We
illustrate with
an
example.
Example
6.3.
We
suppose
that
the iron bar
of
Example 6.1 is heated to a
constant
temperature
of
4 degrees Celsius,
and
that
one
end
(x
=
O)
is placed
in
an
ice bath
(0
degree Celsius), while the other end is
maintained
at
4 degrees.
What
is the
temperature distribution after 5 minutes'?
The
IEVP
is
{)u
{)2u
pc
{)t
- K, {)x
2
=
0,
0 < x < 50, t > 0,
u(x,O)
=
4,
0 < x < 50,
u(O,
t)
=
0,
t > 0,
u(50,
t)
=
4,
t >
O.
Since
p(x)
=
4x/50
satisfies the boundary conditions, we will define
v(x,
t)
=
u(x,t)
-
p(x).
Then, as
is
easily verified, v satisfies
{)v
{)2v
pc
{)t
- K, {)x
2
= 0, 0 < x < 50, t > 0,

where
is
determined
by the
IVPs
6.1. Fourier
series
methods
for the
heat equation
223
The
initial temperature
satisfies
The
solution
so the
solution
is
The
solution
u
is
then given
by
The
temperature distribution
at t = 300 is
shown
in
Figure
6.5.
In
a
time-dependent problem,
inhomogeneous
boundary conditions
can
them-
selves
be
time dependent;
for
example,
are
valid inhomogeneous Dirichlet conditions.
The
function
satisfies
these conditions.
The
reader should notice
that
the
function
v(x,i)
=
u(x,
t)
—p(x,
t]
will
not
satisfy
the
same
PDE as
does
w;
the
right-hand side
will
be
different.
See
Exercise
5.
6.1. Fourier
series
methods for the heat equation
4
v(x,O) = 4 -
50x,
0<
x < 50,
v(O,
t) = 0, t > 0,
v(50, t) = 0, t >
O.
The initial temperature satisfies
where
The solution
4 L
oo
.
(nnx)
4-
-x=
b sm
--
50
n
50'
n=l
8
b
n
=
-,
n =
1,2,3,
....
nn
00
v(x,
t) = L an(t) sin
(n;x)
n=l
is determined
by
the
IVPs
dan
K,n
2
n
2
dt
+
pc502
an
= 0,
an(O)
= b
n
,
so the solution is
00
8 _
«n
2
,,2
t
nnx
v(x,t)
= L
-e
~
sin
(-).
nn
50
n=l
The solution u is then given
by
4
00
8
_"n
2
..
2
t
nnx
u(x,
t) =
-x
+ L
-e
pc50
2
sin
(-).
50
n=l
nn
50
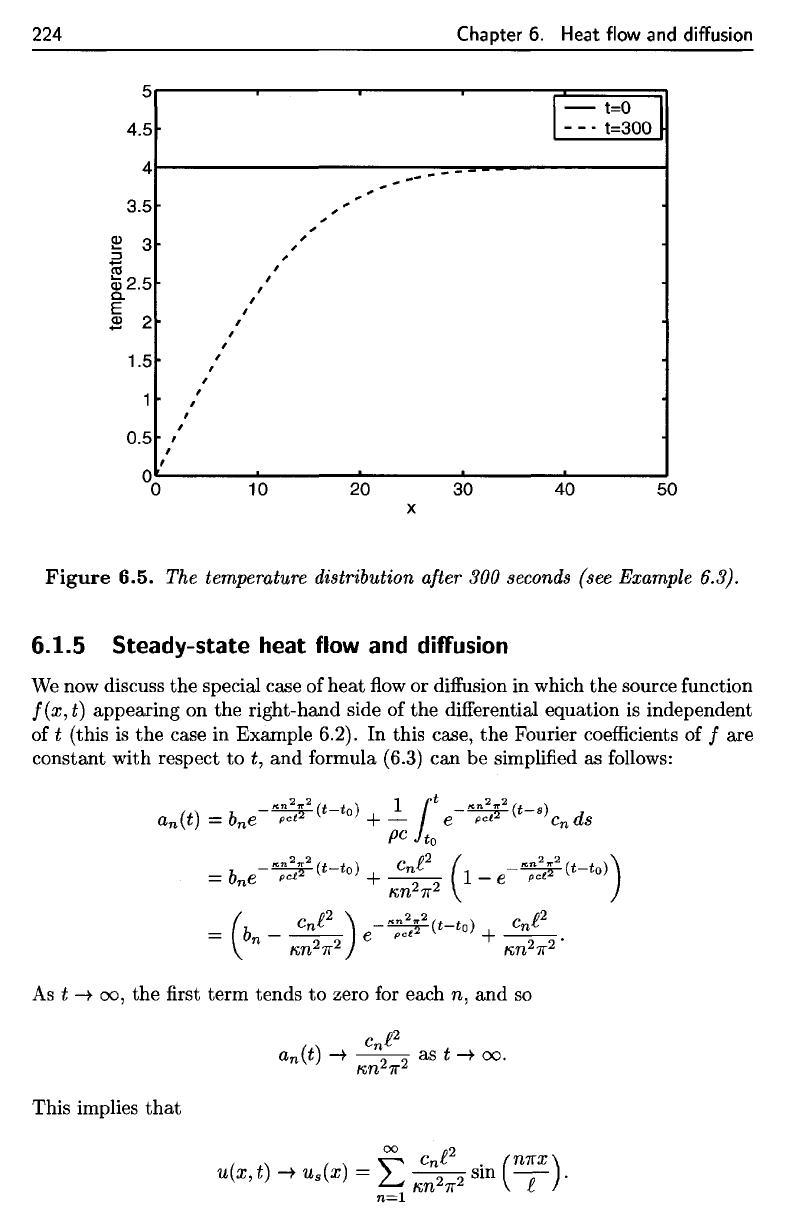
The temperature distribution at t = 300 is shown in Figure 6.5.
223
In a time-dependent problem, inhomogeneous
boundary
conditions can them-
selves be time dependent; for example,
u(O,
t) = g(t), u(£, t) =
h(t),
t > 0,
are valid inhomogeneous Dirichlet conditions.
The
function
x
p(x, t) = g(t) + C(h(t) - g(t))
satisfies these conditions.
The
reader should notice
that
the
function
v(x,
t)
u(x,
t) - p(x, t) will not satisfy
the
same
PDE
as does u;
the
right-hand side will
be
different. See Exercise
5.
224
Chapter
6.
Heat flow
and
diffusion
Figure
6.5.
The
temperature distribution
after
300
seconds
(see
Example
6.3).
6.1.5 Steady-state heat flow
and
diffusion
We
now
discuss
the
special case
of
heat
flow or
diffusion
in
which
the
source function
/(#,£)
appearing
on the
right-hand side
of the
differential
equation
is
independent
of
t
(this
is the
case
in
Example 6.2).
In
this case,
the
Fourier
coefficients
of / are
constant with respect
to t, and
formula
(6.3)
can be
simplified
as
follows:
This implies
that
As
t
—>•
oo,
the first
term tends
to
zero
for
each
n,
and so
224
5
4.5
4
3.5
~
3
:::J
~
(1)2.5
c..
E
2
2
1.5
0.5
I
I
I
00
I
I
I
I
I
I
I
I
I
I
I
I
,
,
10
,
I
,
,
,
..
..
,
-
--
20
x
Chapter
6.
Heat flow
and
diffusion
---
30
1
-
t-O
I
-
_.
t=300
~
40
50
Figure
6.5. The temperature distribution after 300 seconds (see Example 6.3).
6.1.5 Steady-state heat flow and diffusion
We
now discuss the special case of
heat
flow
or diffusion in which the source function
f(x,
t) appearing on the right-hand side of the differential equation
is
independent
of
t (this
is
the
case in Example 6.2).
In
this case,
the
Fourier coefficients of f are
constant with respect
to
t, and formula (6.3) can be simplified as follows:
As
t
-+
00,
the first term tends
to
zero for each n,
and
so
This implies
that
00
£2
u(x,t)
-+
Us(x) = L
",~27f2
sin
(n;x).
n=l

6.1. Fourier
series
methods
for the
heat
equation
225
The
limit
u
s
(x)
is the
steady-state temperature distribution.
It is not
difficult
to
show
that
u
s
is the
solution
to the BVP
(see
Exercise
2). It
should
be
noted
that
the
initial temperature distribution
is
irrelevant
in
determining
the
steady-state temperature distribution.
Similar
results hold
for the
diffusion
equation, which
is
really
no
different
from
the
heat
equation except
in the
meaning
of the
parameters. Indeed, Example
6.2
is
an
illustration;
the
concentration
u
approaches
a
steady-state concentration,
as
suggested
by
Figure
6.4
(see Exercise
1).
In the
next section,
we
will
turn
our
attention
to two new
sets
of
boundary
conditions
for the
heat
equation
and
derive Fourier series methods
that
apply
to
the new
boundary conditions. First, however,
we
briefly
discuss another derivation
of
the
Fourier series method.
6.1.6 Separation
of
variables
There
is
another
way to
derive Fourier series solutions
of the
heat equation,
which
is
called
the
method
of
separation
of
variables.
It is in
some ways more elementary
than
the
point
of
view
we
have presented,
but it is
less general.
To
introduce
the
method
of
separation
of
variables,
we
will
use the
following
IBVP:
The
reader should notice
that
the PDE is
homogeneous; this
is
necessary
and a
significant
limitation
of
this
technique.
Here
is the key
idea
of the
method
of
separation
of
variables:
we
look
for
separated
solutions:
u(x,
t) =
X(x)T(t)
(X and T are
functions
of a
single
variable).
Substituting;
u
into
the PDE
vields
6.1. Fourier
series
methods for the heat equation
225
The
limit us(x)
is
the steady-state temperature distribution.
It
is
not difficult
to
show
that
Us
is
the
solution
to
the
BVP
cPU
-r;,
daP
=
f(x),
0 < x <
f,
u(O) = 0,
(6.6)
u(f)
= 0
(see Exercise
2).
It
should be noted
that
the initial temperature distribution
is
irrelevant in determining the steady-state temperature distribution.
Similar results hold for
the
diffusion equation, which
is
really no different from
the heat equation except in the meaning of
the
parameters. Indeed, Example 6.2
is
an
illustration; the concentration u approaches a steady-state concentration, as
suggested by Figure
6.4 (see Exercise 1).
In
the
next section,
we
will
turn
our attention
to
two new sets of boundary
conditions for the
heat
equation and derive Fourier series methods
that
apply
to
the new boundary conditions. First, however,
we
briefly discuss another derivation
of the Fourier series method.
6.1.6 Separation of
variables
There
is
another way
to
derive Fourier series solutions of
the
heat equation, which
is
called the method of separation
of
variables.
It
is in some ways more elementary
than
the
point of view
we
have presented,
but
it
is
less general.
To introduce the method of separation of variables,
we
will use the following
IBVP:
{)u
{)2u
pc
{)t
-
r;,
{)x
2
=
0,
0 < x <
f,
t > to,
u(x, to) =
'l/J(x),
0 < x <
f,
u(O,
t)
= 0, t > to,
u(f,
t)
= 0, t > to.
(6.7)
The reader should notice
that
the
PDE
is
homogeneous; this
is
necessary and a
significant limitation of this technique.
Here
is
the key idea of the method of separation of variables:
we
look for
separated solutions:
u(x,
t) =
X(x)T(t)
(X
and T are functions of a single variable).
Substituting u into
the
PDE
yields
{)u
{)2U
U =
XT,
pc
{)t
-
r;,
{)x
2
= 0
dT
d
2
X
=>
pcX-
-
r;,T--
= 0
dt dx
2
cP
X
dT
=>
-r;,T--
=
-pcX-
dx
2
dt
_ld
2
X
_ldT
=>
-r;,X
d,x2
=
-peT
di·

226
Chapter
6.
Heat
flow
and
diffusion
The
last
step
follows
upon dividing both sides
of the
equation
by XT. The
crucial
observation
is the
following:
is
a
function
of x
alone, while
is
a
function
of t
alone.
The
only
way
these
two
functions
can be
equal
is if
they
are
both constants:
We
now
have ODEs
for
X(x)
and
T(t)
Moreover,
the
boundary conditions
for
u
imply boundary conditions
for
X:
(the function
T(t)
cannot
be
zero,
for
otherwise
u is the
trivial solution).
We
see
that
the
function
X
must satisfy
the
eigenvalue problem
From
our
earlier work,
we
know
that
there
is a
sequence
of
solutions:
For
each value
of
A
n
,
we can
solve
the ODE
to find a
corresponding function
T
n
:
(b
n
is an
arbitrary
constant).
We
have
now
found
a
sequence
of
separated solutions
to the
homogeneous
heat
equation, namely,
226 Chapter
6.
Heat flow
and
diffusion
The
last step follows upon dividing
both
sides of
the
equation by
XT.
The crucial
observation
is
the following:
is
a function
of
x alone, while
1
dT
-pcT-
dt
is a function of t alone. The only way these two functions can be equal
is
if they
are
both
constants:
-1
J2
X
-1
dT
-liX
dx
2
=
-pcT
dt
=
A.
We
now have ODEs for
X(x)
and T(t):
d
2
X
dT
-Ii
dx
2
= AX,
-pc
dt
=
AT.
Moreover, the boundary conditions for u imply boundary conditions for X:
u(O,
t) = 0
:::}
X(O)T(t) = 0
:::}
X(O) = 0,
u(l,
t) =
O:::}
X(l)T(t)
=
O:::}
X(l)
= 0
(the function
T(t)
cannot be zero, for otherwise u
is
the
trivial solution).
We
see
that
the
function X must satisfy
the
eigenvalue problem
J2x
-Ii
dx
2
= AX, 0 < x <
l,
X(O) = 0,
X(l)
=
O.
From our earlier work,
we
know
that
there
is
a sequence of solutions:
n
2
1f2
(n1fx)
An
=~,
Xn(x) = sin
-l-
, n =
1,2,3,
....
For each value of
An,
we
can solve
the
ODE
dT
-pc-
= AT
dt
to find a corresponding function
Tn:
_
An(t-·o)
Tn(t) =
bne
pc
, n =
1,2,3,
...
(b
n
is
an
arbitrary constant).
We
have now found a sequence of separated solutions to the homogeneous heat
equation, namely,
_"'n(t-to)
•
(n1fX)
un(x,t)=bne
pc
sm
-l-
,n=1,2,3,
....

6.1. Fourier
series
methods
for the
heat equation
227
By
construction, each
of
these
functions
satisfies
the
homogeneous Dirichlet condi-
tions.
To
satisfy
the
initial condition,
we use the
principle
of
superposition
(which
applies because
the
heat equation
is
linear)
to
form
the
solution
then
u(x,to)
=
i^(x]
will
hold.
We
thus
see
that
the
method
of
separation
of
variables yields
the
solution
we
obtained earlier (see Section
6.1.1).
However,
the
method requires
that
the PDE
and
the
boundary conditions
be
homogeneous,
and
this
is a
serious limitation.
For
example,
one
cannot apply separation
of
variables
to a
problem with
inhomogeneous,
time-dependent boundary conditions.
The
method does
not
apply directly,
and one
cannot
use the
trick
of
shifting
the
data,
since
it
would result
in an
inhomogeneous
PDE.
We
will
find
separation
of
variables
useful
in
Section 8.2,
when
we
derive
the
eigenvalues
and
eigenfunctions
for a
differential
operator
defined
on a
rectangle.
We
then have
If
we
choose
61,
b%,
63,...
to be the
Fourier sine
coefficients
of
i/»,
Exercises
1.
What
is the
steady-state
solution
of
Example 6.2? What
BVP
does
it
satisfy?
2.
Find
the
Fourier sine series
of the
solution
of
(6.6)
and
show
that
it
equals
u
8
(x).
3.
Solve
the
following
IBVP
using
the
Fourier series method:
Produce
an
accurate graph
of the
"snapshot"
w(-,0.1).
4.
Solve
the
following
IBVP using
the
Fourier series method:
6.1. Fourier series methods for
the
heat equation
227
By construction, each of these functions satisfies
the
homogeneous Dirichlet condi-
tions.
To satisfy the initial condition,
we
use the principle of superposition (which
applies because the heat equation
is
linear)
to
form the solution
<Xl
~
An(t-tO)
(nnx)
U(X,
t) =
~
bne-
pc
sin -c- .
n=l
We
then
have
<Xl
u(x,
to)
= L b
n
sin
(n;x).
n=l
If
we
choose b
1
,
b
2
,
b
3
,
•••
to
be
the
Fourier sine coefficients of'lj;,
b
n
=
~
1i
'lj;(x) sin
(n;x)
dx,
then
u(x,
to)
= 'lj;(x) will hold.
We
thus see
that
the method of separation of variables yields
the
solution
we
obtained earlier (see Section 6.1.1). However, the method requires
that
the
PDE
and
the
boundary conditions be homogeneous,
and
this
is
a serious limitation. For
example, one cannot apply separation of variables
to
a problem with inhomogeneous,
time-dependent boundary conditions.
The
method does not apply directly, and one
cannot use
the
trick of shifting
the
data,
since
it
would result in
an
inhomogeneous
PDE.
We
will find separation of variables useful in Section 8.2, when
we
derive the
eigenvalues and eigenfunctions for a differential operator defined on a rectangle.
Exercises
1.
What
is
the steady-state solution of Example 6.2?
What
BVP
does
it
satisfy?
2.
Find
the
Fourier sine series of the solution of (6.6) and show
that
it
equals
us(x).
3.
Solve the following IBVP using the Fourier series method:
{)u
fPu
{)t
- {)x2 =
0,
° < x <
1,
t >
0,
u(x,O) = x, ° < x < 1,
u(O,
t) = 0, t >
0,
u(I,
t) = 0, t >
0.
Produce
an
accurate graph of
the
"snapshot" u(·,O.I).
4.
Solve the following IBVP using the Fourier series method:
{)u
{)2u .
{)t - {)x2 = sm (t), ° < x <
1,
t > 0,
