Gockenbach M.S. Partial Differential Equations. Analytical and Numerical Methods
Подождите немного. Документ загружается.


198
Chapter
5.
Boundary value problems
in
statics
new
BVP for the
unknown
w(x)
=
u(x]
—
g(x).
We can
apply this idea
to the
weak
form
of the
BVP.
A
calculation similar
to
that
of
Section 5.4.1 shows
that
the
weak
form
of
(5.55)
is
Here, however,
we do not
look
for the
solution
u in
V,
but
rather
in g + V =
{g
+ v
:
v €
V}.
We now
write
u = g +
w,
and the
problem becomes
But
a(w
+
g,
v) =
a(w,
v) +
a(g,
v),
so we can
write (5.56)
as
It
turns
out
that
solving (5.57)
is not
much harder
than
solving
the
weak formulation
of
the
homogeneous Dirichlet problem;
the
only
difference
is
that
we
modify
the
right-hand-side vector
f,
as we
explain below.
Shifting
the
data
is
easy because
we can
delay
the
choice
of the
function
g
until
we
apply
the
Galerkin
method;
it is
always simple
to find a finite
element function
g
n
which
satisfies
the
boundary conditions
on the
boundary nodes (actually,
for a
one-dimensional problem like
this,
it is
trivial
to find
such
a
function
g in any
case;
however,
this
becomes
difficult
in
higher dimensions, while
finding a finite
element
function
to
satisfy
the
boundary conditions,
at
least
approximately,
is
still easy
in
higher dimensions).
The
Galerkin problem
is:
We
choose
g
n
to be
piece
wise
linear
and
satisfy
g
n
(xo}
= a,
g
n
(x
n
)
=
/3-
the
simplest
such function
has
value zero
at the
other nodes
of the
mesh, namely
g
n
=
afio+ftfin.
Substituting
w
n
=
^ii=i
a
i^i
m
*°
(5-58),
we
obtain,
as
before,
the
linear system
Ku
=
f.
The
matrix
K
does
not
change,
but f
becomes
Example
5.22.
We now
solve
an
inhomogeneous
version
of
Example 5.21;
specif-
i.rnll.ii
IIJP
n.nnln
the
finite
pl.pm.pni.
mpthntt
t.n
198
Chapter
5.
Boundary value problems in statics
new
BVP
for the unknown w(x) = u(x) - g(x).
We
can apply this idea to
the
weak
form of the BVP.
A calculation similar to
that
of Section 5.4.1 shows
that
the weak form of
(5.55)
is
a(u,v) =
(f,v)
for all v E
V.
Here, however,
we
do
not look for the solution u in V,
but
rather in g + V
{g
+ v : v E
V}.
We
now write u = g + w,
and
the
problem becomes
find
wE
V such
that
a(w + g,v) =
(f'v)
for all v E
V.
(5.56)
But
a(w +
g,
v) = a(w, v) + a(g, v),
so
we
can write (5.56) as
find
w E V such
that
a(w,v) =
(f'v)
- a(g,v) for all v E
V.
(5.57)
It
turns out
that
solving (5.57)
is
not much harder
than
solving the weak formulation
of the homogeneous Dirichlet problem; the only difference
is
that
we
modify the
right-hand-side vector
f, as
we
explain below.
Shifting
the
data
is
easy because
we
can delay the choice of the function g until
we
apply
the
Galerkin method; it
is
always simple
to
find a finite element function
gn
which satisfies the boundary conditions on the boundary nodes (actually, for a
one-dimensional problem like this, it
is
trivial
to
find such a function g in any case;
however, this becomes difficult in higher dimensions, while finding a finite element
function
to
satisfy
the
boundary conditions,
at
least approximately,
is
still easy in
higher dimensions).
The Galerkin problem
is:
find
Wn
E
Sn
such
that
a(w
n
,
v)
=
(f,
v)
- a(gn, v) for all v E
Sn-
(5.58)
We
choose
gn
to be piecewise linear
and
satisfy
gn(XO)
=
a,
gn(xn) =
(3;
the simplest
such function has value zero
at
the other nodes
ofthe
mesh, namely
gn
= a¢o+(3¢n.
Substituting
Wn
=
l:~:ll
ai¢i
into (5.58),
we
obtain, as before, the linear system
Ku
=
f.
The matrix K does not change,
but
f becomes
i = 2,3,
...
, n - 2 (since a(gn, ¢i) = 0),
i = 1, (5.59)
i=n-1.
Example
5.22.
We now solve an inhomogeneous version
of
Example 5.21; specif-
ically, we apply the finite element method to
d (
dU)
- dx
(1
+ x) dx (x) =
1,
0 < x <
1,
u(O)
= 2, (5.60)
u(l)
= 1.

5.6.
Piecewise
polynomials
and the
finite
element
method
199
Now,
With
n =
5,
we
obtain
The
results
are
shown
in
Figure
5.17.
In
this case,
the
computed solution
equals
the
exact
solution (the error shown
is
Figure 5.17
is
only
due to
round-off
error
in the
computer calculations) (see Exercise
2).
As we
have
just
explained,
the
approximate solution
is
given
by
where
the
coefficients
iti,
«2,.
•
•,
u
n
-i
satisfy
The
stiffness
matrix
K is
identical
to the one
calculated
in
Example 5.21, while
the
load
vector
f is
modified
as
indicated
in
(5.59).
We
obtain
so
and
5.6. Piecewise polynomials and
the
finite element method 199
As
we have
just
explained, the approximate solution is given by
n-l
Vn(X) = L
UirPi(X),
i=l
where the coefficients
Ul,
U2,
...
,
Un-l
satisfy
Ku=f.
The stiffness
matrix
K is identical to the one calculated in Example 5.21, while the
load vector
f is modified
as
indicated
in
(5.
59}.
We obtain
Now,
i =
2,3,
...
, n - 2 (since a(gn,
rPi)
=
OJ,
i = 1,
i=n-l.
a(rPo,rPd
=
lh
((1
+x)~
(-~))
dx
h+2
2h '
a(rPn,rPn-d =
l~h
((l+X)~
(-~))
dx
so
and
With n
= 5,
we
obtain
h-4
2h'
h+2
II
=h+2----v;-
h-4
fn-l
=
h-
2h"".
r
56/5]
_
1/5
f -
1/5.
97/10
The results are shown
in
Figure 5.17.
In
this case, the computed solution equals the
exact solution (the error shown is Figure
5.17 is only due to round-off error
in
the
computer calculations) (see Exercise
2).
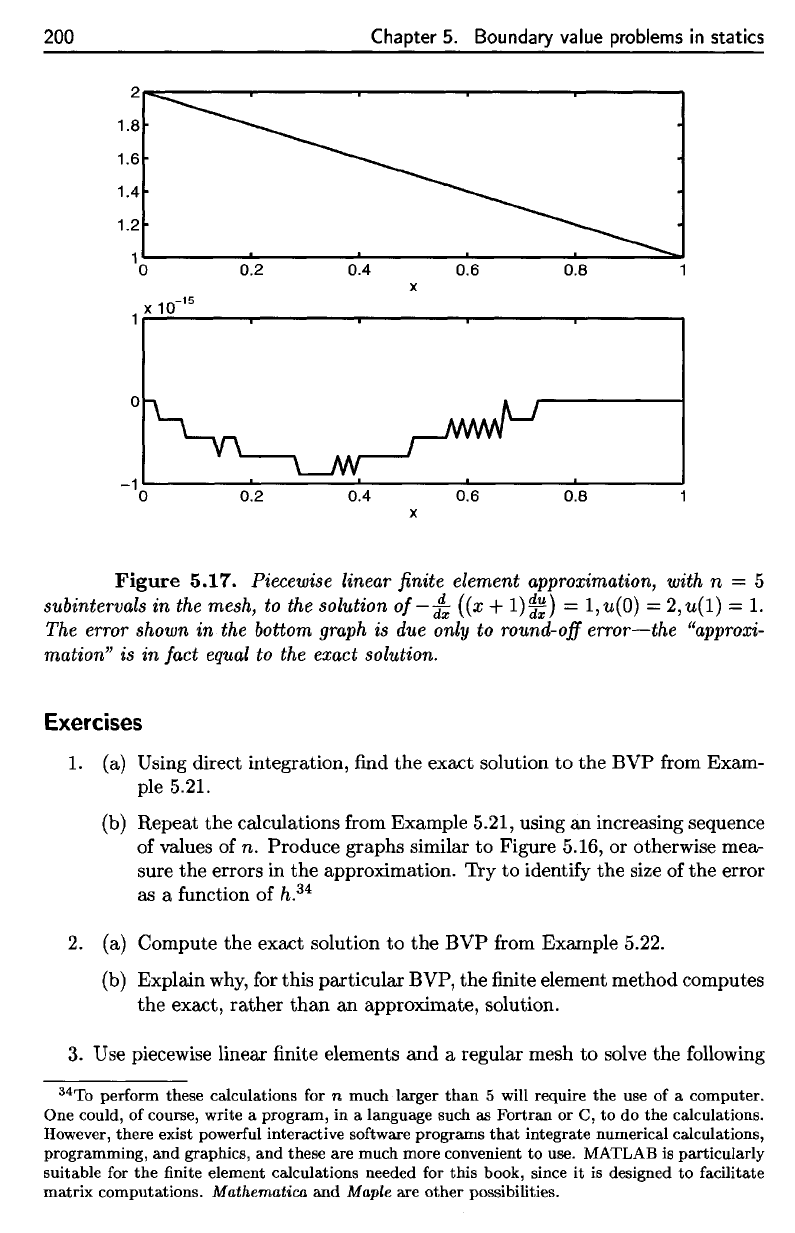
200
Chapter
5.
Boundary value problems
in
statics
Figure
5.17. Piecewise linear
finite
element approximation, with
n
= 5
subintervals
in the
mesh,
to the
solution
of
—
-^
((x +
l)ff)
=
l,w(0)
=
2,w(l)
= 1.
The
error shown
in the
bottom
graph
is due
only
to
round-off
error—the
"approxi-
mation"
is in
fact
equal
to the
exact solution.
Exercises
1. (a)
Using direct integration,
find the
exact
solution
to the BVP
from
Exam-
ple
5.21.
(b)
Repeat
the
calculations
from
Example
5.21, using
an
increasing sequence
of
values
of n.
Produce
graphs
similar
to
Figure 5.16,
or
otherwise mea-
sure
the
errors
in the
approximation.
Try to
identify
the
size
of the
error
as a
function
of
h.
34
2.
(a)
Compute
the
exact
solution
to the BVP
from
Example
5.22.
(b)
Explain why,
for
this particular BVP,
the
finite element method computes
the
exact,
rather
than
an
approximate,
solution.
3. Use
piecewise
linear
finite
elements
and a
regular
mesh
to
solve
the
following
34
To
perform these calculations
for n
much
larger
than
5
will require
the use of a
computer.
One
could,
of
course, write
a
program,
in a
language such
as
Fortran
or C, to do the
calculations.
However,
there exist
powerful
interactive
software
programs that integrate numerical calculations,
programming,
and
graphics,
and
these
are
much more convenient
to
use. MATLAB
is
particularly
suitable
for the finite
element calculations needed
for
this book, since
it is
designed
to
facilitate
matrix
computations.
Mathematica
and
Maple
are
other
possibilities.
200 Chapter
5.
Boundary value problems
in
statics
2~------~--------~--------~------~--------~
1.8
1.6
1.4
1.2
1L-------~~------~--------~--------~------~~
o
0.2
0.4
0.6
0.8
x
0.2 0.8
x
Figure
5.11.
Piecewise linear finite element approximation, with n = 5
subintervals in the mesh,
to the solution
of
-lx
((x +
1)
~~)
=
1,
u(O)
=
2,
u(1) =
1.
The error shown
in
the bottom
graph
is
due
only to round-off
error-the
"approxi-
mation" is in fact
equal
to the exact solution.
Exercises
1. (a) Using direct integration, find the exact solution
to
the BVP from Exam-
ple 5.21.
(b) Repeat the calculations from Example 5.21, using
an
increasing sequence
of values of
n.
Produce graphs similar
to
Figure 5.16, or otherwise mea-
sure
the
errors in the approximation. Try to identify
the
size of
the
error
as a function of
h.
34
2.
(a) Compute the exact solution
to
the
BVP
from Example 5.22.
(b) Explain
why,
for this particular BVP,
the
finite element method computes
the
exact, rather
than
an
approximate, solution.
3.
Use piecewise linear finite elements
and
a regular mesh
to
solve
the
following
34To
perform
these
calculations for n
much
larger
than
5 will require
the
use
of
a
computer.
One could,
of
course,
write
a program, in a language such as
Fortran
or
C,
to
do
the
calculations.
However,
there
exist powerful interactive software
programs
that
integrate numerical calculations,
programming,
and
graphics,
and
these
are
much
more convenient
to
use. MATLAB is
particularly
suitable
for
the
finite element calculations needed for
this
book, since
it
is designed
to
facilitate
matrix
computations.
Mathematica
and
Maple
are
other
possibilities.

The
exact solution
is
The
results
of the
last exercise
will
be
required.
The
exact solution
is
5.6.
Piecewise
polynomials
and the
finite
element
method
201
problem:
Use
n =
10,20,40,...
elements,
and
determine (experimentally)
an
exponent
»
so
that
the
error
is
Here
error
is
defined
to be the
maximum absolute
difference
between
the
exact
and
approximate solutions. (Determine
the
exact solution
by
integration;
you
will
need
it to
compute
the
error
in the
approximations.)
4.
Repeat Exercise
3 for the BVP
6.
Repeat Exercise
3 for the BVP
where
k and p
satisfy
k(x)
> 0,
p(x]
> 0 for x
G
[0,^].
What
is the
bilinear
form
for
this BVP?
5.
Derive
the
weak
form
of the BVP
5.6. Piecewise polynomials
and
the finite element method
problem:
J2u
2
- dx
2
= X ,
U(O)
= 0,
u(1) =
O.
201
Use n =
10,20,40,
...
elements, and determine (experimentally) an exponent
p so
that
the error
is
o
(:p)
.
Here error
is
defined
to
be the maximum absolute difference between
the
exact
and approximate solutions. (Determine the exact solution by integration; you
will need it
to
compute the error in the approximations.)
4.
Repeat Exercise 3 for the BVP
d ( 2 dU)
- dx
(1
+ x ) dx =
1,
0 < x < 1,
u(O)
= 0,
u(1) =
O.
The exact solution
is
2ln2
1
u(x) =
-7r-
tan-
1
(x) -
2ln
(1
+ x
2
).
5.
Derive the weak form of
the
BVP
d ( dU)
- dx k(x) dx
+ p(x)u =
I(x),
0 < x <
f,
u(O)
= 0,
u(f) = 0,
where k and p satisfy k(x) > 0, p(x) > 0 for x E
[0,
fl.
What
is
the bilinear
form for this BVP?
6.
Repeat Exercise 3 for the BVP
J2u
1
--
+2u=
--x
dx
2
2'
u(O)
= 0,
u(1) =
O.
The results of the last exercise will be required. The exact solution is
u(x) = clev'2x + cze-v'2x +
~
-
~,

5.7
Green's
functions
for
BVPs
The
zero
function
is
always
a
solution
of a
linear homogeneous
differential
equation.
Suppose
we
have
a
BVP,
defined
by a
linear
differential
equation
and
Dirichlet
or
Neumann
boundary conditions, satisfying
the
existence
and
uniqueness property.
Then
the BVP has a
nonzero solution only
if the
differential
equation
is
inhomoge-
neous
or the
boundary conditions
are
inhomogeneous
(or
both).
We
will
focus
on
the
differential
equation, assuming
the
boundary
conditions
are
homogeneous,
and
present
a
formula
that
expresses
the
solution explicitly
in
terms
of the
right-hand
side
of the
differential
equation.
As
our first
example,
we
consider
the BVP
202
Chapter
5.
Boundary
value problems
in
statics
where
The
"data"
for
(5.61)
is the
forcing
function
/,
which
is a
function
of the
spatial
variable
x.
By two
integrations,
we can
determine
a
formula
for
u
in
terms
of /:
(To
verify
the
last
step,
the
reader should sketch
the
domain
of
integration
for the
double integral,
and
change
the
order
of
integration.)
We can
thus write
the
solution
as
202
Chapter
5.
Boundary value problems
in
statics
where
Cl
= - 4
(e-v'2
_ ev'2) ,
ev'2
+ 1
5.7 Green's functions for BVPs
The zero function
is
always a solution of a linear homogeneous differential equation.
Suppose
we
have a BVP, defined by a linear differential equation and Dirichlet or
Neumann boundary conditions, satisfying
the
existence and uniqueness property.
Then
the
BVP
has a nonzero solution only if
the
differential equation
is
inhomoge-
neous or
the
boundary conditions are inhomogeneous (or both).
We
will focus on
the
differential equation, assuming
the
boundary conditions are homogeneous, and
present a formula
that
expresses
the
solution explicitly in terms of
the
right-hand
side of
the
differential equation.
As our first example,
we
consider
the
BVP
d (
dU)
-
dx
k(x)
dx
=
f(x),
0 < x <
l,
u(O)
= 0,
(5.61)
du
dx(l)
=0.
The "data" for (5.61)
is
the forcing function f, which
is
a function of the spatial
variable
x. By two integrations,
we
can determine a formula for u in terms of f:
d (
du
)
-
dx
k(x)
dx
(x) =
f(x)
du
r
i
~
k(x)
dx
(x)
=
1x
fey)
dy
(since
~~(l)
=
0)
du
1
ri
~
dx
(x) = k(x)
1x
fey)
dy
r 1
rt
~
u(x) =
10
k(z)
1z
f(y)dydz
(since
u(O)
=
0)
r
i
{
rmin{x,y}
(
1)
}
~
u(x) =
10
10
k(z)
dz
fey)
dy.
(To verify
the
last step,
the
reader should sketch the domain of integration for
the
double integral, and change
the
order of integration.)
We
can thus write
the
solution
as
u(x) =
Io
i
g(x;y)f(y)dy,
(5.62)

5.7.
Green's
functions
for
BVPs
203
where
By
inspection
of
formula
(5.62),
we see
that,
for a
particular
x, the
value
u(x)
is
a
weighted
sum of the
data
/
over
the
interval
[0,£].
Indeed,
for a
given
x and
y,
g(x;y)
indicates
the
effect
on the
solution
u at x of the
data
/ at y. The
function
g
is
called
the
Green's
function
for BVP
(5.61).
To
expose
the
meaning
of the
Green's
function
more plainly,
we
consider
a
right-hand-side
function
/
that
is
concentrated
at a
single point
x =
£.
We
define
dAx
by
(see
Figure 5.18)
and let
f&
x
(x)
=
d^
x
(x
—
^).
The
solution
of
(5.61), with
/
=
/A
X)
is
Since
for
all Ax, we see
that
u(x)
is a
weighted average
of
g(x;
y)
(considered
as a
function
of
y)
over
the
interval
£
—
Ax
<
y
<
£
+
Ax.
As
Ax
—>•
0,
this weighted average
converges
to
<?(x;£).
We
now
interpret this result
in
terms
of a
specific
application.
We
consider
an
elastic
bar of
length
I
and
stiffness
k(x) hanging with
one end fixed at x = 0
and the
other
end (at x =
K)
free.
The
displacement
u of the bar is
modeled
by the
BVP
(5.61), where
/ is the
external
force
density
(in
units
of
force
per
volume).
The
quantity
is
the
total
force
exerted
on the
entire
bar. Since
and
/AX
is
zero except
on the
interval
[£
—
Ax,£+Ax],
we see
that
the
total
pressure
exerted
on the bar is A and it is
concentrated more
and
more
at x =
£
as Ax
->
0.
In
the
limit,
the
external
force
on the bar
consists
of a
pressure
of 1
unit acting
on
the
cross-section
of the bar at x =
£.
The
response
of the
bar,
in the
limit,
is
w(x)
=g(x]£).
5.7. Green's functions for BVPs
203
where
rmin{x,y}
( 1 )
g(x;y) =
Jo
k(z)
dz.
(5.63)
By inspection of formula (5.62),
we
see
that,
for a particular x,
the
value u(x)
is
a weighted sum of
the
data
f over the interval
[O,.€].
Indeed, for a given x and y,
g(x; y) indicates the effect on
the
solution u
at
x of
the
data
f
at
y.
The function
9
is
called the Green's function for BVP (5.61).
To
expose the meaning of the Green's function more plainly,
we
consider a
right-hand-side function
f
that
is
concentrated
at
a single point x
=~.
We
define
d
Ax
by
{
x+Ax
AX2 ,
dA
(x) =
_x-Ax
u-X
AX2 ,
0,
-Llx
< x < 0,
0<
x < Llx,
otherwise
(see Figure
5.18) and let
fAx(x)
=
dAx(X-~).
The solution of (5.61), with f = fAx,
is
Since
l
{+AX
d
Ax
(y -
~)
dy = 1
{-Ax
for all Llx,
we
see
that
u(x)
is
a weighted average of g(x;
y)
(considered as a function
of
y)
over the interval
~
- Llx
::;
y
::;
~
+ Llx. As Llx
-+
0, this weighted average
converges
to
g(x;~).
We
now interpret this result in terms of a specific application.
We
consider
an elastic
bar
of length £ and stiffness k(x) hanging with one end fixed
at
x = 0
and the other end
(at
x =
£)
free. The displacement u of
the
bar is modeled by the
BVP
(5.61), where f
is
the external force density (in units of force per volume).
The quantity
fot
Ahx
(y)
dy
is the total force exerted on the entire bar. Since
fot
hx(Y)
dy
= 1 for all Llx > 0
and
fAx
is
zero except on the interval
[~-
Llx,
~
+ Llx],
we
see
that
the
total
pressure
exerted on
the
bar
is
A and
it
is
concentrated more and more
at
x =
~
as Llx
-+
O.
In the limit,
the
external force on the
bar
consists of a pressure of 1 unit acting
on
the
cross-section of
the
bar
at
x
=~.
The response of the bar, in
the
limit,
is
u(x) = g(x;
~).

204
Chapter
5.
Boundary value problems
in
statics
Figure
5.18.
The
function
d&
x
(Ax =
O.I).
Thus
we see
that,
for a fixed
£,
g(x;
£)
is a
solution
to
(5.61)
for a
special right-
hand
side—a
forcing
function
of
magnitude
1
concentrated
at x =
£.
However,
this
forcing
function
is not a
true function
in the
usual sense. Indeed,
the
function
d^\
x
has the
following
properties:
is
a
weighted average
of g on the
interval
[—Ax,
Ax].
Since
the
limit,
as
Ax
—>•
0, of the
weighted average
of g
over
[—Ax,
Ax] is
#(0)
when
g is
continuous, these properties suggest
that
we
define
the
limit
6 of
d<\
x
as
Ax
—>•
0 by the
following
properties:
204
Chapter
5.
Boundary value problems
in
statics
10~------~-------r------~------~
9
8
7
6
5
4
3
2
O~------~-----L~~----~------~
-1
-0.5 0
0.5
x
Figure
5.18.
The function
d/:;.x
(!lx
= 0.1).
Thus
we see
that,
for a fixed
~,
g(x;~)
is
a solution
to
(5.61) for a special right-
hand
side-a
forcing function of
magnitude
1
concentrated
at
x =
~.
However,
this
forcing function
is
not
a
true
function
in
the
usual sense. Indeed,
the
function
d/:;.x
has
the
following properties:
•
d~x(x)
= 0, x
ft
[-!lx,
!lx].
•
I:
d/:;.x(x)
dx =
I~~x
d/:;.x(x)
dx = 1 for all
!lx
> 0, provided
[-!lx,
!lx] c
[a,
b],
and
I:
d/:;.x(x)
dx = 0
if
!lx
::;
a
or
-!lx
2:
b.
•
If
9 is a continuous function,
and
[-!lx,
!lx] c
[a,
b],
then
is a weighted average of 9 on
the
interval
[-!lx,
!lx].
Since
the
limit, as
!lx
~
0,
of
the
weighted average
of
9 over
[-!lx,
!lx) is
g(O)
when 9
is
continuous,
these
properties suggest
that
we define
the
limit 8
of
d/:;.x
as
!lx
~
0
by
the
following properties:
• 8(x) = 0 if x #
O.
• 8(0) =
00.
•
J:
8(x)dx
= 1 if 0 E
[a,b],
and
I:
8(x)dx
= 0 if 0
rf-
[a,
b).

Since
6 is not a
function,
but a
generalized
function,
we
regard
the
last
two
properties
as
assumptions.
From
this discussion,
we see
that
the
Green's function
g for
(5.61)
has the
property
that
u(x)
=
g(x;
£)
is the
solution
of the BVP
If
g is a
continuous
function
and
The
"function"
8 is not a
function
at
all—any
ordinary
function
d has the
property
that
if d is
nonzero only
at a
single
point
on an
interval,
then
the
integral
of d
over
that
interval
is
zero. However,
it is
useful
to
regard
8 as a
generalized
function.
The
particular generalized
function
8 is
called
the
Dirac
delta
function
(or
simply
the
delta
function)
and is
defined
by the
siftinq
property:
If
g is a
continuous
function
and 0
e
[0,6],
then
J
a
8(x)g(x}dx
=
c/(0).
If 0
<£
[a,
6],
then
fc
S(x}g(x)
dx = 0.
By
a
simple change
of
variables,
we see
that
the
following
property also holds:
Since
S is
formally
an
even function
(8(—x)
=
8(x)),
we
also have
We
can
verify
this result using physical reasoning; this
is
particularly simple
in
the
case
of a
homogeneous bar.
We
consider
the
following
thought experiment:
We
apply
a
unit pressure
(in the
positive direction)
to the
cross-section
at x =
£
6
(0,^).
(It is not
obvious
how
such
a
pressure could actually
be
applied
in a
physical
experiment, which
is why we
term this
a
"thought
experiment.")
Since
the bar is
fixed at x = 0, and the end at x
—
t
is
free,
it is not
hard
to see
what
the
resulting
displacement
will
be. The
part
of the bar
originally between
x = 0 and x —
£
will
stretch
from
its
original length
of
£
to a
length
of £ +
A£,
where
(the pressure,
1, is
proportional
to the
relative change
in
length
(A£/£)).
Therefore,
A£,
which
is the
displacement
u(£),
is
£/fc.
Since
the bar is
homogeneous,
the
displacement
in the
Dart
of the bar
above
x = £ is
If
g is a
continuous function
and £ G [a,
6],
then
J
8(x)g(x
—
£}
dx =
0(0-
5.7.
Green's
functions
for
BVPs
205
If
g is a
continuous function
and £
e
[a, 6],
then
J
8(x)g(£
—
x}dx
=
0(0.
5.7.
Green's
functions for BVPs
205
•
If
9 is a continuous function
and
0 E
[a,
b],
then
J:
8(x)g(x)
dx
=
g(O).
If
o
(j
[a,
b],
then
J:
8(x)g(x)
dx
=
o.
The
"function" 8
is
not
a function
at
all-any
ordinary function d has the property
that
if d
is
nonzero only
at
a single point on
an
interval, then
the
integral of
dover
that
interval is zero. However,
it
is useful
to
regard 8 as a generalized function.
The
particular generalized function 8
is
called
the
Dirac delta
junction
(or simply the
delta
function)
and
is defined by
the
sifting property:
If
9 is a continuous function
and
0 E
[a,
b],
then
J:
8(x)g(x)
dx
=
g(O).
If
0 (j
[a,
bj,
then
J:
8(x)g(x)
dx
=
O.
By a simple change of variables,
we
see
that
the
following property also holds:
If
9 is a continuous function and
~
E
[a,
b],
then
J:
8(x)g(x
-~)
dx
=
g(~).
Since 8 is formally
an
even function (8(
-x)
= 8(x)),
we
also have
If
9 is a continuous function and
~
E
[a,
b],
then
J:
8(x)g(~
-
x)
dx
=
g(~).
Since 8 is not a function,
but
a generalized function,
we
regard
the
last two properties
as assumptions.
From this discussion,
we
see
that
the
Green's function 9 for (5.61) has
the
property
that
u(x) =
g(x;~)
is
the
solution of
the
BVP
-! (k(X)
~~)
= 8(x -
~),
0 < x <
£,
u(O)
=
0,
dUe£)
=0.
dx
(5.64)
We
can verify this result using physical reasoning; this is particularly simple
in
the
case of a homogeneous bar.
We
consider
the
following thought experiment:
We
apply a unit pressure (in the positive direction)
to
the
cross-section
at
x =
~
E
(0, e). (It is not obvious how such a pressure could actually be applied in a physical
experiment, which
is
why
we
term
this a "thought experiment.") Since
the
bar
is
fixed
at
x =
0,
and
the
end
at
x = £
is
free,
it
is
not
hard
to
see
what
the
resulting
displacement will be.
The
part
of
the
bar
originally between x = 0
and
x =
~
will
stretch from its original length of
~
to
a length of
~
+
~~,
where
k~~
= 1
~
(the pressure,
1,
is proportional
to
the
relative change in length
(~~/~)).
Therefore,
~~,
which is
the
displacement
u(~),
is
~/k.
Since
the
bar
is
homogeneous,
the
displacement in
the
part
of the
bar
above x =
~
is
x
u(x) = k' 0
~
x
~
~.
206
Chapter
5.
Boundary value problems
in
statics
What
about
the
part
of the bar
originally between
x =
£
and x =
11
This
part
of
the bar is not
stretched
at
all;
it
merely moves because
of the
displacement
in the
part
of the bar
above
it. We
therefore
obtain
Combining these
two
formulas gives
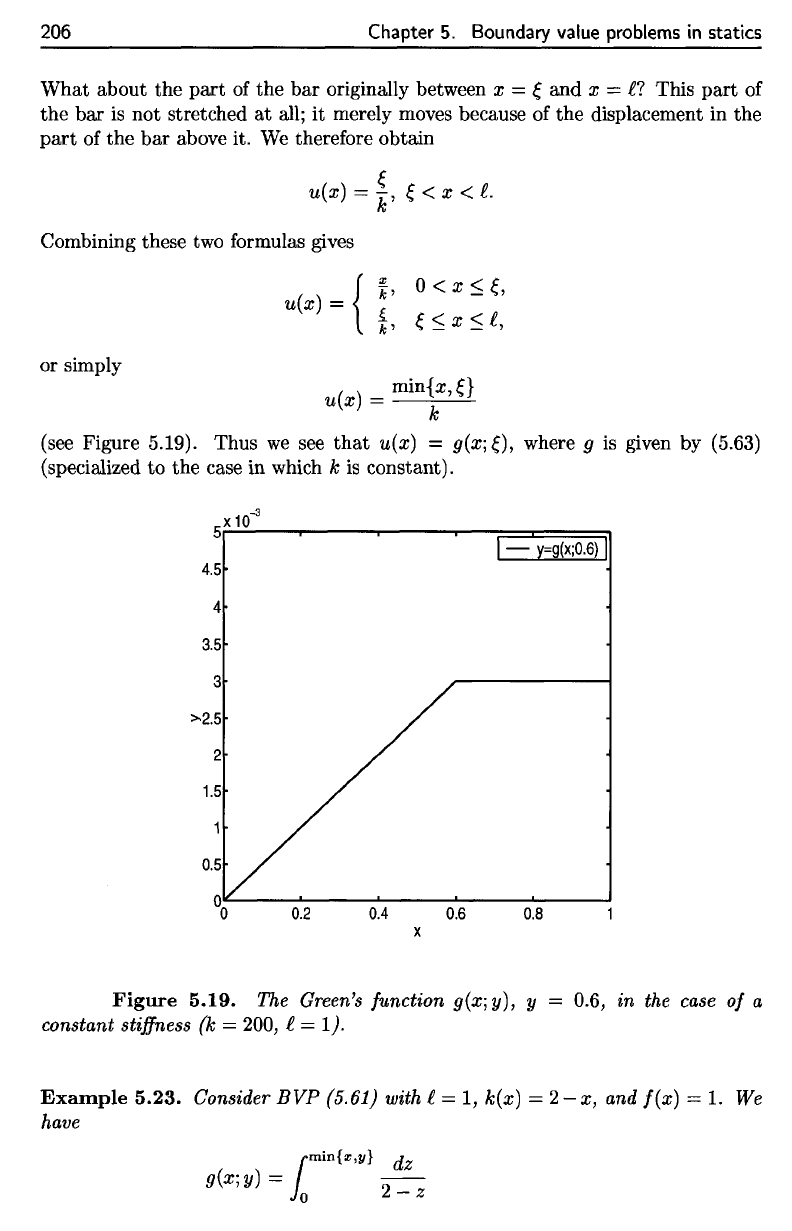
(see Figure 5.19). Thus
we see
that
u(x)
=
g(x;£),
where
g is
given
by
(5.63)
(specialized
to the
case
in
which
k is
constant).
Figure
5.19.
The
Green's
function
g(x;y],
y =
0.6,
in the
case
of a
constant
stiffness
(k =
200,
t =
I).
Example
5.23. Consider
BVP
(5.61) with
1=1,
k(x)
=
1-x,
and
f(x)
= 1. We
have
or
simply
206
Chapter
5.
Boundary value problems in statics
What
about the
part
of the
bar
originally between x =
~
and x =
l?
This
part
of
the
bar
is
not stretched
at
all;
it
merely moves because of the displacement in the
part
of
the
bar
above it.
We
therefore obtain
Combining these two formulas gives
or simply
u(x) = {
~'
k'
u(x) =
min{x,~}
k
(see Figure 5.19). Thus
we
see
that
u(x)
= g(x;
~),
where 9
is
given by (5.63)
(specialized
to
the
case in which k
is
constant).
-
=g(x;O.6)
4.5
4
3.5
0.8
x
Figure
5.19.
The Green's function g(x; y), y = 0.6,
in
the case
of
a
constant stiffness (k
= 200, £ = 1).
Example
5.23.
Consider
BVP
(5.61) with £ = 1,
k(x)
= 2 -
x,
and
f(x)
= 1. We
have
l
ffiin
{X,Y}
dz
g(x;y)
= -
o
2-z

Our
results above show
that,
for
each
/ €
C[0,£],
there
is a
unique solution
to
Ku
=
f.
In
other
words,
K is an
invertible
operator.
Moreover,
the
solution
to
Ku
= f is u =
Mf,
where
M
:
C[0,l]
->
C^[0,£]
is
denned
by
Exercises
1.
Use the
Green's
function
to
solve (5.61) when
t = 1,
/(#)
= 1, and
k(x)
=
e
x
.
2.
Prove directly
(by
substituting
u
into
the
differential
equation
and
boundary
conditions)
that
the
function
u
defined
by
(5.62)
and
(5.63) solves (5.61).
5.7.
Green's
functions
for
BVPs
207
Therefore,
5.7.1
The
Green's
function
and the
inverse
of a
differential
operator
We
write
Therefore,
KM
f
=
/,
which shows
that
M = K
x
,
the
inverse operator
of
K.
It
follows
that
must also hold. Thus
the
Green's
function
defines
the
inverse
of the
differential
operator.
5.7.
Green's
functions for BVPs
Therefore,
=
-log
(2
_
z)l~in{x,y}
= log 2
-log
(2
- min{x, y})
_
{IOg2-10
g
(2-
y
),
O<y<x,
- log 2 - log
(2
- x), x < y <
1.
u(x) =
fo1
g(x;
y)
dy
(since fey) = 1)
=
fox
{log 2
-log
(2
-
v)}
dy
+
11
{log 2
-log
(2
-
x)}
dy
207
= x(1 + log
2)
+
(2
- x) log
(2
- x) - log 4 +
(1
- x) (log 2 - log
(2
- x))
= x + log (1 -
~).
5.7.1
The
Green's function and the inverse
of
a differential
operator
We
write
C![O,i] = {u E C
2
[O,i]
u(O)
=
~~(i)
=
o}
and
K : c;'
[0,
i]
-+
C[O,
i] by
Ku
=
--
k(x)-
.
d (
dU)
dx dx
Our
results above show
that,
for each f E
C[O,
i], there is a unique solution
to
Ku
=
f.
In
other
words, K
is
an invertible operator. Moreover,
the
solution
to
Ku
= f is u =
Mf,
where
M:
C[O,i]-+ C;'[O,i] is defined by
(Mf)(x)
=
1£
g(x;y)f(y)
dy.
Therefore, K M f =
f,
which shows
that
M =
K-
1
,
the
inverse operator of
K.
It
follows
that
MKu
= u for all u E C